一种基于SDG和数据重构的故障诊断方法

王 毓 杨煜普 屈卫东

(上海交通大学电子信息与电气工程学院自动化系，上海 200240)

随着工业过程控制系统不断朝着大规模、智能化和复杂化的方向发展，安全问题日益成为大家关心的主要问题之一。在过去的几十年中，故障诊断方法的研究得到了国内外学者的广泛关注。这些方法从整体上可以分为定性方法和定量分析两大类[1]。其中，在定量分析方法中，基于多元统计的方法是近年来关注较多的方法。传统的基于贡献图的统计方法是最受欢迎的方法之一，那些具有较大贡献值的变量被认为是引起故障的变量。Kourti T和MacGregor J F将贡献图法应用到高压低密度的聚乙烯反应过程中[2]，他们认为贡献图可能不能确定导致故障的原因变量。Westerhuis J A等引入了贡献图的置信限来增强鉴别偏离正常运行条件的原因变量的能力[3]。他们认为在应用贡献图法时必须谨慎小心，因为PCA的残差能将某个变量的贡献值转移到其他变量的贡献值上。最近，Alcala C F和Qin S J提出了基于重构的贡献图方法(RBC)[4]，该方法保证了故障变量有最大的贡献值，从而比传统的贡献图法要有更精确的鉴别能力。但是，RBC仍没有解决贡献值从一个变量转移到其他变量的问题。基于贡献图的多元统计方法的主要缺点是没有考虑到故障在系统中的传播，导致故障变量定位错误而不能检测出引起故障的根本原因。笔者将SDG和数据重构相结合，在故障发生时在SDG所有有效节点和相容路径方向上对测试样本进行重构，其中重构指标最大的方向被认为是实际故障的传播方向，而传播方向上的起始节点被认为是引起故障的根本原因变量。

1 主元分析与数据重构方法①

1.1 主元分析

笔者讨论的故障诊断与隔离方法利用正常的过程模型，通过PCA将样本向量分解为两个部分：

(1)

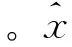
(2)

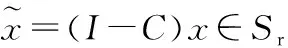
(3)

且dim(Sr)=m-k。

1.2 数据重构方法

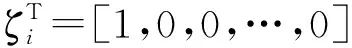
为了在所有可能的故障中检测出故障Ψi，必须在所有可能的故障方向ζj上来进行重构，重构方法是：对于每个假设的故障Ψj，测量的样本向量x在方向ζj上移动，直到它离主元空间Sp的距离最短。图1显示了通过重构进行故障辨识的几何解释。在图中，假设故障Ψj发生了，通过将x沿着ζj方向移动得到xj。即：xj=x-fjζj。其中fj是对f的估计，表示沿着方向ζj朝主元超平面移动的位移大小。xj表示沿方向ζj重构后的样本向量。如果假设的故障Ψj就是实际发生的故障Ψi，那么重构后的样本向量xj应该最接近x*。

图1 重构方法的几何解释

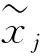
于是，故障隔离的问题就转化为以下求极值的问题：

(4)

(5)

(6)

式(6)是使得重构后样本向量的SPE最大程度减小的充要条件。因此：

(7)

(8)

它描述的是数据样本沿ζj方向重构后样本SPE的下降的程度，其取值范围为[0，1]，取值越大，表示Ψj越有可能是真实的故障Ψi。

以上分析是基于故障Ψi是由于某个变量引起的这个前提下进行的，而实际情况并没有如此简单。通常情况下，故障会随着系统部件进行传播，往往其统计值变化最明显的变量只是故障导致的结果，而非引起故障的原因。按照文献[5]的观点，必须在所有可能的方向上对xj其进行重构，但如果单纯地搜索所有可能的方向，搜索空间将随着变量的增加呈指数增长，当变量过多时，搜索空间由于过大导致故障诊断很难进行下去。因此，必须充分利用系统的结构特性，有目的地对故障数据进行重构。笔者将利用符号有向图来对故障可能的传播方向进行确定，从而避免搜索空间爆炸的问题。

2 基于SDG和数据重构的故障诊断

2.1 监控统计量及SDG有效节点的确定

笔者采用的数据重构标准是使重构后的样本点离主元距离最小，即使重构后的样本SPE最小，因此，检测故障时采用SPE统计量和相应的控制线[4]。

CUSUM是检测微小变化的有效工具，尤其对于监控变化量为0.5～2.0个标准差的样本效果较好。为了避免设定每个变量上、下限这些繁冗的工作，笔者采用CUSUM监控量和V-mask方法来确定有效节点。V-mask的主要参数为：

(9)

(10)

h=d·k

(11)

式中d——最近的采样点离V定点的距离；

h——最近的采样点离V的上下臂的距离；

k——V的斜率；

α——误报率；

β——漏报率；

δ——能检测到的偏移量(样本标准差的倍数)；

σx——样本的标准差。

2.2 故障诊断

整个故障诊断的步骤为：首先通过采集正常数据进行离线训练，即通过PCA对预处理后的数据进行分解，进而求出SPE的控制线。根据系统流图，建立SDG模型，在设定漏报率、误报率、检测偏移量后确定各变量V-mask的参数。然后实时采集系统未知状态的工作数据，对各变量的CUSUM和样本SPE进行监控，如果SPE超过了控制线，表示系统发生了故障，之后通过CUSUM统计量确定有效节点，通过搜索所有可能的相容路径，在所有有效节点和相容路径方向上对测试数据进行重构，其指标η2最大的方向，便是真实的故障传播方向，该方向上的起始节点被认为是故障的原因变量，而导致该节点异常的事件被认为是产生故障的根本原因。

3 TE实验平台的故障案例分析

TE实验平台是Downs J J和Vogel E F根据Eastman化学公司的世界工艺流程作了少许修改后于1993年提出的[6]，以下以故障IDV(1)为例加以分析。

首先通过PCA对预处理后的正常样本数据进行分解，正常数据包括480个样本点，每个样本点是52维的向量。这里主元个数按照特征值累计贡献率来选取，一般要求90%以上，但也不能太大，选择太大将使检测过程容易受噪声影响，笔者按96%选取。为了确定各变量V-mask参数，设定误报率为0.3%，漏报率为1%，检测偏移量为各变量标准差的0.5倍。然后对测试数据进行检测。这里，测试数据为960个样本点，每个样本点是52维的向量，其中，故障IDV(1)从第161个样本点开始引入。通过对各变量的CUSUM和样本SPE进行监控，确定故障发生与否，同时通过对有效节点的确定，找出使η2最大的相容路径。

需要注意的是，由于通过V-mask确定CUSUM是否超过控制线具有延时性，笔者设定为10个采样周期。

图2显示了SPE随样本序列的变化，其中虚线为控制线，超过控制线表示故障发生。从图中可以看出，故障在第160个样本附近被检测到。仿真实验在163个样本点检测到故障发生，故障发生时，有向图中的有效节点及其含义见表1，系统有向图和节点含义见参考文献[7]。

图2 SPE随样本序列的变化

序号节点节点含义1MV1D进料阀门(流2)2MV2E进料阀门(流3)3MV3A进料阀门(流1)4MV5压缩机阀门5MV6排空物料阀门(流9)6MV10反应器冷却水控制阀门7P7反应器压力8P13气液分离器压力9P16解吸塔压力10T21反应器冷却水出口温度11XA反应器给料组分A(流6)12XC反应器给料组分C(流6)

为了在所有可能的方向上对样本进行重构，对所有有效节点从1～12进行编号(表1)。考虑到故障的传播，需在有向图的相容路径方向上进行重构，搜索得到的3条相容路径为：XA↓⟹MV3↑、MV10↓⟹T21↑、XC↑⟹P7↑⟹P13↑⟹P16↑，分别编号为13、14、15。

图3所示为测试样本在所有15个方向上重构后的故障指标，从图中可以看出，编号为15的相容路径指标最大，可以判断出该相容路径为故障传播路径，即反应器给料组分C的增加，导致反应器压力、气液分离器压力和解析塔的压力增加。所有故障中只有故障1含有组分C的变化，由此可以推断该故障为故障1。作为对比，图4显示了传统贡献图法各变量的贡献值，其中反应器温度贡献值最大，此时不能推断是故障1还是其他故障导致反应器温度增加。由此可以看出，通过SDG和数据重构的方法对检测故障发生的根本原因更加有效。

图3 所有重构方向的隔离指标

图4 故障1发生时所有变量的贡献

4 结束语

介绍了一种基于SDG和数据重构的故障诊断方法。该方法先用PCA模型的SPE指标检测出异常的发生，然后通过各变量的CUSUM对SDG的有效节点进行确定，当SPE超过控制线时，通过在所有有效节点和相容路径方向上对测量样本进行重构，重构后SPE下降最多或故障隔离指标最大时，表示该方向为故障的传播方向。通过在TEP模型上的仿真表明，该方法比传统贡献图法对检测故障的根本原因更加有效。