时滞系统的双自由度Smith模糊PID控制器设计与仿真

孙立强 郑恩让

(陕西科技大学电气与信息工程学院，西安 710021)

模糊PID控制器是传统的PID控制与模糊控制相结合形成的一种智能控制器，它融合了PID控制器不依赖对象数学模型及模糊控制器良好的知识表达能力等优点[1]，合理地设置控制器的参数能够对大时滞过程取得理想的控制效果。

笔者研究的模糊PID控制器改进了文献[2]中模糊PID的控制结构，避免了参数的耦合；给定输入端增加的比例和微分部分的自由度，可以有效减小系统动态响应的最大超调量[3]，减小扰动对系统的影响。仿真结果表明，笔者设计的控制器改善了输入跟踪响应和扰动响应特性曲线，并对模糊PID控制器的鲁棒性进行了验证。

1 模糊PID控制器①

1.1 模糊PID的控制结构

(1)

KFP=Ku(β1PKe+β2DKd)

(2)

KFI=β2PKeKu

(3)

KFD=β1DKdKu

(4)

式中KFD——模糊PID的微分增益；

KFI——模糊PID的积分增益；

KFP——模糊PID的比例增益；

β1、β2——比例和积分的组合系数。

由式(2)～(4)可以看出，模糊PID控制的3个参数和β1、β2都有关系，且存在耦合作用。

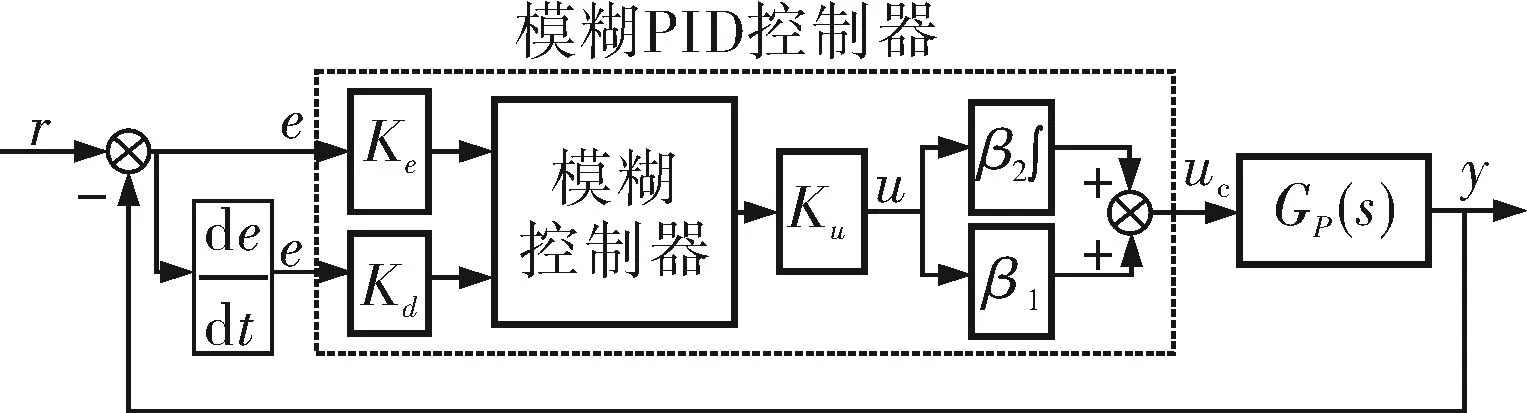
图1 模糊PID控制框图

1.2 改进型模糊PID控制器

为了解决上述模糊PID控制器的参数耦合问题，提出如图2所示的控制结构，该模糊控制器是在模糊控制器的基础上构造出一个积分作用与模糊控制器迭加共同构成PID控制器。此外，图2还是一个多自由度的模糊PID控制器，在输入端加入调节参数α1、α2和α3，则：

(5)

图2 多自由度改进型模糊PID控制结构

通常取α3=1，模糊PID控制变为双自由度模糊PID控制器，通过调整α1和α2调节给定的强度，可以有效地减小动态响应的最大超调量。假设系统的主导极点为σ+jω，参数的计算式为[4]：

(6)

输入调节参数可以进一步等效为一个输入滤波器F(s)/C(s)，可以有效地简化控制器的结构(图3)[5]。输入滤波器的计算公式为：

(7)

图3 简化等效后的系统框图

(8)

系统的控制框图如图4所示。

图4 系统控制框图

1.3 模糊控制器设计

模糊控制器采用Mamdani推理算法，相关的推理运算法为：蕴含关系→求积、综合算法→取大、清晰化→面积中心法[6]。

控制器参数整定步骤为：

a. 令α1、α2和Ku均为1，Kd=0，调整Ke、TI使系统单位阶跃响应曲线收敛振荡；

b. 调节Kd和Ku值，调整微分和控制器输出强度，优化系统动态响应；

c. 调整α1、α2，进一步减小系统的动态超调量和调节时间；

d. 将输入调节参数等效为输入滤波器，简化控制器结构。

2 仿真研究

系统仿真对象选为一阶惯性加纯延迟环节：

(9)

模糊PID控制器的参数Ke=0.27、Kd=0.25、Ku=1.5。

为验证输入调节参数α1、α2的控制效果，分别在t为0、40s时输入单位阶跃信号和d=0.2干扰信号，对比未加输入调节参数控制器和双自由度模糊PID控制器的系统动态响应曲线(图5)。

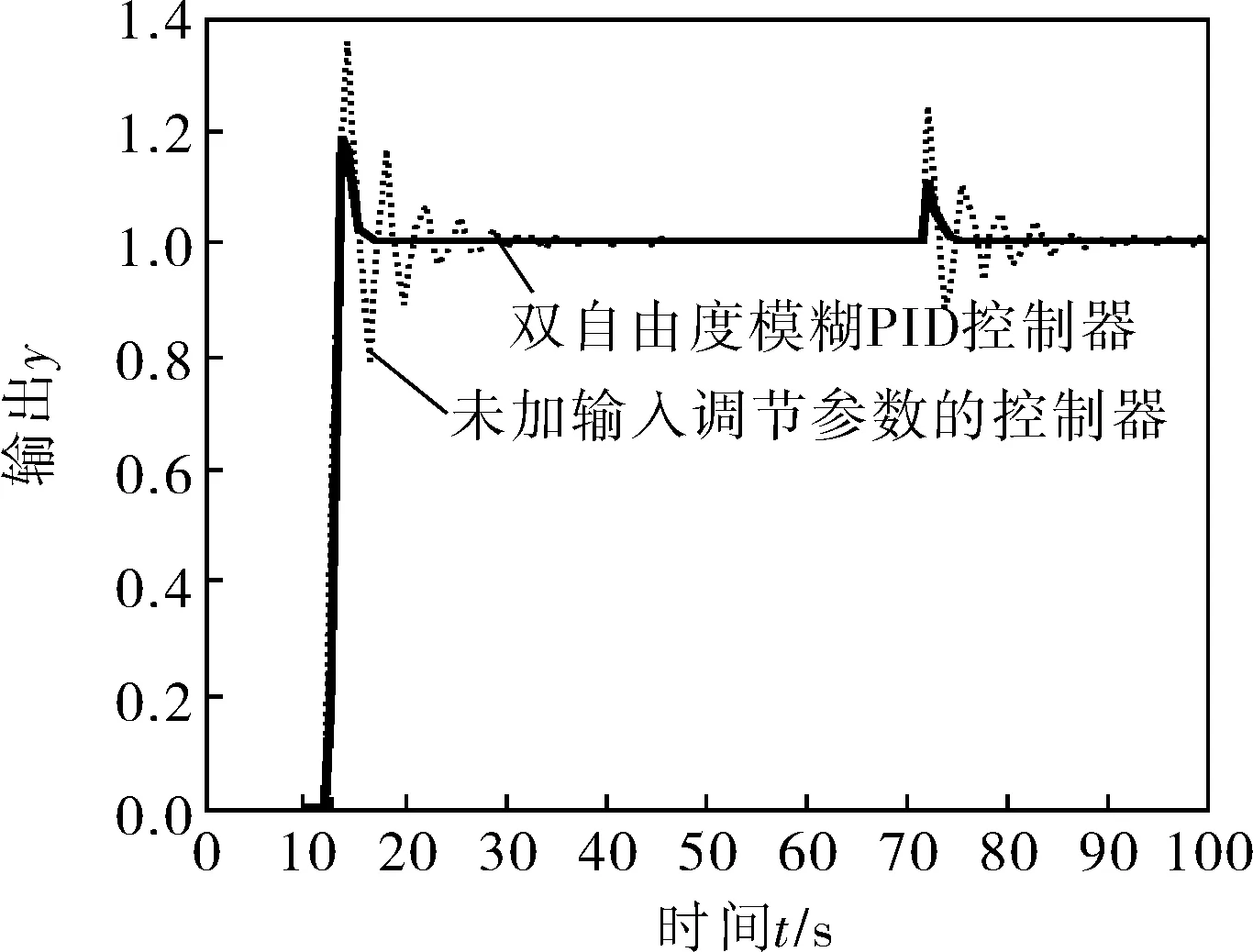
图5 双自由度控制器的动态响应曲线

验证改进型双自由度模糊PID控制器的鲁棒性，解决实际应用中很难建立精确的对象数学模型的问题，将对象数学模型的K、T、τ分别增加和减小20%[7]，得到的响应曲线如图6～8所示。

图6 模型参数K变化时的响应曲线

图7 模型参数T变化时的响应曲线

图8 模型参数τ变化时的响应曲线

由图5～8可知，未加入输入调节参数控制器的动态响应的最大超调量为40%，双自由度控制器的最大超调量为15%，可见双自由度控制器可以明显减小系统的最大超调量；加入干扰后双自由度控制器能够明显提高系统抗干扰能力，模型失配时，改进型双自由度模糊PID控制器的鲁棒性优于原控制器。

3 结束语

模糊PID控制器增加双自由自由度给定调节参数后，减小了系统的最大超调量，系统能够快速达到稳态，提高抗干扰能力。此外，分析解决了控制器参数耦合问题，降低了系统的参数整定的难度，整定出的模糊PID参数具有良好的鲁棒性。