改进多智能体蚁群算法在电力系统无功优化中的应用

姚建红 张玲玉 孙大兴

(东北石油大学，黑龙江 大庆 163318)

电力系统无功优化在电能质量、网络损耗和电压稳定性上有着决定性的作用，但目前还没有一种在计算时间、运算量及收敛性等方面兼具良好效果的优化算法。人工智能方法在电力系统无功优化上应用比较广泛，但仍有不足之处，对于常规蚁群算法而言主要体现在[1]：没有坚实的数学基础，也没有成型的系统分析方法，计算复杂[2]，易陷入局部最优及收敛速度慢[3]等。对于常规蚁群算法的缺陷，笔者利用多智能体系统与改进的蚁群算法相结合，优势互补，克服了易陷入局部最优解和收敛速度受限的不足，从而实现较快、较精准的无功优化。

1 无功优化的数学模型①

无功优化的数学模型由目标函数、约束条件构成，其中约束条件包括等式约束条件和不等式约束条件。

以配电网电能损耗最小为目标函数：

(1)

选取潮流方程作为等式约束条件：

(2)

式中Bij、Gij——分别表示系统节点导纳矩阵中第i行第j列元素的虚部、实部；

gij——支路i-j电导；

n——系统总支路数；

Pi、Qi——分别为节点i的有功、无功功率；

Ui、Uj——节点i、j的电压幅值；

δi、δj——节点i、j的相角；

δij——节点i、j的相角差。

选取发电机无功出力、无功补偿装置的无功补偿容量和有载调压变压器的变比作控制变量，负荷节点电压作状态变量。控制变量不等式约束条件为：

(3)

状态变量不等式约束条件：

Uimin≤Ui≤Uimax

(4)

式中QCi——第i个无功补偿装置的无功补偿容量；

QCimax——第i个无功补偿装置的无功补偿容量上限；

QCimin——第i个无功补偿装置的无功补偿容量下限；

QGi——节点i发电机无功出力；

QGimax——节点i发电机无功出力上限；

QGimin——节点i发电机无功出力下限；

Ti——第i台有载调压变压器变比；

Timax——第i台有载调压变压器变比可调节的上限；

Timin——第i台有载调压变压器变比可调节的下限；

Ui——节点i的电压幅值；

Uimax——节点i电压幅值的上限；

Uimin——节点i电压幅值的下限。

2 多智能体蚁群算法

2.1 改进的蚁群算法

在数学领域中的旅行商问题中，有学者将遗传算法中的排序概念扩展到蚁群算法中[4]，改进后的算法得到了较好的收敛速度。进而，在此基础上对蚁群算法的权系数改进，并应用在电力系统无功优化领域中，以解决收敛速度慢等问题。

改进蚁群算法的思想：把蚂蚁寻优的一次循环结束后生成的路径按照长短排序，每只蚂蚁对更新信息素的贡献取决于生成路径的长短，路径越短贡献越大。改进权系数λk(1-N/Nmax)，对于全局信息素更新来说，所有蚂蚁都有相应的贡献。不仅在寻优过程中，提高对较优蚂蚁的重视程度，也降低对较差蚂蚁的忽略程度。因此，该算法是一种较好的改进算法。

在改进的算法中，搜索路径上的信息素按照下式对全局信息素更新：

τij(t+1)=ρ×τij(t)+Δτij

(5)

(6)

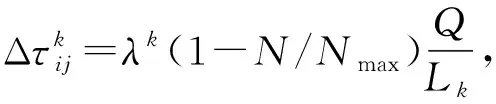
式中k——最优蚂蚁编号；

Lk——第k只最优蚂蚁搜索的路径长度；

λ——常数(0<λ<1)；

N——当前迭代次数；

Nmax——最大迭代次数；

对改进蚁群算法与一般蚁群算法进行验证，在初始参数设置相同的前提下，对比结果如图1表示。

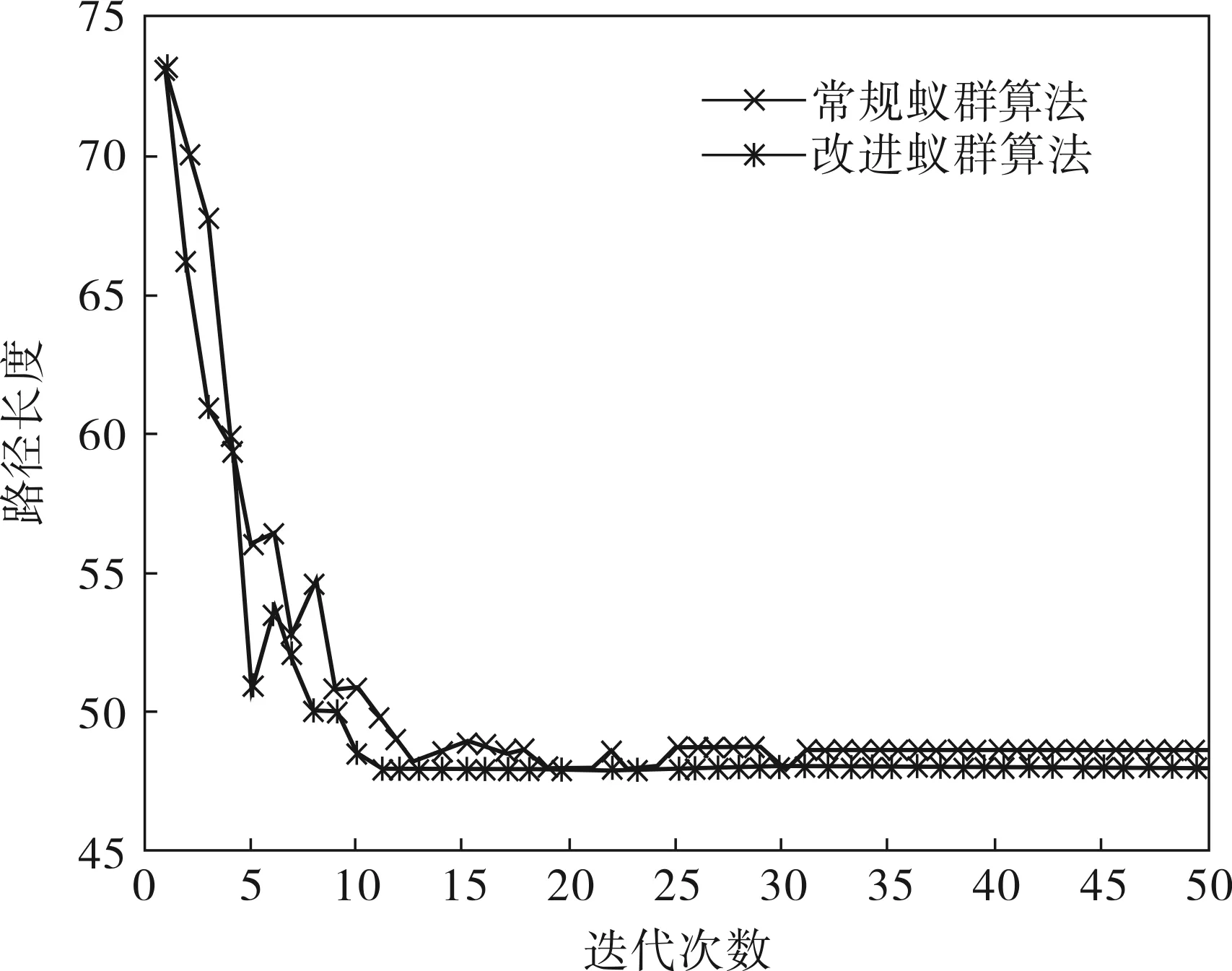
图1 改进蚁群算法与常规蚁群算法对比

由图1可知：改进蚁群算法和常规蚁群算法分别在迭代11次左右和13次左右得到全局最优解；改进的蚁群算法在搜索全局最优解收敛的过程较平稳，而常规蚁群算法在31代收敛，却陷入局部最优解。由此可知，基于排序加权的蚁群算法，在收敛速度上有明显的提高，有较好的实用性。

2.2 多智能体蚁群算法

多智能体系统，即Multi-Agent System，简称MAS，多个智能体(Agent)相互协作可以完成更复杂问题的求解，MAS将各种不同功能的Agent模块通过通信和协作结合起来，共同协调来完成任务，具有更大的灵活性和适应性[5]。

多智能体蚁群算法(Multi-Agent Ant Colony Optimization，简称MACO)是将改进的ACO和MAS的主要特征结合的一种优化算法。该改进的算法主要思想是任意一个Agent相当于改进蚁群算法中种群的一只蚂蚁，都有一个被优化问题决定的最佳适应值。Agent的目的就是在满足运行条件的限制下，尽可能减小其适应值。每个Agent不但可以和其邻居竞争与合作操作、自学习操作，还结合蚁群的搜索机制，与全局最优的智能体进行信息共享，并根据自身经验总结来修正智能体的行动策略，能够更快、更准确的收敛到全局最优解。

2.3 MACO算法的优化步骤

笔者改进算法的具体优化步骤如下：

a. 设置初始参数、约束条件的上/下限值、算法中需指定的控制参数和最大迭代次数；

b. 创建MAS中Agent“生存”的“格子”环境，产生初始的Agent，初始迭代次数为0；

c. 利用牛顿拉弗逊方法进行潮流计算，对每个Agent的适应值进行评估；

d. 每个Agent与其邻居竞争与合作，操作完成后，更新一次整个环境中的Agent；

e. 在MAS中，执行排序加权蚁群算法，进一步更新每个Agent在解空间的位置；

f. 重新对Agent的适应值进行评估；

g. 搜索最优适应值的Agent，再根据Agent的自学习操作，对Agent在解空间的位置再一次更新；

h. 迭代次数自加1；

i. 判断是否达到终止条件，即最大迭代次数或者满足收敛条件，若不满足，跳转到步骤c，若满足，则迭代终止，输出优化的最优解。

3 算例分析

将改进的算法应用于IEEE30节点系统进行算例分析，验证算法的有效性和可行性。系统中基准功率SB=100MVA，有6台发电机，38条支路，4台变压器，9台并联电容器和21个负荷节点，系统总负荷Ptotal=2.834，Qtotal=1.262。系统中参数设置见表1、2。

表1 发电机参数

表2 变压器变比参数

在初始条件下，通过潮流计算，得到ΣPG=2.869 1，ΣQG=1.380 7，网损Ploss约为0.035。初始参数为：总环境大小S=10(种群规模ant=100)，最大迭代次数Nmax=50，信息素启发因子α=1，自启发因子β=2，挥发系数ρ=0.1，加权系数λ=0.3，自学习环境大小s=4，自学习搜索半径sR=0.4；运行后，与遗传算法进行比较，表3显示出在条件相同的前提下，优化算法的对比结果。

表3 优化结果对比表

由表3可得到：多智能体蚁群算法对电网系统优化后，网络损耗为0.017，与遗传算法相比，网损下降率增加了约17%，并且计算时间略短；对平衡节点进行潮流计算，无功功率比优化前大幅度降低，综合经济条件及优化结果等方面充分显示出算法的有效性。

4 结论

4.1深入研究蚁群算法，对蚁群算法的信息素加权改进，验证算法的可行性，比常规蚁群算法在收敛速度上具有一定的优势。

4.2针对优化过程中易出现陷入局部最优解、搜索速度慢的情况，采用多智能体系统与改进蚁群算法的结合，经过实验对比验证，可以较快的达到搜索到全局最优解，即降低网损。

4.3利用遗传算法与多智能体蚁群算法进行对比，笔者的算法有在运算速度和优化结果上均有较好的优势。