分形与连分数

闫月静，李 核，刘 丰

（吉林师范大学 数学学院，吉林 四平 136000）

分形与连分数

闫月静，李 核，刘 丰

（吉林师范大学 数学学院，吉林 四平 136000）

分形几何学以非规则几何形态为研究对象，在数论中有着重要的应用.连分数的展式具有分形集结构的自相似性，可以估算其部分商满足一定条件下的Hausdorff维数.

分形;连分数；Hausdorff测度；Hausdorff维数

1 分形理论

1.1 分形的定义

在20世纪70年代，Mandelbrot为了表征复杂图形和复杂过程引入了“分形”(fractal)一词，它的原意是指不规则的、支离破碎的物体，随后又将其引入到自然学科领域，逐步形成了以非规则几何形态为研究对象的分形几何学.

在1982年，Mandelbrot将分形定义为拓扑维数大于Hausdorff维数的集合.之后，Mandelbrot又给出了分形更广泛的定义，即局部和整体以某种方式自相似的图形，强调了图形中的局部与整体间的自相似性.迄今为止，分形还没有严格的定义.

一般地，具有如下典型性质的集F称为分形：(ⅰ)集F在任意小的尺度下都有精细的结构；

(ⅱ)集F是极不规则的，它不能用传统的欧几里德空间的集合语言进行描述，即它既不是某些方程的解集又不是满足某些条件的点的轨迹；

(ⅲ)集F具有结构上的自相似性；

(ⅳ)集F的分形维数大于其拓扑维数；

在大多数的情况下，分形集F的定义很简单，并且可以通过变换相应的迭代关系而产生.

2 Hausdorff测度

在Rn中，∀U⊂Rn,U≠Ø，U的直径为|U|=sup{|x-y|:x,y∈ U}，即U内任何两点距离的最大值.若且对∀i都有，则称{Ui}为F的一个δ-覆盖.设∀F⊂Rn，s≥0，∀δ>0，定义

对∀F⊂Rn此极限都存在，我们称Hs(F)为F的s-维Hausdorff测度.

3 Hausdorff维数

2 连分数

分形在经典数论中的例子就是连分数，可以利用连分数的展开式来定义数集.

2.1 连分数的定义

任意一个不是整数的数x都可以写成x=a0+1/x1，这里a0是一个整数，并且x1>1.类似地，如果xi不是整数，那么x1=a1+1/x2，这里x2>1，所以x=a0+1/(a1+1/x2)，以这种方法进行下去，对每个k，x=a0+1/(a1+1(…1/(ak-1+1/xk))).

假设在每一步xk都不是整数则称整数序列a0,a1,a2,…（可以是有限项也可以是无限项）是x的部分商，并记

为x的连分数的展式，或记为[a0,a1,a2,a3,…]的形式.

连分数的展式在结构上很好的体现了分形集的精细结构，以及其在比例上的自相似性.

2.2 连分数的基本性质及应用

性质1 有理数可以展开成有限项连分数，无理数可以展开成无限项连分数.

性质2 具有整系数的二次方程的根都有周期性的部分商（即二次根式）[6].

例2 x2+4x-2=0的根

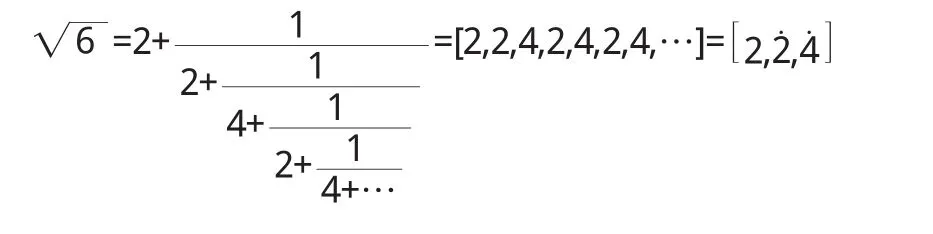
性质3 已知周期性的部分商，可以求出无理数.

3 连分数分形集的Huasdorff维数

利用分形的自相似性，也可以定义分形集.设D⊂R，且D为闭集，映射S:D→D，如果∀x,y∈D,∃c,0

在连分数的部分商上加一些条件，定义出来的数集经常是分形；改变加在部分商上的条件可以得到作为某些变换的不变集的其他分形，并且可以估计其Hausdorff维数.

例5 设F是正实数组成的数集，x∈F，且x具有无穷的部分分式展开式，且它们的部分商都等于1或2.那么F是分形，且0.44

〔1〕刘硕.分形图形的代数语言系统研究[D].兰州大学,2011.〔2〕Mandelbrot B B.The Fractal Geometry of Nature[M]. San Francisco:Freeman.1983,41-45.

〔3〕宛莹.多重分形理论及其在中国股票市场中的应用研究[D].东北大学,2007.

〔4〕丁伟业.连分数部分商的分形维数[D].华中科技大学, 2011.

〔5〕何雅.连分数及其基本性质[J].长江职业技术工程学院学报，2004,3(21).

〔6〕袁明豪,严培胜,张清芳.有限简单连分数的几个应用[J].黄冈师范学院学报，2004,6(23).

〔7〕秦静,张光明.分形自相似的一些应用[J].山东师大学(自然科学版),1998,12(13).

〔8〕赵义超,秦永华.循环简单连分数的定理证明[J].九江学院学报(自然科学版),2005（3）.

O29；O156

A

1673-260X（2014）04-0001-02