天然气管道氮气隔离混气长度研究

黄启玉， 曹鑫鑫， 唐骏琪， 许琛琛， 兰 浩

(1.中国石油大学(北京)油气储运工程系，北京 102249； 2.中国石油管道公司，河北廊坊 065000)

天然气管道氮气隔离混气长度研究

黄启玉1， 曹鑫鑫1， 唐骏琪1， 许琛琛2， 兰 浩2

(1.中国石油大学(北京)油气储运工程系，北京 102249； 2.中国石油管道公司，河北廊坊 065000)

基于一维混合模型研究天然气管道投产过程中气体的混合规律，利用Taylor、Taylor-CW、G.R.I 3种不同方法分别计算出气体扩散系数及投产过程中形成的天然气-氮气混气段长度，分析了管道置换过程中影响混气长度的主要因素，包括管长、管径及流速。由Taylor-CW方法计算出的结果与现场数据最为接近，用该方法验证国内3条已投产管道所得的相对误差分别为39.7%、23.4%、22.0%。

天然气管道； 氮气隔离； 混气长度； 现场对比

天然气管道投产时，为避免天然气与空气直接接触达到天然气的爆炸极限造成安全隐患，需预先在管道中封存一段氮气，将天然气与空气隔离。气体运行过程中，由于管线内部存在速度梯度和浓度梯度，管道内会形成两段混气段——氮气-空气混气段、天然气-氮气混气段。故管道内预存足够的氮气量，才能够保证在整个投产过程中天然气与空气均处于隔离状态。

目前，研究混气长度影响因素及变化规律的主要方法是运用FLUENT软件对气体扩散的过程进行模拟，初始设定的影响因素有气体种类、流态、管长、管径、流速、背压。模拟过程中，采用控制变量法，改变其中一个变量，根据所得结果分析混气长度的影响因素及变化规律。经研究得出：天然气-氮气与氮气-空气两种混气长度相差不大；湍流情况下的混气长度远短于层流状态下的；混气长度均随着管径、管长、流速及背压的增大而增大，与管径成正比、与管线长度的二分之一次方成正比[1-6]。

计算混气长度时，利用FLUENT软件对天然气管道内气体的掺混进行模拟，得出相应的混气长度计算拟合公式，利用该公式对特定长度、管径、流速的管道混气长度进行预算[7]。另有学者利用类似的方法对天然气管道置换的混气过程进行模拟，得出另一拟合公式[8]。前者计算结果与现场数据偏差较大，一般为实际数据的2倍以上；后者的误差小于前者，但在不同的管道参数下其计算结果不稳定。

基于气体扩散的一维模型，可利用Taylor、Taylor-CW、G.R.I 3种不同的方法编程计算出天然气管道置换过程中形成的两种混气段的长度。利用该方法计算国外8条管道混气长度并与实际数据进行对比，得出结论：G.R.I方法优于其余两种[9]。另有学者基于二维模型编程计算，但未将计算结果与现场数据进行对比分析，无法保证计算结果与管线现场情况相符[10]。

目前，天然气管道实际投产所需注氮量主要依据经验确定。对于短距离管道，所需氮气量根据管容与置换压力确定；对于长距离管道，氮气封存长度一般取待置换管线全长的20%[11]。不难发现，现场经验方法造成了一定人力、物力的浪费，且具有较大的盲目性。因此，为确定封存氮气量，需对天然气与氮气、氮气与空气的混合情况进行计算，得出所需氮气的最小用量。该研究以天然气-氮气混气段的变化为例，假设气体间仅存在轴向掺混，利用Taylor、Taylor-CW、G.R.I. 3种不同方法分别计算出气体扩散系数及天然气-氮气混气段长度变化情况，并将计算结果与国内外实际投产管线现场数据对比分析，得出相应结论。

1 理论分析及编程

仅考虑轴向气体的掺混，忽略径向速度、浓度的不均匀性及重力影响，建立一维氮气对流扩散模型，确定边界条件和初始条件，得出相对应的气体扩散理论公式[12]，当k≫u时，该扩散过程为对流占优扩散过程[13]，用到的气体扩散方程、初值条件及边界条件如下：

(1)

x(l,0)=0, 0≤l≤1

x(0,t)=1,t>0

x(1,t)=0,t>0

在初值条件下，对流方程的精确解为[14-18]:

(2)

根据式(2)理论公式，确定气体扩散系数后，即可求得特定管道的混气长度。目前有3种对流扩散系数：Taylor扩散系数、Taylor-CW湍流扩散系数、G.R.I湍流扩散系数[9]。

Taylor扩散系数： 层流状态下：

(3)

湍流情况下：

(4)

式中，k为层流扩散系数，m2/s；u为管内平均流速，m/s；r为管道半径，m；D1为分子扩散系数，m2/s；um为圆管界面的主体平均流速，m/s；Re为雷诺数(3×104≤Re≤106)。

Taylor-CW湍流扩散系数：

(5)

其中，圆管湍流摩擦系数f由Colebrook-White公式迭代计算得出：

(6)

式中， Re为管道内气体流动雷诺数；δ为管道绝对当量粗糙度，m；r为管道半径，m；um为圆管界面的主体平均流速，m/s。

G.R.I湍流扩散系数：

(7)

式中，k为G.R.I湍流扩散系数，m2/s；v为置换流速，m/s；d为管道直径，m。

基于上述理论分析，通过编程定量研究管道投产过程中天然气与氮气的掺混情况。将整条管线分为若干个步长，计算单个步长管道内气体混合后气体浓度分布情况，将上一步长终点处的浓度作为下一步长起始点的浓度，循环计算直至整条管段置换完毕。计算出最终天然气浓度为98%的点坐标，由此确定管段置换完毕后的混气长度(置换过程的混气段包括氮气-空气混气段和天然气-氮气混气段，本数学模型认为气体种类对混合长度的影响很小[4]，故氮气-空气混气段长度等于天然气-氮气混气段长度，总混气长度取编程计算一段混气长度的2倍)，具体流程见图1。

利用Matlab软件中GUI功能，设计计算界面，如图2所示。根据投产现场数据，在界面左侧可输入动力黏度、密度、绝对当量粗糙度、管道直径、平均流速及管长等已知参数，可计算出流体流动状态表征参数雷诺数Re在126 172～340 045内，远大于临界雷诺参数2 000，故编程时默认流动状态为湍流。在界面右侧可选择不同的湍流扩散系数计算方法，最终的计算结果从混气长度一栏中输出。

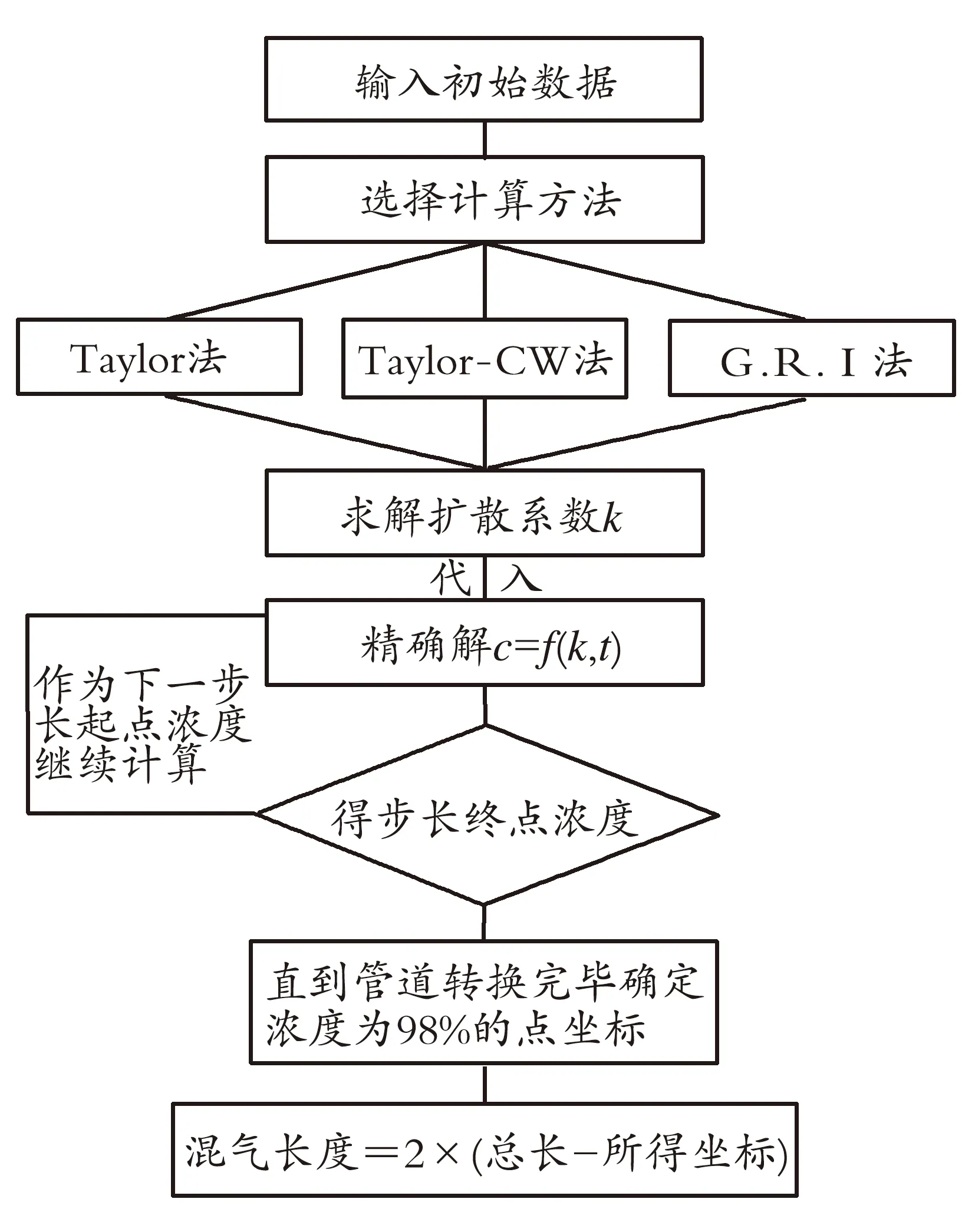
图1 编程流程图

Fig.1Programmingflowchart

图2 计算界面

Fig.2Graphicaluserinterface

2 混气长度影响因素分析

利用一维编程软件对天然气管道氮气置换过程中混气长度变化规律进行分析，对影响天然气管道投产时混气段长度及混气量的因素进行了研究，确定了管长、管径、流速等因素对混气量的影响。

2.1管长

为分析管长对混气长度的影响规律，在管径762 mm、置换流速9.25 m/s等条件相同的情况下，取一定的管长梯度，分别计算其对应的混气长度，如图3所示。

由图3可以看出，在管径、置换流速等条件一定的情况下，混气长度随管长的增大而增大；以Taylor算法和G.R.I.算法为例，管长增加至其2倍，混气长度平均增长率分别为41.42%和41.43%。置换初期，混气长度增加速率较大，随着管长的增加，混气长度的增加速率变小。分析其原因，管长增加，气体在管道中的掺混时间变长，形成的混气长度也随之变长。之后，气体内部浓度梯度变小，对流扩散强度变小，混气长度增加速率变小。

图3 管长对混气长度的影响

Fig.3Effectofthepipelinelengthonthegas-mixingsectionlength

2.2管径

为研究管径对混气长度的影响，取长度相同、管径分别为406、508、660、711、1 016 mm的不同管道，设置置换流速5 m/s，其余条件均相同，用Taylor-CW法计算混气长度，结果如图4所示。

图4 管径对混气长度的影响

Fig.4Effectofpipelinediameteronthegas-mixingsectionlength

由图4可以看出，在管长、置换流速等条件一定的情况下，管径增大，混气长度增大。同一管长条件下，管径增大至其2倍，混气长度增长约36.7%。由于管径增大，两种气体的接触面面积增大，气体分子扩散空间增大，故气体的湍流扩散系数也随之增大，混气长度越长。

2.3流速

为研究流速对混气长度的影响，取管径1 016 mm、管长82 km的管段，利用Taylor-CW方法计算其在不同置换流速下(湍流)的混气长度，如图5所示。

由图5可以看出，在管长、管径等条件一定的情况下，气体流速增大，混气长度减小，且变化率不断降低，这一结论与文献[4]中的二维数值模拟的结论一致。

图5 置换流速对混气长度的影响

Fig.5Effectofnitrogenvelocityonthegas-mixingsectionlength

3 计算结果验证

3.1国外管道混气长度验证

用Taylor、Taylor-CW、G.R.I 3种方法计算混气长度，并与现场数据进行对比，选取计算结果与现场情况最为符合的方法。利用编写的软件对美国8条管道混气长度进行验证，将其与现场实际混气长度对比，结果见表1。

表1 3种方法计算结果与实际数据对比结果Table 1 Comparison of calculated and field data for gas-mixing section length with three methods

由表1可以看出，G.R.I方法确定的混气长度平均误差最小；但针对2#～5#管道，由Taylor-CW方法确定的混气长度与现场数据更为相符，最小的误差仅有3%。

国外8条管道长度均较短，其中6条均在2～26 km内，其余两条管长分别为86.7、121.7 km；管道投产气体平均流速差异较大，值在6.83～21.24 m/s内。我国国内投产管道一般为数百甚至上千公里，根据《天然气管道运行规范》 (SY/T5922—2003)规范，气体的推进速度一般在3～5 m/s内[19]，实际投产时气体平均流速一般在5 m/s左右，最大不超过8 m/s，故国外管道的投产数据与国内管道有一定差距。

3.2国内管道混气长度验证

选取国内3条管道，用Taylor、Taylor-CW、G.R.I 3种方法计算混气长度，并与现场数据进行对比分析，选取计算结果与现场情况最为符合的方法。该3条管线均已成功投产，长度分别为380、201、296 km，管径均为1 016 mm，气体平均速度均为5 m/s。3条管线的混气长度变化趋势线与现场数据的对比结果如图6所示。

图6 不同管线计算值与现场数据对比结果

Fig.6Comparisonofcalculatedandfielddataforgas-mixingsectionlengthondifferentpipeline

由图6可以看出，现场数据分布较为零散，但总体呈现不断增加的趋势，且主要分布在由Taylor-CW方法计算所得的曲线两侧；该方法下3条管道的混气长度计算结果的误差分别为39.7%、23.4%、22.0%，远小于其余两种方法，故3种方法中Taylor-CW最能反映现场实际情况。

通过分析，计算结果与现场数据存在误差的原因有：

a) 管道敷设高程起伏变化，上坡段会加剧气体的混合。此外，由于天然气管道干燥不彻底，管道内低洼处会存在积水，气体压力必须足够大才能通过该积水段，故导致气体被压缩，混气量增加。

b) 投产过程中首站不断加压，流量增大，管内气体流速不断增加，导致混气量变化。计算过程中流速均为5 m/s，与实际流速有偏差。

c) 现场人工检测操作、记录数据存在误差。

4 结论

基于一维气体混合模型，对天然气管道置换过程中天然气-氮气混气长度进行了预测计算，利用编写的软件对国内外共11条管道混气长度进行验证，并将计算结果与现场数据进行对比，得出以下主要结论：

1) 对于国外管道，所选取的管道长度总体偏小，且气体平均流速大小不一，差异较大，故得G.R.I方法确定的混气长度平均误差最小；但针对部分单组数据，由Taylor-CW方法确定的混气长度与现场数据更为相符，误差在3%～39%；

2) 对于国内管道，所选取的管道长度较长，气体平均流速均为5 m/s，接近于国内管道投产情况，故得Taylor-CW方法所得的混气长度曲线与现场数据拟合较好，3条管道计算结果的误差分别为39.7%、23.4%、22.0%；

3) 影响管道置换过程中混气长度的因素主要有管长、管径、流速。混气长度随管长的增大而增大，管长增加至其2倍，混气长度增长约41.5%；混气长度随管径的增大而增大，同一管长条件下，管径增大至其2倍，混气长度增长约36.7%；混气长度随气体流速的增大而减小，且变化率不断降低；

4) 管道实际投产过程中，混气长度受高程、流速、压力等多种因素影响，故呈现一定的波动性，非单调增长趋势。

[1] 付春丽. 输气管道氮气置换混气长度的影响因素[J]. 油气储运,2011, 30(2): 94-96.

Fu Chunli. Influencing factors of gas-mixing length during nitrogen purging & packing course of gas pipeline [J]. Oil & Gas Storage and Ttransportation, 2011, 30(2): 94-96.

[2] 丛蕊,刘树林,唐友福，等.大口径天然气管道置换规律研究[J].科学技术与工程.2010, 10(24): 6016-6020.

Cong Rui,Liu Shulin,Tang Youfu,et al. The study of replacement law in large diameter natural gas pipeline [J]. Science Technology and Engineering， 2010, 10(24): 6016-6020.

[3] 胡其会. 天然气管线氮气置换混气段规律研究[D]. 东营：中国石油大学(华东), 2006.

[4] 郭小龙, 白博峰, 刘茂龙，等. 管道气体置换混合长度变化规律研究[J]. 化学工程， 2009, 27(5): 23-25.

Guo Xiaolong, Bai Bofeng, Liu Maolong, et al.Study on length of mixed region during gas purging in pipeline[J]. Chemical Engineering(China),2009, 27(5): 23-25.

[5] 申龙泽, 姚化伟. 长输天然气管道干空气干燥最优长度优化计算[J]. 当代化工, 2011,40(4):433-435.

Shen Longze, Yao Huawei. Optimization length of long-distance gas pipeline in dry air[J]. Contemporary Chemical Industry,2011,40(4): 433-435.

[6] 冯云飞, 吴明, 闫明龙，等. 含硫天然气泄漏扩散的三维数值模拟[J].辽宁石油化工大学学报, 2012,32(1):41-45.

Feng yunfei, Wu Ming, Yan Minglong, et al.3D numerical simulation on natural gas containing sulfur pipeline leakage and the diffusion[J]. Journal of Liaoning Shihua University, 2012, 32(1): 41-45.

[7] 薛继军, 张鹏云，王俊奇.输气管道投产置换注氮量计算方法[J]. 天然气工业, 2007, 27(12): 133-135.

Xue Jijun, Zhang Pengyun, Wangjunqi. Calculation method for injection capacity of nitrogen gas during pipeline replacement[J]. Natural Gas Industry, 2007, 27(12): 133-135.

[8] 曹学文, 付春丽. 海底输气管道投产氮气用量计算方法研究[J]. 中国海上油气, 2010, 22(6): 417-419.

Cao Xuewen, Fu Chunli. Calculating the injection volume of pre-commissioning nitrogen in offshore gas pipeline[J]. China Offshore Oil and Gas, 2010, 22(6): 417-419.

[9] 刘凡, 江楠. 管道氮气置换混气长度分析研究[J].石油化工设备.2012, 41(1): 11-14.

Liu Fan, Jiang Nan. Investigation on length of mixed gas for nitrogen replacement in pipeline[J]. Petro-Chemical Equipment, 2012, 41(1): 11-14.

[10] 张奕. 新建天然气管线氮气置换过程动态模拟分析[D].成都：西南石油大学，2011.

[11] 孟军政, 李银凯, 石刚，等.浅谈天然气管道投产中气推气置换法[J].油气田地面工程,2008,27(10): 46-47.

Meng Junzheng, Li Yinkai, Shi Gang, et al. Discussion on natural gas pipeline gas-against-gas replacement method [J].Oil-Gas Field Surface Engineering, 2008,27(10): 46-47.

[12] Johnson J E. Pipeline purging principles and practice [J]. Journal of Offshore Mechanics and Arctic Engineering, 1998, 120(4): 249-256.

[13] 陆金甫.对流占优扩散问题的特征线法—差分法计算格式[J]. 计算物理, 1989,6(4): 486-493.

Lu Jinfu. Numerical schemes of the characteristics-difference method for convection-dominated diffusion problems[J]. Chinese Journal of Computational Physics, 1989,6(4): 486-493.

[14] Taylor G I. The dispersion of matter in turbulent flow through a pipe [J]. Proc .Roy .Soc .A，1954(223): 446-468.

[15] Clayton C G, Webb J W, Whittaker J B. The dispersion of gas during turbulent flow in pipe[J]. Brit. J. Appl. Phys.,1963, 14(11): 790-794.

[16] Taylor G I. Diffusion and mass transport in tubes[J]. Proc. Phys. Soc., 1954，LXVII (12B): 857-869.

[17] Taylor G I. Dispersion of soluble matters in solvent flowing slowly through a tube[J]. Chemical Engineering Science, 2004(59): 3929-3944.

[18] Perkins T K, Euchner J A. Safe purging of natural gas pipeline[J]. SPE Production Engineering, 1998, 3(4):663-668.

[19] 杨喜柱, 李玉清, 王道友,等. 埕港输气管道氮气置换投产工艺参数确定[J]. 石油工程技术, 2010(8): 73-74.

Yang Xizhu, Li Yuqing, Wang Daoyou, et al. Determination of the pre-commissioning parameters with nitrogen replacement in Chenggang gas pipeline[J]. Petroleum Engineering Technology, 2010(8): 73-74.

(编辑 王亚新)

Study on the Gas-Mixing Section Length during Nitrogen Replacement of Natural Gas Operation in Gas Pipeline

Huang Qiyu1, Cao Xinxin1, Tang Junqi1, Xu Chenchen2, Lan Hao2

(1.DepartmentofOilandGasStorageandTransportation,ChinaUniversityofPetroleum,Beijing102249,China; 2.ChinaNationalPetroleumCorporationPipelineCompany,LangfangHebei065000,China)

The gas diffusion coefficient and therefore gas-mixing section length was studied by using one-dimension mathematical model in combination with three different methods for calculating gas diffusion coefficient (Taylor, Taylor-CW and G.R.I). In addition, the predominant factors in affecting the gas-mixing section length were also investigated, including pipeline length, diameter and velocity of the flow. And the comparison between the calculation results and field data show that Taylor-CW method can reflect the field practice better. The relative errors of the results for three domestic pipelines are 39.7%, 23.4% and 22.0%, respectively.

Natural gas pipeline; Nitrogen gas replacement; Gas-mixing section length; Data comparison

1006-396X(2014)01-0084-07

2013-06-05

：2013-09-09

国家自然科学基金项目“油包水型乳状液蜡分子扩散和蜡晶颗粒沉积机理研究”(51374224)。

黄启玉(1969-)，男，博士，研究员，从事长距离输送管道技术和油库安全方向研究;E-mail:huang_qi_yu@sina.com。

TE832

： A

10.3969/j.issn.1006-396X.2014.01.017