不同随机波影响因子下张力腿平台动力响应

刘为民，谷家扬，卢燕祥

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

不同随机波影响因子下张力腿平台动力响应

刘为民，谷家扬，卢燕祥

(江苏科技大学 船舶与海洋工程学院，江苏 镇江 212003)

采用时域耦合法对某传统式张力腿平台进行非线性动力响应研究，重点讨论不同随机波有义波高、谱峰周期和入射波方向对张力腿平台各自由度运动响应和顶端张力的影响。结果显示，本文各工况各自由度最大位移均满足设计要求。纵荡、垂荡和首摇运动幅值对有义波高较为敏感；平面内运动对谱峰周期较敏感，而谱峰周期对平面外运动影响不大；平面内运动对入射波角度较敏感。纵荡和首摇为低频运动，垂荡和纵摇为高频运动，其中垂荡与纵荡相耦合；由于高频载荷引起平台升沉、横摇和纵摇运动，而这3种运动又作用于张力腿轴向振荡，从而使得张力腿顶端张力表现为高频响应。

时域耦合；高频；低频；非线性；运动响应

0 引 言

张力腿平台是一种半顺应半刚性平台，拥有较为出色的运动性能，因此，在深海油气开发中占据重要一席之地[1]。相关专家、学者对张力腿平台某些方面进行研究和探讨，王世圣等[2]利用SESAM软件对南海某张力腿平台进行了六自由度运动和静力分析，结果表明该平台适应南海1 500 m水深复杂海洋环境并拥有良好运动性能。Y.M.Low[3]采用等效线性化方法对某张力腿平台进行耦合动力响应研究，并对时域和频域计算结果进行分析。M.R.Tabeshpour等[4]采用扰动法对规则波下轴向载荷变化对某张力腿平台运动性能影响进行研究，结果得出位移轨迹和时间历程图。CHEN Xiao-hong等[5]采用4种不同方法(实验测量、准静态法、基于辐射和绕射理论的COUPLE软件和WAMIT软件)对某迷你型张力腿平台进行研究和比较，结果显示准静态法仅能在波频范围内进行预报，而COUPLE在各波频内均具有良好计算结果。S.Chandrasekaran等[6]采用Stokes理论对不同浪向下三角形布置的张力腿平台进行了动力响应研究，结果表明浪向角对各自由度运动(除垂荡)影响较大，而直线型运动为非线性运动。S.Chandrasekaran等[7]对不同惯性力系数和拖曳力系数的某三角形张力腿平台进行了规则波非线性动力响应研究，重点讨论了上述系数对纵荡、纵摇和垂荡的影响。任顺利等[8]采用SESAM软件对不同刚度影响下的张力腿平台运动进行响应分析，结果显示对张力腿平台初步设计具有一定的参考作用。

国内外学者主要对规则波下、不同耦合方法和不同张力腿平台本身参数影响下的动力特性进行研究，对于不同随机波影响因子下的动力响应研究较少。因此，本文采用时域耦合方法对不同随机波下张力腿平台非线性动力响应进行研究。由于南海海洋环境复杂性，本文着重对不同特征波高、谱峰周期下张力腿平台运动和张力腿顶端张力变化进行分析和讨论。

1 运动方程

浮式海洋结构物运动方程如下[9-11]：

(1)

(2)

式中：M为频率相关矩阵；m为浮体质量矩阵；A为频率相关附加质量；C为频率相关势流矩阵；D1为线性阻尼矩阵；D2为二阶阻尼矩阵；f为速度矢量函数；K为水静力刚度矩阵；x为位移矢量；q为矢量激励力；ω为频率。

2 张力腿平台模型概述

本文以我国南海所设计某传统式张力腿平台为研究对象，结构主体分别由4个立柱和4个浮箱组成，该平台主体关于中纵剖面和中横剖面对称，其示意图和张力腿布置及编号分别如图1和图2所示。本文仅考虑张力腿对主体作用，而忽略其他附属结构物对主体作用。张力腿平台主体主要参数和张力筋腱参数分别如表1和表2所示。

图1 张力腿平台示意图Fig.1 Plot of TLP

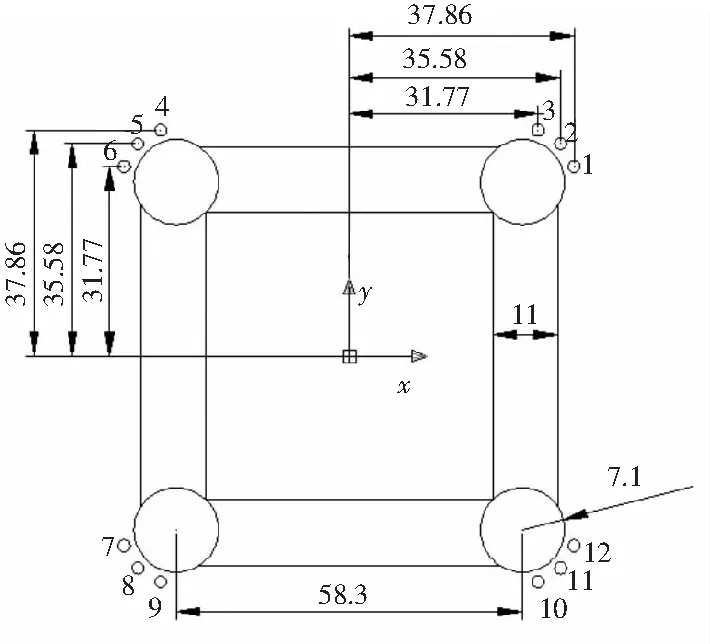
图2 张力腿布置及其编号Fig.2 The arrangement and makers of tendons

参数数值参数数值参数数值重量/t20950立柱半径/m7.1重心距水线面高度/m9.25排水量/t33525立柱高度/m46.6横摇回转半径/m29.15总预张力/t12575立柱间距/m58.3纵摇回转半径/m29.15作业吃水/m26.6浮箱宽度/m11首摇回转半径/m32.1张力腿数目12浮箱高度/m8工作水深/m1000

表2 张力筋腱参数(每根)

由于随机波可视为由许多规则波叠加而成，因此采用波浪谱对海面进行模拟。另外，由于深海海域拥有不同成长阶段波，因此，本文采用JONSWAP谱。根据有义波高(Hs=6 m,8 m和10 m)和谱峰周期(Tp=10 s,12 s和14 s)进行不同组合，进而对不同入射波方向(0°, 22.5°, 45°)下的张力腿平台动力响应进行研究。各计算工况表示为ID*H*T*形式，如ID0H6T10表示入射波角度0°，有义波高6 m和谱峰周期10 s计算工况。

3 计算结果分析

本文利用SESAM软件，通过时域耦合方法对不同随机波下张力腿平台非线性动力响应进行研究，根据规范(漂移≤工作水深5%，升沉≤±1 m，摇摆≤±3°)判断各工况是否满足设计要求。

3.1 有义波高对张力腿平台运动影响分析

相同入射波方向、相同谱峰周期、不同有义波高下(ID0H6T10、ID0H8T10和ID0H10T10)各自由度运动统计结果如图3～图6所示。对图3～图6进行分析可知，随着有义波高的增大，纵荡、纵摇和首摇的最大响应、最小响应和平均值绝对值增大较明显，这意味着张力腿平台随着有义波高的增大，纵荡、纵摇和首摇运动幅值逐渐增大；平衡位置相对初始位置也逐渐变大。各自由度标准差值随着有义波高增大而逐渐增大，即张力腿平台随着有义波高增大愈来愈不稳定。通过对图3分析可知，张力腿平台沿x轴正方向力随着有义波高增大而增大，导致纵荡运动正方向位移较负方向位移值大，且增长率更快，体现了纵荡运动慢漂特点。从图4可分析，由于垂荡运动与纵荡运动耦合，使得z轴负方向力随有义波高增大而增大，因此其最小响应较最大响应增长较快；又垂荡运动最大响应稍有增大趋势，即张力腿平台随有义波高的增大，张力腿平台平衡位置逐渐下移。通过图5可知，纵摇平均值几乎为0，即平衡位置在初始位置附近处作来回振荡运动。综上，纵荡、垂荡和首摇最大响应对有义波高较为敏感，且垂荡和首摇最小响应对有义波高较为敏感。

图4 不同有义波高下垂荡运动统计值Fig.4 Statistics of heave motion under different significant wave heights

图5 不同有义波高下纵摇运动统计值Fig.5 Statistics of pitch motion under different significant wave heights

图6 不同有义波高下运动首摇统计值Fig.6 Statistics of yaw motion under different significant wave heights

不同自由度运动频谱反映的是不同频率下能量谱分布情况、各自由度高低频运动等。图7～图10所示为不同有义波高下不同自由度运动频谱，从图7～图10分析可知，同一频率下能量值随着有义波高的增大而逐渐增大；在同一频率下，峰值有轻微相位差。从图7分析可知，纵荡频谱图中只有1个峰值，且频谱峰值随着有义波高的增大而逐渐增大，这是张力腿平台沿x轴方向受力呈直线型增长的缘故。纵荡频谱图中0.6 rad/s处呈现出较小能量峰值，这是平面外高频运动所引起。从图8分析，由于垂荡运动与低频纵荡运动相耦合的缘故，导致垂荡运动在0.05 rad/s附近处显示出较高能量值。另外，垂荡峰值随着有义波高的增大而有所增大，其中有义波高10 m尤为明显。由图10所示，首摇运动为低频运动，与其固有周期(高于40 s)相对应，同一频率下能量值随有义波高的增大成倍增长，峰值所对应频率无明显相位差特点。

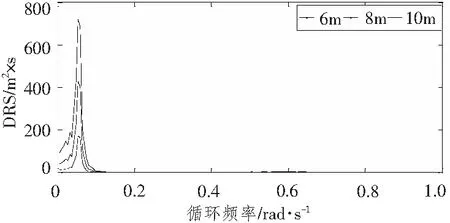
图7 不同有义波高下纵荡运动频谱Fig.7 PSD of surge under different significant wave heights

图8 不同有义波高下垂荡运动频谱Fig.8 PSD of heave under different significant wave heights

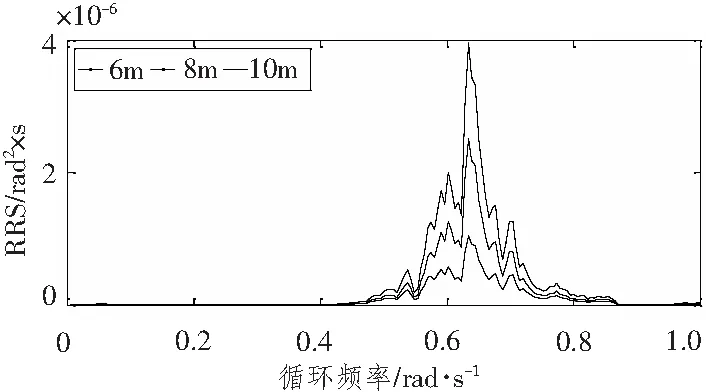
图9 不同有义波高下纵摇运动频谱Fig.9 PSD of pitch under different significant wave heights

图10 不同有义波高下首摇运动频谱Fig.10 PSD of yaw under different significant wave heights

3.2 谱峰周期对张力腿平台运动影响分析

相同入射波方向、相同特征波高，不同谱峰周期(ID0H6T10、ID0H6T12和ID0H6T14)下各自由度运动统计结果如图11～图14所示。对图11～图14进行分析可知，纵荡和首摇运动下各统计值变化较为明显，而垂荡和纵摇运动变化较小。对图11分析，随着谱峰周期的增大，纵荡运动最大响应、平均值、标准差逐渐减小，而最小响应无明显变化趋势，即随着谱峰周期的增大，张力腿平台平衡位置逐渐趋向于初始位置，且纵荡运动振荡激烈程度降低。从图12可知，垂荡运动中各自由度运动无明显变化规律，在-0.15 m附近处作来回振荡运动，即垂荡运动对谱峰周期敏感性不强。对图13进行分析，纵摇运动各统计值无明显变化，张力腿平台在初始位置作摇摆运动。对图14进行分析可知，首摇最大响应和最小响应绝对值随着谱峰周期的增大而减小，间接体现了张力腿平台平衡位置逐渐向初始位置处移动；另外，谱峰周期12 s和14 s下标准差几乎为0，即谱峰周期10 s下首摇运动较其它两谱峰周期下激烈。综上，平面内运动对谱峰周期最为敏感，而谱峰周期对平面外运动影响不大。

图11 不同谱峰周期下纵荡运动统计值Fig.11 Statistics of surge motion under different peak spectral periods

图12 不同谱峰周期下垂荡运动统计值Fig.12 Statistics of heave motion under different peak spectral periods

图13 不同谱峰周期下纵摇运动统计值Fig.13 Statistics of pitch motion under different peak spectral periods

图14 不同谱峰周期下运动首摇统计值Fig.14 Statistics of yaw motion under different peak spectral periods

图15 不同谱峰周期下纵荡运动频谱Fig.15 PSD of surge under different peak spectral periods

图17 不同谱峰周期下纵摇运动频谱Fig.17 PSD of pitch under different peak spectral periods

图18 不同谱峰周期下首摇运动频谱Fig.18 PSD of yaw under different peak spectral periods

图15～图18所示为不同谱峰周期下不同自由度运动频谱，从图15～图18分析可知，平面内运动频谱较平面外运动频谱较规则，变化规律明显；除纵荡运动外，其他频谱图中均有2个及2个以上峰值。从图15分析可知，随着谱峰周期的增大，相同频率下峰值逐渐减小，且谱峰所对应频率有增大趋势。从图16分析可知，垂荡运动频谱在较低频率下，谱峰变化与纵荡运动谱峰变化相对应，这是垂荡运动与纵荡运动耦合的结果；但垂荡运动为高频运动。对图17可分析，由于纵摇和垂荡所受荷载为高频荷载，因而表现为高频运动，且频谱变化复杂。对图18分析可知，谱峰值随着谱峰周期的增大而减小，谱峰周期10 s下谱峰较其他两谱峰周期下要大很多。综上，在谱峰周期小于等于10 s以下，各自由度运动也许对谱峰周期较为敏感，而谱峰周期大于等于12 s，敏感性降低；纵荡、首摇运动为低频运动，而垂荡和纵摇为高频运动。

3.3 同根张力腿顶端张力能量谱分析

图19和图20所示分别为张力腿(T1)顶端张力随有义波高和谱峰周期变化的能量谱。对图19和图20分析可知，张力腿(T1)在不同有义波高和谱峰周期下均为高频运动；不同有义波高影响下能量谱有明显变化规律，而不同谱峰周期下能量谱分布较为分散。对图19分析，张力腿(T1)顶端张力能量谱随有义波高的增加而逐渐增大，且各有义波高下顶端张力能量谱峰值所对应频率均约为0.62 rad/s。对图20分析可得，随着谱峰周期的增大，张力腿(T1)顶端张力能量谱峰值所对应频率逐渐减小，其频率分别约为0.62 rad/s、0.60 rad/s和0.58 rad/s。由于受篇幅限制，对不同影响因子下的其他张力腿能量谱分析就不作赘述。综上，张力腿(T1)对有义波高敏感性较高，而对谱峰周期敏感性较低。

图19 不同有义波高下张力腿(T1)顶端张力能量谱Fig.19 PSD of top tension of T1 under different wave directions

图20 不同谱峰周期下张力腿(T1)顶端张力能量谱Fig.20 PSD of top tension of T1 under different wave heights

3.4 浪向角对各自由度影响分析

表3所示为不同浪向角(0°，22.5°，45°)，特征波高6 m，谱峰周期10 s下张力腿平台各自由度运动最大响应、最小响应、平均值和标准差。最大响应和最小响应反映了张力腿平台运动幅度，平均值反映了张力腿平台平衡位置，标准差反映了张力腿平台在平衡位置周围的运动剧烈程度。从表3可分析，纵荡最大响应和最小响应绝对值、平均值和标准差均随着浪向角逐渐增大而减小，反映了张力腿平台随着浪向角逐渐增大，纵荡方向运动幅度逐渐减小，平衡位置逐渐向张力腿平台初始位置靠近，纵荡运动愈稳定，这是由于x方向分力随着浪向角增大而减小的缘故。相反，由于y轴方向分力随着浪向角逐渐增大，导致张力腿平台在横荡方向运动幅度增大，平衡位置离初始位置愈远，横荡运动越不稳定。由于垂荡与横荡/纵荡相耦合，使得垂荡方向各统计值变化不大。另外，首摇响应值在22.5°下的量级最大，其次是0°，最后是45°，说明首摇对浪向角敏感性较强。在浪向角45°下，纵荡与横荡、纵摇和横摇各统计值基本一致，这是因为在浪向角45°下，沿x，y轴及绕x，y轴分力相等。

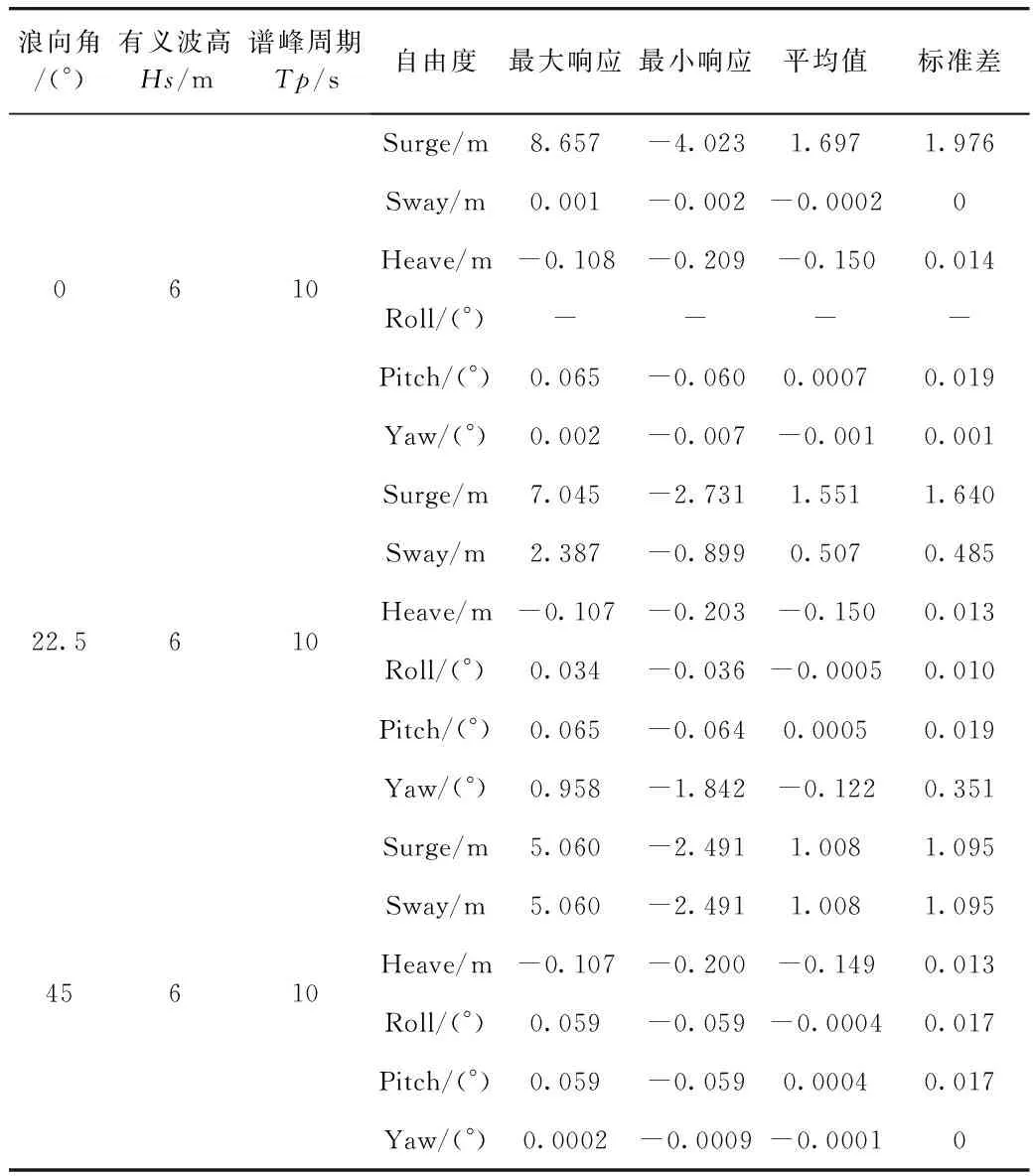
表3 不同浪向角张力腿平台六自由度响应比较

4 结 语

本文通过时域耦合法对某传统式张力腿平台进行非线性动力响应研究，主要讨论了不同有义波高、谱峰周期和入射波对六自由度响应影响，以及张力腿顶端张力变化情况。主要结论如下：

1)各工况各自由度最大响应均满足设计要求，保证了漂移≤工作水深5%，升沉≤±1 m，摇摆≤±3°；

2)纵荡、垂荡和首摇最大响应对有义波高较为敏感，而垂荡和首摇最小响应对有义波高较为敏感；平面内运动对谱峰周期较敏感，而谱峰周期对平面外运动影响不大；平面内运动对入射波角度较敏感；

3)纵荡和首摇为低频运动，垂荡和纵摇为高频运动，其中垂荡与纵荡相耦合；由于高频载荷引起平台升沉、横摇和纵摇运动，而这3种运动又作用于张力腿轴向振荡，从而使得张力腿顶端张力表现为高频响应；

4)随着有义波高的增大，各运动幅值逐渐增大，且频谱峰值也逐渐变大；随着谱峰周期的增大，纵荡和首摇运动幅值减小，且频谱峰值也逐渐减小；随着入射波方向由0°增至45°，纵荡运动幅值逐渐变小且越稳定，而横荡运动幅值逐渐增大且愈不稳定。

[1] CHRISTOPHER N.Mahoney and chad supan of wood group mustang.2012 Deepwater.Solutions & Records for Concept Selection.Offshore,2012.

[2] 王世圣,谢彬,李新仲.在南海环境条件下深水典型TLP的运动响应分析[J].中国造船,2011,52(1):94-101.

WANG Shi-sheng,XIE Bin,LI Xin-zhong.The motion response analysis of deep water typical TLP in environment conditions of south china sea[J].Shipbuilding of China,2011,52(1):94-101.

[3] LOW Y M.Frequency domain analysis of a tension leg pl-atform with statistical linearization of the tendon restoring forces[J].Marine Structures,2009:1-24.

[4] TABLEESHPOUR M R,GOLAFSHANI A A,SEIF M S.Second-order perturbation added mass fluctuation on vertical vibration of tension leg platforms[J].Marine Structures,2006,19:271-283.

[5] CHEN Xiao-hong,DING Yu,ZHANG Jun,et al.Coupled dynamic analysis of a mini TLP:comparison with measurements[J].Ocean Engineering,2006,33:93-117.

[6] CHANDRASEKARAN S,JAIN A K.Anupam gupta.inf-luence of wave approach angle on TLP′s response[J].Ocean Engineering,2007,34:1322-1327.

[7] CHANDRASEKARAN S,JAIN A K,CHANDAK N R.Inf-luence of hydrodynamic coefficients in the response behavior of triangular TLPs in regular waves[J].Ocean Engineering,2004,31:2319-2342.

[8] 任顺利,陈建民,梁艳霞.张力腿刚度对平台运动响应影响分析[J].石油矿场机械,2008,37(5):28-31.

REN Shun-li,CHEN Jian-min,LIANG Yan-xia.Influence of tether stiffness on TLP[J].Oil Field Equipment,2008,37(5):28-31.

[9] DNV,SESAM User Manual Wadam Version 8.2, 2010.

[10] DNV,SESAM User Manual HydroD Version 4.5, 2011.

[11] MARINTEK.SIMO-Theory Manual V3.6.2009.

Research on dynamic response of different irregular wave factors on TLP

LIU Wei-min，GU Jia-yang， LU Yan-xiang

(School of Naval Architecture and Marine Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

The time-domain coupling method is applied in this paper to study on nonlinear dynamic response of classical tension leg platform. Different irregular significant wave heights, spectral periods and incoming directions have influence on different degrees of freedom and top tension of tether, which is mainly discussed in this paper. The results demonstrate that the maximum displacements of all cases satisfy the requirements of rules. The amplitudes of surge, heave and yaw are sensitive to significant wave height. Motion in-plane is sensitive to spectral periods which have little influence on motion out of plane. Motion in-plane is also sensitive to incoming directions. Surge and yaw are low-frequency motions, and heave and yaw are high-frequency motions. Heave and surge have coupling motion each other. Due to heave, roll and pitch caused by high-frequency load which lead to vibration with high-frequency response of top tension in axis direction of tendon.

time-domain coupling;high-frequency;low-frequency;nonlinear;motion response

2014-03-19；

2014-04-08

国家自然科学基金资助项目(51309123)；江苏省高校自然科学研究资助项目(13KJB570002)；江苏省船舶先进设计制造技术重点实验室开放研究基金资助项目(CJ1203)。

刘为民(1979-)，女，讲师，主要研究方向为近海岸工程水动力性能。

TE951

A

1672-7649(2014)07-0058-06

10.3404/j.issn.1672-7649.2014.07.013