圆柱壳在径向冲击载荷作用下的动力响应

殷平化，孙昌将

(海军蚌埠士官学校 机电系，安徽 蚌埠 233000)

圆柱壳在径向冲击载荷作用下的动力响应

殷平化，孙昌将

(海军蚌埠士官学校 机电系，安徽 蚌埠 233000)

利用Hamilton原理得出轴向压力和径向冲击载荷作用下圆柱壳位移的运动微分方程，推导方程的解析解。通过数值计算，分析圆柱壳的位移随时间变化曲线，位移的幅频曲线以及应变随时间变化曲线和幅频曲线。数值计算结果表明，圆柱壳的径向和轴向位移要远大于周向位移；简谐激励频率为285 Hz，1 060 Hz，1 152 Hz，2 444 Hz，2 640 Hz，2 763 Hz，4 074 Hz时，径向位移幅值取值最大；简谐激励频率为285 Hz时轴向位移幅值取值最大；简谐激励频率为4 074 Hz时轴向应变幅值取得最大值；简谐激励频率为5 586 Hz，5 762 Hz，6 285 Hz时，周向应变幅值取值最大。

圆柱壳；冲击载荷；动力响应；轴向压力

0 引 言

在工程实践中，经常会遇到复杂壳体结构的动力响应问题。例如，超空泡体在水下高速航行的时候，一方面受到流体阻力和推进力的作用，另外由于空泡形态的改变及运动的稳定性，超空泡体的局部会与流体/空泡交界面发生接触，因而产生冲击作用。目前，对于复杂壳体结构的动力响应进行理论分析的文章不多，更多的只是研究单纯的轴向受力圆柱壳的稳定性和振动特性。例如文献[1-3]根据Flügge，Sander，Love，Donnell方程，应用模态叠加法推导出Mathieu方程，并利用三角级数对圆柱壳的动态稳定特性进行了分析，对不同几何参数下的4种方程的结果进行了比较。文献[4]利用Flügge 壳体理论分析了正交各向异性圆柱壳在轴向压力作用下的静态屈曲和固定轴向力作用下的壳体振动特性。文献[5]利用Flügge 壳体理论分析了正交各向异性圆柱壳受到静水压力和某点受到径向简谐载荷时的稳态动力响应。文献[6]利用有限元方法研究了冲击载荷作用下超空泡水下航行体的结构响应。本文利用Hamilton原理导出圆柱壳在轴向压力和径向区域均匀分布载荷作用下关于位移运动微分方程，通过数值计算分析了圆柱壳的位移响应和应变响应。

1 理论分析

图1为本文所讨论的圆柱壳的示意图。

L为圆柱壳长度，R为中面半径,h为厚度，ρ为密度，弹性模量为E，μ为泊松比。P为轴向压力。假定径向简谐载荷fr(α,θ,t)=q0cosωbt均匀分布在2ε1×2ε2区域上，中心坐标为(α0，θ0)。

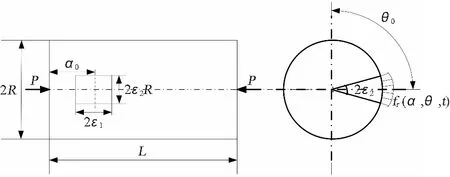
图1 受轴向静力和径向冲击载荷圆柱壳示意图Fig.1 The cylindrical shells subjected to axial compression and impact loads

根据Hamilton原理可以推导出圆柱壳受轴向压力和径向冲击载荷下位移的运动微分方程式如下：

(1)

对于两端简支的圆柱壳，边界条件的表达式为

v=w=Nα=Mα=0,α=0,L。

故可设圆柱壳振动的位移响应为

(2)

将式(2)代入式(1)，并利用轴向静压力作用下圆柱壳的自由振动方程可得：

(3)

式中，ωmnj为自由振动频率。应用振型叠加法，将式(3)两端分别乘Arsjcosrαcossθ，Brsjsinrαsinsθ，Crsjsinrαcossθ， 在圆柱壳边界上积分，然后相加，利用振型正交条件可得如下方程：

(4)

其中：

BmnjsinλαsinnθBrsjsinrαsinsθ+

CmnjsinλαcosnθCrsjsinrαcossθ)Rdαdθ=

解微分方程式(4)可得：

(5)

(6)

将式(6)代入式(2)可计算出壳体的位移，利用式(7)计算出壳体的应变：

(7)

引入无量纲因子：

(8)

2 算例分析

本文以一个圆柱壳受轴向压力和径向冲击载荷的动力响应为例，选取铝质材料。圆柱壳参数E=71 GPa，ρ=2 700 kg/m3，泊松比ν=0.3，h=0.006 m，R=0.105 m，L=2.8 m。圆柱壳轴向压力P=17 320 N，ε1= 0.01×L，ε2= 0.1 π，α0=0.1L，θ0= 0.25 π，q0=10 000 N，ωb=1 000。

利用式(2)和式(7)可计算出本节圆柱壳的位移和应变响应。式(2)右端级数项的取值范围为m=1，2，…M；n=1，2，…N。M，N取不同值时壳体位移的大小如表1所示。

表1给出了m，n取值不同时，壳体位移的收敛情况。由表1可知，以上3种情况位移的误差很小，因而收敛，故在如下计算中，均取m=1～40，n=1～40。

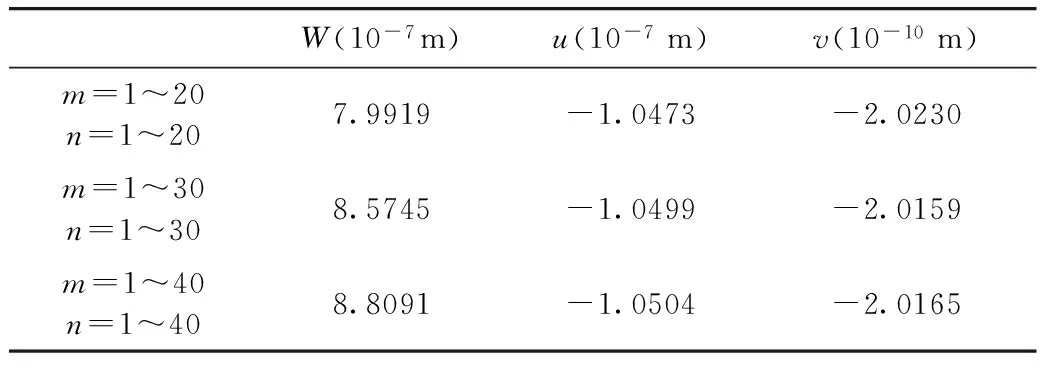
表1 M，N的取值对位移u，v，w的影响

对于力的作用中心点(α0,θ0)处的位移响应和应变响应，计算结果如图2～图10所示。

2.1 位移响应

图2 w～t曲线Fig.2 Curve of w～t

图3 u～t曲线Fig.3 Curve of u～t

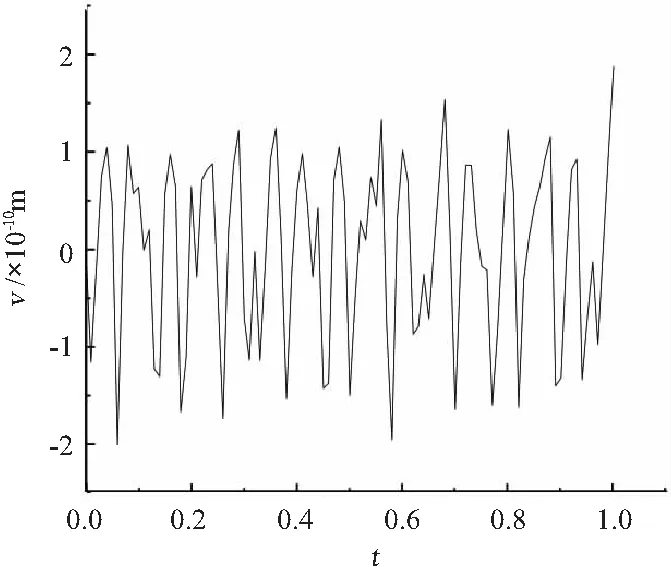
图4 v～t曲线Fig.4 Curve of v～t

图2～图4给出了圆柱壳在3个方向的位移响应。由图可知，壳体在轴向和径向的位移响应远远大于在其周向上的位移响应。

图5和图6给出了t=0.06 s时刻轴向、径向位移的幅频曲线。从图5可以看出：径向位移幅值在Ω2取0.00122，0.01692，0.02，0.09，0.105，0.115，0.25时取得峰值，由式(8)和ω=2πf可知激励频率取285 Hz，1 060 Hz，1 152 Hz，2 444 Hz，2 640 Hz，2 763 Hz，4 074 Hz。同样从图6可看出：Ω2取0.001 22，频率为285 Hz时轴向位移幅值最大。由此可知，径向位移和轴向位移的峰值所对应的频率并不能完全对应起来，激起径向位移峰值的频率并不一定能激起轴向位移取得峰值。

图5 |w|～Ω2Fig.5 Radial displacement response

图6 |u|～Ω2Fig.6 Axial displacement responses

2.2 应变响应

图7 εα～t曲线Fig.7 Curve ofεα～t

图8 |εα|～Ω2Fig.8 Axial strain responses

图9 εθ～t曲线Fig.9 Curve ofεθ～t

图10 |εθ|～Ω2Fig.10 Median strain responses

图7和图9给出了εα和εθ随时间的变化曲线，图8和图10给出了相应的幅频曲线。从图8可看出，Ω2取0.25，频率为4 074 Hz时，εα取值最大。从图10可看出，Ω2取0.47，0.5，0.595，频率为5 586 Hz，5 762 Hz，6 285 Hz时，εθ取最大值。

3 结 语

本文用解析方法，通过数值计算，分析了受轴向静压力和径向冲击载荷作用下圆柱壳的位移和应变响应，得到如下结论：

1)壳体在轴向和径向的位移响应远远大于在其周向上的位移响应。

2)简谐激励频率285Hz,1 060 Hz，1 152 Hz，2 444 Hz，2 640 Hz，2 763 Hz，4 074 Hz时，径向位移取最大值；简谐激励频率为285 Hz时轴向位移取值最大；

3)简谐激励频率为4 074 Hz时轴向应变取得最大值；简谐激励频率为5 586 Hz，5 762 Hz，6 285 Hz时，周向应变取值最大。

[1] LAM K Y，NG Y.Dynamic stability of cylindrical shells subjected to conservative periodic axial loads using different shells theories[J].Journal of Sound and Vibration，1997，207(4) ：497-520.

[2] NG T Y，LAM K Y，LIEW K M.Dynamic stability analysis of functionally graded cylindrical shells under periodic axial loading[J]. International Journal of Solids and Structures，2001，38:1295-1309.

[3] DARABI M，DARVIZEH M，DARVIZEH A.Nonlinear ana-lysis of dynamic stability for functionally graded cylindrical shells under periodic axial loading[J].Composite Structures，2008，83:201-211.

[4] 李学斌，刘土光，朱学康.正交各向性圆柱壳在轴向压力作用下的静动态特性分析[J].舰船科学技术，2004，26:3-8.

LI Xue-bin，LIU Tu-guang，ZHU Xue-kang.Buckling and free vibration study of orthotropic circular cylindrical shell under axial load[J].Ship Science and Technology，2004，26:3-8.

[5] 李学斌.正交各向异性圆柱壳的稳态动力响应分析[J].船舶力学，2007，11(1):79-87.

LI Xue-bin.Harmonic response analysis of or thotropic cylindrical shells[J].Journal of Ship Mechanics，2007，11(1):79-87.

[6] 杨传武，王安稳.冲击载荷作用下超空泡水下航行体的结构响应[J].华中科技大学学报(自然科学版)，2008，36(7):129-132.

YANG Chuan-wu，WANG An-wen.Structural response of supercavitating underwater vehicles subjected to impact loads[J].Journal of Huazhong University of Science and Techndogy(Natural Science Edition)，2008，36(7):129-132.

Dynamical response analysis of cylindrical shells subjected to impact loads

YIN Ping-hua，SUN Chang-jiang

(Bengbu Naval Officer School,Department of Mechanical and Electrical Engineering,Bengbu 233000,China)

The differential equations of motion for cylindrical shells under axial compression and impact loads are derived by use of Hamilton′s theorem，and the analysis solution of the equations have been obtained。The variation curve of the displacement-time and the displacement-frequency have been analyzed by numerical calculation, and also the variation curve of strain-time and strain-frequency have been studied。The numerical calculation results show that the radial displacement response is the greatest when the harmonic response frequency are 285 Hz，1 060 Hz，1 152 Hz，2 444 Hz，2 640 Hz，2 763 Hz，4 074 Hz; The axial displacement response is the greatest when the harmonic response frequency is 285 Hz; The axial strain response is the greatest when the harmonic response frequency is 4 074 Hz; The radial strain response is the greatest when the harmonic response frequency are 5 586 Hz，5 762 Hz，6 285 Hz.

cylindrical shell；impact loads；dynamical response；axial compression

2012-05-15；

2014-04-14

国家自然科学基金资助项目(10772196)

殷平化(1986-)，男，硕士，助理讲师，研究方向为舰艇结构与安全。

O343

A

1672-7649(2014)07-0020-04

10.3404/j.issn.1672-7649.2014.07.004