结合子空间旋转技术的非圆信号快速DOA 估计

王薇，张明，姚博彬，殷勤业，穆鹏程

（1.西京学院信息工程学院，陕西 西安 710123；2.西安交通大学智能网络与网络安全教育部重点实验室，陕西 西安 710049；3.西安微电子技术研究所，陕西 西安 710000；4.长安大学电子与控制工程学院，陕西 西安 710064）

1 引言

波达方向（DOA,direction of arrival）估计作为阵列信号处理的一个重要分支，广泛应用于雷达、声呐、无线通信等领域[1-3]。经典的信号DOA 估计算法有多重信号分类（MUSIC,multiple signal classification）算法、求根 MUSIC（Root-MUSIC,root-multiple signal classification）算法等[4-6]。这些算法都建立在入射信号为窄带或宽带信号的基础上，未考虑入射信号自身的结构特征[6-7]。随着二进制相移键控（BPSK,binary phase shift keying）信号、调幅（AM,amplitude modulation）信号、多进制幅移键控（MASK,multiple amplitude shift keying）信号等非圆信号在实际通信中的应用越来越广泛，众多学者将非圆信号伪协方差矩阵不为零的特点应用于DOA 估计中[7-14]，通过增加阵列接收信号矩阵的维度，扩展阵列的有效孔径，提高DOA 估计的精度。根据非圆信号的特性，文献[9]提出了非圆MUSIC（NC-MUSIC,non-circular MUSIC）算法。该算法具有超高分辨率的优点，但由于引入了二维谱峰搜索，算法运算量庞大，工程实用性大打折扣。为了降低NC-MUSIC 算法的运算复杂度，文献[9]又提出了非圆Root-MUSIC 算法，利用多项式求根代替二维谱峰搜索，在一定程度上降低了NC-MUSIC 算法的运算复杂度。文献[10-11]采用凸优化方法将NC-MUSIC 算法中的二维谱峰搜索转化为一维谱峰搜索，大幅降低了谱峰搜索阶段的运算量，但其一维谱峰搜索仍具有较高的运算复杂度。文献[12-13]通过欧拉变换将复数据转化为实数据，并在构建空域字典集的基础上，通过稀疏重构实现DOA 估计。该算法虽可降低DOA 估计的运算复杂度，但前提是要精确补偿由传输时延带来的非圆相位，且信号入射角度需精确位于字典网格上。当实际环境不满足前提要求时，算法的估计性能会严重下降。

为了降低非圆信号NC-MUSIC 算法的运算复杂度，本文提出一种结合子空间旋转的非圆信号快速DOA 估计算法。所提算法结合子空间旋转技术（SRT,subspace rotation technique）[14]，通过对信号噪声子空间的旋转获得降维噪声子空间；所构造的降维噪声子空间与扩展后阵列流型矩阵张成的空间具有正交性，利用该正交性和变量分离可将NC-MUSIC 算法的二维谱峰搜索转化为一维谱峰搜索。所提算法在保持DOA 估计性能的基础上，可将算法运算复杂度降至NC-MUSIC 算法运算复杂度的5%以下；对于大阵元情况，所提算法的计算效率提升明显。

2 数据模型及非圆信号的NC-MUSIC 算法

2.1 数据模型

非圆信号是现代通信系统中的一种常见信号，其具有伪协方差不为0 的特征，即E{S2(t)}≠0（S(t)为非圆信号）。利用这一特征可通过增加虚拟阵元的个数，扩展阵列的有效孔径。常见的BPSK 信号、AM 信号、MASK 信号等非圆信号的非圆率均为1。对于最大非圆率（即非圆率为1）信号，由于理想情况下其经过解调后所得信号为实信号，考虑实际中传输信道对信号的影响，经解调后的信号模型为S(t)=SR(t)ejϕ，其中，SR(t)为实信号，ϕ为信号初相与传输信道附加相位之和[7-13]。假设有K个互不相关的窄带最大非圆率信号S1(t),S2(t),…,SK(t)分别以方向θ1,θ2,…,θK同时入射至一个M元均匀线阵，阵列阵元间距为d，阵列中的天线均为全向天线，天线增益均为单位增益。均匀线阵阵列结构如图1 所示。

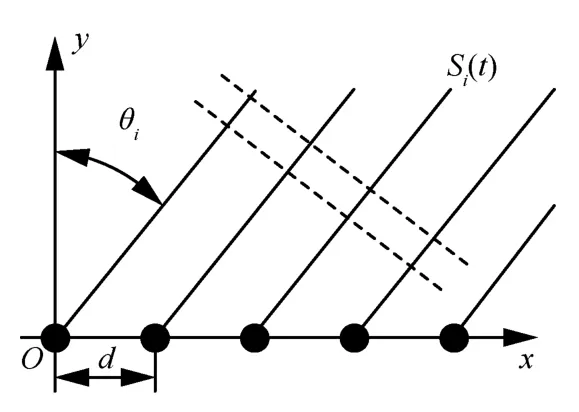
图1 均匀线阵阵列结构

选定最左侧阵元为参考阵元，则该均匀线阵的接收信号可以表示为

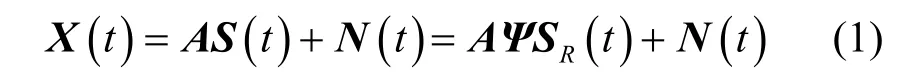
其中，信源矢量S(t)=[S1(t),S2(t),…,SK(t)]T∈CK×1，；阵列流型矩阵A=[a(θ1),a(θ2),…,a(θK)]∈CM×K，导向矢量，λ为信号载波波长；，ϕk(k=1,2,…,K)为第k个窄带非圆信号的非圆相位；加性高斯白噪声矢量。

由于非圆信号具有E{S(t)ST(t)}≠0 和E{S*(t)SH(t)}≠0 的性质，故可将接收信号X(t)与其共轭X＊(t)串联，通过重构接收信号矩阵来增加可利用的阵元个数[10-15]。重构后的接收信号Y(t)为

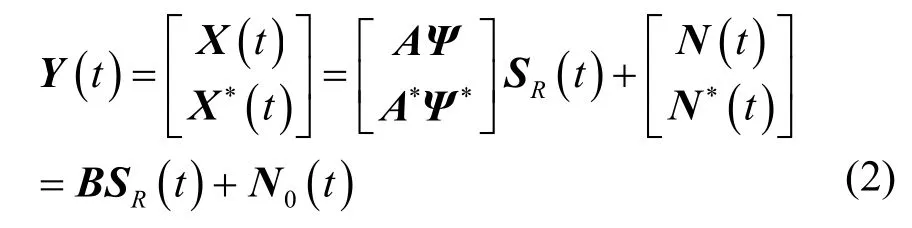
其中，B和N0(t)分别为

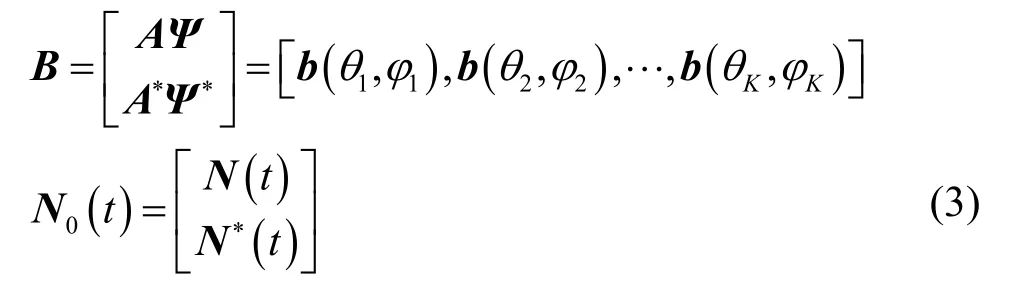
2.2 非圆信号的MUSIC 算法

重构后的接收信号的协方差矩阵为

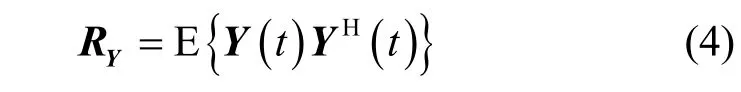
实际应用中通常采用接收信号X(t)的L次快拍X(n) (n=1,2,…,L)估计协方差矩阵RY，即

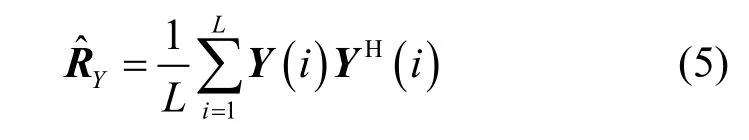
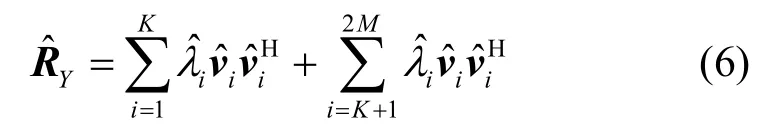
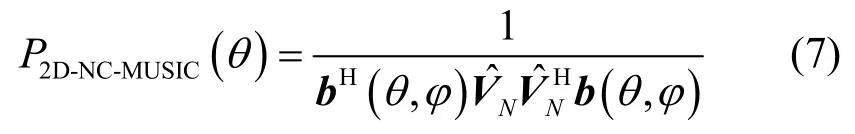
其中，

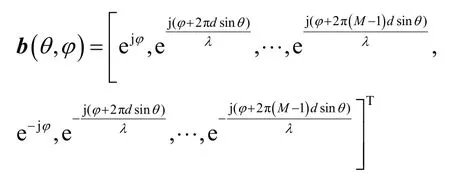
对式(7)所示的空间谱函数关于入射角θ和非圆相位ϕ进行二维谱峰搜索，所得K个极大值对应的入射角θ即为信号的DOA。NC-MUSIC 算法通过虚拟阵列的方法扩大了阵列的有效孔径[10-11]，极大地提高了DOA 估计的空间分辨率；同时，烦琐的二维谱峰搜索带来了极高的运算复杂度，约束了其在实际工程中的应用。

3 结合SRT 的SRTRD-NC-MUSIC 算法

NC-MUSIC 算法利用非圆信号伪协方差矩阵不为零的特性重构接收信号的协方差矩阵，根据信号子空间和噪声子空间的正交性构造二维空间谱函数估计非圆信号的DOA。该算法以增加虚拟阵元的方法提高了DOA 估计的精度，同时也带来了烦琐的二维谱峰搜索[11-12]。本文所提算法——SRTRD-NC-MUSIC 算法以降低非圆信号NC-MUSIC 算法的运算复杂度为目标，结合SRT 实现快速估计非圆信号DOA。SRTRD-NC-MUSIC 算法分为2 个步骤：首先，对噪声子空间矩阵按行分块，利用SRT 构造降维噪声子空间；然后，根据所构造的降维噪声子空间与扩展后阵列流型矩阵张成空间的正交性，结合变量分离把NC-MUSIC 算法的二维谱峰搜索转化为一维谱峰搜索。SRTRD-NC-MUSIC 算法在将二维谱峰搜索转化为一维谱峰搜索的同时，通过构造降维噪声子空间有效避免了一维谱峰搜索中的冗余计算。

3.1 子空间旋转及重构噪声子空间

对2M×(2M−K)维的噪声子空间进行分块处理，可得

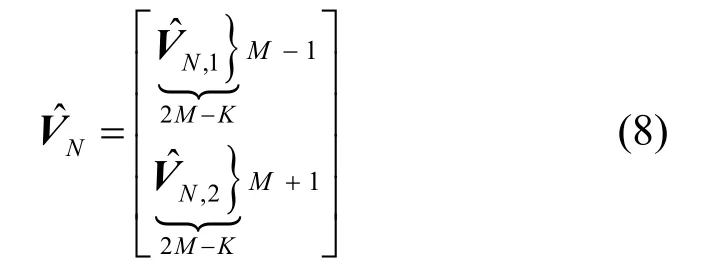
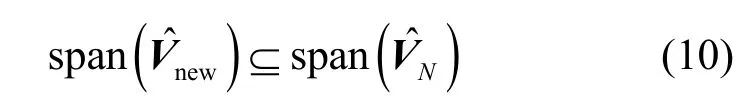
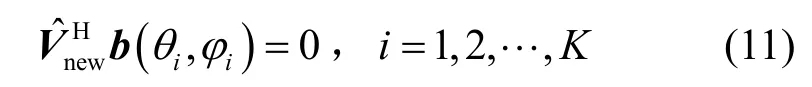
3.2 构造降维空间谱函数

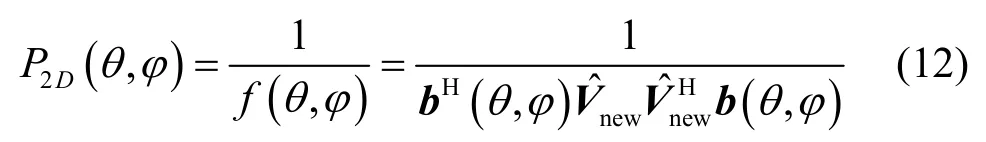
通过搜索f(θ,ϕ)的极小值，即可获得信号DOA 的估计。将b(θ,ϕ)按式(13)进行变量分离，即

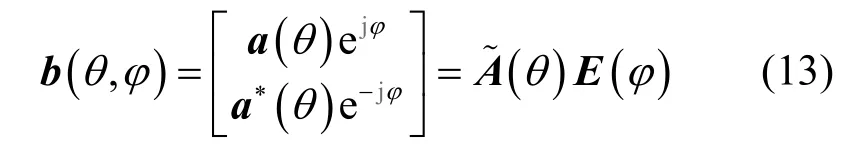
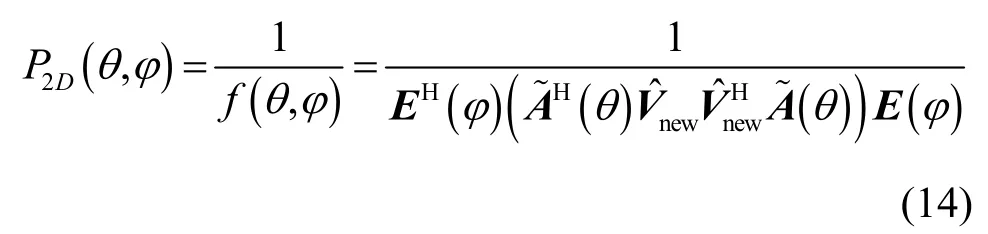
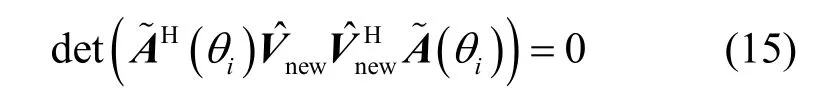
因此，可构造出新的一维空间谱函数为

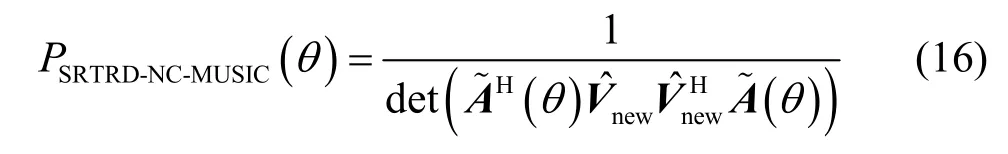
对式(16)构造的空间谱函数进行谱峰搜索，所得K个极大值对应的角度θ即为信号DOA 的估计。与NC-MUSIC 算法相比，SRTRD-NC-MUSIC 算法通过旋转噪声子空间降低了噪声子空间的维数，且只需进行一维谱峰搜索即可估计信号DOA。后文分析将表明，SRTRD-NC-MUSIC 算法可以在保证DOA 估计精度的前提下，降低NC-MUSIC 算法的运算复杂度，大幅提升计算效率。

3.3 SRTRD-NC-MUSIC 算法化简

将式(8)代入式(9)，可得

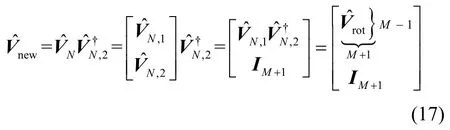
对2×2M维矩阵按式(18)进行划分，即

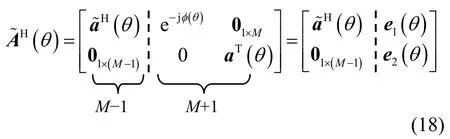
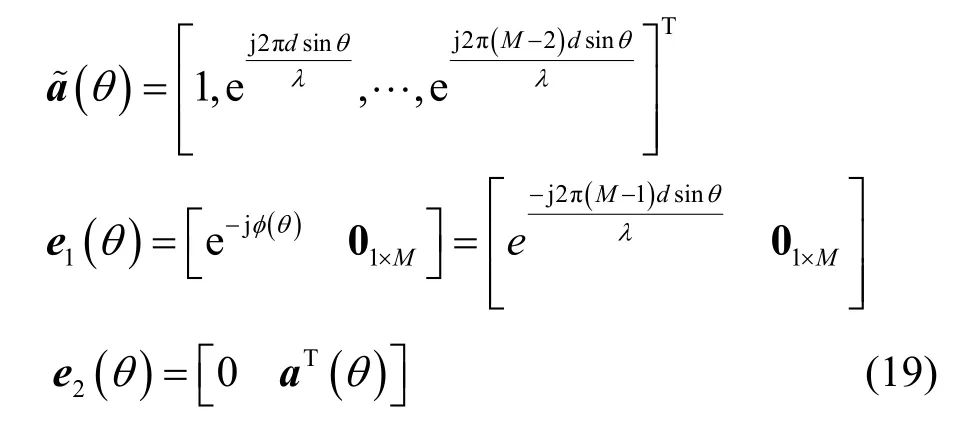
将式(19)代入式(17)和式(18)，可得

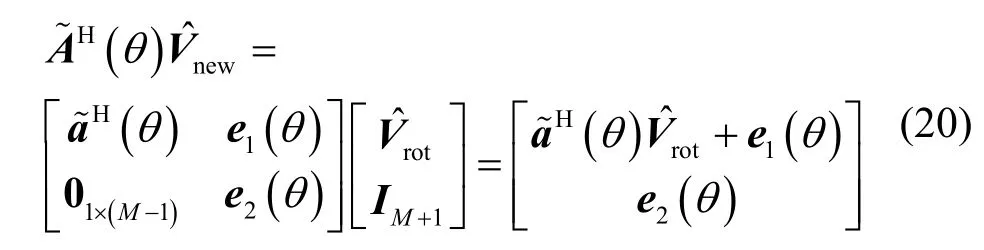
进一步将式(20)代入式(16)，并省略式中角度θ的标记，可得

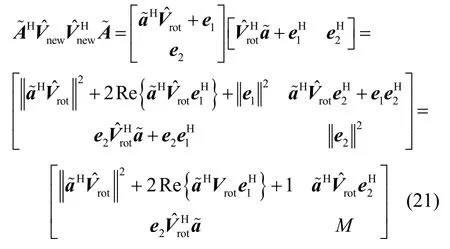
因此，SRTRD-NC-MUSIC 算法可化简为

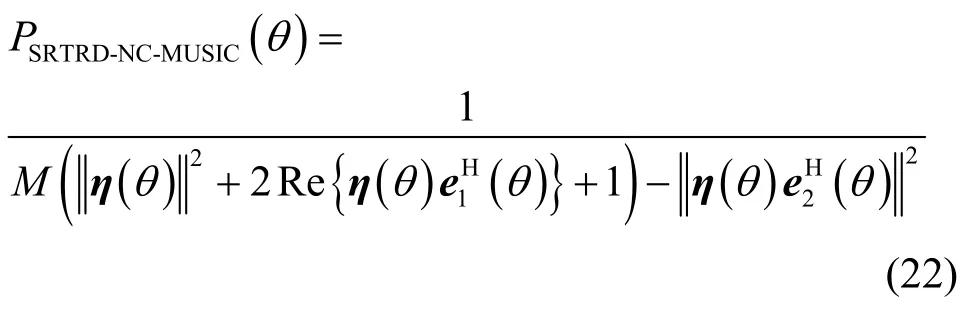
对比式(7)和式(22)可得，SRTRD-NC-MUSIC算法不仅将NC-MUSIC 算法中的二维谱峰搜索转化为一维谱峰搜索，而且通过矩阵分块和子空间旋转，有效降低了噪声子空间的维数，进一步去除了一维谱峰搜索中的冗余计算。

3.4 运算复杂度分析

本文采用复数乘法的数量来衡量算法的运算复杂度[12-14]。NC-MUSIC 算法和 SRTRD-NCMUSIC 算法均包含对协方差矩阵的特征值分解。根据文献[18]所提的快速子空间分解法可得，矩阵进行特征值分解的运算复杂度为O(4M2K)。对比NC-MUSIC 算法和SRTRD-NC-MUSIC 算法可知，SRTRD-NC-MUSIC 算法需额外构造新噪声子空间和计算。已知为2M×(2M−K)维矩阵，为(M+1)×(2M−K)维矩阵，故构造所需的运算复杂度为O[(M−1)(M+1)(2M−K)]+O[2M(2M−K)][14]。

NC-MUSIC 算法和SRTRD-NC-MUSIC 算法均包含谱峰搜索过程。在谱峰搜索阶段，NC-MUSIC算法需同时对入射角θ和非圆相位ϕ进行二维谱峰搜索。假设在角度搜索范围和[0,2π]非圆相位搜索范围内总的搜索角度数均为J，则NC-MUSIC 算法完成谱峰搜索所需的运算复杂度为O[J2(2M+1)(2M−K)]。根据SRTRD-NC-MUSIC 算法的式(22)进行谱峰搜索时，计算的运算复杂度为O[M(M+1)]，计算的运算复杂度为O(M)，计算的运算复杂度为O(M2+1)，则SRTRD-NC-MUSIC 算法完成谱峰搜索所需的运算复杂度为O[J(2M2+2M+1)]。

综上，NC-MUSIC 算法和SRTRD-NC-MUSIC算法总的运算复杂度分别为

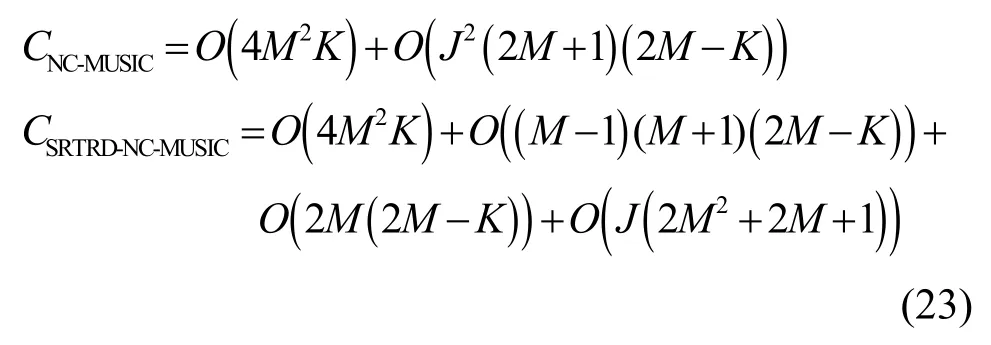
实际中，通常有J≫M＞K，故可将式(24)近似为

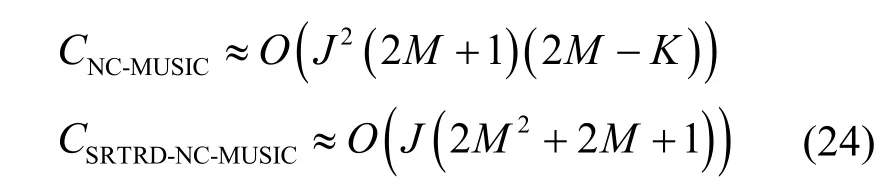
图2 对比了不同阵元数和信源数下NC-MUSIC算法、RD-NC-MUSIC 算法[11]和 SRTRD-NCMUSIC 算法的运算复杂度。图2 中，总搜索角度数J=1 000。RD-NC-MUSIC 算法的运算复杂度为[11]。可见，3 种算法的运算复杂度都随着阵元数增加而增大。与NC-MUSIC 算法相比，SRTRD-NC-MUSIC 算法大幅降低了算法运算复杂度，尤其是在阵元数目较多的情况下，SRTRD-NC-MUSIC 算法的计算效率优势更明显；同时，SRTRD-NC-MUSIC 算法的运算量仅为RD-NC-MUSIC 算法的运算量的25%左右。

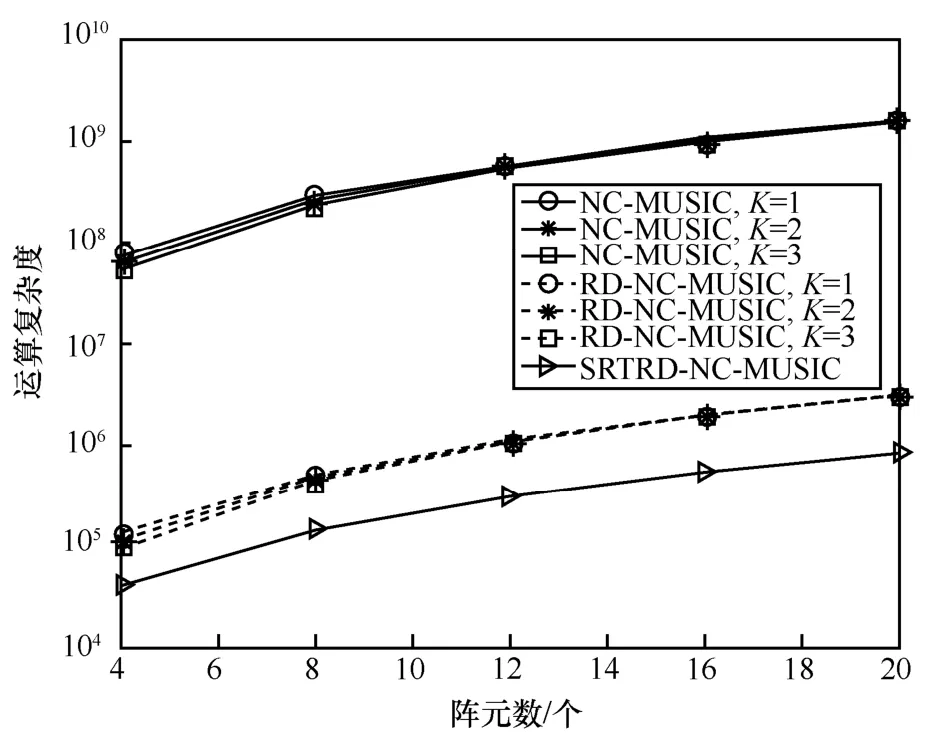
图2 不同算法运算复杂度与阵元数M 和信源数K 之间的关系

3.5 算法实施步骤

根据上述分析可得，SRTRD-NC-MUSIC 算法的具体实施步骤如下。

步骤1根据阵列接收信号X(t)的L次快拍X(n)(n=1,2,…,L)和式(2)重构接收矩阵Y(n)。

步骤2按照式(5)计算重构后接收信号协方差矩阵的估计，并根据式(6)对进行特征值分解，获得噪声子空间。

步骤3根据式(8)对进行分块处理，同时根据式(9)和式(18)分别构造新的噪声子空间和矩阵。

步骤4根据式(22)构造一维空间谱函数PSRTRD-NC-MUSIC(θ)。

步骤5确定步骤4 中PSRTRD-NC-MUSIC(θ)的R个极大值，这R个极大值对应的角度即为入射信号DOA 的估计。

4 仿真结果与分析

下面通过计算机仿真验证SRTRD-NC-MUSIC 算法的有效性，并与NC-MUSIC 算法、RD-NC-MUSIC算法进行比较分析。实验中接收阵列采用均匀线阵（其中，图3～图7 的阵元数目均固定为8），阵元间距d=0.5λ，入射信号为等功率的窄带BPSK 信号，噪声为加性高斯白噪声。各实验结果均采用3 000次蒙特卡罗实验的统计平均。定义均方根误差（RMSE,root mean square error）为

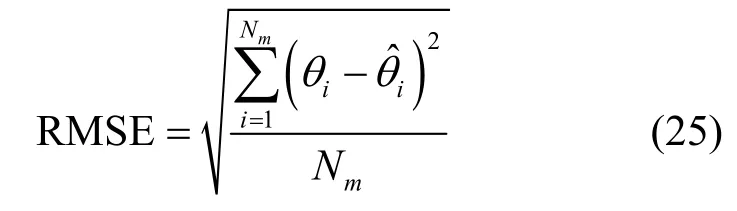
其中，θi和分别为信号入射角的真实值和估计值，Nm为蒙特卡罗仿真的次数。对于来波方向相近的2 个信号，如果满足

即认为成功分辨2 个入射信号。其中，θ1和θ2分别为2 个信号的来波方向，P(·)为空间谱函数。

图3给出了SRTRD-NC-MUSIC算法和NC-MUSIC算法的DOA 估计效果。选定信号入射角分别为−40°、−20°和10°，信噪比（SNR,signal-to-noise ratio）为 5 dB，快拍数为 1 000。由图 3 可看出，SRTRD-NC-MUSIC 算法可以准确有效地估计出入射信号的 DOA。与 NC-MUSIC 算法相比，SRTRD-NC-MUSIC 算法估计的空间谱峰更尖锐，两者估计精度基本一致；同时，SRTRD-NC-MUSIC算法的运算复杂度快速减小，计算效率显著提升。

选定信号入射角分别为−20°和15°，图4 和图5分别给出了SRTRD-NC-MUSIC 算法、NC-MUSIC算法和RD-NC-MUSIC 算法的估计误差随信噪比和快拍数的变化对比。图4 固定快拍数为500，图5固定信噪比为10 dB。从图4 可以看出，3 种算法的估计误差均随信源信噪比的增加而减小；同时，由于SRTRD-NC-MUSIC 算法将NC-MUSIC 算法中的二维谱峰搜索转化为一维谱峰搜索，故其估计性能较NC-MUSIC 算法略差，但整体较接近NC-MUSIC算法的估计性能，且优于RD-NC-MUSIC 算法的估计性能。由图5 可得，随着快拍数的增加，重构后的接收信号的协方差矩阵可更加精确地估计，故3 种算法的估计误差都有所减小；且SRTRD-NC-MUSIC 算法的估计性能更接近NC-MUSIC 算法的估计性能。由此可见，SRTRD-NC-MUSIC 算法计算效率的提高并未以过大地牺牲估计精度的方式换取。

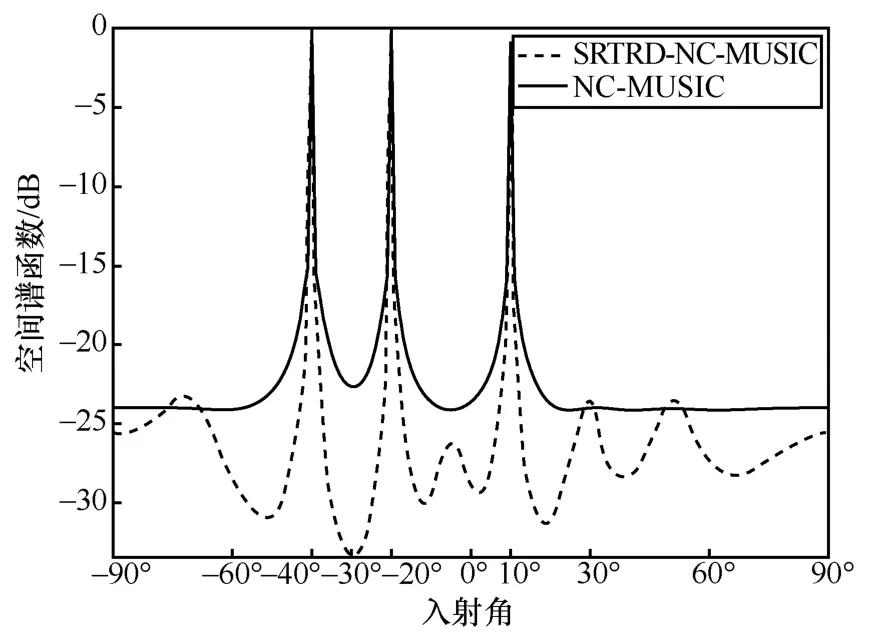
图3 SNR=5 dB 时SRTRD-NC-MUSIC 算法和NC-MUSIC 算法的DOA估计效果

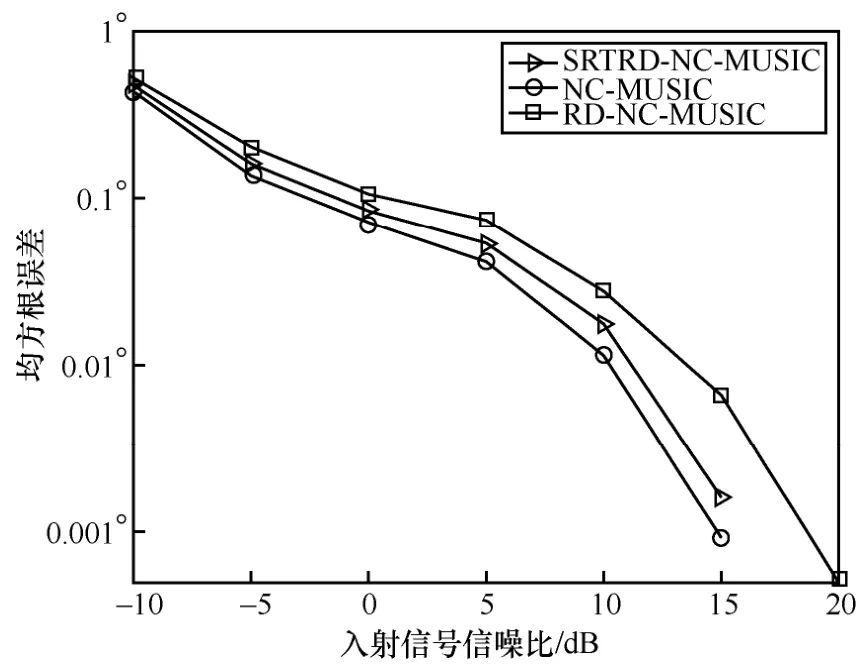
图4 不同算法的估计误差与信噪比的关系

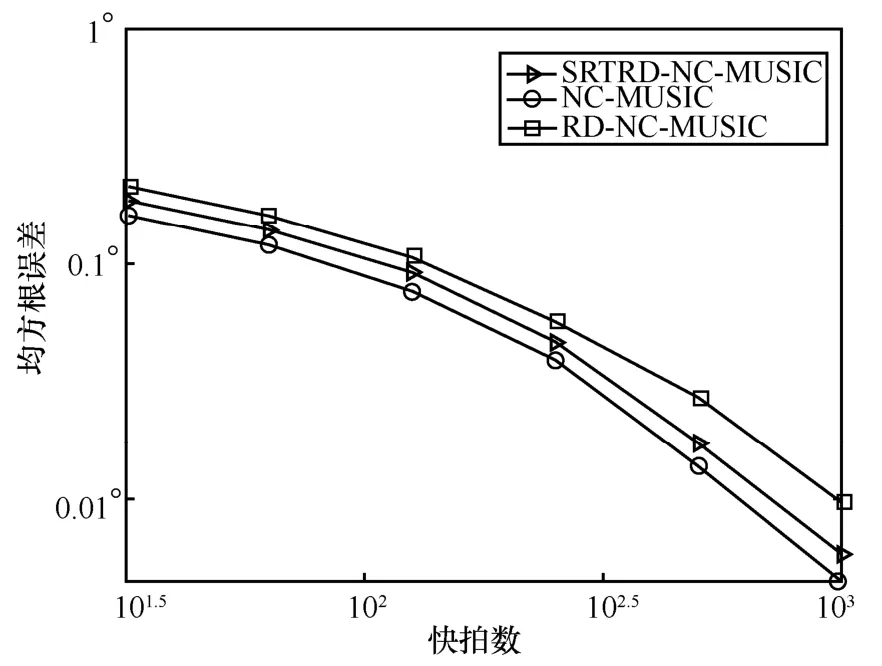
图5 不同算法的估计误差与快拍数的关系

图6 和图7 的信号入射角均分别固定为18°和20°，快拍数为500。图6 对比了不同信噪比下SRTRD-NC-MUSIC 算法、NC-MUSIC 算法和RD-NC-MUSIC 算法成功分辨出2 个靠近目标的概率。由图6 可见，在低信噪比（SNR＜0）情况下，SRTRD-NC-MUSIC 算法的分辨成功率明显高于NC-MUSIC 算法和RD-NC-MUSIC 算法，这是因为SRTRD-NC-MUSIC 算法通过构造降维噪声子空间改善了信号子空间与噪声子空间的正交性，且降维噪声子空间的维度下降，使其空间谱变得更尖锐。故相比于其他2 种算法，SRTRD-NC-MUSIC 算法分辨2个靠近目标的能力更强。图7给出了SNR=5 dB时SRTRD-NC-MUSIC 算法与NC-MUSIC 算法的10 次叠加空间谱。由图7 可得，SRTRD-NC-MUSIC算法估计的空间谱峰比NC-MUSIC 算法更尖锐，分辨相近来波方向上信号的能力更强，验证了图6 的实验结果。

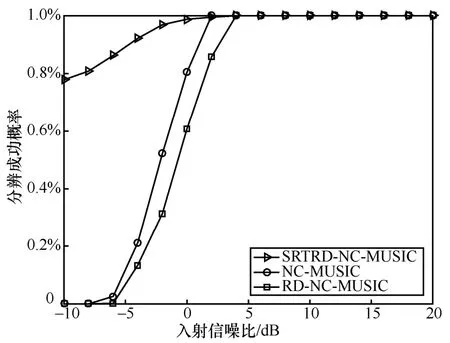
图6 不同算法的分辨成功概率与信噪比的关系

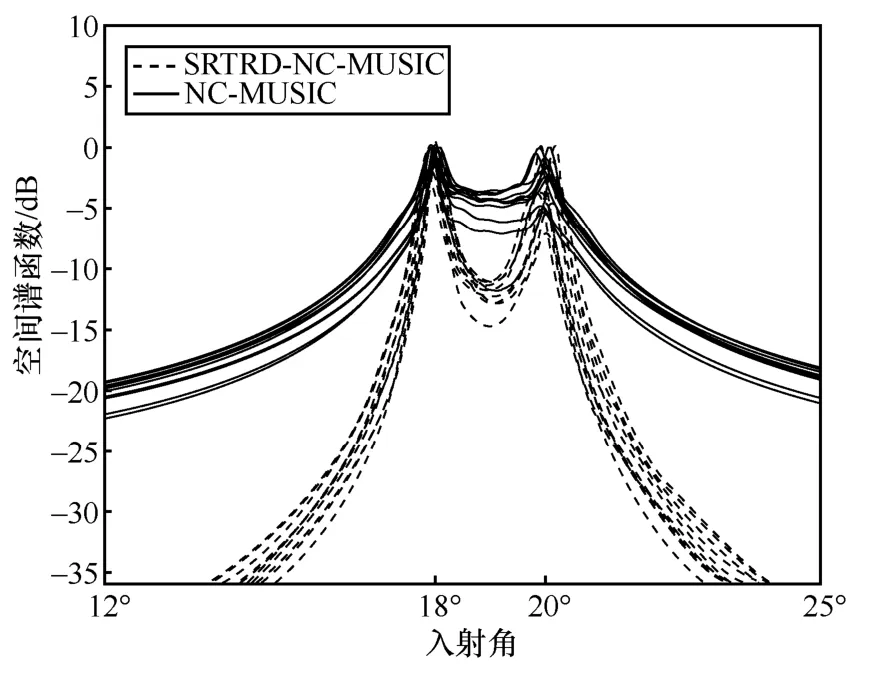
图7 SRTRD-NC-MUSIC 算法与NC-MUSIC 算法的叠加空间谱

图8 对比了不同阵元数目下采用SRTRD-NCMUSIC 算法、NC-MUSIC 算法和RD-NC-MUSIC算法完成DOA 估计的计算机时间开销。图8(a)为SRTRD-NC-MUSIC 算法与NC-MUSIC 算法的仿真时间对比，图8(b)为SRTRD-NC-MUSIC 算法与RD-NC-MUSIC 算法的仿真时间对比。选取信号入射角分别为−10°和30°，角度搜索间隔为0.05°，SNR=10 dB，快拍数为500。以Intel(R) Core(TM)i5-5300U 处理器，2.3 GHz CPU，4 GB 内存的PC平台运行3 种算法的MATLAB 程序。由图8 可看出，SRTRD-NC-MUSIC 算法的计算机时间开销显著小于其他2 种算法。同时，3 种算法的时间开销均随阵元数增加而增大；SRTRD-NC-MUSIC 算法的计算效率优势随阵元数增加更明显。这与上文运算复杂度分析部分的现象一致。图8(a)中，由于SRTRD-NC-MUSIC 算法将NC-MUSIC 算法的二维谱峰搜索转化为一维谱峰搜索，且利用噪声子空间的秩亏特性，通过构造降维噪声子空间避免了一维谱峰搜索中的冗余计算，故SRTRD-NC-MUSIC 算法可将算法复杂度降低至NC-MUSIC 算法运算复杂度的5%以下。图8(b)中，与RD-NC-MUSIC 算法相比，SRTRD-NC-MUSIC 算法构造的降维噪声子空间维度下降，去除了一维谱峰搜索中的冗余计算，故SRTRD-NC-MUSIC 算法可将算法复杂度降低至RD-NC-MUSIC 算法运算复杂度的25%以下，大幅提高算法的计算效率。

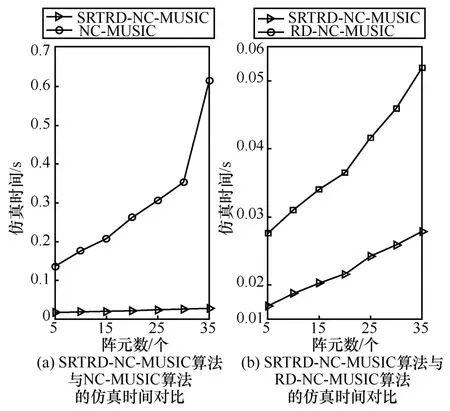
图8 不同算法的计算机时间开销与阵元数的关系

5 结束语

本文以降低非圆信号NC-MUSIC 算法的运算复杂度为目标，提出了一种结合子空间旋转的非圆信号快速DOA 估计算法。SRTRD-NC-MUSIC 算法对噪声子空间按行分块，并通过子空间旋转的方法构造降维噪声子空间；在将二维谱峰搜索转化为一维谱峰搜索的同时，利用降维噪声子空间有效避免了一维谱峰搜索中的冗余计算。通过实验仿真和运算复杂度分析可以看出，SRTRD-NC-MUSIC 算法能够在保持 DOA 估计性能的前提下大幅降低NC-MUSIC 算法的运算复杂度，显著提高算法的计算效率；特别是在阵元孔径较大的场景下，SRTRDNC-MUSIC 算法计算效率提升更明显。