Material Selection for Hawsers for a Side-by-side Offloading System
2014-07-30JiayuQianLipingSunandLinfengSong
Jiayu Qian, Liping Sun and Linfeng Song
Deep Water Engineering Research Center, Harbin Engineering University, Harbin 150001, China
1 Introduction1
Floating production, storage and offloading (FPSO) has become a popular solution for exploitation activities concerning ocean oil and gas resources throughout the world.As a part of the marine oil and gas development system, it generally comes with a shutter tanker and subsea production unit consisting of a complete production system. The FPSO offloading system is a type of transmission form, which transfers crude oil and natural gas from the FPSO to the shuttle tanker by a marine hose or offloading arm directly.
The MingZhu FPSO side-by-side offloading system in the field BZ25-1 is presented here. Several types of ropes can be used to connect the FPSO to the tanker; four fenders are set between the vessels to prevent collisions. Especially, the FPSO is moored by a yoke system. Four different types of ropes with strong viscoelasticity characteristics, such as polyester and nylon, are analyzed in this work. The properties of the stress-strain relationship of the fiber ropes within the elastic range are mainly shown as nonlinear. Due to the strong nonlinearity of the axial stiffness, many scholars (Websteret al., 2012) have carried out the relevant research regarding the effects of the synthetic rope materials on the floating structure dynamics.
Del Vecchio and Chaplin (1992) applied fiber rope in a deep water mooring system which indicated that high-strength material could reduce the line dynamic tension under wave excitation forces. A two-dimensional calculation was performed to estimate the stress-strain relationship of the fiber rope accurately by Liuet al. (1997). The exponential function can be expressed by the load-strain relationship of the fiber rope through model test analysis(Mc Kenna and Wong, 1979). The elastic modulus of the long-period formula (Fernandeset al., 1998) was utilized to calculate the fiber line tension; and Kimet al. (2003)applied it to the spar platform. The empirical formula(Bosman and Hooker, 1999) was applied to calculate the fiber line tension of a spar mooring system (Tahar and Kim,2008). Davieset al. (2008) studied the influence of the fiber stiffness on the deepwater mooring line response. Yuanet al.(2010) compared the performance of the mooring system for a spar platform with a linear and nonlinear elastic model to fit the stress-strain relationship of the fiber rope, respectively.The results of the spar platform with the nonlinear elastic model are different from the ones using the linear elastic model. Kimet al. (2011) applied a viscoelastic model considering multiple relaxation times and nonlinearity in dynamic stiffness into a spar platform. Taharet al. (2012)presented the global performance comparison between the dual stiffness method and the traditional method when using polyester mooring lines. The above research and the reference (Qianet al., 2013) indicate that it is important to use a nonlinear mathematical model of fiber ropes in terms of analyzing the dynamic responses of the floating structures.
According to the researches mentioned above, the dynamic time-domain coupled method is discussed here to study the impact of using different types of hawser materials on the FPSO offloading system. The most suitable hawser material for the FPSO offloading system is chosen through comparing the relative motion of two vessels and the hawser line tension. To obtain the accurate hawser line tension, a polynomial function is applied here to simulate the nonlinear stress-strain relationship of the lines. Especially,as for the polyester rope, this paper uses lower and upper bound linear stiffness to calculate the line tension, and the results agree well with the results of the nonlinear stiffness.Then the polynomial fitting method used to calculate the nonlinear stiffness of the fiber ropes is verified.
2 Mathematical formulations
The 3D potential flow theory is used to calculate the hydrodynamic interaction coefficients of the multi-body in the limited frequency range. And then the coefficients including the added mass, damping and second-order transfer function matrix are prepared for solving the motion equations of the vessels in the time-domain simulation. To adopt the accurate dynamic response of the offloading system, a polynomial function is made in the application to fit the rope stiffness. Different types of fiber ropes have different stiffness characteristics. This paper focuses on selecting the most suitable fiber rope for FPSO offloading systems through a series of calculations.
2.1 Equations of motion for mutual floating bodies
Floating structures contend with wind force, hydrostatic restoring force, wave radiation/diffraction force, gravity,inertia force and flow force from wind, waves and currents.The assumption is made that there arenfloating bodies,considering the mutual interference between the floating bodies. According to Newton’s second law, the 6×ndegree of freedom time-domain coupled equation (Songet al., 2013)of the bodies under the environmental load is as follows:
whereMmis the mass matrix of floating bodym,m=1,…,n;ukjis the added mass matrix of floating bodym, including itself and mutual interference;bkjis the impulse response function in the time-domain of the floating bodym,including itself and mutual interference;Ckjis the hydrostatic restoring force coefficient with the interaction of thekandjmotion modes of the floating body,k=1,…,6;ηjrepresents thejmotion mode of the floating body,j=1,…,6;Fmrepresents the floating bodymsubjected to an external load.
2.2 Calculation of the nonlinear stiffness of fiber ropes
Because the fiber rope belongs to the viscoelastic material, the global behavior of the stress-strain curve for the fiber rope was nonlinear. According to the guidance(Bridon, 2007), Fig. 1 plots the relationship between the load and extension of the four kinds of fiber ropes.
Nylon A and nylon B belong to the high-tenacity nylon multifilament fiber. Polyester M and polyester N represent worked and new braidlines, which are part of the high-tenacity polyester rope.
There are no specific nonlinear stiffness values of these ropes. So it is necessary to use a mathematical formula to fit the load-extension curves of the ropes. This paper uses the polynomial function to fit the curves and then obtains the corresponding nonlinear stiffness values. The equations for calculating the fiber rope nonlinear stiffness are as follows:
whereEAis the line elastic modulus;k1,k2andk3are the coefficients of the polynomial function and they are constants;εrepresents the line strain.
Fig. 1 The load-extension relationship of the fiber ropes
2.3 Environment condition
The frequency range of the FPSO and tanker is chosen from 0.1 to 1.7 rad/s; the working depth is 17.4 m. The irregular waves are generated using the JONSWAP spectra;the significant wave height is 3.2 m, and the wave period is 7.9 s. The unsteady current velocity is 1.34 m/s. The one-hour average wind speed is 18 m/s. The incident angle of the wind, waves and current are all from the FPSO bow pointing stern. The dynamic response is recorded in the duration of three hours and the time interval is 0.1 s. The wind and current loads are directly proportional to the square of the corresponding speed, and the equation is as follows to calculate the environment loads on the hull:

whereFjrepresents the wind force or current force in thejdirection;Vthe average wind speed or current speed, which exist at a certain distance from the static water;Cjthe wind or current coefficient in thejdirection, which accords with OCIMF (1994) specification; andAthe hull wind area or hull current area.
3 Numerical models
The FPSO offloading system consists of five parts,including the FPSO, offloading hawsers, shutter tanker, soft yoke system and fenders. The universal joints connect the soft yoke and mooring structure, and the tube unit is used here to simulate the yoke system. The stress-strain relationship of the hawser line is nonlinear. And the hawser line tension is zero when it is slack. Similarly, the stress-strain relationship of the fenders is also nonlinear.
3.1 The model of the FPSO and tanker
The yoke mooring system is used to position the FPSO with a mooring force of 410 tons. The working depth of the FPSO offloading system is 17.4 m. In order to prevent the FPSO and shuttle tanker from colliding, there are four fenders between the two vessels to absorb energy. The fenders are modeled as springs, which are kept on the water surface at all times. The diameter of the fender is 2.5 m and the length is 5.5 m. Each fender can absorb 211 kN·m when they are 60% shaped. The specific performance parameters of the fenders can be seen with the reference (Sunet al.,2011). The main parameters of the FPSO and shuttle tanker are shown in Table 1. The distribution of the surface mesh of the two vessels is shown in Fig. 2.
Item FPSO Tanker Length overall/m 218.3 180 LBP/m 210 171.2 Breadth/m 32.8 32.2 Depth/m 18.2 14.2 Draft/m 11.7 5.43 Displacement/t 75 501.5 24 216.9 Gx /m 100.775 86.157 Gz /m 12.248 8.71 Wind area (frontal)/m2 541.2 604.4 Wind area (side)/m2 2 619 1 689.6
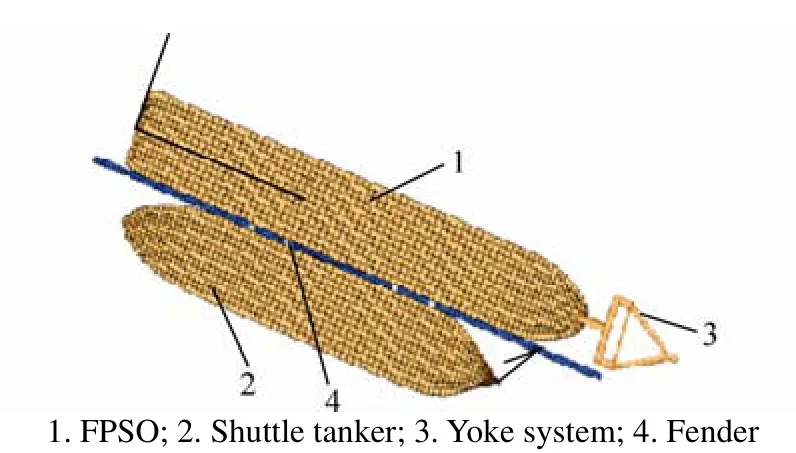
Fig. 2 FPSO offloading system
3.2 The hawser line
There are ten hawser lines between the FPSO and shutter Tanker. Four lines are set in the bow and stern of the FPSO and shuttle tanker. And two lines are set across each other in the middle of the two vessels. To prevent the hawser line from being damaged, the pretension will be controlled within the range of 30% breaking strength (American Petroleum Institute, 2001; Wanget al., 2010) and applied to each hawser to provide the initial stiffness.
The most suitable fiber rope will be chosen by analyzing the dynamic response of the FPSO offloading system when the hawser uses types of fiber ropes with different characteristics. The diameter of the fiber ropes is 120 mm.The wet weight and minimum breaking strength (MBS) of the polyester rope are 2.79 kg/m and 2 697 kN, respectively.The wet weight and minimum breaking strength of the nylon are 0.86 kg/m and 3 246 kN, respectively.
The specific arrangement of the hawsers is shown in Fig. 3.Table 2 illustrates the positions of the hawser ropes in the FPSO and tanker.

Table 2 The position of hawsers in the FPSO and tanker
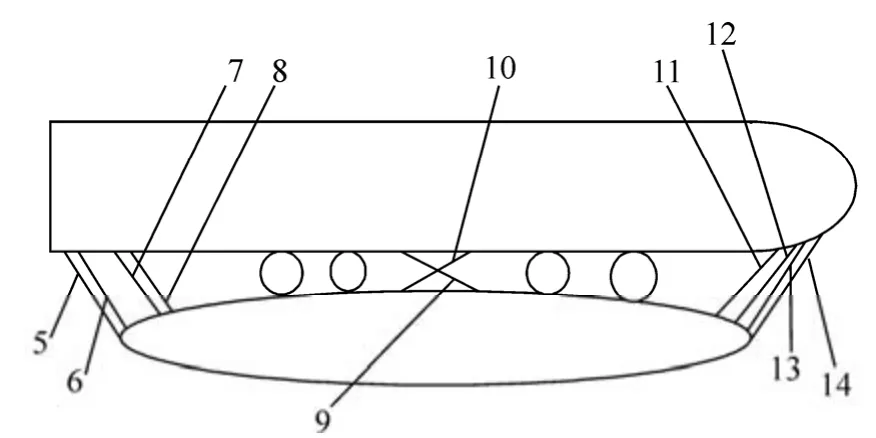
Fig. 3 The arrangement of hawser lines
4 Simulation and discussion
The hydrodynamic coefficients of the mutual influence between the FPSO and tanker can be acquired based on the 3D potential flow theory, and then the corresponding wave forces can be obtained. It may produce abnormal values in the hydrodynamic coupled analysis. This paper uses a rigid lid between the two vessels to suppress the abnormal values,which can be seen in these references (Buchneret al., 2001;Newman, 2004). In order to get a more accurate slow drift force, the near-field integral method is utilized here.
4.1 The relative motion of the FPSO and shuttle tanker
As for the four different types of fiber ropes, considering the interaction of the FPSO, soft yoke, tanker and the hawser lines, the dynamic response of the system can be required through time-domain simulation. This paper utilizes the root mean square (RMS) to estimate the relative motion amplitude of the two vessels. The relative motion results with different materials can be seen in Table 3. Figs. 4–6 present the relative surge, sway and heave motion of the FPSO and tanker, respectively.
The polyester N material reaches the smallest response amplitude in the vertical relative motion of the two vessels.Taking #5 fairlead as an example, the surge RMS of the polyester N material is 0.221 7, which is less than the numbers of the polyester M, nylon A and nylon B material by 69.0%, 23.0% and 6.6%, respectively. The results illustrate that the external load has a small effect on the line elongation,and it would be more beneficial to the vessel stability in the longitudinal direction. In the lateral direction, using polyester N and nylon B will allow for the smaller relative motion of sway of the two vessels than the polyester M and nylon A material. The results indicate that the stiffness characteristic of the fiber rope has a large effect on the relative sway motion of the vessels when the external load is greater than 11% MBS. Generally, polyester N has the smaller impact on the relative heave motion of the vessels because it has larger stiffness and a bigger curvature of the load-extension relationship. For example, the heave RMS value of polyester N is 0.245 9 in the #12 fairlead, which is less than the numbers of the polyester M, nylon A and nylon B material by 20.9%, 0.2% and 7.6%, respectively.
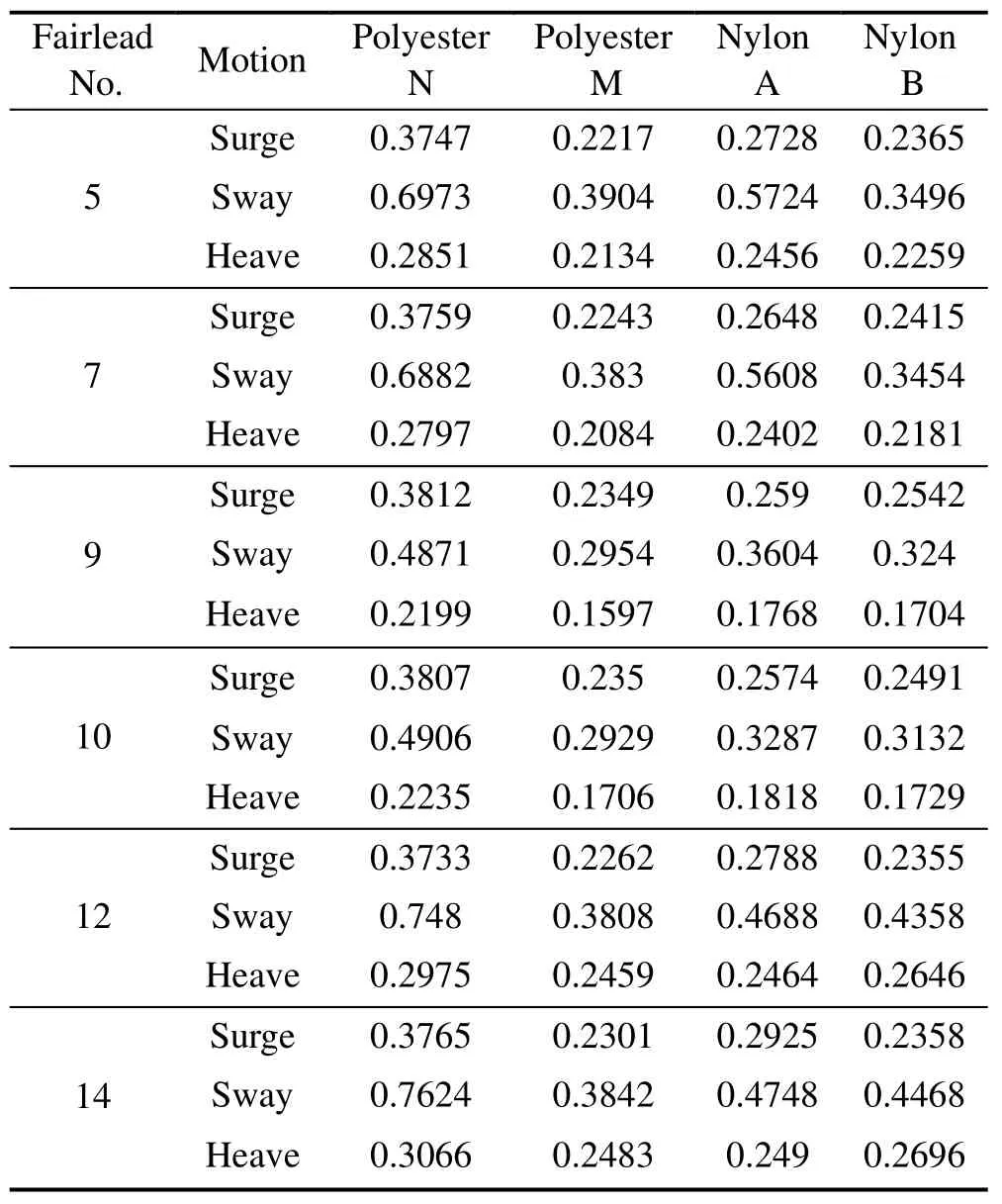
Table 3 The relative motion results with different materials

Fig. 4 Relative surge motion of vessels on the #5 fairlead
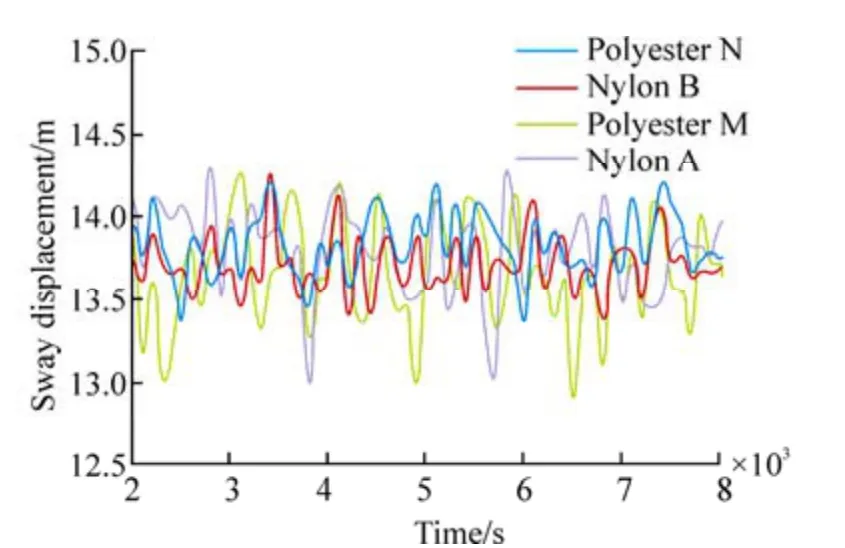
Fig. 5 Relative sway motion of vessels on the #5 fairlead
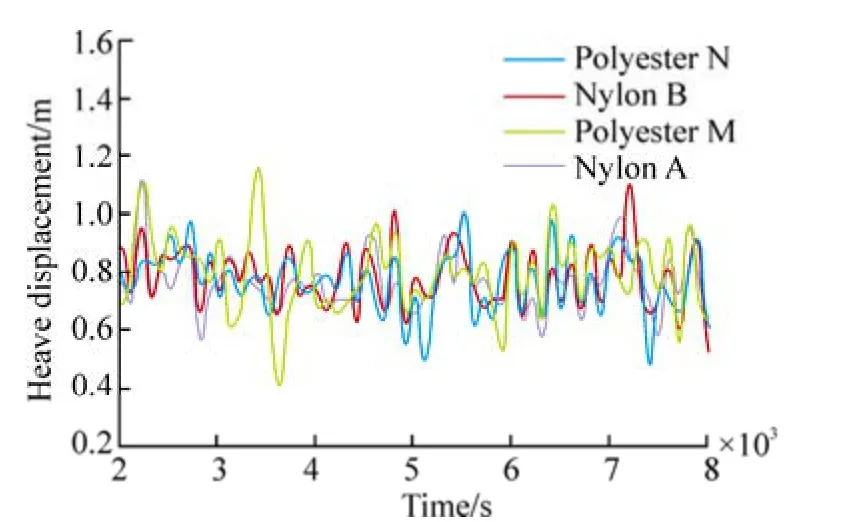
Fig. 6 Relative heave motion of vessels on the #5 fairlead
4.2 The hawser line tension
The tension with the polyester M, polyester N, nylon A and nylon B material can be acquired through time-domain simulation. The specific values are shown in Table 4. The stiffness characteristic of the hawsers has a larger effect on its own tension than on the relative motion of the FPSO and shuttle tanker. The max-tension of the hawsers using nylon B is the smallest among the four different types of fiber ropes. Take #5 fairlead as an example, the max-tension using nylon B is 191.3 kN, which is less than the numbers of the polyester M, polyester N and nylon A material by 250%,27.9% and 420%, respectively. The results indicate that the line tension can be reduced by the smaller stiffness and bigger curvature of the load-extension relationship for the fiber rope.
As for the mean tension of the hawsers, it is common for the polyester N and nylon B material to get smaller tension values than the polyester M and nylon A. The discrepancy between the mean tension of polyester N and nylon B is less than 16.4%. In terms of the hawser lines’ tension, it can be found that there exists a critical value of the load. The curvature has a smaller effect on the mean tension of the hawsers when the external load is lower than 11% MBS.The mean tension of the hawsers will be reduced with the increasing curvature when the external load exceeds 11%MBS.
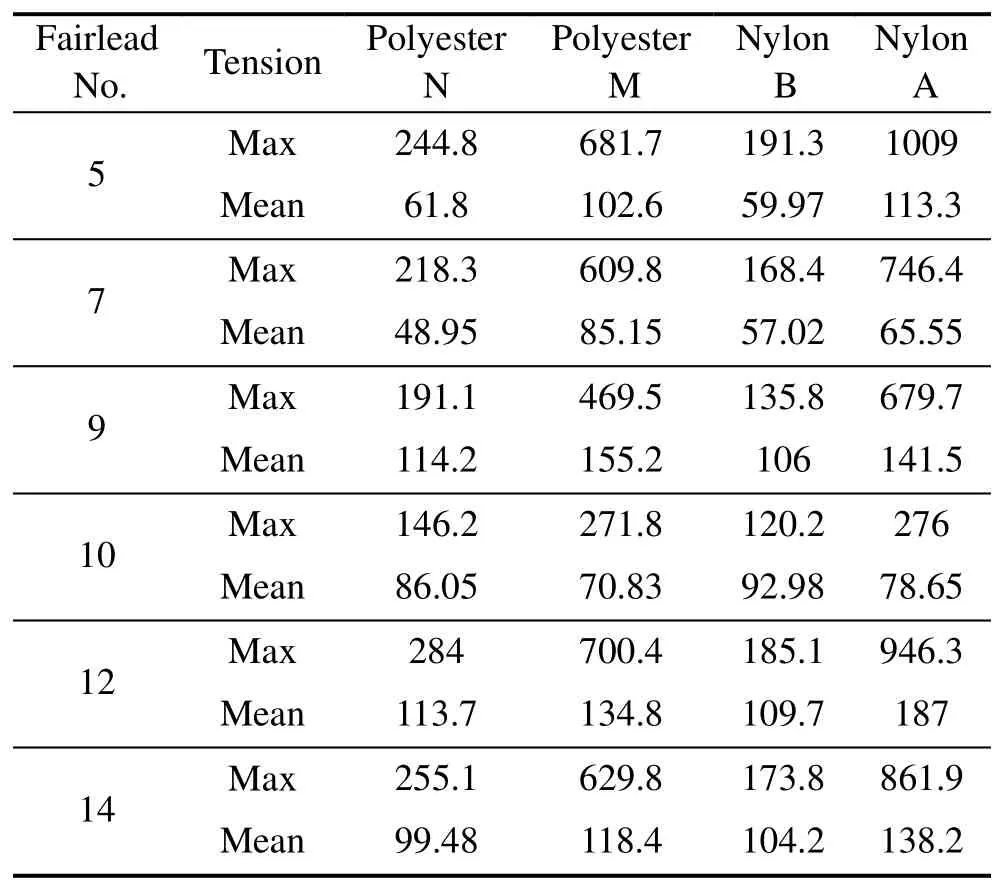
Fairlead No.Tension Polyester N Polyester M Nylon B Nylon A 5Max 244.8681.7191.31009 Mean 61.8102.659.97113.3 7 Max 218.3609.8168.4 746.4 Mean 48.9585.1557.02 65.55 9Max 191.1469.5135.8679.7 Mean 114.2155.2106141.5 10Max 146.2271.8120.2276 Mean 86.05 70.83 92.98 78.65?12 Max 284 700.4 185.1 946.3 Mean 113.7 134.8 109.7 187 14 Max 255.1 629.8 173.8 861.9 Mean 99.48 118.4 104.2 138.2
4.3 The reliability of the method
In this subsection, the strain versus the MBS curves of the three ways is shown in Fig. 7, which is based on the research conducted by the American Bureau of Shipping(2011) and Royal Lankhorst Euronete (2011). Three curves represent the upper bound linear stiffness, lower bound linear stiffness and nonlinear stiffness, respectively.
Taking the #5 fairlead as an example, the max-tension of the hawser is 913 kN, 281 kN and 677 kN when using the upper bound, lower bound linear stiffness and nonlinear stiffness, respectively. The max-tension is 681.7 kN when using the polynomial fitting function to simulate the line stiffness, which agrees well with 677 kN when using Lankhorst nonlinear stiffness. Then it can be validated that the method of fitting the nonlinear stiffness of the fiber ropes is reasonable and reliable.
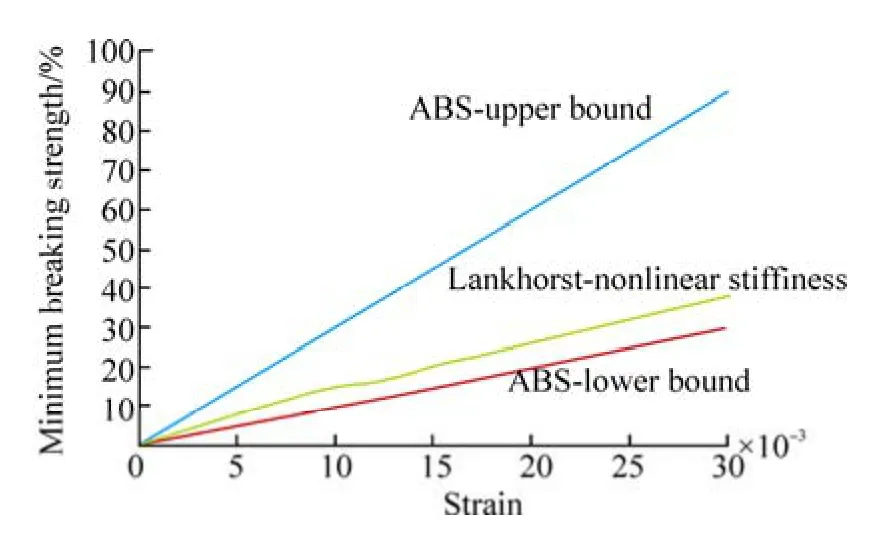
Fig. 7 Strain-MBS relationship of polyester rope
5 Conclusions
The method of polynomial fitting has proven to be an effective way to simulate the hawser lines’ nonlinear stiffness of the FPSO offloading system. Focusing on the effects of the yoke mooring system, hawser lines, fenders and the hydrodynamic interaction between the two vessels,we acquired the dynamic responses of the vessels and the hawser lines’ tension while using different types of hawser materials, which was based on the time-domain coupled calculation. The following conclusions can be drawn:
1) The polynomial fitting method for calculating the nonlinear stiffness of fiber ropes has been proven to be more accurate than linear stiffness. Therefore the nonlinear stiffness model of the fiber rope should be used in the practical engineering calculation.
2) The larger stiffness and curvature of the load-extension curve are beneficial to reduce the relative motion of the two vessels. Nonlinear stiffness has a small effect on the dynamic response of the FPSO and shuttle tanker.
3) There exists a critical value of the external load, which results in the material of one rope having multiple tension characteristics. For the polyester and nylon rope, the critical value is 11% MBS. When the external load is below 11%MBS, the max-tension of the hawser lines can be improved by lowering the curvature of the load-extension relationship or decreasing line stiffness; when the external load is above 11% MBS, the mean tension of the hawser is reduced with the increasing curvature of the load-extension relationship.
4) Comparing the dynamic response of the FPSO offloading system with the hawser lines’ tension, the nylon B is recommended to be the material for the hawser lines of the FPSO offloading system.
American Bureau of Shipping (2011).Guidance notes on the application of fiber ropes for offshore mooring. ABS Plaza,Houston, USA, 9-13.
American Petroleum Institute (2001).Recommended practice for design, manufacture, installation, and maintenance of synthetic fiber ropes for offshore mooring. API, Washington, D.C., USA,11-13.
Bosman RLM, Hooker J (1999). The elastic modulus characteristics of polyester mooring ropes.Annual Offshore Technology Conference, Houston, USA, OTC-10779.
Bridon (2007).Specialist fiber rope solutions. 3A the Centre, High Street Polegate, East Sussex, BN26 6AQ, United Kingdom,10-13.
Buchner B, Van DA, De Wilde J (2001). Numerical multiple-body simulation of side-by-side mooring to an FPSO.International Offshore and Polar Engineering Conference, Stavanger,Norway, 343-353.
Davies P, Baron P, Salomon K, Bideaud C, Labbé JP, Stéphane T,Francois M, Francois G, Bunsell T, Moysan AG (2008).Influence of fiber stiffness on deepwater mooring line response.
International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, Berlin, Germany, 179-187.
Del Vecchio CJM, Chaplin CR (1992). Appraisal of lightweight moorings for deep water.The 24th Annual Offshore Technology Conference, Houston, USA, 189-199.
Fernandes AC, Del Vecchio CJM, Castro GAV (1998). Mechanical properties of polyester mooring ropes.International Journal of Offshore and Polar Engineering, 9(3), 248-254.
Kim JW, Kyoung JH, Sablok A, Lambrakos K (2011). A nonlinear viscoelastic model for polyester mooring line analysis.
International Conference on Offshore Mechanics and Arctic Engineering, Rotterdam, Netherlands, 797-803.
Kim MH, Ding Y, Zhang J (2003). Dynamic simulation of polyester mooring lines.International Symposium on Deepwater Mooring Systems Concepts, Design Analysis, and Materials, Houston, USA, 101-114.
Liu Yingzhong, Miao Guoping, Li Yile (1997). A time domain computation method for dynamic behavior of mooring system.
Journal of Shanghai Jiao Tong University, 31(11), 7-12. (in Chinese)
Mc Kenna HA, Wong RK (1979). Synthetic fiber rope, properties and calculations relating to mooring systems.International Conference on Offshore Mechanics and Arctic Engineering,New York, USA, 189-198.
Newman JN (2004). Progress in wave load computations on offshore structures. Invited lecture on theOcean, Offshore and Arctic Engineering Conference, Vancouver, Canada.
Qian Jiayu, Sun Liping, Song Linfeng (2013). The effect of material nonlinearity on the dynamics of hull/mooring coupled system.International Conference on Offshore Mechanics and Arctic Engineering, Nantes, France, OMAE-10034.
Oil Companies International Marine Forum (1994).Prediction of Wind and Current Loads on VLCCs. Oil Companies International Marine Forum, Bermuda, London, 15-19.
Royal Lankhorst Euronete (2011).Ropes for deep water mooring.The Royal Lankhorst Euronete Group, Póvoa de Varzim,Portugal, 6-9.
Song Linfeng, Sun Liping, Wang Dejun (2013). Coupling analysis of stinger-lay barge-pipeline of S-lay installation in deep water.
Journal of Harbin Engineering University, 34(4), 415-420. (in Chinese)
Sun Liping, He Qiang, Ai Shangmao (2011). Safety assessment for a side-by-side offloading mooring system.Journal of Marine Science and Application, 10(3), 315-320.
Tahar A, Kim MH (2008). Coupled dynamic analysis of floating structures with polyester mooring lines.Journal of Ocean Engineering, 35(17-18), 1676-1685.
Tahar A, Sidarta D, Ran A (2012). Dual stiffness approach for polyester mooring line analysis in time domain.International Conference on Offshore Mechanics and Arctic Engineering,Rio de Janeiro, Brazil, 513-521.
Wang Hongwei, Luo Yong, Ma Gang, Hu Kaiye (2010). Research on fiber material mooring scheme of the deepwater semi-submersible drilling platform.JournalofShip Engineering, 32(3), 58-62. (in Chinese)
Webster William C, Kim JW, Jing XN (2012). Rod dynamics with large stretch.International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 345-354.
Yuan Meng, Fan Ju, Miao Guoping, Zhu Renchuan (2010).Mooring performance of nonlinear elastic mooring lines.
Journal of Shanghai Jiao Tong University, 44(6), 820-827. (in Chinese)
杂志排行
Journal of Marine Science and Application的其它文章
- The Current Situation of the Study on Twisted Tape Inserts in Pipe Exchangers
- Nickel Sulfide/Graphene/Carbon Nanotube Composites as Electrode Material for the Supercapacitor Application in the Sea Flashing Signal System
- Fast Prediction of Acoustic Radiation from a Hemi-capped Cylindrical Shell in Waveguide
- Optimization of Wigley Hull Form in order to Ensure the Objective Functions of the Seakeeping Performance
- Experimental Research on Flash Boiling Spray of Dimethyl Ether
- Developing a Computer Program for Detailed Study of Planing Hull’s Spray Based on Morabito’s Approach
