Optimization of Wigley Hull Form in order to Ensure the Objective Functions of the Seakeeping Performance

Hassan Bagheri and Hassan Ghassemi

Department of Ocean Engineering, Amirkabir University of Technology (AUT), Tehran 15875-4413, Iran

1 Introduction1

In the process of ship design, determining of ship geometry is problematical. Ship hydrodynamics performance is severely affected by ship hull form. From this point, finding an optimal ship hull in preliminary design stage is one of the most important concerns in the shipbuilding process. In recent decades, ship hull form optimization from point view of hydrodynamics characteristics based on computational fluid dynamics(CFD) is a method that employed for engineering design problem. In order to perform hydrodynamic optimization,objective functions need to be defined. The objective function depends on design variables and incident wave characteristics. The purpose of optimization is to minimize the objective function subject to govern equation and geometry constraints. CFD-based hull form optimization consist of a solver that’s used to evaluate the objective function, hull geometry modelling and hull lines variation that are linked to the design variables and optimization technique that used to minimize the objective function under given constraint.

Up to now, many interesting articles on the hull form optimization have been published. Bagheri (2013)employed optimization algorithm to the Wigley hull and B-series ship hull using to generate fitness curve and strip theory. Bales (1980) optimized a destroyer-type hull form,in head seas and at various speed, on the basis of analytical predictions. Grigoropoulos and Loukakis (1988) developed a numerical method, based on a nonlinear direct search algorithm to minimize RAO peak values in head regular waves. Comprehensive work carried out by Grigoropoulos(2004), Grigoropoulos and Chalkias (2010) at NTUA to optimize the various hull forms. Kukner and Sariöz (1995)optimized the seakeeping qualities of a high speed vessel that hull generating by the Lackenby method (Lackenby,1950). Some researchers have derived the hull forms by changing theparameters on the parent ones. Peacocket al.(1997) defined a mathematical model based on a multi-objective research algorithm for displacement mono-hulls. A new optimization procedure, based on a nonlinear problem was solved by direct search techniques proposed by Sariöz and Sariöz (2006). Özümet al. (2011)investigated the seakeeping qualities of fast ships,systematically varying both main dimensions and hull form parameters. Gammon (2011) use a multi-objective genetic algorithm (MOGA) to obtain an optimal fishing vessel hull form from resistance,stability and seakeeping performances point of view. Mahmood and Huang (2012)employed the CFD as a calculation tools and genetic algorithm as an optimization tools for optimization of resistance by change in bulbous bow form and Series-60 hull taken as parent hull form. Finally, Zakerdoostet al.(2013) examined the evolutionary algorithm for hull form optimization from resistance point of view. Anyway, in almost all cases, optimization procedures were based on the assumption that the optimum hull were founded when the vertical plane motions and vertical acceleration in regular head waves due to combined pitch, heave motions, is minimized.

In this paper, the objective function is to minimize the vertical bow motion of ship (at a point 0.15Lwlfrom FP=fore perpendicular) using a genetic algorithm technique. It is assumed that ship advanced in head regular waves with constant forward speed. The seakeeping solver linked with the genetic algorithm is based on strip theory. This work focused on Wigley hull and using polynomial function fitting of the hull offset points. Hull forms are changed by the polynomial function coefficients (hull lines curves coefficients) variation. The proposed optimization procedure is performed into two cases. For the first case, the only form of the hull is varied and main dimensions are fixed. In the second case, both hull form and main dimensions are varied simultaneously.

2 General problem formulations

At the preliminary design stage of a ship hull, the main particulars of the vessel such as length (L), breath (B),draught (T), longitudinal center of buoyancy (LCB),vertical center of buoyancy (VCB), longitudinal center of floatation (LCF) and all form coefficients (CB,CM,CW,CP)should be determined. Those parameters are ten parameters,three of them are main dimensions, three of them are sub-parameters, and four of the non-dimensional forms coefficients. In this paper, three of the main dimensions and three of the hull form coefficients are considered for the optimization.

2.1 Optimization problem formulation

The general mathematical form of a numerical constrained optimization problem has been represented here.Design variables and constraints conditions are used to characterize the problem. The role of design variables in hydrodynamic optimization problems is controlling the geometry of the hull during optimization procedure.Constraints are the values by which the design variables are restricted and may be separated in two types, equality and inequality constraints. A function being maximized or minimized by users is known as the objective function and the value of this function is a criterion to determine the efficiency of design optimization methodology. The standard formulation of an optimization problem mathematically is as follows:

OptimizeFfunction:

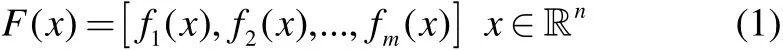
Subject to

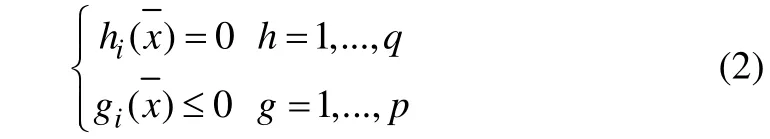
The constraints, define the feasible area. This means that if the design variables vectorbe in agreement with all constraints(equality constraint) and(inequality constraint), it belongs to the feasible area.

In this study design variables vector include the main parameters (length, breadth, draft) and the coefficients of fitted curves to hull lines, which are limited by the lower and upper bounds. The ship hull displacement also is an inequality constraint.

2.2 Hull form representation

The optimum hull form design is one of the most important problems that are viable by changing the hull form. Due to iterative hydrodynamic analysis in optimization process, generate and modify the hull form automatically have a significant effect on optimization process time.

In this work, Wigley hull is taken as parent hull form for hull form optimization. The standard Wigley hull is a mathematical displacement hull form, the geometric surface of which can be defined as:

Here,xandzare defined at the rangeand

An example of Wigley hull sections withL=3,B=0.3 andT=0.187 5 (parent hull) is presented in Fig. 1. In modeling of hull transverse sections, use a cubic polynomial function.For example; hull offset points and fitted polynomial for three sections (demonstrated in Fig. 1) of Wigley hull(parent hull) shows in Fig. 2.

Fitted polynomial function coefficient is presented in Table 1. Polynomial fitting that used has a good accuracy and low deviation. Fitting procedure to determine the polynomial coefficient is performed for each cross section of hull. Hull line changing carried out by change the specified coefficient of each cross section curve of hull. In other words, in each generation of optimization procedure,applying genetic operators lead to hull lines (initial fitted curves) coefficients varying in specified range and new hull lines generated.

Fig. 1 Body plan view of an example of Wigley hull (parent hull)

Table 1 Fitted polynomial coefficients for offset points, as shown in Fig. 2

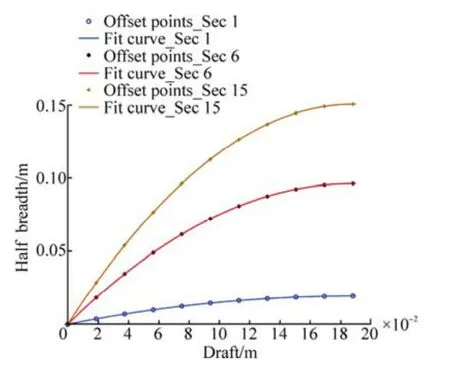
Fig. 2 Three sections offset point (as shown in Fig. 1) and fitted curved by cubic polynomial functions

2.3 Seakeeping calculations

One of the hull form optimization main goal is that minimize all of the motions. The focus of the seakeeping performance is the couple of heave and pitch motions. The seakeeping responses in head waves are most important responses for mono-hull vessels. Then all calculations were carried out for vertical motion in head waves, condition. Roll is an important ship motion, but due to difficulties in non-linearity of roll damping prediction, this motion outside the scope of present work.

The equations of motion for the advancing ship in waves may be written in the following general form:

whereMjkis the generalized mass matrix,AjkandBjkrepresent the added mass and fluid damping matrices associated with forces/moments induced in thekth mode, as a consequence of motion injth mode andCjkis the hydrostatic restoring matrix. The degrees of freedom,j, correspond to surge, sway, heave, roll, pitch and yaw asj= 1 -6 .Regarding to response of the harmonic motion of the Eq. (5),ξkis defined:

Under the assumption Eqs. (5) and (6), coupled equation of motion for heave and pitch in frequency domain can be written in following form:

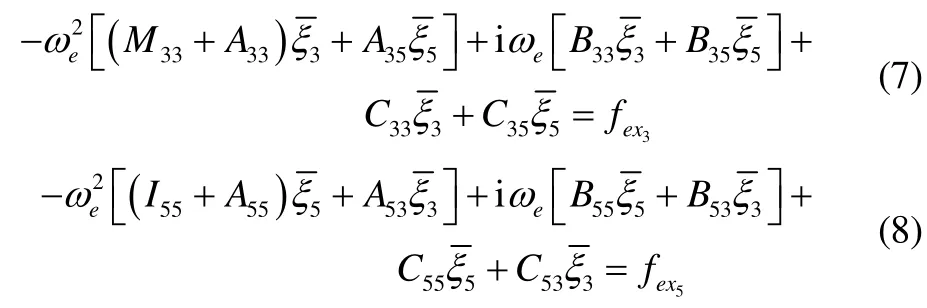
Hydrostatic restoring coefficients are calculated by Eq. (9)as follows,

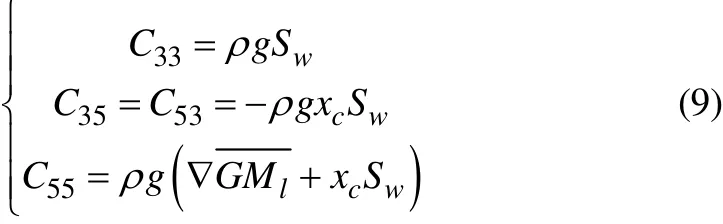
wherecxis position of center of floatationSwrepresent the water plane area andGMlis longitudinal metacentric height. In order to reduce the computing time, linear strip theory is used to solve of motion equations that adopted with described by Salvesenet al. (1970). In strip method for a slender hull form, added mass and damping coefficients are expressed as

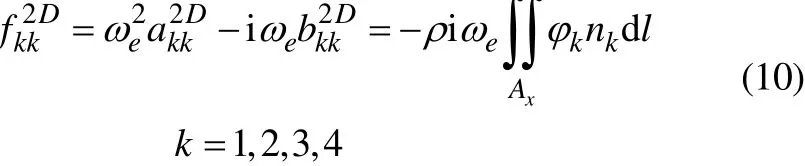
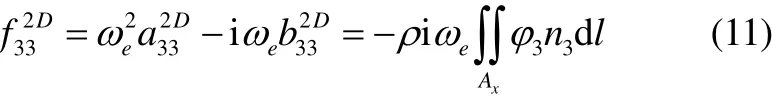
An essential part of strip method is the computation of hydrodynamic masses, damping, and exciting forces for each strip. The two-dimensional problem for each strip can be solved analytically or numerically. The analytical approaches use conformal mapping to transform semi circles to cross-sections resembling ship sections (Lewis sections).The added mass, damping and wave exciting force terms can be calculated by using well established numerical procedures. In this work, the sectional added mass and damping coefficients are calculated by using the well-known Frank Close-Fit method (Frank, 1967). For determining the coefficients, radiation problem for strips must be solved. A close-fit approach (by panel method) solves the two-dimensional problem based on source distribution method. After computing the sectional hydrodynamic coefficients and force, added mass and damping coefficients for the ship’s hull obtained by integration over the length of hull.

The calculations were performed at single speed,correspond to Froude numberFn=0.3 by considering only the vertical motion caused by the heave and pitch motions. For purpose of comparing candidate hull form, vertical motion measured at bow, from coupled the maximum heave and pitch motions.

The comparison of Delft University of Technology (DUT)report experiment (Journée, 1992) with a 3 m length Wigley hulls with length to breadth ratioL/B=10 and length to draft ratioL/T=16 in head regular wave with 4 cm wave height,heave and pitch RAO respectively are shown in Fig. 3. Using the numerical method described above for computing ship vertical motion leads to good agreement and errors between predictions and the experiments (white respect to linear theory was employed) lie within about 13% for the design Froude number (Fn=0.3). It should be noted that according to the Fig.3, the heave and pitch RAO atthat the peak value occurs, have a 70 degree phase difference approximately. The vertical bow motion (objective function) is a function of the main dimension (length, breadth and draft) and the hull offsets of the ship in the optimization process which must be minimized.

Fig. 3 Comparison of experiment and calculation for Wigley hull at Fn=0.3

2.4 Genetic algorithm (GA)

Among the class of evolutionary algorithms, genetic algorithm (GA) is the most popular algorithm for solving continuous optimization problems, i.e. for optimizing real-valued functionfdefined on a subset ofn

¡ for some dimensionngenetic algorithm is inspired by the evolution theory (Darwinian theory of biological evolution) by means of a process that is known as natural selection and the “survival of the fittest” principle. The common idea behind this technique is similar to other evolutionary algorithms: consider a population of individuals; the environmental pressure causes natural selection which leads to an increase in the fitness of the population. A set of candidate solutions can be randomly generated and the objective function can be used as a measure of how individuals have performed in the problem domain (an abstract fitness measure) the lower the better. According to this fitness, some of the better solutions are selected to seed the next generation by applying recombination and/or mutation operators to them. The recombination (also called crossover) operator is used to generate new candidate solutions (offspring) from existing ones, they take two or more selected candidates (parents) from the population pool and exchange some parts of them to form one or more offspring. Mutation operator is used to generate one offspring from one parent by changing some parts of the candidate solution. Applying recombination and mutation operators causes a set of new candidates (the offspring) competing based on their fitness with the old candidates (the parents) for a place in the next generation.

This procedure can be iterated until a solution with sufficient quality (fitness) is found or a previously set computational time limit is reached. In other words, the end conditions must be satisfied. The composed application of selection and variation operators (recombination and mutation)improves fitness values in consecutive population.

Genetic algorithm variables are divided into two categories:object and genetic variables. Variables in genetic algorithm could be as real-valued vectors. A form of an individual in GA is as follows:whereixis the object variable.In object variables mutation, each gene (biologic name of a vector) changed whit mutation rate (genetic variable) in range of their lower and upper bounds. The mutation methodology foris as follows:

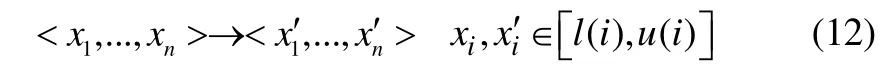
Scatter recombination is one of main type of recombination(crossover) used in GA. This type of crossover creates a random binary vector. So, the genes are selected from the first parent where the vector is a 1 and from the second one where the vector is a 0. The (m, )lsurvivor selection scheme has advantages over its competitor, the (m, )lselection scheme,but the (m, )lselection scheme is an elitist mechanism that can maintain the best solution to each generation (Eiben and Smith, 2003).

3 Optimization procedure

Hull form optimization has been applied to a Wigley hull form with principle particulars as given in Table 2, at regular head wave with heightH=4 cm.

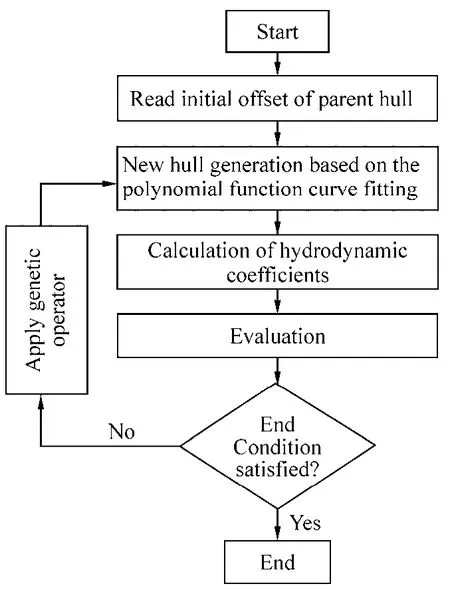
Fig. 4 Flow chart of the present calculation method

Table 2 Principles particular of Wigley hull

In the optimization algorithm, each chromosome consist of cubic polynomial function’s coefficients that fitted to hull cross section points (offset), length (water line) and draft.The design constraints that were used in this work are allowed to optimizer to change the hull offset and displacement in specified range.

The results of optimization in this study have been carried out by means of a genetic algorithm with the stochastic uniform sampling as selection operator, the scatter crossover as crossover operator and the uniform mutation as mutation operator.

Hull form optimization procedure has been applied for two cases. In the first case, only hull offset varied and the main dimensions are fixed and in another one, hull offset and main dimensions are varied simultaneously.

3.1 Wigley hull with fixed main dimensions

At this test case, also Wigley hull form (Table 2) is optimized to reach minimum vertical motion at specified bow point (means 0.15Lfrom FP).In order to perform hull form optimization, the genetic algorithm with additional parameters as follow was employed.

· Variables vector size: 58

· Crossover fraction: 0.8

· Mutation rate: 0.02

· Population size: 130

· Number of iteration: 58

In this optimization case, main hull dimensions (L,B,T)are fixed but the hull offsets are varied (Table 3). The body plan of initial hull form (solid lines) and optimized hull form(dash lines) are shown in Fig. 5. The main characteristic of parent and optimized hull forms are shown in Table 4.

Table 3 Variation percent of variables used in test cases(fixed main hull dimensions) %

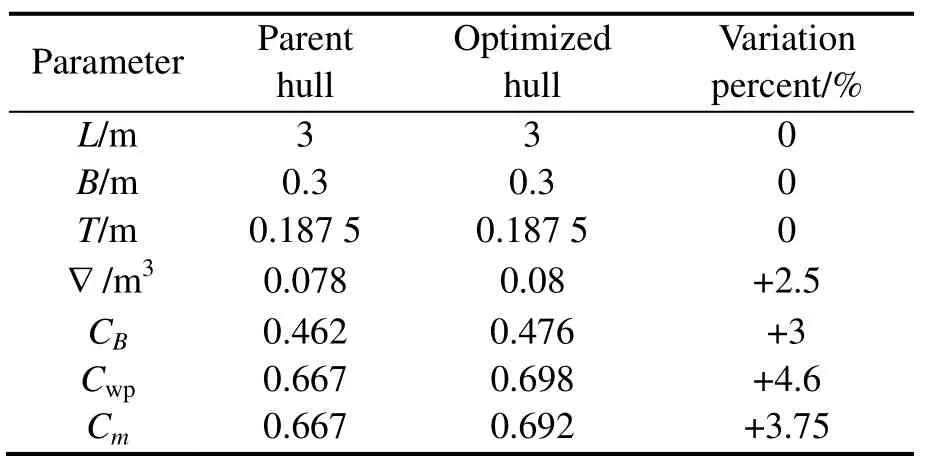
Table 4 Characteristics of the parent and the optimized hulls(fixed main hull dimensions)

Fig. 5 Body plan of original Wigley hull and optimal hull(Solid line is initial hull and dashed line is optimal hull)

During the implementation of the optimization procedure,hull offset are varied and the hull has a tendency towards larger waterplane area. Fig. 6 demonstrates the changes of the fitness value through the iterations. As can be seen in Fig.6, through the optimisation procedure vertical motion decreased. Vertical motion and acceleration of initial and optimized hulls were shown in Fig. 7. As a result of this case optimization, ship vertical motions are improved by change of the hull offset and Objective function value reduce 9%.The bow vertical motion of the parent and optimized hull at two otherFn=0.24 andFn=0.36 are presented in Fig. 8. The results show that vertical bow motion decreased for the optimized hull at both Froude number.

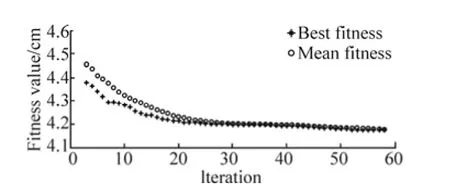
Fig. 6 History of the fitness value of the Wigley hull by iteration number

Fig. 7 Absolute vertical motion and acceleration for theinitial and optimum Wigley hull form

Fig. 8 Comparison of the vertical motion of the initial andoptimum hull forms at Fn of 0.24 and 0.36

3.2 Wigley hull with varied main dimensions

In this case, Wigley hull form that is presented in Table 2 is used to perform hull form optimization in order to obtain a hull form with minimum vertical plan motions.Optimization of hull form is carried out atFn=0.3 in regular head waves. In this case, the genetic algorithm with additional parameters as follow was used.

· Variables vector size: 60

· Crossover fraction: 0.8

· Mutation rate: 0.02

· Population size: 130

· Number of iteration: 58

In this optimization case, the main hull particulars (length,breadth and draft) and offset data are changed in specified range that is given in Table 5.

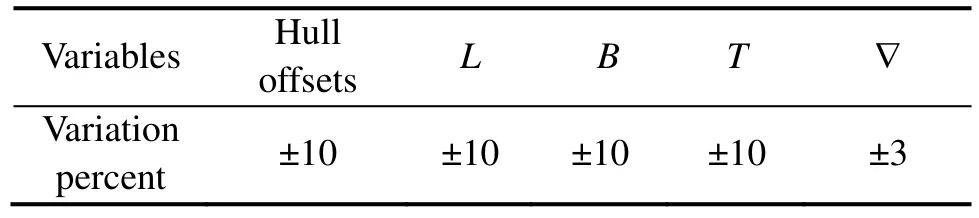
Table 5 Variation percent of variables used in test cases(not fixed main hull dimensions) %

Fig. 9 depicts body plan of the optimal hull form (dash lines), that generated as a result of using the genetic algorithm optimization technique and body plan of the initial Wigley hull (Continuous lines). The optimization procedure improved the initial hull and produced a reasonable hull form. The main characteristic of parent and optimized hull forms are given in Table 6.

Fig. 9 Body plan of original Wigley hull and optimal hull(Solid line is initial hull and dashed line is optimal hull)

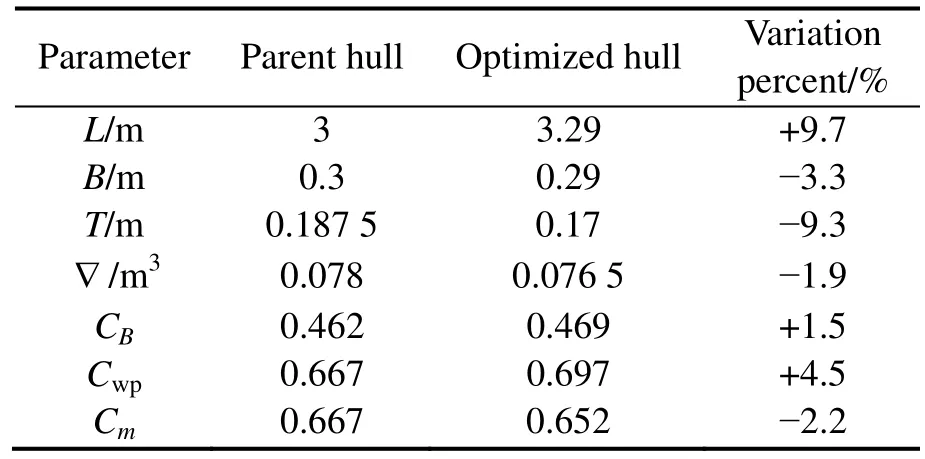
Table 6 Characteristics of the parent and the optimized hulls(not fixed main hull dimensions)

As can be seen in Fig. 9, the breadth of the optimized hull is wider than the breadth of the initial Wigley hull in fore and aft sections and thinner in the amidships. The draft of the optimized hull has decreased dramatically. The 3D view of the initial and optimized Wigley hull form is presented in Fig. 10.

Here, although all the main data and offsets are changed but it should be mentioned that length and draft are changed independently while the breadth and offsets are close each other because those are dementedly changed. This means that when breadth changes it can also cause offset changes and vice-versa. So, for variation the hull breadth fitted polynomial functions coefficients are varied in wider range.The variations of the main dimensions of the hull versus iteration number are shown in Fig. 11. Figs. 11(b) and (c)confirm that the hull has a tendency toward a lower draft and approximately fixed breadth during the optimization iterations. The length of the hull is rapidly increased in the initial iterations and after that it is remained fixed. The hull variable parameters changes are to reach minimum vertical motion’s peak value adapted to the displacement constraint.

The changes of Fitness value versus iteration number was shown in Fig. 11(d). The reduction of vertical bow motion peak’s value is 33% in this case that leads to reduction of vertical motion and acceleration in the range of wave length as shown in Fig. 12. It is interesting to note that in both test cases, trend of variation of hull form towards larger waterplane area. Here, also, the vertical bow acceleration of the optimized hull form and parent form are compared in Fig.13 at two other Froude numbers (Fn=0.24 andFn=0.36).

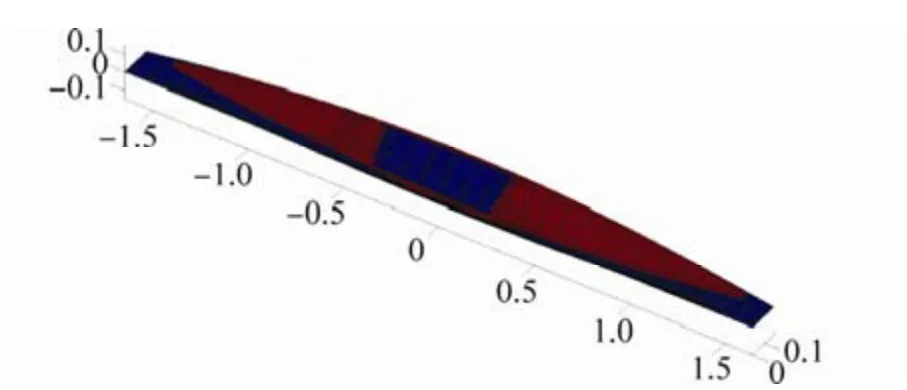
Fig. 10 Three dimensional hull form (blue is optimized hull and red is initial hull)

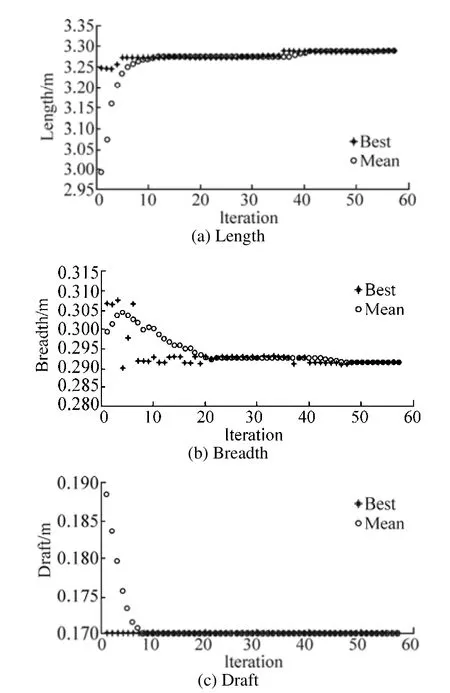
Fig. 11 Variation of dimensions parameters and the history of the fitness value of the hull by iteration number

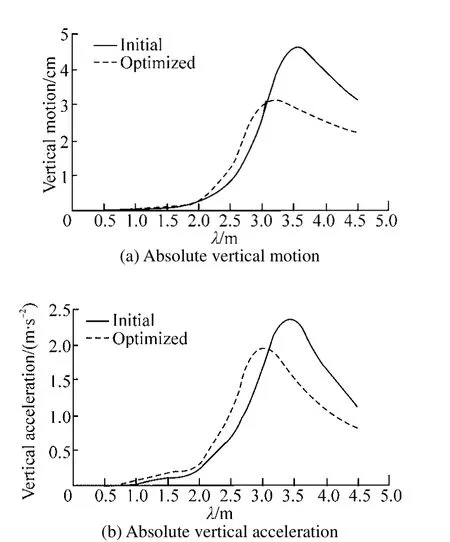
Fig. 12 Vertical motion and acceleration of the initial and optimum hull forms

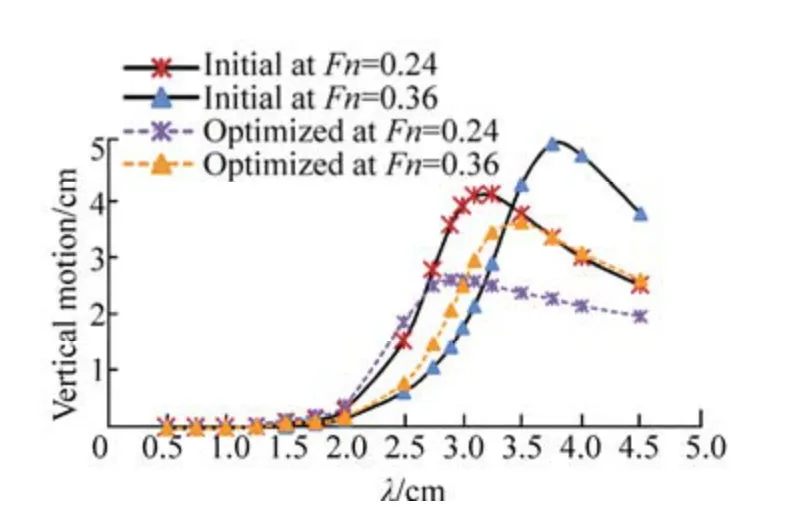
Fig. 13 Comparison of vertical motion and acceleration of the initial and optimum hull forms at Froude numbers of 0.24 and 0.36

In both test cases, applied optimization techniques lead to improve the vertical motion and acceleration. In the first test case, hull lines breadth increased and length to breadth ratio was decreased but in second case, hull line tendency toward a smaller breadth and larger length, in other word length to breadth ratio was increased. Consequently, hull form changes in both test case lead to larger waterplane area. As can be seen in Figs. 9 and 11(d), in the first test case, change of fitness value was smooth whereas in other case, fitness value has a large reduction in early phase of optimization procedure because of suddenly change in hull main particulars.

4 Conclusions

A numerical technique to optimizing the hull form in head regular waves for seakeeping performance is presented. The procedure is based on a genetic algorithm that’s linked with solver based on strip theory. The method is applied for Wigley hull and the objective function is considered the vertical motion’s peak value at bow area.

Two test cases are examined for the present optimization technique. In the first case, only hull offset varied and main dimensions are fixed and in another case, both hull offset and main dimensions are altered simultaneously. As mentioned in the first case, beam of the body line is larger while in next case, beam of body lines are narrower. It is interesting to note that in both test cases, optimization of hulls is due to larger waterplane area. It is concluded that optimized hull is dependent on the employed constraints.

This study shows that the optimization procedure with the subjected constraints can be successfully applied in order to obtain the smooth hull form with the enhanced hydrodynamic characteristics.

Acknowledgement

Authors appreciate to marine research institute (MRC) of AUT for some financial support of this project.

Bagheri H (2013).Optimization of displacement vessel hull forms from view point of seakeeping. Master thesis, Department of Ocean Engineering, Amirkabir University of Technology,Tehran, 110-120.

Bales NK (1980). Optimizing the seakeeping performance of destroyer-type hulls.Thirteenth ONR Symposium on Naval Hydrodynamics, Tokyo, 479-503.

Eiben AE, Smith JE (2003).Introduction to evolutionary computing.1st ed., Springer, Natural Computing Series, Berlin.

Frank W (1967).Oscillation of cylinders in or below the free surface of deep fluids. Naval Ship Research and Development Center, Report No. 2375.

Gammon MA (2011). Optimization of fishing vessels using a multi-objective genetic algorithm.Journal of Ocean Engineering,38(10), 1054-1064.

Grigoropoulos GJ (2004). Hull form optimization for hydrodynamic performance.Marine Technology, 41(4), 167-182.

Grigoropoulos GJ, Chalkias DS (2010). Hull-form optimization in calm and rough water.Journal of Computer-Aided Design,42(11), 977-984.

Grigoropoulos GJ, Loukakis TA (1988). A new method for developing hull forms with superior seakeeping qualities.Proceedings of CADMO 88, Southampton, 501.

Journée J (1992).Experiments and calculations on 4 Wigley hull forms in head waves. Ship Hydromechanics Laboratory, Delft University of Technology, Report 0909.

Kukner A, Sariöz K (1995). High speed hull form optimization for seakeeping.Advance Engineering Software, 22, 179-189.

Lackenby H (1950). On the systematic geometrical variation of ship forms.Trans. RINA, 92, 289-315.

Mahmood S, Huang D (2012). Computational fluid dynamics based bulbous bow optimization using a genetic algorithm.Journal of Marine Science and Application, 11(3), 286-294.

Özüm S, Şener B, Yilmaz H (2011). A parametric study on seakeeping assessment of fast ships in conceptual design stage.Ocean Engineering, 38, 1439-1447.

Peacock D, Smith WF, Pal PK (1997). Minimal ship motion hull-form design for high speed using multi-criteria optimization techniques.Proceedings of Fourth International Conference on Fast Sea Transportation (FAST’97), Sydney,Australia, 2, 653-660.

Salvesen N, Tuck EO, Faltinsen OM (1970). Ship motions and sea loads.Transactions Society of Naval Architects and Marine Engineers, 78, 250-287.

Sariöz K, Sariöz E (2006). Practical seakeeping performance measures for high speed displacement vessels.Naval Engineering Journal, 118(4), 23-36.

Zakerdoost H, Ghassemi H, Ghiasi M (2013). An evolutionary optimization technique applied to resistance reduction of the ship hull form.Journal of Marine Science and Application,12(2), 170-179.