基于改进型粒子群算法的空冷机组运行参数优化研究

李慧君，刘学敏

(华北电力大学 能源动力与机械工程学院，河北 保定071003)

0 引 言

对于直接空冷机组而言，运行参数和环境因素对其热经济性影响较大。因此，基于该因素确定最佳运行参数，对实现节能降耗具有较大意义。

目前，已有较多学者对运行参数优化进行了研究，但大都局限于对其中一个参数进行寻优计算。在排汽压力不变条件下，利用实验寻优和理论寻优法确定最佳初压，其或对实验条件要求较为苛刻，或须已知机组各级几何尺寸，可行性较差［1，2］;在机组初参数不变条件下，通过理论计算和数值模拟确定最佳排汽压力，其或未考虑环境风速的影响，或在建立几何模型和划分网格上较为复杂［3，4］。

本文以NZK600-24.2/566/566 机组为例，考虑环境风速和温度(忽略热风回流和倒灌现象)等因素影响，通过建立供电效率最大为目标函数，利用改进型粒子群优化算法［5］和本文提出的变工况计算方法，确定不同工况下最佳运行参数。

1 改进型粒子群算法原理

粒子群优化算法是于1995年提出的一种基于种群智能的随机优化算法［6，7］，经不断发展改进，已成功应用于较多实际工程问题的优化。本文应用改进型粒子群优化算法，其在收敛速度、精度及跳出局部最优能力等方面均有显著提高，为实现机组运行参数优化提供有力工具。

该算法数学描述为:在一个n 维可行解空间内(n 由具体优化问题决定)，种群粒子数为m，其中第t 次迭代时粒子i 的位置为其范围为速度为其范围为粒子个体极值为种群全局极值为该粒子第d 维的速度和位置更新公式分别为

式中:c1，c2为加速因子，取常数2;r1，r2为［0，1］范围内的随机数分别为第t 次迭代时粒子i的惯性权重因子和进化速度因子;wini为惯性权重初始值;st为第t 次迭代时种群聚集度因子;α，β 为［0，1］范围内的常数，分别取0.4，0.8;f(Pt-1i)，分别为直到t -1 次和t 次迭代为止，粒子i个体极值的适应值;ftave为第t 次迭代时所有粒子适应值的平均值;ftbest为第t 次迭代中最优解的适应值。

2 运行参数优化模型

在机组各设备正常运行条件下，设主、再热温度不变，考虑机组配汽方式和环境因素的影响，取供电效率ηcp最大为目标函数，确定最佳运行参数，即

式中:P0，Pc分别为机组初压和排汽压力，kPa;P0max，P0min，Pcmax，Pcmin分别为初压和排汽压力的上限与下限，kPa;Pe为机组功率，kW;G0为主汽流量，kg/s;ta为环境温度，℃;vF为环境风速，m/s。

为确定式(6)中目标函数值，且由于各参数间的直接数学关系难以确定，故通过对机组进行变工况计算，确定目标函数最佳值所对应的运行参数。

3 变工况计算模型

3.1 汽轮机变工况计算

(1)假定主汽流量，根据调节级参数，计算得到调节级特性曲线;利用该曲线进行调节级变工况计算［8］，确定调节汽室参数。

(2)按抽汽口划分级组，根据改进型弗留格尔公式［9］和压力级组相对内效率不变，确定各段抽汽压力与焓值，即

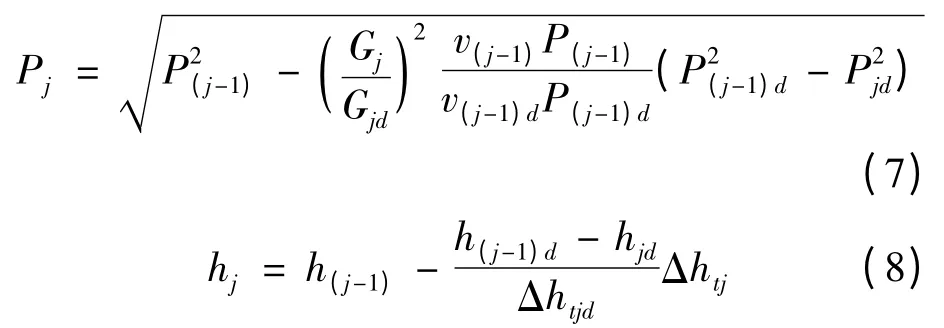
式中:Pj，vj，hj及Δhtj，Gj分别为变工况下№j 段抽汽压力(kPa)，比容(m3/kg)，焓值(kJ/kg)及第j个级组理想比焓降，kJ/kg;流量，kg/s;下角标“d”表示设计工况。

假定№j 抽汽流量Gej，可由式(7)，(8)确定№j+1 段抽汽压力与焓值;根据给水泵(或除氧器)出口压力和加热器端差，确定№j 加热器给水与疏水参数;对该加热器进行热平衡计算，通过迭代确定其抽汽流量。同理，确定其它各段抽汽参数。

(3)机组再热温度、加热器端差、排汽压力均保持不变时，其最末级组相对内效率主要受级组流量影响［10］。故排汽压力为设计值时，机组功率Ped为

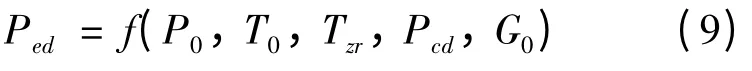
式中:T0，Tzr分别为主蒸汽温度和再热温度，℃;Pcd为设计工况排汽压力，kPa。

在相同初参数条件下，排汽压力变化时，利用机组背压特性通用方法［11］，确定实际排汽压力下机组功率Pe，即

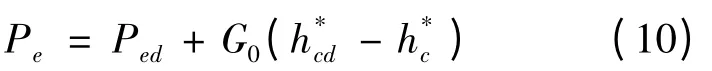
(4)以机组功率计算值与给定值之差对主汽流量进行修正，重复步骤(1)～(3)，直至功率满足精度要求。

3.2 风机系统变工况计算

其它设备厂用电不变条件下，计算供电效率须确定风机耗功，故需对风机系统进行变工况计算。

(1)已知标准环境状态下风机性能曲线及空冷系统阻力特性曲线，如图1 中曲线Ⅲ，Ⅳ所示。

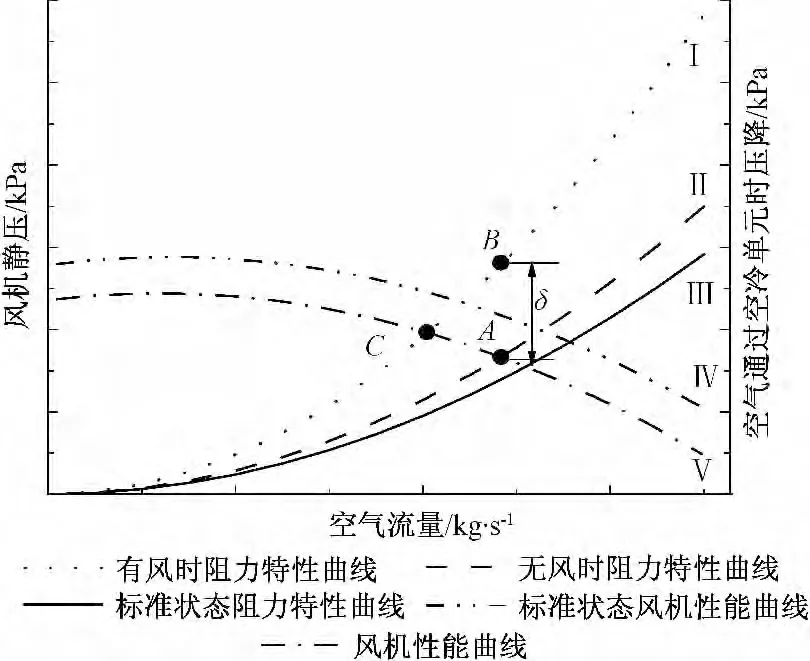
图1 风机性能曲线与系统阻力特性曲线的关系Fig.1 Correlation between fan performance and resistance characteristics

假定风机转速，由风机比例定律［12］，可得该转速和实际环境温度(无环境风)所对应的风机性能及空冷系统阻力特性曲线，如曲线Ⅱ，Ⅴ所示，其交点A 为风机工作点，两曲线方程分别为

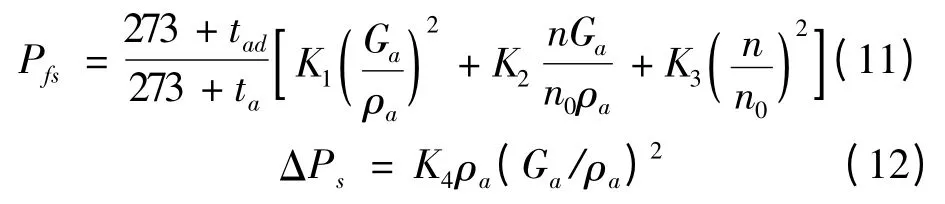
式中:K1，K2，K3及K4均为拟合系数;Pfs为风机静压，kPa;Ga为空气流量，kg/s;n0为风机额定转速，r/min;n 为风机实际转速，其范围为［0.3n0，1.1n0］［3］;tad为标准状态下环境温度，为20 ℃;ta为实际环境温度，℃;ρa为空气密度，kg/m3;ΔPs为空气通过空冷单元时的压降，kPa。

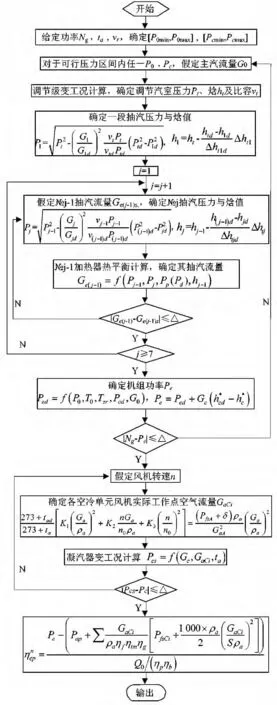
图2 变工况计算框图Fig.2 Varying condition calculation of program

(2)环境风速使风机系统阻力增加，导致其特性曲线上移［4］，由曲线Ⅱ变为Ⅰ，其与曲线Ⅴ交点C 为环境风影响下风机工作点，如图1 所示。曲线Ⅰ方程为

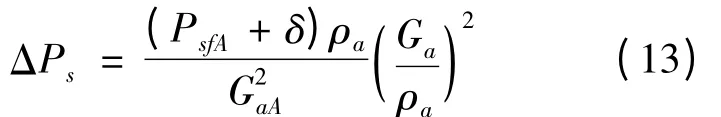
式中:PfsA，GaA分别为A 点风机静压，kPa、空气流量，kg/s;δ 为 由 环 境 风 产 生 的 损 失，δ =0.384ρavF2，kPa［13］。

从迎风面开始，环境风对风机的影响逐渐减弱，故应对各空冷单元进行计算。

(3)经对凝汽器进行变工况计算［14，15］，机组排汽压力可表示为

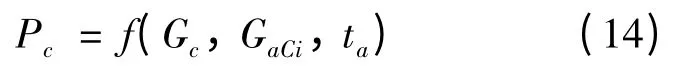
式中:GaCi为第i 个空冷单元处风机C 点空气流量，kg/s。

若风机空气流量未能满足式(14)，则用其差值对风机转速进行修正，重复步骤(1)，(2)，直至空气流量满足要求。

(4)根据各空冷单元风机实际工作点，确定总风机耗功［12］，即

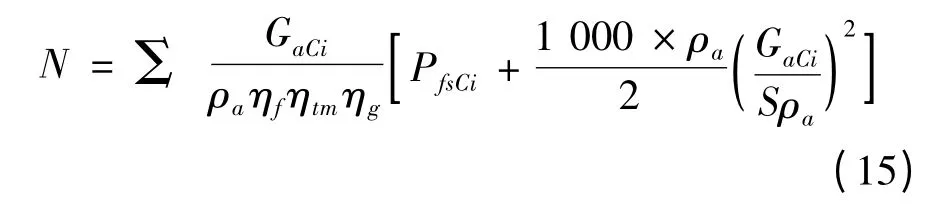
式中:PfsCi为第i 个空冷单元处风机C 点静压，kPa;ηf为风机效率;ηtm为传动效率;ηg为电机效率;S 为风机出口面积，m2。

综上所述，机组整体变工况计算框图如图2所示。其中，Pap，Q0，Pp，Pd，ηp及ηb分别为其它设备厂用电、汽轮机热耗量、给水泵出口压力、除氧器压力、管道效率及锅炉效率。

4 实例计算

以NZK600-24.2/566/566 机组为例，其配置风机直径为9.754 m，共56 台，全速时容积流量为518 m3/s，标准环境状态下其风机性能曲线和空冷系统阻力特性曲线方程分别如式(16)，(17)所示;改进型粒子群优化算法参数设置为:粒子数为10，维数为2，最大迭代次数为100。

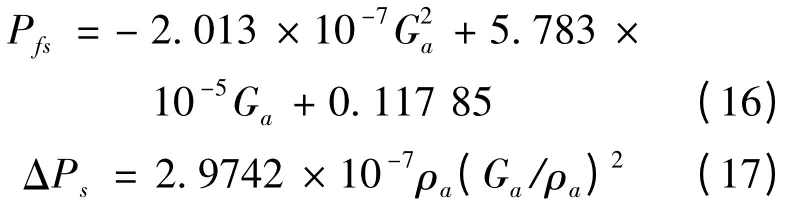
4.1 不同工况下运行参数优化计算

在不同调节阀开启状态和环境因素下，根据变工况计算模型，对75 %，50 %，40 %及30 %THA 工况进行寻优计算;其中，在较低环境温度下，当机组排汽压力低于极限压力时，需停运部分风机，重新进行寻优计算。各工况下最佳初压和排汽压力如图3 所示。

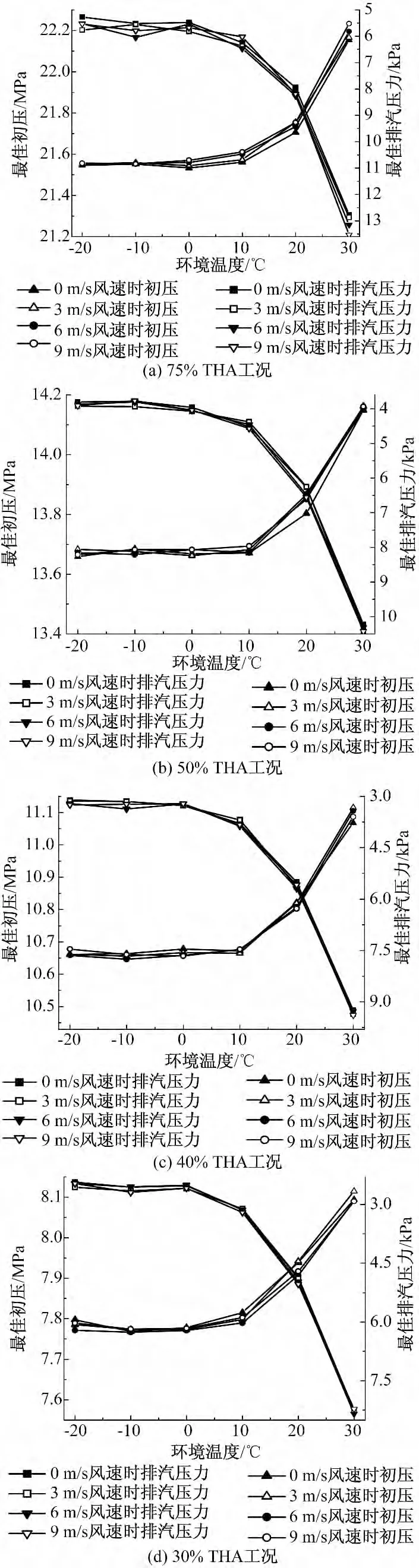
图3 不同工况和环境因素下最佳初压和排汽压力曲线Fig.3 Optimal initial steam pressure and optimal exhaust pressure curve corresponding to different loads and environmental factors

经机组运行参数优化计算，其各段抽汽等运行参数最佳值随之确定。以75 %和40 %THA 工况为例，在最佳运行参数下，电厂热耗率和供电效率如图4 所示;环境风速为3 m/s 时，其各段抽汽参数优化值如表1 所示。

图4 不同工况和环境因素下电厂热耗率和供电效率曲线Fig.4 Heat rate and power supply efficiency curve corresponding to different loads and environmental factors

表1 不同工况和环境温度下各抽汽参数优化值Tab.1 Optimal values of extraction steam conditions corresponding to different loads and ambient temperature

4.2 影响机组优化运行因素分析

机组初终参数对其经济运行影响较大，忽略主、再热蒸汽温度的变化，在给定机组负荷条件下，影响机组最佳运行的主要因素为初压和排汽压力，而影响初终压的主要因素有机组的配汽方式及环境等。

(1)随着环境因素、主调节阀开启状态及主汽流量的变化，在满足机组负荷条件下，主蒸汽初压和排汽压力随之改变，且必存在某一值，使机组热经济性最佳;

(2)随着环境温度的提高，凝汽器换热性能下降，致使排汽压力提高;为满足机组功率要求，主蒸汽初压必然增加，进而导致各段抽汽压力随之升高(如图3 和表1 所示)，电厂热耗率和供电效率均随之降低，如图4 所示。当环境温度高于20 ℃时，其对机组各运行参数影响较为突出;

(3)环境风速增大，由于风机系统阻力增加，导致排汽压力升高，机组运行参数发生变化。为保证机组经济运行，根据各参数的变化，通过目标函数重新确定最佳运行参数。因此，在同一环境温度下，当风速变化时，初压和排汽压力等参数均随之改变，但变化幅度不大，如图3所示。

5 结 论

(1)机组在不同工况下，均有最佳运行参数，使机组热经济性最佳。本文基于改进型粒子群优化模型及相关因素，建立了以供电效率最大为目标函数，以确定机组最佳运行参数;

(2)为确定目标函数值，提出了机组及风机系统变工况计算方法。该方法在不需要机组通流部分几何参数下，利用热平衡方程迭代完成各运行参数的确定;

(3)对不同工况进行了优化，确定了最佳运行参数;随着机组负荷或环境温度的变化，最佳初压、排汽压力及各段抽汽压力亦随之改变;在同一负荷和环境温度下，环境风速增加时，机组供电效率降低，且各运行参数最佳值随之改变。因此，本文所提供的模型能为机组经济运行提供一定的参考。

［1］周志平，范鑫，李明，等.超临界600MW 机组滑压运行参数优化分析与试验［J］.热力发电，2012，40 (10):50 -54.

［2］盛德仁，任浩仁，陈坚红，等.汽轮机调峰运行时蒸汽初压的优化确定［J］.动力工程学报，2000，20 (5):809 -812.

［3］郭民臣，谢静岚，李鹏，等.直接空冷机组理论最佳背压的研究［J］.动力工程学报，2012，32(7):543 -546.

［4］李海宏.600 MW 机组空冷凝汽器变工况风机优化运行研究［D］.保定:华北电力大学，2011.

［5］YANG Xueming，YUAN Jinsha，YUAN Jiangye，Huina MAO.A modified particle swarm optimizer with dynamic adaptation ［J］.Applied Mathematics and Computation，2007，189:1205 -1213.

［6］Eberhart R C，Kennedy J.A new optimizer using particle swarm theory ［A］.Proceedings of the Sixth International Symposium on Micro Machine and Human Science［C］.Piscataway，USA:IEEE Service Center，1995:39 -43.

［7］Eberhart R C，Shi Y H.Particle swarm optimization:developments，applications and resources ［A］.Proceedings of the IEEE Congress on Evolutionary Computation［C］.Piscataway，USA:IEEE Service Center，2001:81 -86.

［8］江宁，曹祖庆.调节级通用曲线的计算与应用［J］.汽轮机技术，2003，45 (1):17 -19.

［9］徐大懋，邓德兵，王世勇，等.汽轮机的特征通流面积及弗留格尔公式改进［J］.动力工程学报，2010，30 (7):473 -477.

［10］曹丽华，李勇，张仲彬.汽轮机相对内效率应达值的确定方法［J］.汽轮机技术，2002，44 (6):339 -341.

［11］徐大懋，柯严，王世勇.汽轮机功率背压特性的通用计算方法及其应用［J］.热能动力工程，2010，25 (6):605 -608.

［12］何川，郭立君.泵与风机［M］.北京:中国电力出版社，2008.

［13］戚晓冬，石红权，姜辉.横向风对空冷风机影响的实验与分析［C］.全国火电空冷机组技术交流论文集，山西:中国电力企业联合会，2005.

［14］周兰欣，杨靖，杨祥良.300MW 直接空冷机组变工况特性研究［J］.中国电机工程学报，2007，27(16):78 -82.

［15］张学镭，王金平，陈海平.环境风影响下直接空冷机组排汽压力的计算模型［J］.中国电机工程学报，2012，32 (23):40 -47.