含大型风电场系统暂态电压稳定性分析

卢锦玲，石少通，徐 超，程晓悦

(华北电力大学 电气与电子工程学院，保定071003)

0 引 言

随着风电技术的快速发展，我国风电利用逐渐走向规模化，然而大型风电场接入电网会对系统的安全稳定运行带来挑战，尤其是电压稳定问题。学者对电网静态电压稳定性进行了大量研究，提出了一些静态电压稳定分析方法和静态电压稳定指标，随着研究的深入，人们逐渐认识到了电压稳定性的动态本质，进而逐步认识到电压崩溃机理的复杂性［1］。在研究风电场接入电网后系统故障情况下电网的暂态电压稳定性时，文献［2］采用系统故障后电压幅值是否稳定在0.95 p.u.到1.05 p.u.之间去衡量，本质上是静态电压稳定指标。文献［3 ～5］采用临界故障清除时间(Critical Clearing Time，CCT)作为暂态电压稳定性指标，但是不能分析阵风情况对系统暂态电压稳定性的影响。文献［6 ～9］研究成果表明，风力发电机模型与参数的准确性在分析风力发电对电网的影响时是至关重要的，风电场装机容量、联络线路阻抗比和风电场短路容量都会影响风电系统暂态电压稳定性。因此本文在采用CCT 作为衡量系统暂态电压稳定性指标的同时，提出利用暂态电压最大跌落幅值和持续时间作为暂态电压稳定性指标，并分析了风电场不同出力水平和不同故障位置情况下系统的暂态电压稳定性。

风电发展初期风电场规模和容量都比较小，在系统发生大扰动时由于自身暂态稳定性无法保证，通常采取切机措施，系统在失去有功电源不是很大时对系统稳定性影响不大，但是对于大规模风电场接入的系统，由于风电场容量比较大，在发生大扰动时不能简单的采取切机措施，而应该通过控制提高其故障穿越能力，为系统提供暂态支持，保持系统暂态稳定。文献［8，10，11］研究了转子侧变频器控制和电网侧变频器控制，crowbar 撬棒电路保护设计用于提高双馈风电机组的故障穿越能力。上述文献研究虽然一定程度上提高了风电场的故障穿越能力，但是都忽略了双馈变速风电机组的桨距角控制对提高风电场暂态电压稳定性的作用。为了分析电网发生大扰动期间风电机组保持并网运行并对系统暂态电压稳定提供支持，文中建立了具有暂态电压支持能力的快速桨距角控制和转子侧变频器协调控制模型和crowbar保护电路，以提高电网故障期间系统的暂态电压稳定性。

1 双馈感应风电机组暂态分析模型

1.1 风速模型

为了能够精确的描述风速随机性和间歇性的特点，通常用4 种成分的风速来模拟［1］:基本风、阵风、渐变风和随机风。在暂态电压稳定分析中，由于研究的是大扰动下风电机组和电网之间的相互影响，这里仅介绍阵风数学模型，如式(1)所示。

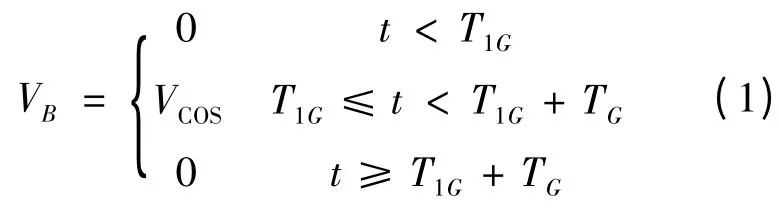
1.2 空气动力学模型

风力机通过风轮叶片捕获的风能功率为

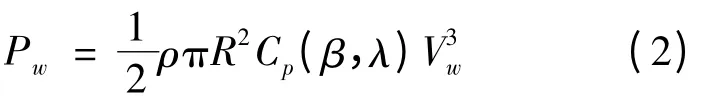
相应机械转矩为

式中:Pw为风力机输出功率;Cp(β，λ)为风能利用系数;β 为桨距角，λ 为叶尖速比;R 为风轮半径;ρ 为空气密度;Vw为风速;Mw为风力机的输出机械转矩。

1.3 轴系模型

在正常稳态运行方式下，双馈变速风电机组通过其解耦控制实现了机械部分与电气部分的解耦，轴系扭振通过变频器基本上被滤除。但是当电网出现三相短路等严重故障时，其轴系振荡就会表现出来，这只有通过对风力机与发电机质块惯量的详细模拟才能反映出来，两质量块数学模型方程［7］可表示为

式中:HT，HG为风力机和发电机惯量;TM，TE为风力机机械转矩和发电机电磁转矩;KS为轴的刚度系数;DT，DG为风力机和发电机转子的阻尼系数;θS为两质量块之间相对角位移;ωT，ωG为风力机和发电机转子转速;ω0为同步转速。

1.4 双馈感应发电机模型

同步旋转坐标系下双馈感应发电机的电压方程为［12］

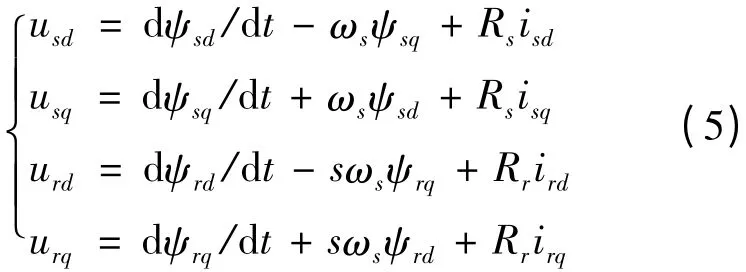
式中:ωs为坐标系旋转角速度，即为同步转速;u，i，ψ 为绕组的电压、电流及磁链;R 为绕组的电阻;下标s，r 分别代表电机的定子与转子;下标d，q 分别代表电机的d，q 绕组;s 为发电机的转差率。

2 暂态电压控制策略

大扰动下节点电压有时跌落较大，节点暂态电压稳定性较差，这时需要采取一些措施提高系统节点的暂态电压稳定性，文中建立了具有暂态电压支持能力的快速桨距角控制与转子侧变频器控制协调控制模型以及crowbar 保护电路用于提高故障期间节点的暂态电压稳定性。

2.1 桨距角控制

正常情况下桨距角控制通常用于实现最大功率追踪和风速高于额定风速时限制风力机输入的机械功率，维持发电机额定功率运行。因为故障后机端电压降低，风电机组无法按故障前发出的有功运行，会导致风电场内风电机组超速，而电压不稳定与感应电机超速密切相关［13］，因此，桨距角控制可以在暂态过程中降低风力机的机械转矩从而避免发电机转子转速增加过高而引起风机转速控制保护动作切机，为风机实现故障穿越和暂态电压恢复提供支撑。同时发现，引入桨距角控制环节，可以配合双馈风力发电机转子侧变频器的电压和无功控制策略，在电网故障期间为电压恢复提供支持。文献［14］分析得出了双馈风电机组的定子无功功率极限，如式(6)所示。

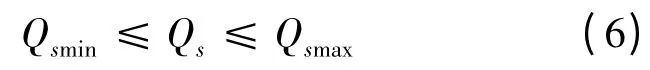
通过式(6)不难发现通过桨距角控制降低发电机定子绕组的有功输出，可以提高双馈异步发电机发出的无功功率极限，从而在电网故障过程中提供更多的动态无功支持电网电压重建，改善系统的暂态电压稳定性。常规桨距角控制通常利用测量的发电机输出有功功率与设定的有功功率参考值进行比较，将差值信号通过PI 控制器进行放大并产生桨距角的参考值用于调整风力机的桨距角从而对风电机组的机械功率和输出的有功功率进行控制。在研究系统发生大扰动后系统的暂态行为，机组的转速和转子电流等电气量响应较快，有时常规桨距角控制难以达到要求，文中对其测量量进行了改进，直接测量发电机的转子转速并通过与设定的转速参考值进行比较用于产生桨距角信号参考值，这样既能控制发电机输出的有功功率，又能对发电机故障期间转子转速进行快速控制，形成快速响应桨距角控制，控制系统原理框图如图1 所示。

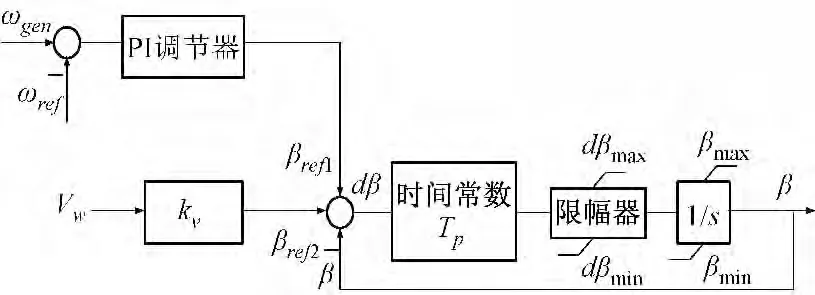
图1 改进的桨距角控制Fig.1 Modified pitch angle control

2.2 转子侧变频器解耦控制

为了充分利用变频器的控制能力并尽可能发出更多的有功，电网侧变频器一般不发出或吸收无功功率，保持与电网的无功交换为零。这意味着双馈感应电机与电网的无功功率交换只通过发电机定子完成［7］。双馈异步发电机转子侧变频器通过采用定子电压定向的矢量控制技术可以实现对定子有功和无功功率的解耦控制。通过控制转子电流的有功分量ird可以实现对定子绕组有功功率Ps的控制，转子电流无功分量irq可以控制定子绕组的无功功率Qs。ird，irq为转子d 轴、q 轴分量，它们之间不存在耦合关系，从而实现对定子Ps和Qs的解耦控制。

一般转子侧变频器无功控制的Qref值是根据稳态运行情况下发电机与电网之间无功交换要求设定为0 或一定值，这样，在电网发生故障等大扰动情况下需要风电机组提供动态无功支持时常规的变频器控制方式并不能发挥暂态电压支持作用。因此，本文对其进行了改进，通过测量电网故障电压跌落过程中的电压值与设定的正常电压值进行比较再经过一个PI 控制器得出实时动态无功参考值Qref用于转子侧变频器无功控制，能够在系统故障期间根据电压下降水平不同动态发出无功功率为系统电压恢复提供暂态支持，同时利用故障测量电压和设定的电压差值可以作为限制发电机发出有功功率的信号，通过与桨距角协调控制，在故障期间降低发电机发出的有功功率从而为发出更多无功功率提供空间。改进的转子侧变频器无功控制简化如图2 所示。

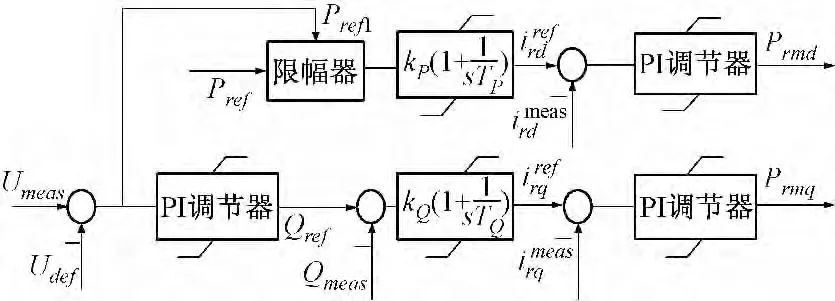
图2 改进的转子侧变频器无功控制Fig.2 Modified rotor side converter reactive power control

2.3 crowbar 保护电路控制设计

当要求风电机组具有故障穿越能力时，故障过程中及故障后一定标准下不允许风电机组切除，此时，为了保护转子侧不被故障时产生的转子过电流烧坏需要在转子侧配置crowbar 保护电路。保护电路投入后变流器失去作用，双馈风力发电机相当于普通异步风电机运行，会吸收大量无功，这对系统暂态电压恢复是不利的，变流器需要在投入一定时间后断开。关于变流器控制的恢复时间，文献［11］在研究crowbar 保护提高风电机组的故障穿越能力时得出crowbar 保护动作后退出时间应综合考虑机组电气应力约束和系统无功支持需求，一般应在crowbar 保护投入后故障清除后的1 ～2 个周波断开，恢复变流器的控制作用。

3 仿真分析

仿真系统选为新英格兰IEEE39 节点标准测试系统。节点30 为风电场接入点，节点31 为系统平衡节点。系统中其它同步发电机组暂态模型均采用计及E″d，E″q，E′d和E′q变化的6 阶模型，并考虑其励磁系统及原动机调速系统。本文采用的风电机组为额定功率为2 MW 的双馈感应发电机，定子出口额定电压为690 V。文中采用的暂态电压稳定指标有两种，一种为临界故障清除时间CCT，另一种为暂态电压的最大跌落幅值(ΔUc)和持续时间(ΔTc)来表示，如果ΔUc和ΔTc超过规定的值就可以认为暂态电压不稳定。ΔUc和ΔTc的规定值根据系统节点是否为风电场接入点分为两种，风电场接入点ΔUc和ΔTc的规定值根据国家电网低电压穿越标准设计，如果不能满足低电压穿越标准，则该节点暂态电压视为不稳定;非风电场接入点ΔUc和ΔTc的规定值根据国家电网规定的动态过程中中枢电压节点持续下降低于限定值(0.75 p.u.)超过1 s 即视为该节点暂态电压不稳定。

3.1 阵风对系统暂态电压稳定性的影响

风电机组出力为250 MW 时，阵风强度和持续时间不同对系统节点电压波动的影响，初始风速为10 m/s，阵风1 强度为5 m/s，起始时间为t=2 s，结束时间t =5 s;阵风2 强度为7 m/s，起始时间为t=2 s，结束时间t=5 s;阵风3 强度为7 m/s，起始时间为t=2 s，结束时间t=7 s。

结果显示，阵风1，2 并不会引起风电机组电气量太大变化，机端电压、转子电流和转速都在允许的范围内有不大的波动，系统稳定性良好;高强度持续时间较长的阵风3 在没有控制下可能会引起转子转速持续增加，引起风机转速保护动作而切机，转子电流和电压波动都较前两种情况严重，但并没有引起电压崩溃，在快速桨距角控制系统作用下转子转速能得到有效遏制。阵风1 情况引起的系统节点电压波动变化较大的前5 个节点如表1 所示，由表1 可见风电接入点及其附近节点和重负荷节点电压波动受阵风影响较大，暂态电压稳定性较差。

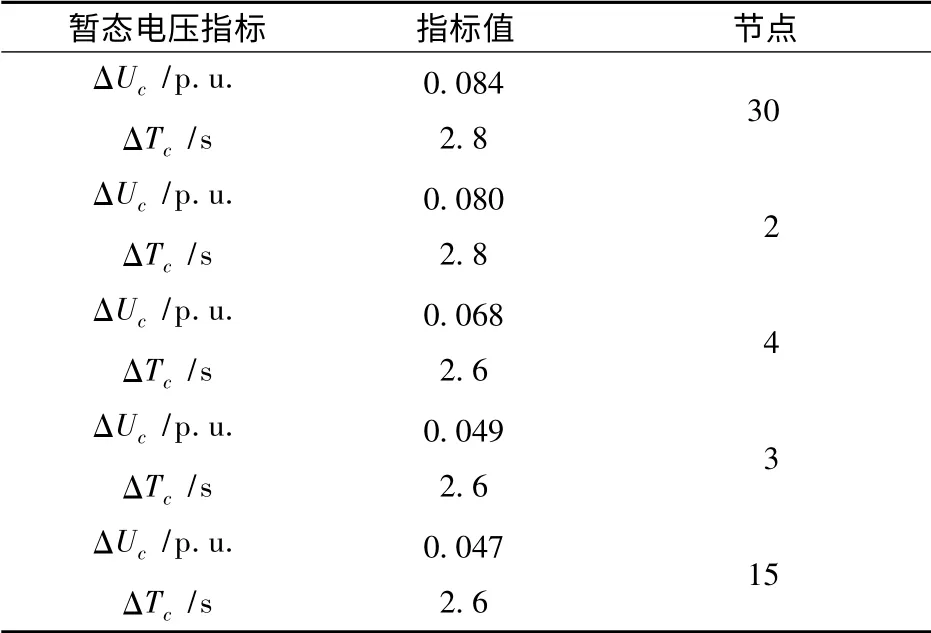
表1 风电机组出力为250 MW 时阵风1 对系统节点电压波动影响较大的前5 个节点Tab.1 The prior 5 nodes of large voltage disturbance under gust 1 with 250 MW wind power

3.2 三相短路故障下系统暂态电压稳定性及控制策略对其影响分析

为了分析在风电机组不同出力水平和系统不同地点发生三相短路故障情况下风电场接入地区节点的暂态电压稳定情况，仿真计算设定了3 个故障情景:故障1 为远离风电场接入点B7 处发生三相短路故障;故障2 为距离风电场较近的系统重负荷节点B4 处发生三相短路;故障3 为风电场接入点变压器高压侧B2 处发生三相短路。分别研究不同故障情景下风电机组出力水平为100 MW，180 MW 和250 MW 时利用上述两个暂态电压稳定指标去分析风电场接入点及其附近节点暂态电压稳定性情况，并分析文中提出的改进方法是否能够提高风电机组的暂态电压稳定性，由于暂态过程比较短，故障过程中假设风速保持不变。

3.2.1 CCT 分析结果

不同故障情景下风电机组出力水平为100 MW，180 MW 和250 MW 时，改进控制系统前CCT1 和改进后CCT2 如表2 所示。

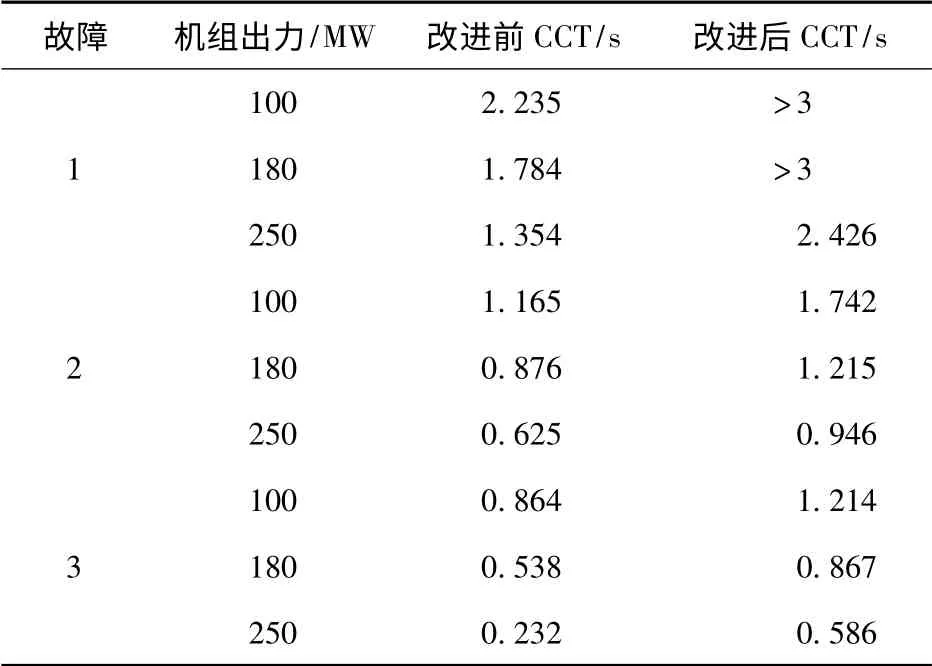
表2 风电机组不同出力水平下系统临界故障清除时间Tab.2 CCT in different wind power outputs and fault position

由表2 可见风电机组高出力水平下系统发生故障及故障离风电场接入点越近系统的临界故障清除时间越短，系统的暂态电压稳定性越弱。对比控制系统改进前后的CCT 可以发现，改进后的控制模型能够有效提高系统故障时的CCT，提高了系统的暂态电压稳定性。

3.2.2 暂态电压最大跌落幅度分析

以风电场出力为250 MW 时不同故障情景下原来控制系统和改进控制系统后的仿真结果进行对比分析。

(1)故障1 情况原先控制系统下和改进控制系统后风电机组机端电压、转子电流、发出有功功率和发出的无功功率如图3 ～图6 所示。

结果表明，此种故障情景对风电机组的影响

图3 机端电压Fig.3 Voltage of the generator

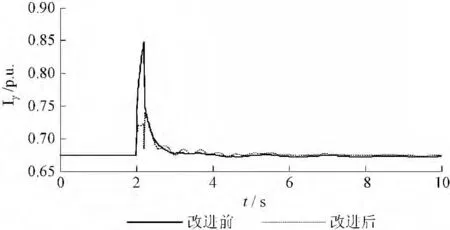
图4 转子电流Fig.4 Roto current

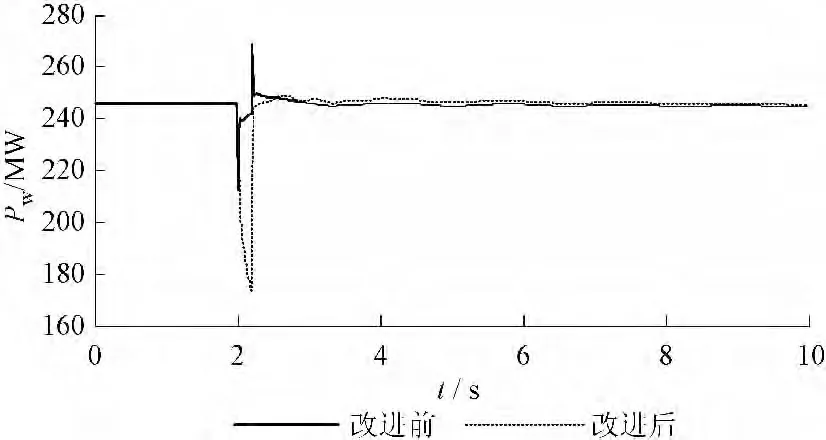
图5 风电场发出有功功率Fig.5 Active power of the wind farm

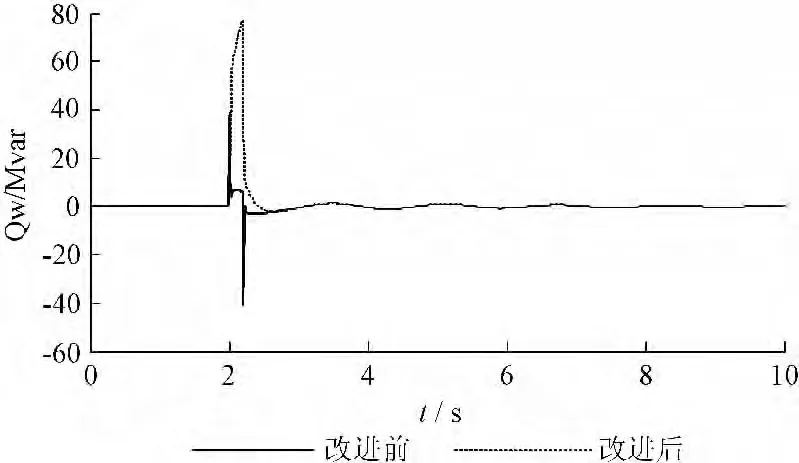
图6 风电场发出无功功率Fig.6 Reactive power of the wind farm

并不十分严重，在原先控制系统下风电机组转子电流在故障发生后有所增加，但是在允许的范围内，故障期间风电机组发出的有功功率几乎不变，发出的无功功率基本为0，机端电压最大跌落到0.7461 p.u.;而改进控制系统作用下，通过测量风电机组故障电压与设定电压的差值能够动态控制发电机发出的无功为系统电压恢复提供支持，并能在故障期间适当降低发出的有功功率为发出更多无功功率提供空间，在改进控制系统下，风电机组转子电流故障期间增幅较小并且机端电压最大跌落幅度有所减少，电压最大跌落到0.8527 p.u.，较改善前提高了11 %左右。

(2)故障2 情况原先控制系统下和改进控制系统后风电机组机端电压、转子电流、发出有功功率和发出的无功功率如图7 ～图10 所示。

结果显示，该情景下控制系统改进前后与故障1 相比转子电流和风电机组发出有功和无功相类似，改进控制系统能够使风电机组在故障期间检测到机端电压下降后能够降低有功功率并且发出无功功率，降低了转子电流的增幅，并为电压恢复提供了支持，此种情景下，由机端电压图7可以发现，此种情景下，改进的控制系统作用更加明显，原先控制系统下在故障期间机端电压下降幅度较大，跌落到0.559 2 p.u.，而改进控制系统下机端电压只跌落到0.742 4 p.u.，提高了约18 %左右。对于离风电机组接入点较近区域发生三相短路故障时，对风电机组的影响是比较明显的，转子电流会迅速增加，机端电压下降较严重，改进控制系统能够有效降低故障期间转子电流的增幅，并且明显改善故障期间电压跌落，效果比较明显。

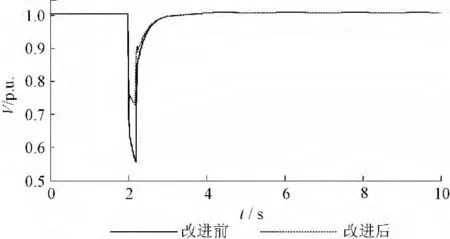
图7 机端电压Fig.7 Voltage of the generator

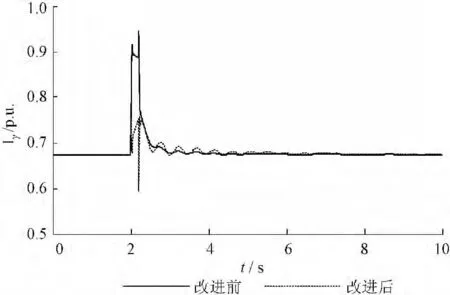
图8 转子电流Fig.8 Rotor current

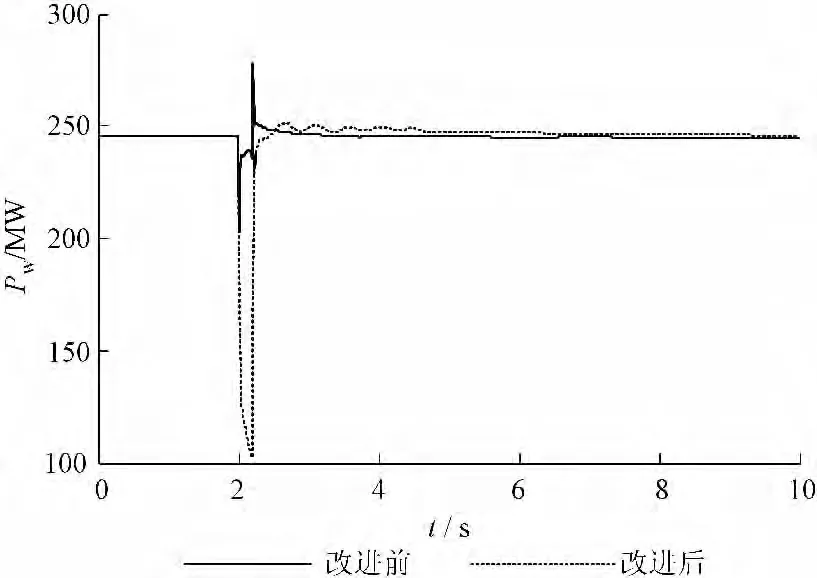
图9 风电场发出有功功率Fig.9 Active power of the wind farm

图10 风电场发出无功功率Fig.10 Reactive power of the wind farm

(3)故障3 情况原先控制系统下和改进控制系统后风电机组机端电压、转子电流、发出有功功率和发出的无功功率如图11 ～图18 所示。

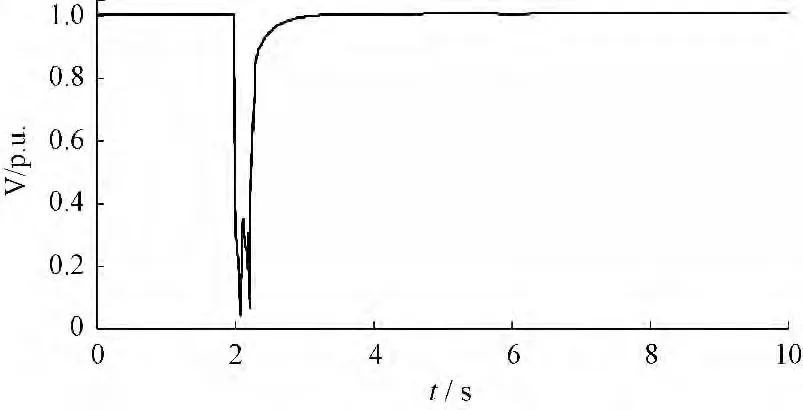
图11 改进前机端电压Fig.11 Voltage of the generator before modified

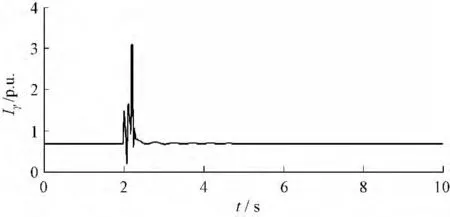
图12 改进前转子电流Fig.12 Rotor current before modified

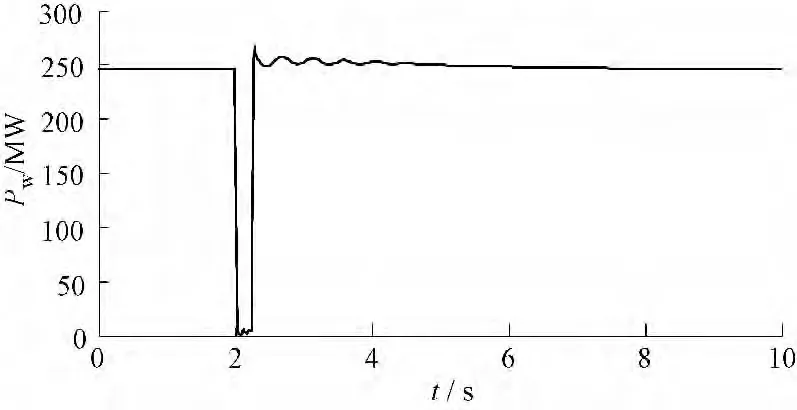
图13 改进前风电场发出有功功率Fig.13 Active power of the wind farm before modified

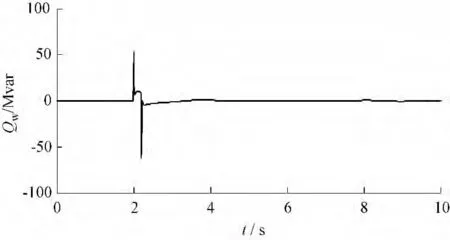
图14 改进前风电场发出无功功率Fig.14 Reactive power of the wind farm before modified

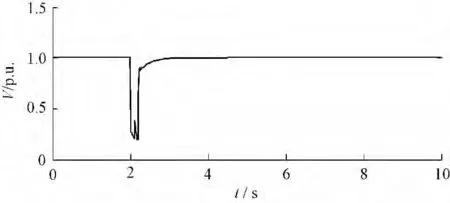
图15 改进后机端电压Fig.15 Voltage of the generator after modified

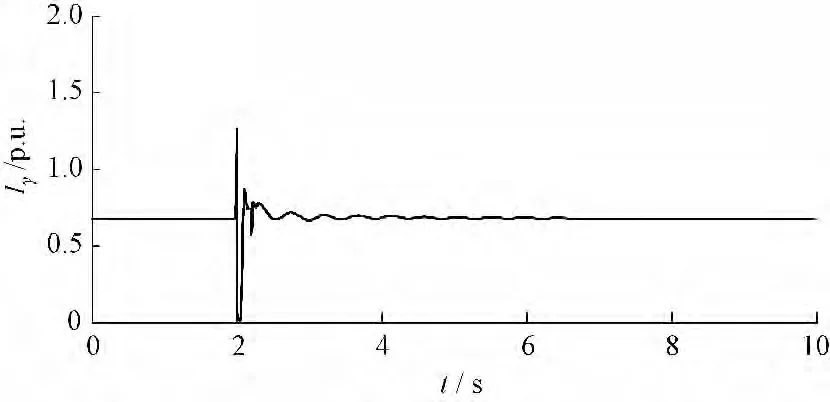
图16 改进后转子电流Fig.16 Rotor current after modified

图17 改进后风电场发出有功功率Fig.17 Active power of the wind farm after modified

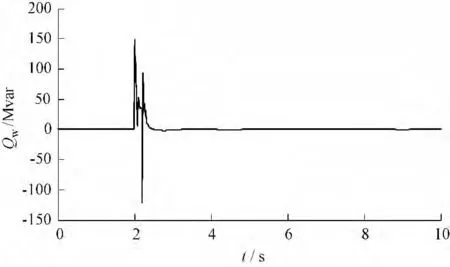
图18 改进后风电场发出无功功率Fig.18 Reactive power of the wind farm after modified

结果显示，此故障情景最严重，当风电机组接入点变压器高压侧发生三相短路故障时，原先控制系统下转子电流迅速增加并且超过了3 p.u.，这在风电机组的保护设置中是不允许的，风电机组的转子过流保护一般设定值为2 p.u.，原先控制系统下故障期间转子电流超过设定值较多会引起过流保护动作切机，故障期间电压跌落幅度也最大，电压最低跌落到0.164 p.u.，一般情况下如果风电机组的故障穿越电压设定的不够低也会引起风电机组低压保护动作切机，风电接入点暂态电压失去稳定。改进控制系统下，故障期间撬棒保护电路会动作，并且能够控制风电机组故障期间发出无功功率，有效降低了转子电流的增加，将故障时转子电流控制到1.5 p.u.左右，避开了过流保护动作，使故障期间风电机组不至于因转子电流过高而切机，但是改进控制系统对提高此种故障情景下机端电压的降落效果较差，只从0.122 p.u.提高到了0.171 p.u.，约5 %。此故障情景仿真表明，改进控制系统能够对风电机组机端三相短路严重故障时转子电流增加进行有效遏制，但是对改善机端电压效果不是很明显。对于如何提高风电机组接入线路变压器高压侧发生三相短路故障情景下机端电压水平，文献［1，15］ 等提出利用动态无功补偿装置SVC 和STATCOM 能够有效提高故障期间风电机组的电压水平，为风电接入区域电压快速恢复提供支持。

4 结 论

基于变速双馈风电机组，建立了详细的风电机组暂态数学模型，对大型风电场接入系统后可能引起系统电压失稳的机理进行了探讨，对比分析了不同风电接入容量、不同故障位置以及不同阵风强度下系统节点的暂态电压稳定性。在DIg-SILENT/PowerFactory 软件中通过建立风电机组的综合控制模型和改进桨距角控制和转子侧变频器控制，提出了具有暂态电压支持的快速桨距角控制和转子侧变频器协调控制模型用于提高风电接入地区的暂态电压稳定性。算例仿真证明了建立的风电机组暂态数学模型和暂态电压稳定指标的有效性，结果表明所建立的具有暂态电压支持的快速桨距角控制和转子侧变频器协调控制模型一般情况下能够有效改善风电机组的暂态电压稳定性。针对风电接入点变压器高压侧发生三相短路的严重情况，改进的控制策略并不能大幅提高风电机组暂态电压跌落，需要考虑通过与SVC 和STATCOM 等动态无功补偿配合以保持此故障情况下风电机组并网运行和提高系统暂态电压稳定性。需要指出的是，本文仅采用标准算例进行了仿真分析，对于文中所提出的改进的控制策略对含大型风电场系统暂态电压稳定性的改善效果采用实际电网和风电场数据进行仿真是下一步需要进行的工作。

［1］潘文霞.大型风电场电压稳定性分析与控制研究［D］.南京:河海大学，2004.

［2］刘伟.风电接入对电网电压的影响分析［D］.保定:华北电力大学，2010.

［3］石立宝，戴世强，徐政，等.大规模双馈型风电场并网的系统暂态稳定仿真［J］.电力系统及其自动化学报，2009，21 (4):1 －6.

［4］迟永宁.大型风电场接入电网的稳定性问题研究［D］.北京:中国电力科学研究院，2006.

［5］张锋，李明霞，樊国伟，等.风电接入对地区电网暂态电压稳定性的影响［J］.中国电力，2011，44(9):17 －20.

［6］吴涛，于啸，郭嘉阳，等.暂态稳定计算中双馈型风电机组模型与参数的实证分析［J］.电网技术，2011，35 (1):100 －104.

［7］黄梅，万航羽.在动态仿真中风电场模型的简化［J］.电工技术学报，2009，24 (9):147 －152.

［8］李辉，赵斌，史旭阳，等.含不同风电机组的风电场暂态运行特性仿真研究［J］.电力系统保护与控制，2011，39 (13):1 －6.

［9］张红光，张粒子，陈树勇，等.大容量风电场接入电网的暂态稳定特性和调度对策研究［J］.中国电机工程学报，2007，27 (31):45 －50.

［10］袁晓冬，邱志鹏，李群，等.双馈型风电机组网侧换流器无功功率调节控制策略［J］.电力自动化设备，2011，31 (8):16 －19.

［11］徐殿国，王伟，陈宁，等.基于撬棒保护的双馈电机风电场低电压穿越动态特性分析［J］.中国电机工程学报，2010，30 (22):29 －35.

［12］Akhmatov V.Analysis of dynamic behavior of electric power systems with large amount of wind power ［D］.Copenhagen:Technical University of Denmark，2003.

［13］孙华东，周孝信，李若梅，等.感应电动机负荷参数对电力系统暂态电压稳定性的影响［J］，电网技术，2005，29 (23):1 －6.

［14］郎永强，张学广，徐殿国，等.双馈电机风电场无功功率分析及控制策略［J］.中国电机工程学报，2007，27 (9):77 －81.

［15］张锋，晁勤.STATCOM 改善风电场暂态电压稳定性的研究［J］.电网技术，2008，32 (9):70 －73.