利用调频率匹配的DRFM欺骗干扰检测方法

卢云龙,李 明,闫 琰

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

利用调频率匹配的DRFM欺骗干扰检测方法

卢云龙,李 明,闫 琰

(西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071)

针对转发式线性调频(LFM)有源欺骗干扰的检测问题,提出了基于干扰信号谐波分量调频率匹配的检测方法.数字射频存储器存在谐波效应特性,该方法通过分析干扰信号的频谱特征规律,建立谐波分量调频率参数库.在雷达距离门内同时存在目标回波和干扰信号的情形下,利用分数阶傅里叶变换检测雷达回波中LFM信号分量并估计其调频率,通过与参数库进行匹配分析,实现干扰信号的检测.仿真结果验证了该方法的有效性.

数字射频存储器量化;有源欺骗干扰;分数阶傅里叶变换;参数估计

有源欺骗干扰会严重降低雷达对目标的检测性能.而基于数字射频存储器(DRFM)的距离波门拖引干扰(RGPO)和速度波门拖引干扰(VGPO)与雷达发射信号具有很强的相干性,干扰信号在相干雷达中可以获得相当大的增益,使得雷达难以区分目标和干扰[1-2].

近年来针对DRFM欺骗干扰信号的研究主要有:文献[3]通过在每个脉冲重复间隔期间发射不同初始相位的信号,利用目标回波与干扰信号在多普勒频谱域的差异实现干扰检测.文献[4]通过联合干扰信号幅度波动特征、高阶累积量以及双谱特征来识别具体干扰类型.文献[5-6]研究了有源欺骗干扰在合成孔径雷达成像中的特性.文献[7-8]着重分析了宽带DRFM干扰信号的特性及硬件实现.文献[9-10]分析了基于DRFM的距离波门拖引干扰(RGPO)信号的频谱,详细推导了DRFM时延量化特性对干扰信号带来的频域细微变化特征.在此基础上,文献[11-12]分析了DRFM时延函数和相位联合量化对RGPO信号的影响,分析量化后谐波谱线的特性,并得出相对相位量化.时延函数量化对信号的影响可以忽略.文献[13]分析了距离-速度同步拖引干扰的理想频谱与实际频谱特征,这些频谱特征在理想环境下有较明显的差异,能够为雷达检测该类干扰提供依据.但是,上述文献中对干扰信号频谱特征的分析都是基于单频脉冲雷达信号,而在实际检测环境中,干扰信号谐波谱线易受噪声等因素影响而不易检测.同时文献中没有考虑雷达回波中同时存在目标回波和干扰信号的情形.

事实上,现代雷达广泛采用脉内频率调制信号,如LFM信号.对于波门拖引干扰,在波门捕获期,雷达回波由目标回波与干扰信号组成,如能在此阶段就检测出干扰信号,可使雷达更及时地采取抗干扰措施.因此,笔者在上述研究成果基础上,分析了DRFM线性调频有源欺骗干扰信号的频谱,推导出干扰信号谐波频谱的特征规律并建立谐波分量调频率参数库,并提出一种基于谐波分量调频率参数匹配的干扰检测新方法.该方法通过建立可能存在的干扰信号谐波频谱调频率参数库,利用分数阶傅里叶变换估计雷达回波中LFM信号调频率,并与参数库进行匹配检测.由于LFM信号调频率参数受噪声等因素影响小,通过参数匹配检测,该方法能够在复杂的电磁检测环境下有效检测出有源欺骗干扰信号.分析发现目标回波与干扰信号的叠加并不影响干扰信号的谐波特性规律,因此该方法在波门捕获期就可以有效检测出干扰信号.

1 信号模型

设雷达发射基带信号为

DRFM下变频后接收信号可以表示为

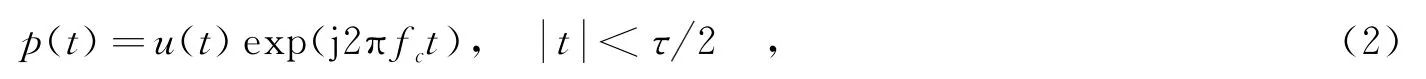
式中,fc=fI+fd,fI为干扰机下变频频率,fd是目标的多普勒频率.

对于距离波门拖引干扰而言,在分析干扰信号相位量化效应时,时延函数离散量化对其的影响是可以忽略的[9].设距离拖引时延函数可表示为理想线性函数c(t)=at,a为拖引率,则经DRFM相位量化后的线性调频欺骗干扰可表示为

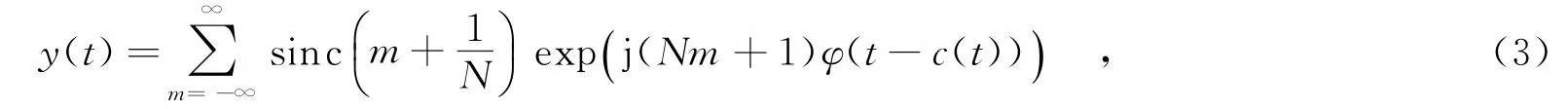
其中,N=2M,M为量化位数,φ(t)为p(t)的相位,φ(t)=2πfct+πμt2,m对应不同的谐波分量.

将c(t)=at代入式(3),并令

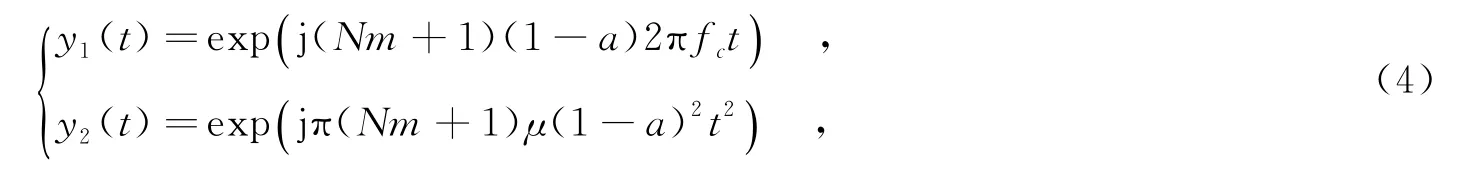
则有

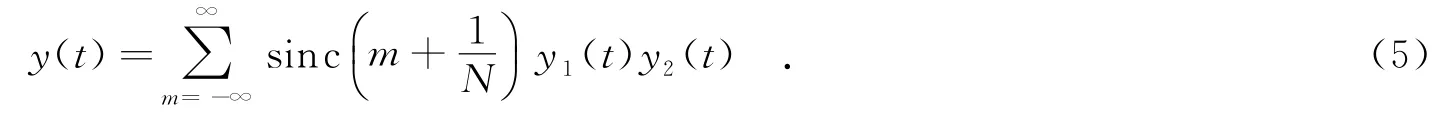
在雷达距离门内同时存在目标回波和干扰信号的情形下,回波信号经雷达接收机混频后可表示为[2]

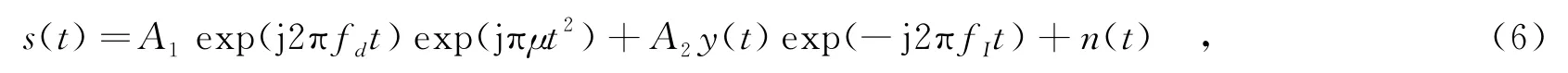
式(6)右边第1项为目标回波,第2项为干扰信号,A1、A2表示幅度,通常A1＜A2.n(t)为高斯白噪声.

2 基于谱参数匹配的干扰检测方法

由DRFM产生的转发式欺骗干扰信号可视为截获雷达信号的复制品,因其与雷达发射信号的高度相干性而难以识别.尤其在波门内同时存在目标回波和干扰信号阶段,干扰机对截获雷达信号的调制很小,传统的检测方法难以有效检测出干扰信号.由于DRFM干扰机存在谐波效应,笔者在分析线性调频干扰信号相位量化模型时发现,干扰信号的调频率由干扰机量化位数及雷达发射信号调频率决定,并且与目标回波调频率参数差异较大,因此提出一种新的干扰检测方法.首先通过建立可能存在的干扰信号谐波频谱调频率参数库,然后检测并估计雷达回波中LFM分量调频率参数,并与参数库进行匹配分析,完成干扰信号的检测.

2.1 频谱特征分析

很多文献已有证明,当Bτ≫1,μ＞0时,u(t)的频谱为

同理,当信号为负调频,即μ-=-μ时,可求得

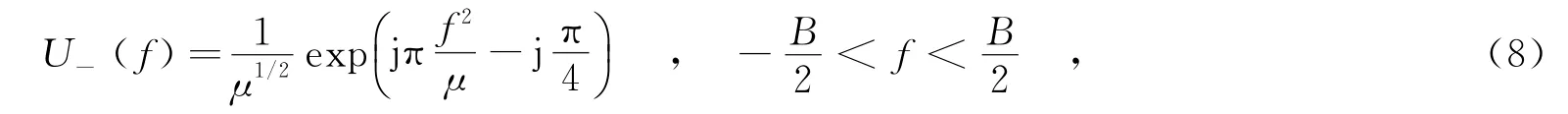
即U+(f)与U-(f)共轭相等,这并不影响u(t)频谱的带宽和形状.

根据傅里叶变换定义可得y2(t)的频谱为

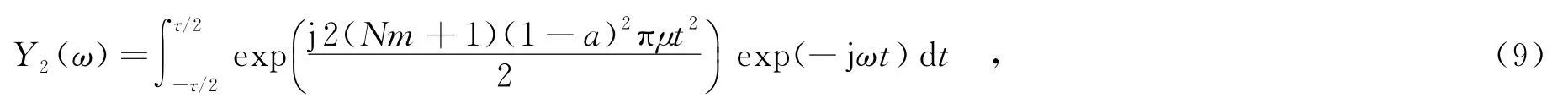
令

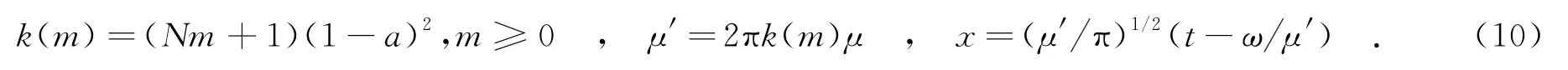
代入式(9),可得

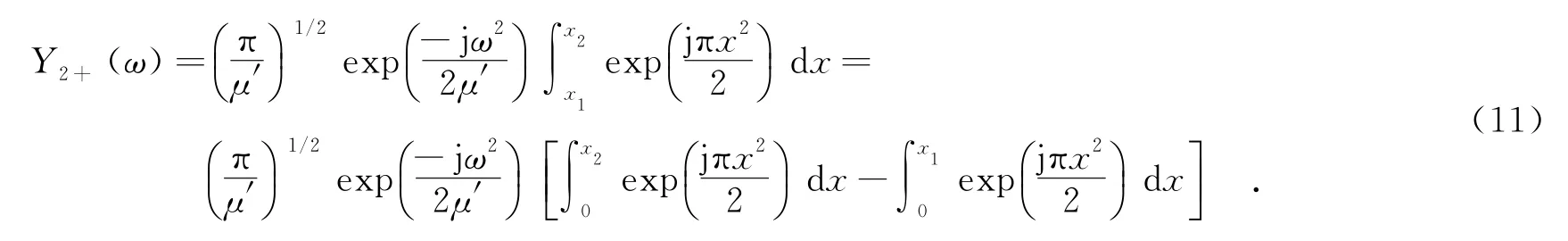
之后的推导过程与求线性调频信号u(t)的频谱U(f)类似,很多文献有详细推导过程,这里不再重复,直接给出最终结果:

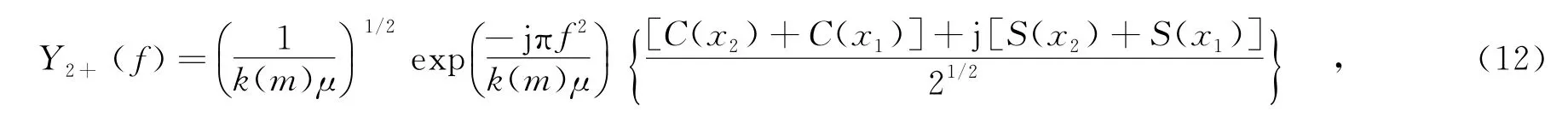
式中,C(x),S(x)为菲涅耳积分,当Bτ≫1时,式(12)可以表示为

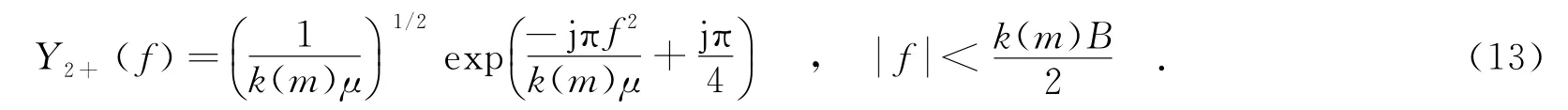
同理,当m＜0时,信号为负调频,有

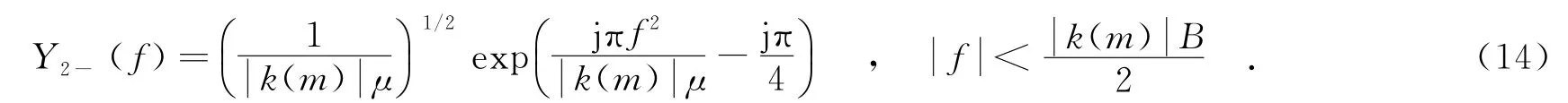
结合以上分析,由式(5)、(13)、(14),可以得到y(t)的频谱

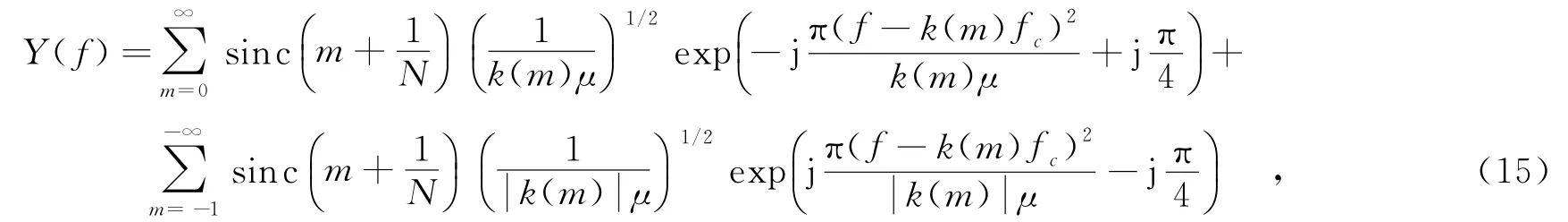
不考虑噪声对信号频谱的影响,则雷达回波经接收机混频后信号s(t)的频谱可表示为

在实际应用中,拖引率a一般为10-6数量级,认为(1-a)2≈1,则由式(16)得s(t)频谱近似为

图1 目标信号与干扰信号的频谱(时频)图

由式(17)可以看出回波中有多个LFM信号分量,当m=0的信号分量为主分量,其余为谐波分量时,每个信号分量的中心频率满足(Nm+1)fc-fI,频率范围变成即信号频带被展宽为则在相同脉宽时间内,分量信号的调频率相应变为设采样频率Fs=1.024/2 GHz,M=2, B=10 M Hz,fI=30 M Hz,fd=4 k Hz,信号时宽τ=1μs,拖引率a=1×10-6.图1(a)、(b)分别为目标信号与量化干扰的频谱图,图1 (c)、(d)对应为两信号的时频图.分析干扰信号的时频图如图2所示,可以看出,除主分量外,干扰信号还有两条明显的谐波谱,其中m=-1时对应谐波分量1,m=1时对应谐波分量2.根据上述参数及前述的理论推导,可以计算出谐波分量1的理论中心频率及调频率分别为120.012MHz和-30×1012Hz/s ;谐波分量2的理论中心频率及调频率分别为120.02MHz和50×1012Hz/s.从图2中数据可以粗略计算出谐波分量1的中心频谱及调频率分别为-120.7MHz和-30.1×1012Hz/s,谐波分量2的中心率及调频率分别为120.7MHz和49.12×1012Hz/s,与理论值大致相符.

需要注意,当M较大时,根据式(17)可以发现最大的谐波分量有可能落在采样带宽之外,在干扰信号中将检测不到谐波分量.2.2 参数匹配检测

图2 量化干扰信号的时频图

根据上节分析可知,当雷达没有受到DRFM有源欺骗干扰时,雷达回波中仅有目标回波一个LFM信号分量;当雷达受到DRFM有源欺骗干扰时,雷达回波中会有多个LFM信号分量.而LFM信号在不同的分数阶傅里叶变换域上会呈现出不同的能量聚集性,同时分数阶傅里叶作为一维的线性变换,在处理多分量信号时可以避免交叉项的干扰,因此笔者采用分数阶傅里叶方法来检测雷达回波中多分量LFM信号.

LFM信号x(t)的p阶分数阶傅里叶变换定义为[14]

式中,变换核Kp(t,u)为

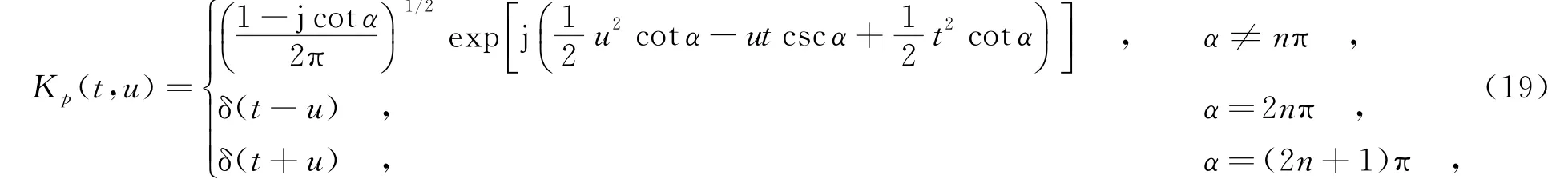
检测未知LFM信号的基本原理是:以旋转角α为变量,对观测信号连续进行分数阶傅里叶变换,形成信号能量在参数(α,u)平面上的二维分布,在此平面上按阈值进行峰值点的二维搜索即可实现信号的检测.而雷达回波中LFM信号分量的幅度受sinc函数调制,差异较大,在信噪比较低的条件下,噪声的起伏可能会影响弱谐波分量峰值点的检测.同时,在实际电磁检测环境中,雷达回波中除了目标回波和欺骗干扰外,还有可能包含来自其他辐射源的未知信号,因此,仅通过检测雷达回波中是否存在多分量LFM信号,并不能有效可靠识别DRFM有源欺骗干扰.

但是从2.1小节的分析可得出干扰信号谐波分量的中心频率及调频率满足一定的规律.为表述方便,令 LFM信号分量参数为其中表示在量化位数为M,N=2M条件下的谐波分量的调频率为相同条件下的谐波分量的中心频率,则有

由式(20)可以得出,干扰信号谐波谱的中心频率是由干扰机量化位数M和fc决定的,其中fc=fI+ fd.干扰信号的调频率由M和雷达发射信号调频率μ决定.实际环境中,并不知道干扰机的量化位数,也无法获知干扰机下变频频率fI,但可以得到参数μ及典型DRFM干扰机的量化位数[15].对于参数,由于受目标多普勒频率、雷达接收机下变频频率以及干扰机下变频频率fI调制,不易计算.对于谐波调频率,在给定典型干扰机量化位数条件下,可以结合已知参量μ计算出.谐波分量的幅度受sinc函数调制,公式(17)表明m=±1时取到最大和次大谐波分量.因此,应建立量化位数为1～4 bit条件下的谐波频谱参数库,其中m=±1,N=21,22,23,24.

文中检测方法的基本思路为:利用分数阶傅里叶变换在(α,u)平面上二维搜索LFM信号并估计参数,如果在雷达回波中检测出多分量LFM信号并且估计出的参数)与参数库)中的某一组参数匹配,就可以判定该雷达受到DRFM干扰机的干扰.这一方法的步骤可表示为:

(2)多分量LFM信号参数估计[14],在(α,u)二维平面上进行搜索,由最大峰值点的位置估计出最强信号分量相应的参数设计中心频率为的窄带滤波器,选择适当带宽,在u域内按尖峰作遮盖处理,滤除最强信号分量.

(4)重复步骤(2)、(3),直到剩余信号中所有的信号分量的幅度均低于某一预定的阈值.将所有估计得到的LFM信号分量的调频率参数与干扰信号谐波参数库进行二维匹配,其具体过程为:先将估计参数与进行匹配,若误差小于设定门限,再将该参数与进行匹配,若误差也小于门限,则可判定雷达回波中存在干扰信号,并且可估计出干扰机量化位数M=1,匹配检测过程结束.如有没有参数满足,则继续与进行匹配,直到遍历完所有参数库中的谐波参数,并做出检测判决.

3 仿真实验

仿真实验条件如下:根据目前典型欺骗干扰机结构,可设DRFM量化位数M=2,DRFM中频FI=30 M Hz,采样频率Fs=1.024/2 GHz,目标多普勒频率fd=4 k Hz.假设检测环境中有两个未知LFM信号分量(可能来自其他辐射源的无意干扰),幅度为雷达发射信号的1/10～1/5倍之间,调频率在±10μ间随机分布.噪声n(t)是服从n～N(0)分布的零均值复高斯白噪声.雷达发射信号为线性调频信号,带宽B=10 M Hz,脉宽τ=1μs.定义信噪比SNR=干噪比JNR=为干扰信号,强度一般是信号强度的1.3～1.5倍,因而可设定JNR=SNR+1.5dB.

图3 分数阶傅里叶变换域上的信号分离

图3给出了雷达回波在分数阶傅里叶变换域上的能量分布.其中,图3(a)表示雷达回波为目标回波与两个未知LFM信号叠加情形下的分数阶傅里叶变换结果,信噪比为10 d B;图3(b)为相同信噪比下回波中同时存在目标回波与干扰信号以及未知LFM信号的分数阶傅里叶变换结果.在上述两种仿真条件下,雷达回波中除主分量外,应该还有其余信号分量,由于幅度差异较大,图3(a)和图3(b)中显示其他分量完全被主分量信号“淹没”.而图3(c)和图3(d)分别为图3(a)和图3(b)情形下抑制了主分量信号后(α,u)平面上的信号能量分布.从图3(c)中可以看出滤除主分量后,回波中还有两个明显的LFM信号分量,而图3(d)中出现至少4个LFM信号分量.分析可知图3(c)中的信号分量为仿真条件中假设的可能来自其他辐射源的两个信号,图3(d)中除了这两个信号分量,其余为有源欺骗干扰信号产生的谐波信号分量.

上述仿真表明,在实际检测环境中,通过检测雷达回波中的多分量LFM信号,并不能有效地检测有源欺骗干扰,需要进一步估计各分量的参数,并与参数库进行匹配分析,才能有效可靠检测出有源欺骗干扰.计算作为参数库,如表1所示.

表1 干扰信号谐波调频率参数库(×1012Hz/s)

表2是在有无欺骗干扰条件下雷达回波检测到的LFM信号分量调频率估计值,分别对应图3(c)和图3 (d)两图.参数估计精度与搜索角度步长有关,根据参数估计精度,设定合适匹配门限,分析发现表2中的无欺骗干扰时所估计的信号分量1、信号分量2的调频率与表1中任何M值下的调频率都不匹配.而在有欺骗干扰时估计的信号分量2与信号分量3能够与参数库中M=2时的调频相匹配,因此可以在复杂检测环境中检测出有欺骗干扰信号,同时还可以估计出干扰机的量化位数M.

表2 雷达回波中信号分量调频率估计值(×1012Hz/s)

图4为信噪比从-15 d B到15dB,每个信噪比下仿真1 000次的干扰信号检测性能曲线.由图中可以看出,在雷达回波中同时存在目标回波和欺骗干扰信号条件下,该方法在0dB左右仍能达到约0.8的正确检测率.因此对于波门拖引干扰,该方法能够在波门捕获期就有效检测干扰信号,使雷达更及时地采取抗干扰措施,保证对目标的正确跟踪.值得说明的是,目前关于干扰检测方法大多是基于模型的,因此算法之间不具有可移植性.干扰机量化特性是固定存在的,与利用干扰信号的幅度波动差异检测方法相比较,文中提出的方法能稳定可靠地提取到干扰与目标信号的差异.

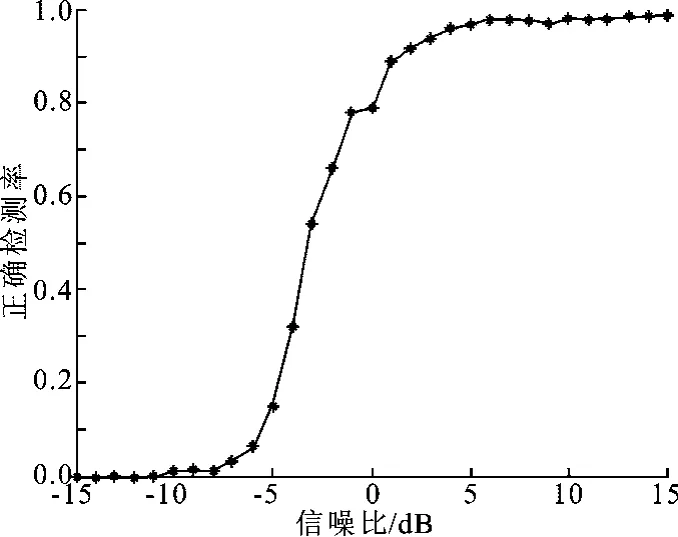
图4 干扰检测性能曲线

4 结束语

有源欺骗干扰因其与雷达发射信号有很强的相干性而难以检测,笔者根据DRFM转发式欺骗干扰存在谐波效应的事实,推导出线性调频干扰信号的频谱特征规律,并建立干扰信号谐波谱调频率参数库.在此基础上提出了一种基于调频率匹配的有源欺骗干扰检测方法.该方法先检测并估计雷达回波中LFM信号分量的调频率参数,通过将估计得到的调频率与参数库进行匹配分析来实现干扰信号的检测.由于LFM信号调频率受环境影响小,因此该方法能在较低信噪比下有效检测出干扰信号.仿真结果表明,该方法能在波门内同时存在目标回波和DRFM转发干扰时有效检测出干扰信号,可使雷达更及时地采取抗干扰措施,在实际应用中有很好的参考价值.同时,随着抗干扰能力较强的捷变频、编码、混合脉冲等雷达发射波形的采用,对复杂波形干扰信号的量化特性将在笔者后继的工作中进行深入研究.

[1]Bandiera F,Farina A,Orlando D,et al.Detection Algorithms to Discriminate Between Radar Targets and ECM Signals [J].IEEE Transactions on Signal Processing,2010,58(12):5984-5993.

[2]Greco M,Gini F,Farina A.Radar Detection and Classification of Jamming Signals Belonging to a Cone Class[J].IEEE Transactions on Signal Processing,2008,56(5):1984-1993.

[3]Zhang Jindong,Zhu Daiyin,Zhang Gong.New Antivelocity Deception Jamming Technique using Pulses with Adaptive Initial Phases[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1290-1300.

[4]Li Jianxun,Shen Qi,Yan Hai.Signal Feature Analysis and Experimental Verification of Radar Deception Jamming [C]//IEEE CIE International Conference on Radar.Piscataway:IEEE,2011:230-233.

[5]孙光才,周峰,邢孟道,等.虚假场景SAR欺骗式干扰技术及实时性分析[J].西安电子科技大学学报,2009,36(5): 813-816.

Sun Guangcai,Zhou Feng,Xing Mengdao,et al.Deception-jamming Technology Against the SAR Based on the Deceptive Scene and Real-time Analyses[J].Journal of Xidian University,2009,36(5):813-816.

[6]杨伟宏,陈永光,王涛.对波形捷变SAR的间歇采样快/慢时间调制干扰[J].系统工程与电子技术,2012,34(12): 2456-2462.

Yang Weihong,Chen Yongguang,Wang Tao.Intermittent Sampling Jamming Against Waveform Agile SAR Modulated in Fast Or Slow Time[J].Systems Engineering and Electronics,2012,34(12):2456-2462.

[7]Olivier K,Cilliers J E,du Plessis M.Design and Performance of wideband DRFM for radar test and evaluation[J]. Electronics Letters,2011,47(14):824-825.

[8]Olivier K,Cilliers J E.Design Aspects and Characterized Performance of a Wideband DRFM for Radar Test and Evaluation[C]//IET International Conference on Radar Systems.Stevenage:IET,2012:1-4.

[9]Greco M,Gini F,Farina A.Combined Effect of Phase and RGPO Delay Quantization on Jamming Signal Spectrum [C]//IEEE International Radar Conference.Piscataway:IEEE,2005:37-42.

[10]Greco M,Gini F,Farina A,et al.Effect of Phase and Range Gate Pull-off Delay Quantization on Jammer Signal[J]. IEE Proceedings-Radar,Sonar and Navigation,2006,153(5):454-459.

[11]Berger S D.Digital Radio Frequency Memory Linear Range Gate Stealer Spectrum[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(2):725-735.

[12]Berger S D.The Spectrum of a Digital Radio Frequency Memory Linear Range Gate Stealer Electronic Attack Signal [C]//Proceedings of the IEEE National Radar Conference.Piscataway:IEEE,2001:27-30.

[13]孙闽红,唐斌.距离-速度同步拖引欺骗干扰的频谱特征分析[J].系统工程与电子技术,2009,31(1):83-85.

Sun Minhong,Tang Bin.Analysis of the Frequency Spectrum of a Simultaneous Range-gate-pull-off and Velocity-gatepull-off Jamming Signal[J].Systems Engineering and Electronics,2009,31(1):83-85.

[14]陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009.

[15]Streetly M.Jane’s Radar and Electronic Warfare Systems 2008-2009[M].London:Jane’s Information Group,2008.

(编辑:王 瑞)

Method for detecting DRFM deception jamming based on LFM rate matching

LU Yunlong,LI Ming,YAN Yan
(National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China)

For detecting linear frequency modulated(LFM)active deception jamming,a novel approach is outlined based on LFM rate matching of the jamming harmonic components.Utilizing the harmonic effect generated from a digital radio frequency memory(DRFM),the feature of the harmonic spectrum is analyzed and an LFM rate base of the jamming is established first.Then the Fractional Fourier Transform(Fr FT)is employed to detect LFM components in the radar echo when both the target echo and the jamming signal are co-existent in a range gate.After that the LFM rates of the detected LFM signal are estimated and compared with the LFM rate bank to achieve jamming detection.Validity of the method is verified by simulation results.

DRFM quantization;active deceptive jamming;Fr FT;parameter estimate

TN974

A

1001-2400(2014)05-0067-07

2013-05-21< class="emphasis_bold">网络出版时间:

时间:2014-01-12

国家部委预研基金资助项目(9140A07020913DZ01001);博士学科点科研专项基金资助项目(20110203110001);航空科学基金资助项目(20110181006)

卢云龙(1986-),男,西安电子科技大学博士研究生,E-mail:yllu@stu.xidian.edu.cn.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.012.html

10.3969/j.issn.1001-2400.2014.05.012