一种新的未知杂波环境下的PHD滤波器

李翠芸,江 舟,2,姬红兵

(1.西安电子科技大学电子工程学院,陕西西安 710071; 2.中国人民解放军95972部队,甘肃酒泉 735018)

一种新的未知杂波环境下的PHD滤波器

李翠芸1,江 舟1,2,姬红兵1

(1.西安电子科技大学电子工程学院,陕西西安 710071; 2.中国人民解放军95972部队,甘肃酒泉 735018)

针对多目标跟踪中概率假设密度(PHD)滤波器在杂波模型与先验知识不匹配情况下滤波性能急剧下降的缺点,将增广状态空间引入PHD滤波器,提出了一种新的未知杂波环境下的PHD滤波器.该滤波器利用增广状态空间区分目标状态空间与杂波状态空间,通过量测对杂波模型进行估计,不需要杂波先验知识,避免了因杂波强度的先验知识选择不当而造成PHD滤波器跟踪性能下降的问题.仿真结果表明,该算法在未知杂波环境下,具有稳定的跟踪效果;在保证实时性的前提下,其跟踪精度与传统PHD滤波器在杂波模型匹配情况下相当.

多目标跟踪;概率假设密度;未知杂波;增广状态空间

传统的多目标跟踪算法需要进行数据关联计算[1],运算量较大,影响了多目标跟踪的实时性.由于随机有限集(Random Finite Set,RFS)统计理论不需要进行复杂的数据关联计算,而引起学术界和工程应用界的高度重视.文献[2]提出的概率假设密度(Probability Hypothesis Density,PHD)滤波算法,并不计算全体目标的联合后验概率分布,而是以递归的形式去估计RFS变量的一阶统计量,通过对目标集合和观测集合的处理,将复杂的多目标状态空间的运算转换为单目标状态空间的运算.在保证算法实时有效性的同时,也提高了多目标的跟踪精度,具有很高的理论研究价值和应用价值.PHD滤波的优点在于,它是在单目标的状态空间中操作的,有效避免了复杂的数据关联组合问题.

在传统的PHD滤波中,杂波已知且被建模为一个泊松点过程,它的所有特征可以用强度信息λc(zk)来描述[2-3],其中,λ表示每一时刻杂波的平均数目,c(zk)表示k时刻杂波的密度函数.当所采用的假设杂波模型和实际杂波模型显著不同时,传统PHD滤波器的性能会急剧下降[3].文献[4]提出了一种对未知杂波进行估计的PHD滤波算法,该算法利用有限混合模型描述杂波的密度函数,通过期望极大化算法[5]或马尔科夫链蒙特卡罗算法[6]估计该混合模型参数.但该算法仅适用于杂波数远大于目标数的情况.并且该方法在仿真实验的实际参数设置中,通常假设杂波数λ已知,主要估计杂波空间分布概率密度函数c(zk).文献[7-8]利用混合状态空间模型得到杂波模型估计,但是在实际应用中一般只估计杂波数,其空间分布概率密度函数c(zk)先验已知,且该文献中的仿真实验结果并不理想.文献[9]在文献[7-8]的基础上对混合势分布进行了改进,可降低目标漏检率,但会出现较大的判决延迟.文献[10-11]从泊松点过程理论出发,提出了强度滤波器.该滤波器假设多目标跟踪模型服从泊松点过程,通过对泊松点过程的强度进行Bayes递归,直接推导出概率密度函数递推公式.强度滤波器中利用增广状态空间区分目标状态空间与杂波状态空间,通过量测对杂波模型进行估计,不需要杂波先验知识.文献[12-13]给出了强度滤波器的序贯蒙特卡罗(Sequential Monte Carlo,SMC)方法实现.因需要先验设定较多的系统参数,目前人们对强度滤波器在多目标跟踪的实际应用和研究还较少.

笔者提出了一种未知杂波环境下的PHD滤波器,引入了强度滤波器中的增广状态空间概念,利用量测数据建立杂波模型,不需要杂波的先验知识.仿真实验验证了该算法的跟踪性能和精度,避免了因杂波强度的先验知识选择不当而造成PHD滤波器性能下降的问题.

1 PHD滤波器

随机有限集是对多目标状态和观测的一种有效的表示方法.尽管随机有限集已经拥有严格的数学基础,但由于基于随机集的最优多目标贝叶斯滤波要解决高维的积分求和问题,计算比较复杂.概率假设密度滤波是基于随机集的方法,是最优贝叶斯多目标滤波方法的另外一种选择.为了获得迭代的闭合形式,假设在预测和更新过程是泊松点过程,这种迭代能准确和完全地描述动态泊松点过程的期望值.PHD是定义在目标活动空间里的函数,但它并不是一个概率密度函数,它是正的、可积的,但积分值不一定为1.它传播概率假设密度函数,即多目标后验概率的一阶矩,从中可以提取目标数目及每个目标的状态.在状态空间的任意区域S对PHD积分可以得该积分区域的目标数期望值,其峰值点为各个目标状态.

其中,Sk(Xk-1)表示在k时刻存活的目标随机集,Bk(Xk-1)表示由Xk-1中的目标衍生出的新的目标随机集, Γk表示在k时刻出现的新生目标随机集.

其中,Ek(Xk)表示由Xk产生的观测值随机集,Kk表示杂波或虚警随机集.

设Dk(x)和Dk|k-1(x)分别表示k时刻多目标后验概率密度pk(X)和预测概率密度pk|k-1(X)的PHD.在满足文献[14]假设的条件下,目标随机集的PHD迭代递归可表示为

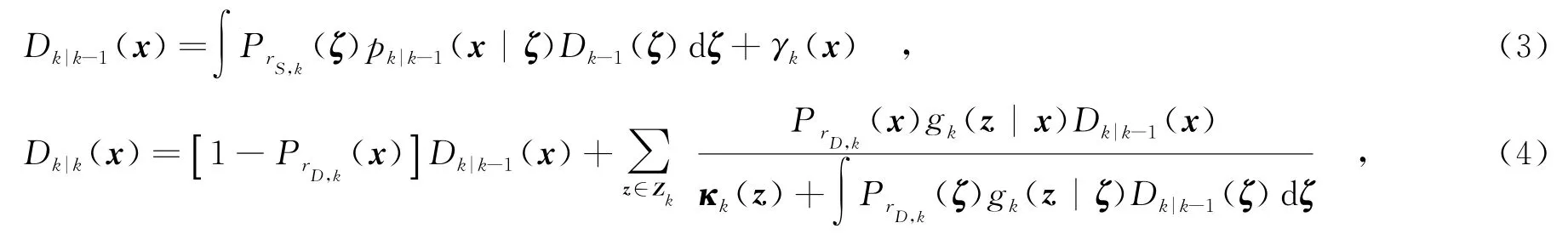
其中,PrS,k(ζ)表示k-1时刻状态为ζ的目标在k时刻的存活概率,γk(·)表示k时刻新生目标随机集Γk的PHD,pk|k-1(x|ζ)表示k时刻目标转移概率,PrD,k(x)表示k时刻状态为x的目标的检测概率,κk(·)表示k时刻杂波随机集Kk的PHD,gk(z|x)表示k时刻目标的量测似然函数,Zk表示k时刻的包括所有量测的随机集.

2 未知杂波环境下的PHD滤波器

2.1 未知杂波环境下PHD的原理

PHD滤波器的理论基础是随机有限集,其递归运算的是PHD,也有人称为后验强度密度,它是多目标后验密度的一阶矩;强度滤波器是由泊松点过程推导出的,其递归运算的是泊松点过程的强度,从本质上来说,PHD滤波器是一种特殊的强度滤波器,即杂波模型与新生目标强度先验已知的强度滤波器[10-11].在理想情况下,目标观测值与目标状态一一对应,在实际情况中,往往有部分量测没有与之对应的状态.这里根据PHD滤波器与强度滤波器的相似性,从强度滤波器引入增广状态空间X+=X∪φ来表示这种情况,其中,X表示目标状态空间,φ表示虚假目标(即杂波)的状态.引入增广状态空间后,PHD的一些参数就会从目标状态空间扩展到增广状态空间,需再定义几个状态转移函数及似然函数,推导分析如下.

假设Dk(φ)和Dk|k-1(φ)分别表示k时刻杂波后验概率密度pk(φ)和杂波预测概率密度pk|k-1(φ)的PHD.未知杂波环境下PHD迭代递归可用如下公式表示.

增广状态空间随机集PHD的预测可表示为

其中,pk|k-1(φ|ξ)表示k时刻虚假目标(杂波)的新生概率,pk|k-1(φ|φ)表示k时刻虚假目标(杂波)的转移概率,其余参数与PHD预测公式中参数相同.

增广状态空间随机集PHD的更新可表示为

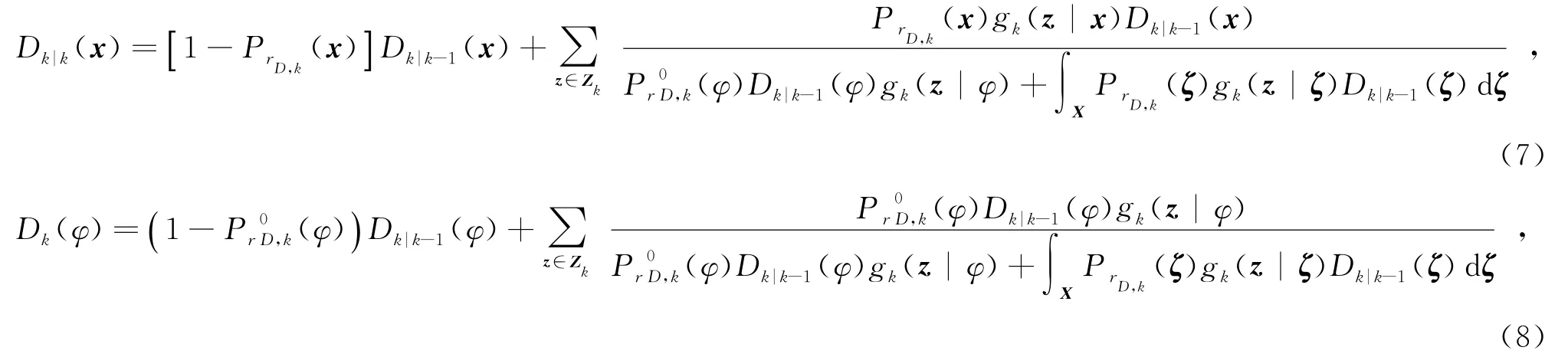
2.2 未知杂波环境下PHD滤波器的SMC实现

SMC实现的具体步骤如下:

(1)初始化.假设目标数为N0,每个目标采样N个粒子,则初始粒子数L0=NN0.给定多目标先验概率为p0(X0),对初始状态随机集X0采样,得到粒子～p0(X0),粒子对应权值为

(2)预测目标PHD.对存活目标的建议分布qk(·|,Zk)和新生目标的建议分布pk(·|Zk)进行采样.设k-1时刻有Lk-1个粒子,k时刻新生目标的蒙特卡罗采样粒子数为Jk.

对i=1,2,…,Lk-1,采样～qk(·|,Zk),存活粒子的预测权值为

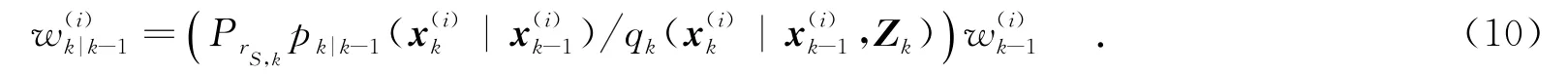
对i=Lk-1+1,2,…,Lk-1+Jk,采样～pk(·|Zk),新生粒子的预测权值为

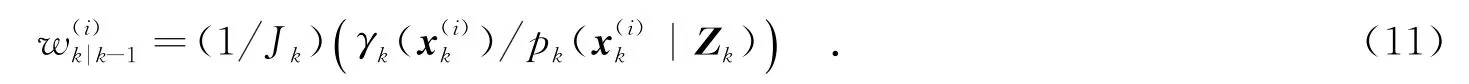
(3)预测杂波强度为

(4)目标更新.对i=1,2,…,Lk-1+Jk,更新粒子权值为

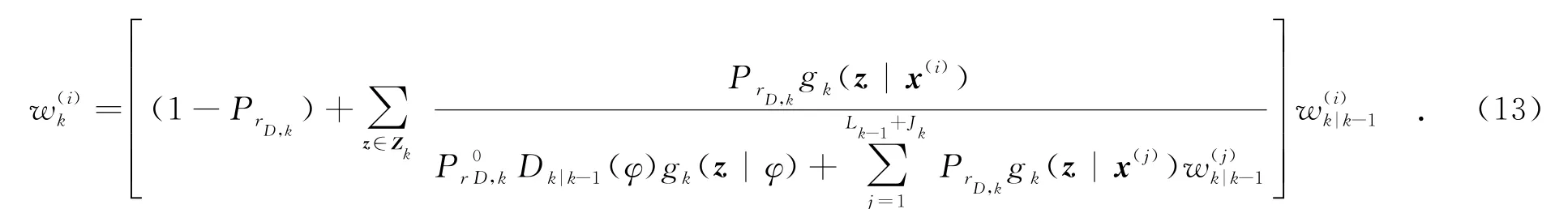
(5)杂波强度更新为

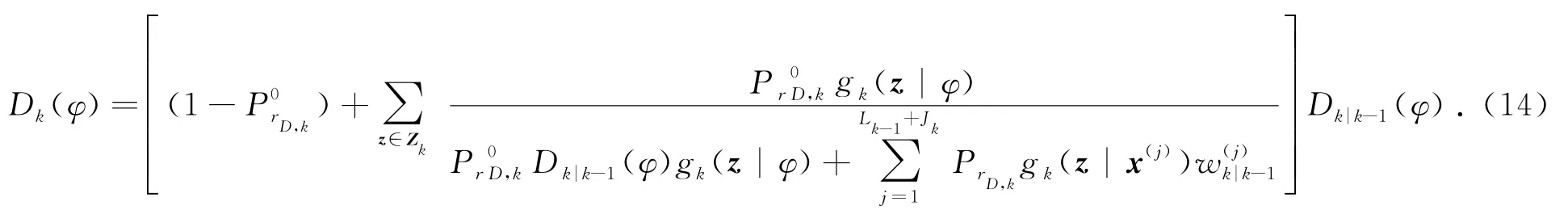
(6)估计目标数为

其中,int(·)表示四舍五入取整.

(8)目标状态提取.根据估计目标数将重采样后的粒子进行聚类,聚类中心即为目标状态估计.

3 仿真实验与分析

对文中所提的未知杂波环境下新PHD滤波器(NPHD)与传统PHD滤波器进行性能仿真对比实验.由于多目标跟踪问题不仅要估计目标的数目,还要估计各目标的状态,因此可利用最优子模式分配(OSPA)距离评价准则来评价多目标跟踪算法的跟踪精度,其定义式[15]为

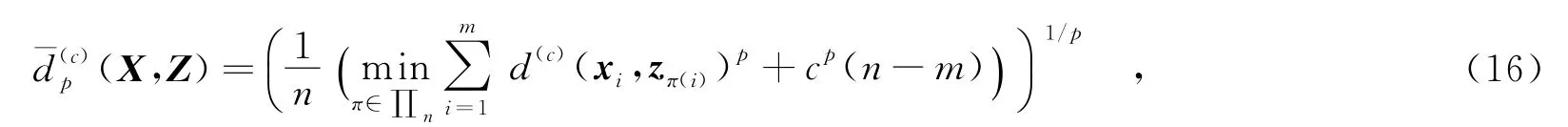
其中,X和Z表示任意子集,其维数分别为m和n,且m≤n;d(c)(x,z)=min{c,d(x,z)}(c＞0);Πk表示{1,2,…,k}的所有排列组成的集合.若m＞n,则有

文中描述的所有算法的目标运动模型均为线性模型,目标的状态向量其中,表示目标的位置,表示目标的速度.运动方程为

系统的观测方程为

新生目标随机集的强度函数为

目标存活概率PS=0.95,目标检测概率Pd=0.98,观测区域为[-100,100]m×[-100,100]m,时间为40帧,采样周期Δ=1 s,粒子数目为500,蒙特卡罗仿真次数为100,OSPA距离参数p=2,c=50.杂波均匀分布于量测空间,量测杂波的数量可以通过泊松分布的平均值AρA表示,其中,A表示观测区域的面积,ρA表示杂波密度.

图1展示了目标的真实运动轨迹.目标1在第1秒新生,在第8秒消亡;目标2在第8秒新生,在第26秒消亡;目标3在第12秒新生,在第38秒消亡;目标4在第26秒新生,在第40秒消亡.

图1 目标真实运动轨迹

在低、中、高3种杂波密度的情况下对文中所提的NPHD滤波器与传统PHD滤波器进行比较,其中低、中、高3种杂波密度对应的值分别为:ρA=2.5×10-5,ρA=1.25×10-4,ρA=2.5×10-4.实验中,传统PHD滤波器先验杂波模型与中杂波密度环境匹配,文中所提的NPHD滤波器杂波密度未知.

图2给出了NPHD滤波器和PHD滤波器在3种杂波环境下的目标数估计均值及OSPA距离.从图2可以看出,文中提出的NPHD滤波器在低、中、高杂波环境下均能较为准确地估计出目标数,且保持较小的跟踪误差,跟踪性能稳定.传统PHD滤波器在假设杂波模型条件下与实际杂波分布相匹配情况下,跟踪性能较好,如图2(c)、图2(d)所示.PHD滤波器在假设的先验杂波模型与实际的杂波分布不匹配情况下性能会急剧下降,如图2(a)、图2(b)、图2(e)和图2(f)所示.

图2 两种滤波器在3种杂波环境下的目标数估计及OSPA距离

表1给出了文中提出的NPHD滤波器与传统PHD滤波器分别在低、中、高杂波密度情况下,100次蒙特卡罗实验的平均OSPA距离误差及每帧所需的时间.

表1 两种算法的OSPA距离及所耗时间对比

通过表1的数据可以看出,文中提出的NPHD滤波器比传统PHD滤波器的计算所耗时间要多20%左右,但是,在PHD滤波器的先验杂波模型与实际的杂波模型匹配的条件下,文中提出的NPHD滤波器跟踪性能和传统PHD滤波器相当;而在其先验杂波模型与实际的杂波模型不匹配的条件下,文中提出的NPHD滤波器的性能远远超过PHD滤波器的性能.

4 结束语

提出了一种新的未知杂波先验模型的PHD滤波器,通过量测数据对杂波状态空间进行估计,并修正了增广状态空间PHD滤波的预测与更新方程.采用数值仿真方法与传统PHD滤波器加以比较分析.实验结果表明,该滤波器具有稳定的跟踪性能.该方法可以处理不同杂波密度下的多目标跟踪,其性能与杂波模型匹配条件下的传统PHD滤波相当.由于该滤波器增加了对杂波的估计,因此在计算量上略有增加.

[1]王宝树,李芳社.基于数据融合技术的多目标跟踪算法研究[J].西安电子科技大学学报,1998,25(3):269-272.

Wang Baoshu,Li Fangshe.The Research on Multiple Targets Tracking Based on the Data Fusion Technique[J].Journal of Xidian University,1998,25(3):269-272.

[2]Mahler R.Statistical Multisource-multitarget Information Fusion[M].Boston:Artech House Publishers,2007.

[3]杨柏胜,姬红兵,高小东.随机集粒子滤波的快速被动数据关联算法[J].西安电子科技大学学报,2010,37(4):655-659.

Yang Baisheng,Ji Hongbing,Gao Xiaodong.Fast Passive Data Association Algorithm Base on the Random Set Particle Filter[J].Journal of Xidian University,2010,37(4):655-659.

[4]Lian Feng,Han Chongzhao,Liu Weifeng.Estimating Unknown Clutter Intensity for PHD Filter[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(4):2066-2078.

[5]Zhou Xin,Jiang Ju,Wang Congqing.Maximum Likelihood Parameter Estimation for G0 Distribution via EM Algorithm [C]//Proceedings of the 10th International Bhurban Conference on Applied Sciences and Technology.Washington: IEEE,2013:89-93.

[6]Watanabe R,Okamura H,Dohi T.An Efficient MCMC Algorithm for Continuous PH Distributions[C]//Proceedings of the Winter Simulation Conference.New York:IEEE,2012:1-12.

[7]Mahler R,El-Fallah A.CPHD and PHD Filters for Unknown Backgrounds,PartⅢ:Tractable Multitarget Filtering in Dynamic Clutter[C]//Proceedings of SPIE:7698.Bellingham:SPIE,2010:76980F.

[8]Mahler R,Vo B T,Vo B N.CPHD Filtering with Unknown Clutter Rate and Detection Profile[J].IEEE Transactions on Signal Processing,2011,59(8):3497-3513.

[9]Zheng Xuetao,Song Liping.Improved CPHD Filtering with Unknown Clutter Rate[C]//Proceedings of the 10th World Congress on Intelligent Control and Automation.Piscataway:IEEE,2012:4326-4331.

[10]Streit R,Stone L.Bayes Derivation of Multitarget Intensity Filters[C]//Proceedings of the International Conference on Information Fusion.Piscataway:IEEE,2008:4632414.

[11]Streit R.Poisson Point Processes:Imaging,Tracking,and Sensing[M].Heidelberg:Springer,2010.

[12]Schikora M,Gning A,Mihaylova L,et al.Box-particle Intensity Filter[C]//9th IET Data Fusion and Target Tracking Conference.Stevenage:IET,2012:1-6.

[13]Schikora M,Koch W,Streit R,et al.Advances in Intelligent Signal Processing and Data Mining[M].Heidelberg: Springer,2013:55-87.

[14]Vo B N,Singh S,Doucet A.Sequential Monte Carlo Methods for Multitarget Filtering with Random Finite Sets[J]. IEEE Transactions on Aerospace and Electronic Systems,2005,41(4):1224-1245.

[15]He Xiaofan,Tharmarasa R,Kirubarajan T,et al.A Track Quality Based Metric for Evaluating Performance of Multitarget Filters[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):610-616.

(编辑:齐淑娟)

Novel PHD filter in unknown clutter environment

LI Cuiyun1,JIANG Zhou1,2,JI Hongbing1
(1.School of Electronic Engineering,Xidian Univ.,Xi’an 710071,China; 2.Unit 95972,PLA,Jiuquan 735018,China)

Aiming at improving the poor performance of the Probability Hypothesis Density(PHD)filter when the clutter model and the prior knowledge are mismatched,a novel PHD filter into which we introduce the augmented state space and which is used under the unknown clutter circumstance is proposed in this paper.The proposed filter can distinguish the target state space and the clutter state space by the augmented state space.Using the estimate of the unknown clutter model from the measurement,the filter can avoid the tracking performance reduction caused by the improper model selection of the unknown clutter.Simulation results show that the proposed algorithm can achieve a stable tracking performance under the unknown clutter circumstance and a tracking accuracy equal to that of the conventional PHD filter used in the unknown clutter circumstance in the real-time context.

multitarget tracking;probability hypothesis density;unknown clutter;augmented state space

TN953

A

1001-2400(2014)05-0018-06

2013-06-13< class="emphasis_bold">网络出版时间:

时间:2014-01-12

国家自然科学基金资助项目(61372003);国家自然科学基金青年基金资助项目(61101246,61301289);中央高校基本科研业务费专项资金资助项目(K5051202014);国家留学基金资助项目(201206965015)

李翠芸(1976-),女,副教授,博士,E-mail:cyli@xidian.edu.cn.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.004.html

10.3969/j.issn.1001-2400.2014.05.004