阵列信号降采样低秩矩阵的恢复方法

杨 东,廖桂生,朱圣棋,王 凯

(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071; 2.中国人民解放军61251部队,河北秦皇岛 066102)

阵列信号降采样低秩矩阵的恢复方法

杨 东1,廖桂生1,朱圣棋1,王 凯2

(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安 710071; 2.中国人民解放军61251部队,河北秦皇岛 066102)

矩阵填充可以有效恢复阵列信号降采样数据,从而得到等效的全采样回波信号.然而,现有基于矩阵填充的阵列波达方向估计方法要求回波数据在不同快拍下随机选择采样序列,以满足采样数据的随机性.当部分阵元在整个观测时间内关闭或损坏时,上述方法将失效.因此,笔者提出了一种改进的降采样数据恢复方法,利用阵元间的相关特性,将单快拍下的信号矢量变换到一个等效的低秩矩阵,继而通过求解该矩阵的最小核范数,实现对缺失数据的有效估计.仿真结果表明,该方法可以有效恢复降采样数据,抑制噪声,提高波达方向的估计性能.

阵列信号;矩阵填充;低秩矩阵;波达方向估计

阵列信号处理被广泛应用于雷达、声纳、导航和通信领域,基于子空间的方法(如MUSIC、ESPRIT等)可以实现角度的超分辨估计[1].然而,随着阵列规模的扩大,系统功耗和存储空间会逐步增加.当来波信号个数较少时,回波数据对信息量的需求相对较小,这时对整个阵列进行全采样会存在冗余信息.因此,合理地降低采样阵元数目,可以有效提高系统的工作效率.现有基于内插或学习的方法[2-3]虽然可以估计采样数据,但十分依赖于先验知识.

矩阵填充理论(Matrix Completion,MC)[4-8]是继压缩感知后,对稀疏信号进行恢复的另一种有效方法,它旨在将一个低秩不完整的矩阵,利用其元素间的相关性,恢复出矩阵的全部数据.当来波信号稀疏时,阵列接收回波满足很好的低秩特性,因此在没有先验知识的条件下,可以通过MC方法对降采样后的缺失数据进行有效估计.由于整个恢复过程的本质在于利用数据间的相关性,因此对于任何一个降采样数据,如果其中某一行或某一列整体没有被采样,那么就意味着缺失数据没有任何可利用的信息,将不能得到有效的恢复.这就要求阵列信号在降采样过程中,每个快拍下采样阵元的选取要满足随机性,也就是说采样点随机分布在整个回波数据中[5].基于这样的信号模型,文献[9-10]利用MC方法对全数据进行恢复,从而得到了等效的全采样信号.

但实际的降采样方法应该是在整个接收时间内选择性地关闭部分阵元(类似于部分阵元损坏).在这种模型下,由于对应于这些未采样阵元的回波数据不包含任何信息,因此阵列信号将不能按照上述方法整体恢复.为了解决这一问题,笔者提出一种有效的方法,利用等距线阵数值间的等比特性,将单次快拍下的信号改写为一个等效低秩矩阵.在该等效低秩矩阵中,采样点重新分布,满足了采样数据的随机性,所以该信号模型可以通过MC得到有效估计.同时,利用求解过程中的去噪特性,可以进一步提高波达方向的估计性能,最终通过仿真结果验证笔者方法的有效性.

1 阵列信号波达方向模型

阵列模型如图1所示,一个均匀等距线阵包含M个阵元,其接收信号为

其中,X(t)=[x(t1),…,x(tN)],是N个快拍下的接收信号, s(t)是信号的幅度,N(t)是高斯随机白噪声,k个远场窄带信号的导向矢量表示为A(θ)=[a(θ1),a(θ2),…,a(θk)],其中θi即信号波达方向(DOA)估计问题中所需求解的参量.导向矢量具体写为

其中,d是阵元间距,一般定义为载波波长λ的一半.假设信号采样快拍数足够充分,可以得到回波的协方差矩阵

其中,E表示期望,H表示共轭转置.进一步将其分解为

其中,γi代表了第i个特征值,相应的特征向量为ui.前k个大特征值对应的特征向量{u1,u2,…,uk}定义为信号子空间Us,其补空间为噪声子空间Un.因此,基于MUSIC的DOA估计方法表示为

其尖峰代表了来波信号的估计方向角.

图1 阵列信号模型

2 基于MC的数据恢复方法

由于来波信号在空域具有稀疏性,因此可以选择性地减少采样数据,并利用其冗余信息估计未采样的数值.

2.1 全数据恢复方法

假设降采样后的回波数据X(t)中包含未采样的零值点,协方差矩阵估计存在微小误差,此时基于MUSIC的方法会出现性能损失.将式(1)改写为

可以看出当来波信号个数稀疏时,上述信号在不考虑噪声时满足低秩特性.这样的结构使得我们可以利用矩阵填充方法去恢复丢失的数据,在降采样条件下得到全采样的估计结果.将观测的数据定义为一个全采样数据在子集Ω上的投影,那么接收的信号可以表述为

当这个子集是随机选取时,文献[9-10]提出了基于矩阵填充对全数据进行恢复的方法.实际上,这样的恢复过程是利用了不变的阵列导向矢量和不同快拍下变化的信号幅度,这个关系使得整个数据是一个低秩矩阵,因此未观测的数值可以通过求解下式得到:

值得注意的是,MC理论要求所恢复矩阵必须满足强非相干特性(Strong Incoherence Property)[5],这就意味着,当所恢复矩阵中的某一行或某一列完全没有信息时,该矩阵不能得到有效恢复.因此对于上述恢复模型,所定义的子集需要满足随机性.但这一点在阵列中并不合理,因为降采样模型应该是在整个观测时间内固定选择部分采样阵元,而不是每次快拍下随机选取,在这种情况下,上述方法将不再适用.

2.2 文中方法

对于固定阵元降采样模型,数据结构如图2所示,其中阴影区域表示没有采样信号,此时上述全数据恢复的方法失效.为了解决这一问题,笔者提出一种新的数据恢复方法.回顾式(2)中导向矢量的定义,可以发现在某一个方向θ,其数值满足比值为exp( j2πd(λsinθ)的等比特性.因此利用这一结构特点,将导向矢量矩阵化

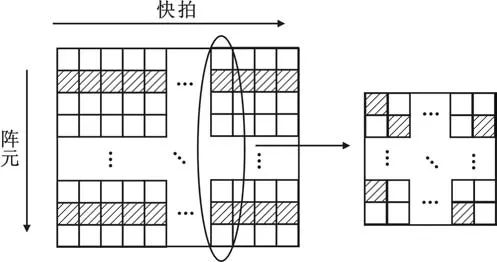
图2 部分阵元降采样数据及其变换方法

阵元的导向矢量本是一个M×1维的向量,在上式中,将其重新写为一个等效的l×m维矩阵,且满足M=l×m.正如上面所说,由于其数值具有等比特性,因此构造的新的矩阵是一个低秩矩阵,如图2中的变化所示.虽然在整个接收时间内有部分阵元没有回波数据,但是在新的矩阵中这些未采样的点被重新排列,类似于在新的矩阵中随机采样.因此经过变化后,可以利用这种新的关系去估计未采样点的数值,最终实现回波数据的有效恢复.将式(6)在某一时刻tm的信号写为

其中,x(tm)是在这一时刻各个阵元的接收信号矢量,进一步将回波和导向矢量改写为矩形形式为

其中,˜x(tm)是x(tm)重写为l×m形式的矩阵.因此降采样信号可以通过求解下式估计

下面进一步分析该方法的去噪性能.由于矩阵填充理论是建立在低秩特性的基础之上的,因此其本身在求解过程中可以降低噪声或者扰动,提高信噪比,但是并不能提高DOA的估计性能.故将式(6)重写为

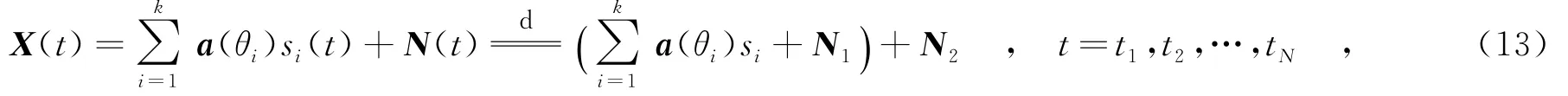
其中,N1是融入信号的噪声部分,N2是与信号不相干的噪声部分,可以认为前一部分将和信号一起构成协方差矩阵中的信号子空间,而后者对其没有影响.由式(5)可以看出,基于子空间的方法其本质是利用导向矢量与信号子空间(或噪声子空间)的正交性去判断来波角度,信号子空间中噪声扰动量的大小将最终决定估计性能.如果按照式(8)对整个阵列降采样后的回波数据进行恢复,仅仅可以降低噪声N2,其本质并不改变信号子空间内的噪声扰动(即N1),因此无益于提高估计性能.

所以,重新考虑文中的处理方法,在某一时刻tm,式(13)变为

其中,N1(tm)是在时刻tm与导向矢量a(θi)相关的噪声,N2(tm)是与a(θi)不相关的噪声.将其改写为如式(11)的形式,即

综上,将单次快拍下的向量变换为一个等效的矩阵,利用其内部的相关性对数据进行恢复,这样的处理方法可以有效估计未采样阵元的信息,但同时也降低了系统可利用的自由度.对于信号的降采样,本身就意味着采样中所包含的信息量具有足够的冗余度,因此该方法不能处理目标数目过多的情况,这也是其不足之处.

3 仿 真

为了验证方法的有效性,本节对阵列回波进行仿真分析.假设由36个阵元构成的等距线阵,接收来波方向分别为-10°和30°的两个远场窄带信号,信噪比为10dB,恢复算法采用文献[12]的增广拉格朗日乘子算法.

首先分析文中方法对数据恢复的性能.随机选择8个阵元在整个观测时间内一直关闭,图3画出了数据恢复后基于MUSIC的DOA估计结果.一般而言,估计结果的峰值越高,可以认为输入信号具有更高的信噪比,或者拥有更多的能量积累,因此这里可以理解为具有更好的数据恢复结果.图3中-20dB的实线是100%数据下的DOA估计结果,而在-5dB的实线是70%数据下的结果,由于其积累能量的减少以及协方差矩阵估计存在误差,性能存在较大损失.在-5dB处的点线是基于全数据MC恢复方法的结果,按照前面的分析,由于其中未采样阵元没有任何可利用信息,因此该方法失效,无法恢复数据,导致其结果相对于70%的数据没有任何改善.相比而言,图3中最下方的点画线是文中方法的结果,可以看出该结果不但可以有效恢复数据,同时可以抑制噪声,提高DOA估计性能.

图4进一步分析文中方法和全数据恢复方法对噪声的抑制能力.为了在同等条件下对比其结果,该实验采用随机降采样方式.从图中可以看出,相比于70%数据的结果,上述两种方法都可以有效地恢复数据,得到更好的DOA估计结果,但是文中方法拥有更高的估计峰值(即归一化后峰值两边更低的旁瓣).图5进一步细化了去噪结果,其中图5(a)是数据恢复后的信噪比,可以看出,此时全数据恢复方法拥有更高的输出信噪比.图5(b)是随后得到的DOA估计峰值结果,然而文中方法却具有更高的峰值.这一结果与前文分析结果相同.由此可以说明,全数据恢复方法仅仅可以降低噪声子空间的能量,但是对结果没有影响,而文中方法可以降低信号子空间中的噪声扰动量,因此最终提高了DOA的估计性能.

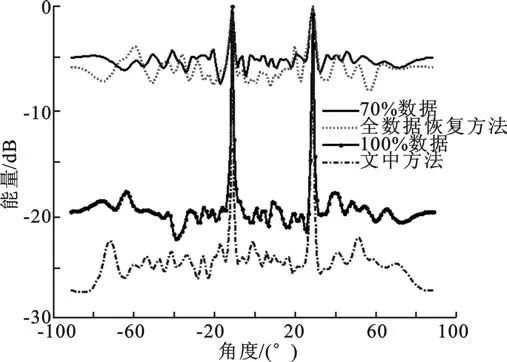
图3 固定阵元降采样下的DOA估计结果

图4 随机降采样下的DOA估计结果

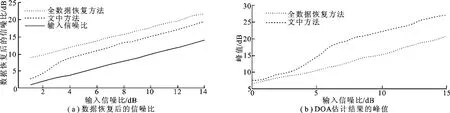
图5 降噪性能分析

图6 不同采样率下信号恢复的均方根误差

图6是不同采样率下的信号恢复结果,其估计值与真实值的均方根误差定义为

可以看出,文中方法和全数据恢复方法的误差始终在同一个数量级,因此在信号个数较少时,并不需要更多的采样数据.其中,图6(a)、图6(c)和图6(e)是阵元个数为36且信号个数k为1、4、7下的情况的情况,图6 (b)、图6(d)和图6(e)是阵元个数为100的情况,不考虑噪声影响.通过横向对比得到,阵元数越多,可利用的信息量越多,则恢复误差越小.同样,随着信号个数的增加,回波数据的秩数变大,误差会相应变大.综上,采样率的增加,阵元个数的增加,以及信号个数的减少都会提高信号的恢复性能.

4 结束语

矩阵填充方法可以有效恢复阵列信号降采样数据,然而当部分阵元关闭或损坏时,基于全数据的恢复方法失效.为此,笔者提出一种改进算法,通过将信号矢量变化为一个等效的低秩矩阵,使得采样点重新随机分布在其中,最终实现对该模型下降采样信号的有效估计.仿真结果表明,该方法在有效恢复降采样数据的同时,达到了降低噪声,提高DOA估计性能的目标.该方法还适用于其他信号模型,从而为基于矩阵填充的数据恢复方法提供了新的思路.

[1]王凌,李国林,刘坚强,等.一种基于数据矩阵重构的相干信源二维侧向新方法[J].西安电子科技大学学报,2013,40 (2):130-137.

Wang Ling,Li Guolin,Liu Jianqiang,et al.New Method for Estimating 2-D DOA in the Coherent Source Environment Based on Data Matrix Reconstruction[J].Journal of Xidian University,2013,40(2):130-137.

[2]Larsson E G,Stoica P.High-resolution Direction Finding:the Missing Data Case[J].IEEE Transactions on Signal Processing,2001,49(5):950-958.

[3]Vigneshwaran S,Sundararajan N,Saratchandran P.Direction of Arrival(DOA)Estimation under Array Sensor Failures Using a Minimal Resource Allocation Neural Network[J].IEEE Transactions on Antennas and Propagation,2007,55 (2):334-343.

[4]Candes E J,Recht B.Exact Matrix Completion via Conves Optimization[J].Foundations of Computational Mathematics,2009,9(6):717-772.

[5]Candes E J,Plan Y.Matrix Completion with Noise[J].Proceedings of the IEEE,2010,98(6):925-936.

[6]Candes E J,Tao T.The Power of Convex Relaxation:Near-optimal Matrix Completion[J].IEEE Transactions on Information Theory,2010,56(5):2053-2080.

[7]郭慧杰,赵保军.基于矩阵填充的小波图像压缩算法[J].系统工程与电子技术,2012,34(9):1930-1933.

Guo Huijie,Zhao Baojun.Wavelet Image Compression Based on Matrix Completion[J].Systems Engineering and Electronics,2012,34(9):1930-1933.

[8]Yan H,Wang R,Li F.Ground Moving Target Extraction in a Multichannel Wide-area Surveillance SAR/GMTI System via the Relaxed PCP[J].IEEE Transactions on Geoscience Remote Sensing,2013,10(3):617-621.

[9]Yerriswamy T,Jagadeesha S N.Fault Tolerant Matrix Pencil Method for Direction of Arrival Estimation[J]. International Journal of Signal and Image Processing,2011,2(3):55-67.

[10]Weng Z,Wang X.Low-rank Matrix Completion for Array Signal Processing[C]//IEEE International Conference on Acoustics,Speech,and Signal Processing.Piscataway:IEEE,2012:2697-2700.

[11]Candes E J,Li X,Ma Y.Robust Principal Component Analysis[J].Journal of the ACM,2011,58(3):11.

[12]Lin Z,Chen M,Ma Y.The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-rank Matrices[R].Technical Report,UIUC-ENG-09-2215,2009.http://arxiv.org/abs/1009.5055.

(编辑:王 瑞)

Improved low-rank recovery method for sparsely sampling data in array signal processing

YANG Dong1,LIAO Guisheng1,ZHU Shengqi1,WANG Kai2
(1.National Key Lab.of Radar Signal Processing,Xidian Univ.,Xi’an 710071,China; 2.Unit 91251,PLA,Qinhuangdao 066102,China)

Matrix Completion(MC)theory can recover the under-sampled data in the array signal processing,further estimating the direction of arrival(DOA)as the fully sampled data does.However,it is required that the data should be under-sampled randomly in different snapshots which satisfy the randomness of MC theory.When some sensors are unsampled or broken in the whole observing time,the previous method would fail.To address this problem,a new processing method is proposed in this paper. The inner relationship among sensors is used,and then we reshape the signal vector in a single snapshort into an equivalent low-rank matrix,which can be recovered effectively by minimizing the nuclear norm. Simulation results validate the effectiveness of the proposed method.Meanwhile,the method can lower the noie power,and improve the performance of the DOA.

array signal processing;matrix completion;low rank matrix;direction of arrival

TN958.92;TN953+.5

A

1001-2400(2014)05-0030-06

2013-05-29< class="emphasis_bold">网络出版时间:

时间:2014-01-12

国家自然科学基金资助项目(61231017);国家973计划资助项目(2010CB731903)

杨 东(1988-),男,西安电子科技大学博士研究生,E-mail:yangdongxd@gmail.com.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.006.html

10.3969/j.issn.1001-2400.2014.05.006