译码转发中继信道下双层延长LDPC码设计

刘 洋,李京娥,李 颖

(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.电信科学研究院无线移动通信国家重点实验室,北京 100083)

译码转发中继信道下双层延长LDPC码设计

刘 洋1,2,李京娥1,2,李 颖1,2

(1.西安电子科技大学综合业务网理论及关键技术国家重点实验室,陕西西安 710071; 2.电信科学研究院无线移动通信国家重点实验室,北京 100083)

译码转发中继系统中双层延长低密度奇偶校验(LDPC)码设计,一般采用双层密度进化算法,固定下层变量节点度分布来搜索上层变量节点度分布,复杂度很高.针对这一问题,提出了高斯近似算法对上下层变量节点度分布进行整体优化,以达到信源到目的和信源到中继两条链路上的传输速率同时最大的目的,复杂度较低.仿真结果表明,文中设计的双层延长LDPC码的译码阈值与理论限的间隔较小,误码性能与利用双层密度进化算法搜索到的最优码集接近.

中继信道;低密度奇偶校验码;高斯近似;整体优化

近些年来,协作通信作为一类通过构造高速率码来获得通信系统协作分集增益的技术越来越受到关注.中继技术是研究最多的协作技术之一.一个经典的三节点中继信道包括一个信源节点(S)、一个中继节点(R)和一个目的节点(D).

译码转发(DF)模式是中继网络中的一种协作技术,Cover和Gamal在文献[1]中证明了DF方案可以达到退化中继信道的容量限.其核心思想是随机装箱技术,即中继译出信源节点的信息,然后将箱子号发送给目的节点,目的节点将接收到的箱子号和在前一个分组接收到的信源信息进行合并处理,译码恢复出源节点的信息.针对单源单中继网络的全双工译码转发模式,Razaghi和Yu在文献[2]中构造了一种双层低密度奇偶校验(Low Density Parity Check,LDPC)码结构.这种编码技术利用结构化的删信或延长设计,能够准确地设计LDPC码,使得同时在信源到中继和信源到目的链路都具有很好的性能.文献[3]将这种双层码结构推广到双源单中继模型,构造了一种网络双层LDPC码,并给出优化设计方法和误码性能.在此基础上,文献[4]提出了一种适用于网络LDPC码的速率兼容算法,可以获得更好的性能.文献[5]进一步推广到多源单中继模型,构造了一种多边类型的网络LDPC码,进行了性能分析和优化设计.

对于双层延长LDPC码的设计,在文献[2]中,作者固定下层码为一个码率容量逼近传输速率R-的传统LDPC码,采用双层密度进化算法搜索上层码的度分布以保证整个码为一个码率容量逼近传输速率R+的延长LDPC码.然而整体的优化算法很难实现,因为需要在置信传播(Belief Propagataion,BP)译码算法的每一歩迭代译码过程中追踪误差概率密度函数,这是一个多维问题.为了简化这个过程,文中提出高斯近似算法,仅追踪消息均值的更新,把消息的概率密度看作一个高斯混合分布[6],来设计用于译码转发中继信道的最优LDPC码,把一个多维问题转化为一个一维问题,使得计算复杂度大大降低.由于缺乏上下层码的整体优化,导致译码阈值和理论限的间隔较大,因此,文中结合高斯近似算法,提出了对信源到目的和信源到中继链路进行整体优化,使得设计的码字性能可以逼近理论限.仿真结果表明,文中设计的码字的译码阈值和理论限的间隔较小,误码性能与利用双层密度进化得到的最优码集性能接近.

1 译码转发

图1所示为高斯退化中继信道模型,X1和X2分别表示信源节点和中继节点发送的编码序列,Y和Y1分别表示目的节点和中继节点接收到的信息序列,则有

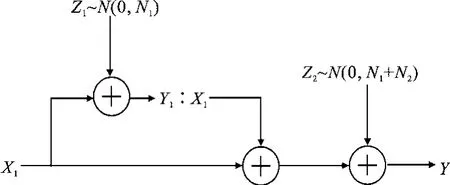
图1 高斯退化中继信道模型

其中,Z1和Z2分别表示中继节点和目的节点的加性高斯白噪声.信源节点和中继节点的功率约束分别为P1和P2.基于Cover和Gamal在文献[1]中提出的译码转发方案,Razaghi和Yu在文献[2]中提出了一种通用的码构造方法可以逼近DF方案的理论限.整个DF转发策略中需要构造两个码字:码率为R2的中继码本X2,在目的节点处能够正确译码,以及码率为R的信源码本X1,需要在中继和目的节点均能够正确译码.在中继节点处,信噪比SNR+=αP1n1;在目的节点处,信噪比SNR-=αP1(N1+N2),且在来自中继节点接收到的额外校验比特(箱子号)的帮助下,才能正确译出X1.二者的码率分别为R+= 0.5 log(1+αP1n1),R-=0.5 log( 1+αP1(N1+N2)),这两个速率也是文中设计的双层延长LDPC码的目标速率.

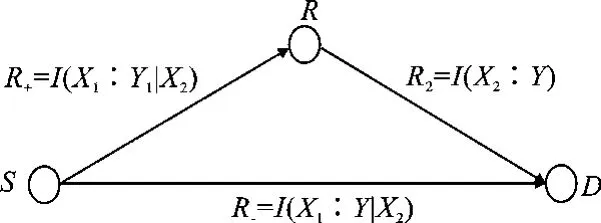
图2 采用DF方案下的可达速率R+,R-,R2

整个系统的译码转发(DF)速率R=min{R+,R2+R-},即

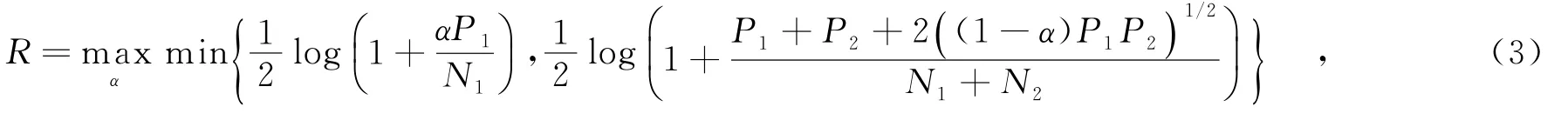
其中,最优比例因子α=1.为了保证目的节点能够成功译码,中继码本X2的速率必须满足

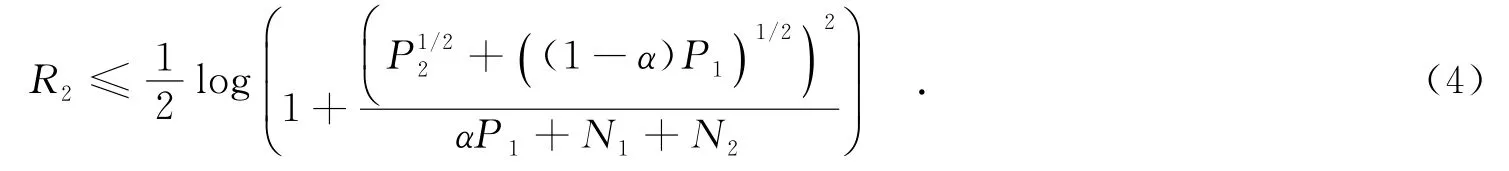
关于DF方案的更多详细内容请参考文献[1].

2 基于高斯近似的双层延长LDPC码的优化设计

2.1 双层延长LDPC码

双层延长LDPC码的Tanner图如图3所示,包含3种类型的节点和两种类型的边.3类节点分别是一类校验节点和两类变量节点即上层和下层变量节点.两种类型的边分别为连接校验节点与上层变量节点的上层边和连接校验节点与下层变量节点的下层边.

双层延长LDPC码的码集由上层变量节点度分布、下层变量节点度分布和两个规则校验节点度dc及d′c定义.下层变量节点度分布λi1,i≥2,表示一条下层边连接到度为i的变量节点的概率.同样地,上层变量节点度分布λi2,i≥2,表示一条上层边连接到度为i的变量节点的概率.下层和上层变量节点度分布和满足和定义参数η为下层边数占总边数的比例,即 η=dc(dc+d′c).

2.2 双层延长LDPC码的优化

文献[2]提出了双层延长LDPC码的密度进化理论,即在每一步迭代中跟踪错误概率的密度函数,这是一个多维问题,复杂度非常高,文中利用高斯近似理论进行简化.

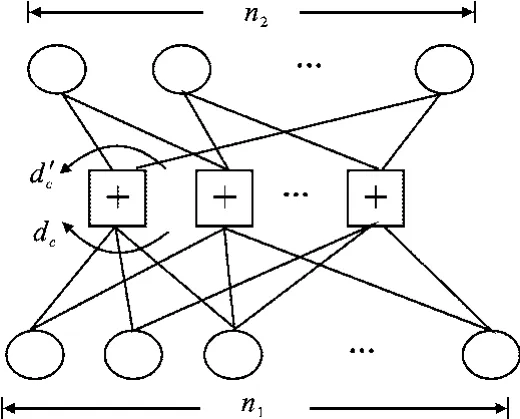
图3 双层延长LDPC码的Tanner图

其中,m0表示信道对数似然信息的均值,且表示信道噪声方差;表示下层图中度为i的变量节点输出的消息均值对应于上层图.

根据和积算法,度为(dc,d′c)的校验节点处的消息更新为

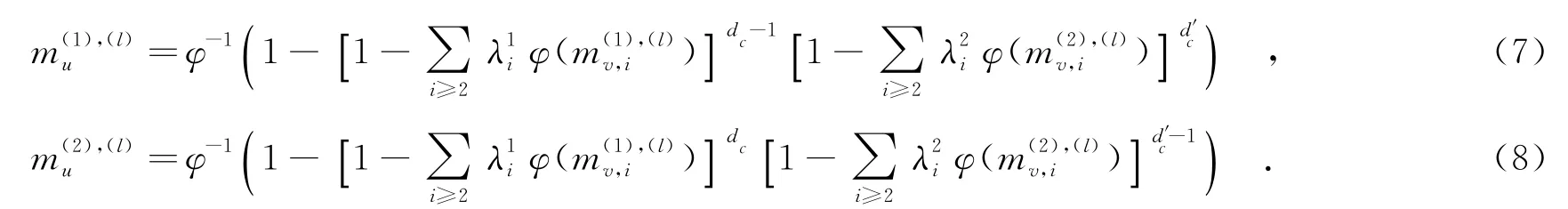
结合变量节点处消息均值的更新,利用式(5)和式(6),可以得到

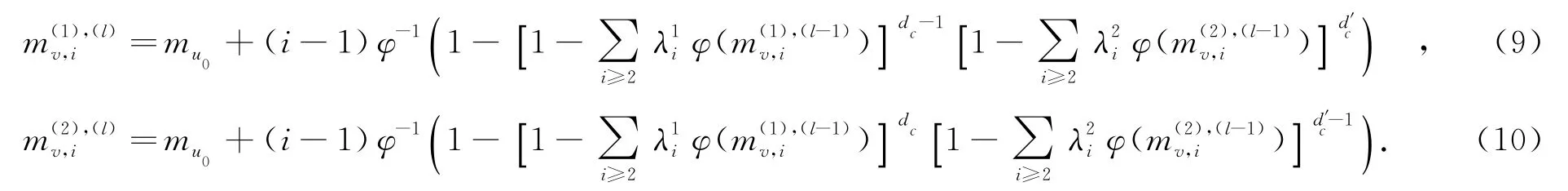
函数φ(x)定义如下:

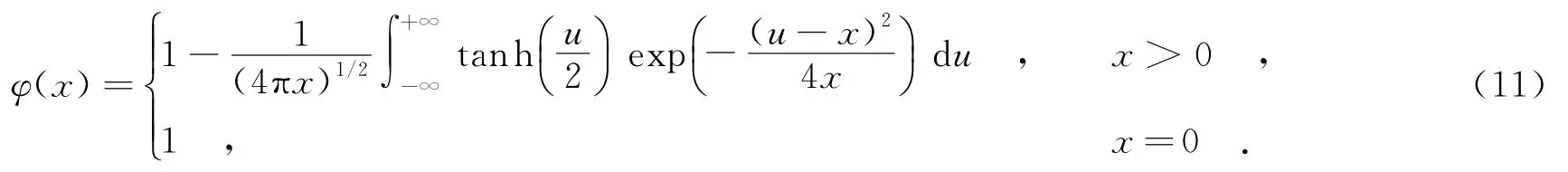
一般,φ(x)可采用文献[3]中的近似形式:

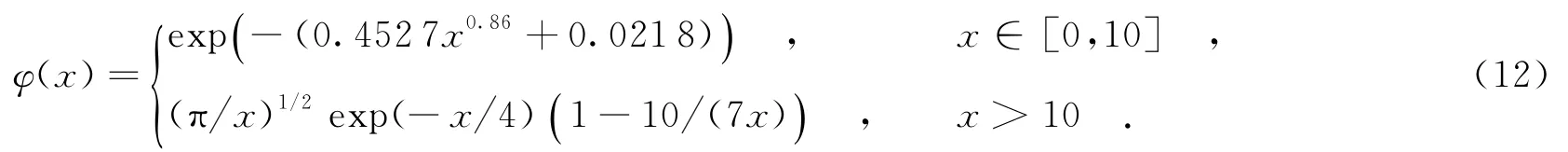
根据式(9)和式(10),可以得到整个变量节点处的平均消息均值更新为

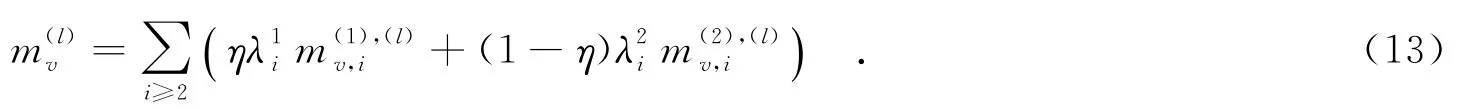
在双层LDPC码中,变量节点的消息均值mv(l)也可以通过上下两层变量节点的平均消息均值按照下层边数所占的比例η和上层边数所占的比例(1-η)进行合成,即

由文献[6]可知,译码成功需满足收敛性条件:

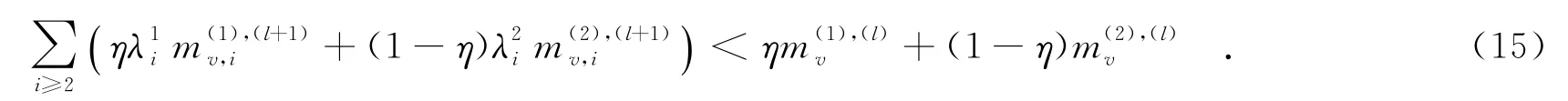
备注:对于LDPC码,针对信源到目的节点的链路,即对应于双层图中的下层图,考虑变量节点度分布为,校验节点的度固定为dc,可以得到

收敛条件为

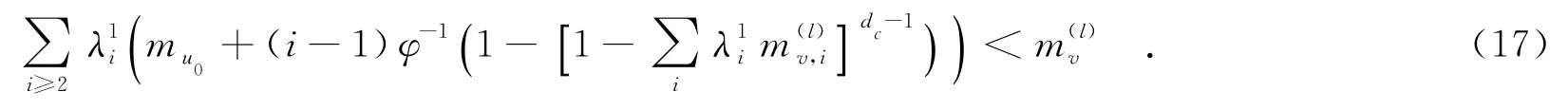
现在考虑整个双层延长LDPC码的优化设计.最优的算法能够同时优化下层变量节点度分布和上层变量节点度分布.文中提出的算法能够最大化下层速率R-,同时可以最大化整体速率R+.双层延长LDPC码的整体码率为1-k(n1+n2),下层码的码率为1-kn1,其中,k表示校验节点的数目,n1表示下层变量节点的数目,n2表示上层变量节点的数目.可以看出,固定n1,n2,dc,d′c,通过最小化k可以达到同时最大化下层速率和整体速率的目的.其中,校验节点数目k和之间的关系

结合约束条件式(15)和式(17),上述问题可以整理为一个线性规划问题:

这里的参数μk,每一次迭代中逐渐增加,最终趋近于1.

表1 (0.5,0.7)双层延长LDPC码码集

表2 (0.3,0.9)双层延长LDPC码码集

3 仿真结果

为方便将仿真结果与文献[2]中的结果进行对比,文中仅考虑AWGN信道,即hSR=hSD=hRD=1,码长N=10 000,采用BPSK调制.针对两组目标码率进行设计:(R-,R+)=(0.5,0.7)和(R-,R+)=(0.3, 0.9),对应的信道分别标记为信道A和信道B,优化得到的码集分别为码集A和码集B,利用文中提出的双层延长LDPC码的高斯近似算法搜索最优码集,分别对比文献[2]中利用双层密度进化算法搜索到的码集F和码集D,结果如表1和表2所示.

对比文献[2]中的结果,针对目标速率(R-,R+)=(0.5,0.7),文中搜索到的码集A和文献[2]中的码集F,译码阈值和理论限的间隔分别为(0.307 9,0.183 6)和(0.346 4,0.247 3),同样地,针对另一组目标速率(R-,R+)=(0.3,0.9),文中搜索到的码集B和文献[2]中的码集D,译码阈值和理论限的间隔分别为(0.515 4,0.246 9)和(0.622 5,0.272 7),由此可以看出,文中设计的双层延长LDPC码的译码阈值与理论限的间隔较小;对比误码性能,可以看出文中搜索到的码集与文献[2]中利用双层密度进化算法搜索到的码集性能接近,同时文中采用的高斯近似算法使得计算复杂度大大降低,误码性能曲线如图4和图5所示.图中垂直实线表示理论限,垂直虚线表示译码阈值,BER为误码率,SNR为信噪比.

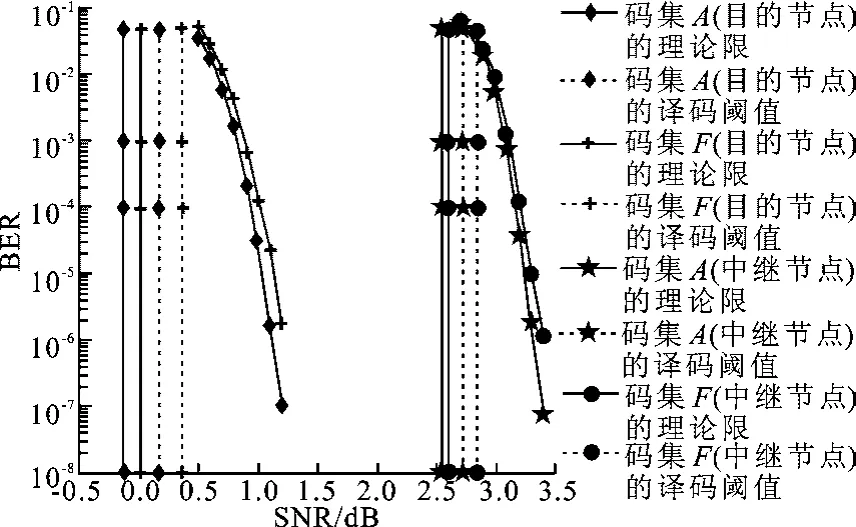
图4 信道A下码集A与参考码集F的性能对比

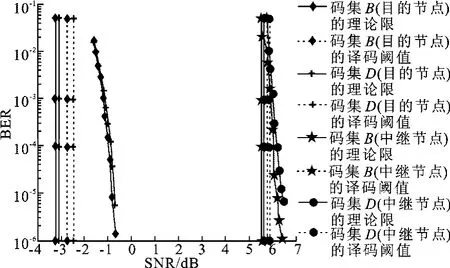
图5 信道B下码集B与参考码集D的性能对比

4 结 论

针对译码转发中继信道,提出了高斯近似算法设计双层延长LDPC码,将双层密度进化算法的多维问题简化为仅利用消息均值的一维问题,复杂度大大降低.同时对码的下层速率和整体速率进行同步优化设计,使得信源到中继和信源到目的两条链路的传输速率同时最大.与文献[2]中的结果相比,通过整体优化搜索到的码集的译码阈值和理论限间隔较小,AWGN信道下的误码性能与文献[2]中利用双层密度进化算法搜索到的最优码集性能接近.

[1]Cover T M,Gamal A A E.Capacity Theorems for the Relay Channel[J].IEEE Transactions on Information Theory, 1979,25(5):572-584.

[2]Razaghi P,Yu Wei.Bilayer Low-density Parity-check Codes for Decode-and-forward in Relay Channels[J].IEEE Transactions on Information Theory,2007,53(10):3723-3739.

[3]Li Y,Song G H,Wang L L.Analysis of the Joint Network LDPC Codes over Orthogonal Multi-access Relay Channel [J].IEEE Communications Letters,2010,14(2):184-186.

[4]王静怡,李颖,孙岳.适用于网络LDPC码的速率兼容算法[J].西安电子科技大学学报,2013,40(2):13-17.

Wang Jingyi,Li Ying,Sun Yue.Rate-compatible Network LDPC Codes[J].Journal of Xidian University,2013,40(2):13-17.

[5]Li J,Yuan J H,Malaney R,et al.Network Coded LDPC Code Design for a Multi-Source Relaying System[J].IEEE Transactions on Communications,2011,10(5):1538-1551.

[6]Chung S Y,Richardson T J,et al.Analysis of Sum-product Decoding of Low-density Parity-check Codes Using a Gaussian Approximation[J].IEEE Transactions on Information Theory,2001,47(2):657-670.

(编辑:李恩科)

Design of bilayer lengthened LDPC codes for decode-and-forward in relay channels

LIU Yang1,2,LI Jing’e1,2,LI Ying1,2
(1.State Key Lab.of Integrated Service Networks,Xidian Univ.,Xi’an 710071,China;2.State Key Lab.of Wireless Mobile Communications,China Academy of Telecommunication Technology,Beijing 100191,China)

The bilayer density evolution algorithm is always used to design bilayer lengthened LDPC codes for the decode-and-forward relay system.The general approach is to fix the lower variable degree distribution and then find an upper variable degree distribution,which has higher complexity.To solve this problem,the Gaussian approximation algorithm is proposed to implement the overall optimization for the lower and upper variable degree distributions.The proposed algorithm aims at maximizing the rates of the source-to-relay and the source-todestination link simultaneously,which has lower complexity.Simulation results show that the gap between the convergence threshold and the theoretical limit of the proposed LDPC codes is smaller and that BER performance is almost the same as that of the ensembles obtained by bilayer density evolution.

relay channel;LDPC codes;Gaussian approximation;global optimization

TN911.22

A

1001-2400(2014)05-0013-05

2013-05-29< class="emphasis_bold">网络出版时间:

时间:2014-01-12

973计划资助项目(2012CB316100);国家自然科学基金资助项目(61072064,61201140,61301177)

刘 洋(1988-),女,西安电子科技大学博士研究生,E-mail:xdyanger@126.com.

http://www.cnki.net/kcms/doi/10.3969/j.issn.1001-2400.2014.05.003.html

10.3969/j.issn.1001-2400.2014.05.003