指向探究的小学数学课堂教学

陈六一

(阳山实验小学校 江苏苏州 215151)

指向探究的小学数学课堂教学

陈六一

(阳山实验小学校 江苏苏州 215151)

当儿童面临某一问题而不能用自己熟悉的方法解决时就会产生认知不平衡，这种不平衡会导致一种“紧张感”，为了消除这种感觉就会产生试图解决问题的动机。如果在问题的诱惑之下，教师以组织者、引导者、合作者的身份适时介入适度指导，逐渐将学习的责任转向学生自己；那么学生通过个性的数学课堂探究，有可能经历深刻的个体思维体验形成探究策略，还有可能在探究中不断生出新的困惑，这样伴随着师生互动的深入，学生会不断丰盈着自己的数学素养。

小学数学教学；课堂探究；学生兴趣；师生互动；观察与猜想；预设与生成

“学生学习应当是一个生动活泼的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式。”[1](P2)如果把课堂教学等同于学生的自主学习，那么课堂40分钟的效率自然大打折扣，因为个人的探究必然是摸着石头过河，曲折艰辛，乃至事倍功半。“学习的过程是每个人根据自己的态度、需要和兴趣，并利用过去的知识与经验，对当前工作的外界刺激(例如教学内容)做出主动的、有选择的信息加工过程。”[2](P12)如果在学生山重水复疑无路的紧张惶惑之际，教师以组织者、引导者、合作者的身份适时介入适度指导，逐渐将学习的责任转向学生自己，那么必然能提高学生数学探究的针对性和有效性。

一、诱人的问题是开展课堂探究的“沸点”

动机是唤起和推动探究行为的原动力，具有指导、监控探究行为的功能；动机能使得探究者只关注有关的诱因，以便使他自己的探究活动能顺利进行。而动机来自于认知的不平衡。当儿童面临某一问题而不能用自己熟悉的方法解决时就会产生认知不平衡，这种不平衡会导致一种“紧张感”，为了消除这种感觉就会产生试图解决问题的动机。

例1-1：教师请学生拿出一副三角尺，请一学生说出一种形状三角尺各角的度数，学生回答：30°，60°，90°；再请另一学生说出不同形状的三角尺三个角的度数，学生回答：45°，45°，90°；教师板书30°+60°+90°=180°，45°+45°+90°=180°，接着教师提出问题：这是否意味着所有的三角形三个内角和都是180°，你能用自己的方法予以证明吗？

随即学生被这一发生在身边自己平时竟没有深入思考的问题所吸引，全身心投入各自的探究之中，有的学生先画出各种三角形，再用量角器量出角的度数，试图算出三角形的内角和；有的学生也先画出各种三角形，再剪下每个三角形的三个角，然后把三个角拼在一起……

可见，当学生的动机被激发之后，才会参与到认知活动中来，智力才会真正地发挥作用。所以，引导学生开展课堂数学探究，就应设计一个诱人的问题，启动学生探究的动机。那么诱人的问题从何而来？笔者的教学经验以为可以从以下四个方面思考：

(一)创设符合学生认知且有趣味的问题

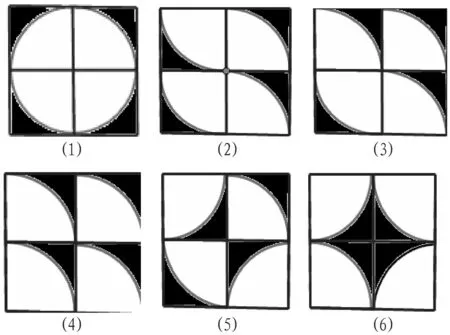
例1-2：组合图形面积问题——教师发给班级每位学生一个正方形和四个半径同为正方形边长一半的“四分之一圆片”，教师请学生用尽圆片，在正方形上建花坛，然后说出每种方案中剩余草坪面积的关系。

对于设计，学生趣味十足，所以探究颇有成效。

教师等学生一一展示了上图方案后，约定6人为一组，合作探究剩余草坪面积的关系，只见有的举例正方形的边长，以具体数字计算，有的用字母代数计算，有的拼剪化归，都得出了结论：尽管图形变化多端，但每种图案中剩余草坪的面积都是相等的，甚至还有学生发现图(2)(3)(4)(5)(6)均可以通过移动，变成图(1)。

(二)从学生的生活现实中寻找问题

佛赖登塔尔认为：“数学的整体结构应该存在于现实之中，只有密切联系实际的数学才能充满着各种联系，学生才能将所学的数学与现实结合。”也就是说，问题的内容应该是学生熟悉的内容，而且现实生活中可能发生。曾经，教师喜欢提出“一个洗澡池，有一个进水管，一个出水管，同时打开进水管和出水管，多少时间可注满水池”之类的问题，这种类型的问题不断被质疑，因为在现实生活中谁有这样放洗澡水的？可见脱离生活现实的数学使人乏味。其实，我们可以把这类问题改造为家庭消费问题。

例1-3：“小亚家决定新购一辆小轿车，如果不动用父母的工资，需要积攒15个月，可事实是父母每个月工资的四分之一都要被消费掉，那么按照这样计算，小亚家靠爸爸妈妈的工资购买这辆小轿车，得需要多长时间？”因为就是学生家庭发生的故事，学生探究的动机就极大地被激发了。

(三)利用学生的作业提出问题

其实，在学生的课内外作业中，教师会经常发现一些共性问题；如果对这些问题不闻不问，错误认知得不到及时修正，甚至有可能被强化，那么不利于学生知识结构化、系统化，在此基础上建立起来的新知识就会如同生活中的“豆腐渣工程”。课堂中教师把这些或典型或共性的错误拿出来，让学生进行探究诊断，因为问题来源于学生自己，探究的动机自然格外强烈。

(四)学生自行提出的问题

学生自行提出问题有两种情况：一是教师提示学生联系情境提出问题，如例1-4；二是学生探究中新产生的疑惑，如例3-1，后面具体阐述。

例1-4[3]：42-27=？教师提示借用回形针来探求这个算式的答案。

学生1：我有42个回形针，用去了27个回形针，我还剩下多少个回形针？

学生2：罗拉有42个回形针，金吉有27个回形针，罗拉比金吉多几个回形针？

学生3：克拉蒂有27个回形针，她需要42个回形针。她还差多少个回形针？

就这三个提问，学生分别开展探究活动。问题情境是学生自己提出的，或者说是同伴提出的，提出问题就意味着探究的“发动机”已经预热。

二、策略的经历是开展课堂探究的“锚点”

“学生是主动探索知识的构建者，而非只是模仿者。”[4](P100)学生的数学建构不是盲人摸象，课堂探究也不是信马由缰、胡乱出击。因此，数学教师应分析数学知识所蕴含的数学活动，并以此为线索，引导学生经历和完成相应的课堂探究。这样，既使学生充分把握数学知识的信息意义，做到知其然也知其所以然，从而积累数学活动经验；又使学生大致经历数学知识的形成过程，以此掌握数学知识所反映的数学思想方法。根据学生的数学现实，帮助学生经历知识数学化和再创造的过程，需要找寻适当的探究策略。

(一)观察与猜想

例2-1：利用计算器计算15×15，25×25，…95×95，并探索规律[1](P88)。学生在计算：15×15=225，25×25=625，35×35=1225，教师可示意学生停止计算，观察结果与乘数的关系，提出自己的猜想。学生一旦观察到了15×15=225=1×2×100+25，25×25=625=2×3×100+25，35×35=1225=3×4×100+25，即可猜想45×45=4×5×100+25=2025，…95×95=9×10×100+25=9025；接着教师引导学生用计算器验证，继而甚至可继续猜想：个位是5的数自己乘自己，可能是5前面的数乘这个数加1的和再乘100，然后加25。其实用计算器依然可以验证这个猜想是正确的。虽然题目是出给小学生探索的，其实等到初中，这个题目就可以螺旋上升到完全平方公式予以证明猜想。

(二)操作与交流

在上文例1-4中，学生1操作后汇报：先摆4链(每链10个)和2个回形针在桌上，把其中1链拆开，形成3链和12个；接着取走2链与7个回形针；最后数一数，还剩1链和5个，即15个回形针。

学生2操作后交流道：(1)摆4链和2个回形针，(2)再摆2链和7个回形针在桌上，(3)为了使42个与27能相互配合计算，42里面要有1链被拆散，(4)拆散42中的1链，回形针成为3链与12个，(5)两组对齐后，各取走7个单独的回形针，(6)两组对齐后，各取走2个单独的回形针链，(7)数一数，罗拉比金吉多了1链加5个。

学生3操作后举手：我的前四步和同学2一样，第五步我是将两组中的链和单个的回形针配对，第六步也是数一数，得到克拉蒂还需要1链加5个或者说单独的15个回形针[3](P207-230)。

以直观分析问题，既呈现探究的过程，又能及时检验探究是否正确。操作中辅以交流，通过语言沟通，逐步实现了数学问题的抽象化。前文“例1-1”的学生探究三角形的内角和的教学，也说明了操作实验这项策略非常适合小学生思维具体性的特点，甚至有四年级的学生做出了如下创造性的操作：

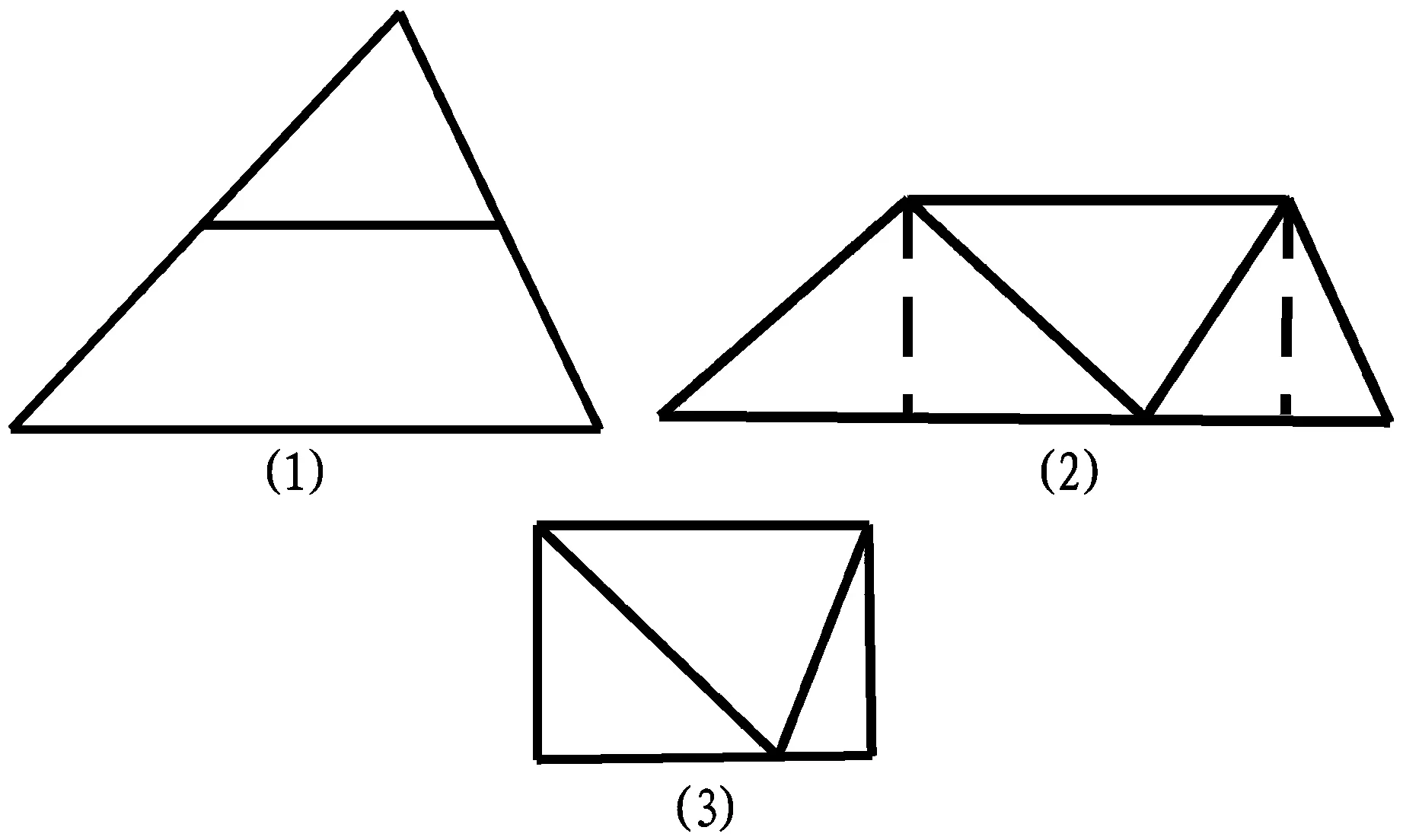
(三)转化与模型

笛卡尔在《更好地指导推理和寻求科学真理的方法论》中给出了一个解决问题的“万能方法”：“第一步，把任何问题都转化为数学问题；第二步，把任何数学问题都转化为代数问题；第三步，把任何代数问题都转化为方程模型予以求解。”可见，当学生在探究数学问题的过程中，借助旧知识、旧经验来处理新的问题，并建立某种数量关系或者变化规律时，也就进入了数学质的学习。如《义务教育数学课程标准2011年版》例34：测量一个土豆的体积。虽然这个挑战能激发学生想到所学正方体、长方体、圆柱、圆锥的求体积模型，但显然又不能直接派上用场。学生自然要探究如何把不规则的土豆转化为规则的正方体、长方体、圆柱或圆锥：最初学生很容易想到通过削切的方式转化，可是这样不能求出土豆准确的体积；于是在失败中有学生尝试把土豆变为土豆泥，再将土豆泥做成规则物体予以求解，貌似合理，可是在课堂里易于实现吗？继之再有学生想到了将土豆转化为一部分水，就有了量杯中盛定量的水，放入土豆，建立“土豆的体积=第一次量杯中水的体积(放入了土豆后的体积)-第二次量杯中水的体积(没有放入土豆的体积)”的模型。

还需要阐明的是，学生通过自己的艰辛探究，收获了某种数量关系，或者发现了某种规律，更能启示学生每一种理论与法则的建立都隐含着数学家们的科学探索精神和科学方法的运用，无论科学知识怎样变化，这种精神和科学方法始终如一，它们才是科学的本质。

三、偶得的生成是开展课堂探究的“动点”

就科学性而言，教学过程要依据一定的教育原理和方法，对整个过程进行预设；就教学的艺术性而言，教学的过程要具有流动性、突变性、差异性和不确定性，许多教学细节是生成的，随机产生的。也就是说：“就人文角度说，人是生成性的存在，生命是不可预测的，儿童的发展具有丰富的可能性，不可限量；就课程角度说，课程不只是文本课程，更是体验课程；就教学角度说，教学不是教师教学生学、教师传授学生接受的过程，而是教与学交往、互动的过程，师生双方相互交流、相互沟通、相互启发、相互补充，在这个过程中，教师与学生分享彼此的思考、经验和知识，交流彼此的情感、体验与观念，丰富教学内容，求得新的发现，教学是一个发展的、增值的、生成的过程。”[2](P84-85)在数学课堂中，师生双方就要捕捉对方的想法，产生积极的互动，以能更加有效地推进学生的探究。

四、结语

学生课堂探究有所得之后，教师应帮助学生做一番梳理。学生的数学课堂探究离不开教师适度、适时、智慧地组织指导；学生进行数学课堂探究，通常在一定动机的诱导下，自主尝试一些经验上的探究策略，并在自主探究的失败与成功中，在与老师和同伴的交流中，或校正或内化或迁移自己的数学知识结构、思维活动经验。从以上教学案例中，还可以得到这样的启示：数学课堂里开展学生探究性学习，并不是有些教师认为的那样随意为之或者中看不中用，它不是传统教学方式的对立面，学生的探究还是以有意义的接受性学习所获得的知识为基础；数学课堂探究性学习的目的也并非要培养更多的数学家，探究的数学知识结果不是课堂所追求的唯一目标；学生开展数学课堂探究重在激发潜藏在学生内心探索、创新的愿望，重在培养学生主动获取数学知识的意识与习惯。

[1]义务教育数学课程标准(2011年版)[S].北京：北京师范大学出版社，2012.

[2]刘家访.上课的变革[M].北京：教育科学出版社，2007.

[3]MarjorieJW.创意教学策略[M]．吕金燮译.中国台北：洪叶文化事业有限公司，1998.

[4]孔企平，张维忠，黄荣金.数学新课程与数学学习[M].北京：高等教育出版社，2003.

(责任编辑：李文玉)

On Mathematics Classroom Teaching with an Exploration of the Subject in Classroom

CHEN Liuyi

(Yangshan Experimental Primary School, Suzhou, Jiangsu, 215151, China)

When children face a problem that they can't solve with their familiar method,there will be a cognitive disequilibrium which will lead to a kind of “tension".In order to eliminate the tension,children have the motivation of solving the problems.In this condition,teachers can lead them to solve these questions by playing the role as an organizer,a guide or a collaborator.Then they can pass the responsibility of study to the students gradually,so that students can explore the world of mathematics with their own thinking.After that,they can find their own study strategies after a profound individual experience of thinking.However,they may have new problems during the thinking.Then,with the deepening of the teacher-student interaction,the students will enrich their knowledge of Mathematics.

mathematics teaching in primary school;classroom inquiry；students' interests;interaction between teachers and students;observation and guess;supposition and generation

2014-03-25

陈六一(1978—)，男，苏州市阳山实验小学校，小学高级教师，奥林匹克数学国家二级教练员。

G623.5

B

1674-6120(2014)10-0100-04