拟序下非连续增算子新的广义不动点定理

姜鑫,薛西锋

(西北大学数学学院,陕西 西安 710127)

拟序下非连续增算子新的广义不动点定理

姜鑫,薛西锋

(西北大学数学学院,陕西 西安 710127)

运用序方法研究了拟序空间X中具A=CB型非连续增算子的广义不动点的存在性问题,证明了在拟序空间X中具A=CB型非连续增算子存在最小广义不动点和最大广义不动点.所得结果推广了相关结论.

拟序关系;拟序拓扑空间;增算子;广义不动点

1 引言及预备知识

算子的不动点定理可以广泛的应用于求解微分方程、积分方程和其他类型的方程[1],在经济均衡理论中也有着广泛的应用[2].然而,非线性泛函分析中序集上增算子不动点定理都要求定理中的序集必须为半序集[1,3-4].但是在数学的一些领域中[5-7],特别是在经济均衡理论中的序关系并不满足半序关系中的反对称性[2],这种序关系在文献[5]中被称为拟序关系,而在文献[6]中被称为不完全偏好关系.为方便起见,本文将这种序关系称为拟序关系.文献[6]研究了序列相容的不完全偏好空间(或拟序空间)X中非连续增算子的广义不动点,而本文是在文献[6]的研究基础上,证明了拟序空间X中具A=CB型非连续增算子存在最小广义不动点和最大广义不动点,进而推广了文献[3,6]中的主要结果.

定义 1.1[5]设X为非空集合,若在X中的某些元素对x,y之间可以定义一种二元关系,记为x≼y,具有下列性质:

(i)对任给x∈X,都有x≼x; (ii)如果x≼y,y≼z,则x≼z,

则称≼为拟序关系,称X为拟序集.称x≼y为y偏好于x.

显然,半序关系一定是拟序关系,而拟序关系未必是半序关系.

定义 1.2[6]设 X 是拟序集,若 x≼y与 y≼ x同时成立,则称 x无差别于 y,记作x～y;若x≼y,且x≁y,则称y严格偏好于x,记作x≺y,其中“≁”表示非无差别关系;设M⊂X,若对任给x,y∈M,关系x≼y与y≼x至少有一个成立,则称M 为X中的全拟序子集.

定义 1.3[6]设X为拟序集,且为Hausdor ff空间,若对X中任意两个序列{xn}和{yn},只要xn≼yn(n=1,2,···),xn→x∗,yn→y∗,就有x∗≼y∗,则称X是序列相容的拟序拓扑空间.

定义1.4[6]设X为拟序集,如果对X中的任何全拟序子集M,都存在可数集{xn}⊂M,使得只要x∈M,x/=supM,就有xn0∈{xn},满足x≼xn0,则称X是按拟序伪可分的.

同理给出按半序伪可分的定义.显然,可分集一定是按拟序(或半序)伪可分的.

定义1.5[6]设X为拟序集,D⊂X,A:D→D为一个算子,若存在x∈D,使Ax～x,则称x为A的广义不动点.

显然,在半序意义下的不动点与广义不动点是等价的.

2 主要内容

设X是拟序集,Ω是X的非空子集,根据定义1.2容易证明X中的无差别关系“～”满足反身性、对称性和传递性,因而关系“～”是X、也是Ω中的等价关系.

定义 2.1[6]任取若存在使u≼v,则记

由于文献[6]中引理1和引理3的证明中没有用到任何拓扑性质,因此文献[6]中引理1和引理3中X不必为拓扑空间,即如下引理2.1和引理2.2.

引理 2.1[6]由X 中的拟序关系“≼”在商集Ω/～中诱导出的序关系“≤”是一个半序,从而Ω/～在序关系“≤”下是半序集.

引理2.2[6]设r:Ω→Ω/～为自然映射,N是Ω/～中的全序子集,则r−1(N)必是Ω中的全拟序子集.

定理2.1设X是拟序集,D=[u0,v0]是X中的序区间,设 (i)存在序列相容的拟序拓扑空间Y及增算子和增算子,使得A=CB;

(ii)B(D)是按拟序伪可分的;

(iii)B(D)中的单调增序列是相对序列紧的;

(iv)u0≼Au0,Av0≼v0.

则A在D中必有广义不动点.

证明令则由条件(iv)可得u0∈Ω,从而Ω/=∅.由引理2.1知,由X中的拟序关系“≼”在商集Ω/～中诱导出的序关系“≤”是半序关系,从而Ω/～在序关系“≤”下是半序集.设M 是Ω/～中任意给定的全序子集,下证M 在Ω/～中有上界.

因为M 是Ω/～中的全序子集,则由引理2.2可知,r−1(M)是Ω中的全拟序子集,再由是增算子可知,B(r−1(M))⊂B(D)是B(D)中的全拟序子集.再由条件(ii)和定义1.4可得,存在可数集{yn}⊂B(r−1(M)),使对任意y∈B(r−1(M)),有yn1∈{yn},满足y≼yn1.令

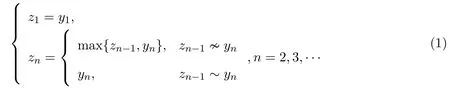
由于B(r−1(M))是全拟序集,故诸{zn}都有定义,{zn}⊂B(r(M)),并且

即{zn}是B(D)中的单调增加序列,由条件(iii)可知,存在{zn}中的子列{znk}⊂{zn}收敛于Y中一点,即存在z∗∈Y,使得

任取n0,当nk≥n0时,有zn0≼znk,再令nk→∞,由定义1.3和条件(i)可知,zn0≼z∗,再由n0的任意性可得,对一切n,都有

由 znk∈B(r−1(M))⊂B(D)可得,Bu0≼znk≼Bv0,再由 (3)式可知,Bu0≼z∗≼Bv0,即 z∗∈B(D).对任意 y∈B(r−1(M)),存在 yn2∈{yn},使得 y≼yn2,又 yn2≼zn2,从而有y≼zn2,再由(4)式可得y≼z∗.因此,z∗是B(r−1(M))在B(D)中的上界,即

令x∗=Cz∗,任给x∈r−1(M)⊂Ω,有Bx∈B(r−1(M)),由(5)式可得Bx≼z∗,由C是增算子可得CBx≼Cz∗,从而Ax≼x∗,再由x∈Ω可得,x≼Ax≼x∗,故

下证x∗∈Ω.由Bu0≼z∗≼Bv0,并利用条件(iv)知,

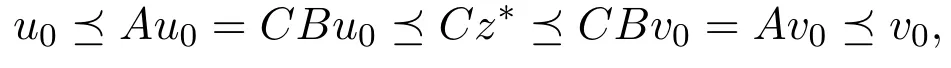
故x∗=Cz∗∈[u0,v0]=D.由(4)式及C的增性知

由于{zn}⊂B(r−1(M)),故可取xn∈r−1(M),使Bxn=zn.注意到xn≼Axn,故由(7)式知再由B的增性即知zn=Bxn≼BCz∗,从而znk=Bxnk≼BCz∗,利用(3)式及条件(i)可得 z∗≼BCz∗.于是由C的增性可知 x∗=Cz∗≼CBCz∗=ACz∗=Ax∗.因此x∗∈Ω,故再由(6)式知,是M 在Ω/～中的上界.根据Zorn引理,Ω/～必有极大元.

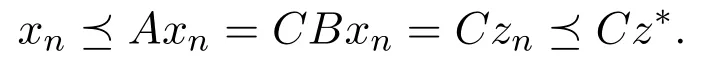
推论 2.1在定理2.1的条件下,若设A满足:

(v)当x,y∈D且x～y时,Ax=Ay,则A在D中必有不动点.

证明由定理 2.1的证明,任取有 y∗～ Ay∗,再由条件 (v)和条件 (iv)可知Ay∗=A(Ay∗),故Ay∗是A在D中的不动点.

推论 2.2设X是序列相容的拟序拓扑空间,D=[u0,v0]是X中的序区间,设

(i)A(D)是按拟序伪可分的;

(ii)A(D)中的单调增序列是相对序列紧的;

(iii)u0≼Au0,Av0≼v0.

则A在D中必有广义不动点.

证明在定理2.1中,令X=Y,A=B,C=I即可.

定理 2.2若定理2.1的条件满足,则A在D中必有最小广义不动点u∗和最大广义不动点v∗,即对任意A的广义不动点x∗,必有u∗≼x∗≼v∗.

证明令

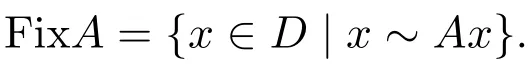
则 FixA/=∅.令 S={[u,v]是X中的序区间 |u,v∈D,u≼Au,Av≼v,FixA⊂[u,v]},显然 D=[u0,v0]∈S,故 S非空.在 S中定义序关系“≤”如下:若 I1,I2∈S且 I1⊂I2,则I1≤I2,则S在序关系“≤”下是半序空间.又I1=I2等价于[u1,v1]⊂[u2,v2]且[u2,v2]⊂[u1,v1],也即 u1≼ u2,v2≼ v1且u2≼ u1,v1≼ v2,即 u1～ u2,v1～ v2,故 I1=I2等价于u1～u2,v1～v2.下证S在半序“≤”下有极小元.

任取S中的全序子集{Iα|α∈Γ}(Γ为指标集),其中Iα=[uα,vα].令R={uα|α∈Γ},显然 R⊂D是 D中的全拟序子集,再由 B的增性可知,B(R)是 B(D)中的全拟序子集.由条件(ii)可知存在{yn}⊂B(R)(n=1,2,···),使对任意y∈B(R),都有yn1∈{yn},使y≼yn1.按照定理2.1同样的方法,可得到{zn}、z∗以及u∗=Cz∗分别满足(1)-(7)式,其中u∗是R在D中的上界,且u∗≼Au∗.下证u∗是FixA的下界.

任取u∈FixA,则u～Au.于是

又由 FixA⊂Iα可知,对任意 Buα∈B(R),有 uα≼u,再由 B的增性可得,Buα≼Bu.

由Buα的任意性可知

再由条件 (i)中 Y的序列相容性和 (3)式可得 z∗≼Bu,再由 C的增性以及 (8)式可得, u∗=Cz∗≼CBu=Au≼u,故

考察P={vα|α∈Γ},同理可证,存在v∗∈D,使得v∗是P在D中的下界,且满足Av∗≼v∗,以及

由(10)式、(11)式,令I=[u∗,v∗],显然I∈S是{Iα|α∈Γ}在S中的一个下界,故由Zorn引理可知,S必有极小元.

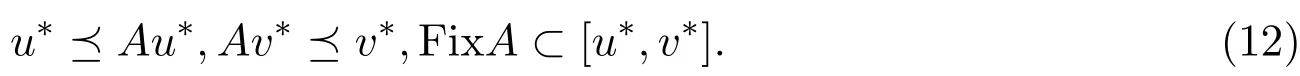
设I∗=[u∗,v∗]是S的极小元,下证u∗～Au∗,Av∗～v∗.由S的定义知,假设u∗≁Au∗,Av∗≁v∗,则由(12)式知u∗≺Au∗,Av∗≺v∗,再由A的增性可得,

对任意x∈FixA,有u∗≼x,x≼v∗,且x～Ax,再由A的增性可得,

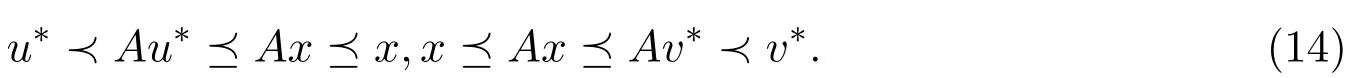
即FixA⊂[Au∗,Av∗],再由S的定义和(13)(14)式知,[Au∗,Av∗]∈S.由(14)式可知这与[u∗,v∗]是 S的极小元矛盾.故 u∗～Au∗,Av∗～v∗,即u∗和 v∗是 A在D 中的广义不动点.再由(12)式可知u∗和v∗分别是 A在D中的最小广义不动点和最大广义不动点.故A在D中存在最小广义不动点和最大广义不动点.

推论 2.3在定理2.2和推论2.1的条件下,A在D中必有最小不动点和最大不动点.

证明在定理 2.2证明中,u∗～ Au∗,Av∗～ v∗,则由条件 (v)可知,Au∗=A(Au∗), A(Av∗)=Av∗,再由FixA⊂[u∗,v∗]=[Au∗,Av∗]可得,Au∗,Av∗即为A在D中的最小不动点和最大不动点.

注 2.1在定理2.1、定理2.2和推论2.1、推论2.3中,A表示为A=CB的形式,其中B映D入另一个拟序拓扑空间Y,而在Y中增序列关于某种拓扑的相对紧性很容易检验.这样,我们把在X中不容易检验的条件转移到容易检验该条件的Y中,从而扩大定理的适用范围.因此定理2.1、定理2.2和推论2.1、推论2.3是文献[6]中定理1、定理2和推论1、推论2的改进.

推论 2.4在推论2.2的条件下,A在D中必有最小广义不动点和最大广义不动点.

证明在定理2中,令X=Y,A=B,C=I即可.

注 2.2定理 2.1、推论 2.2和定理 2.2、推论 2.4是对文献 [3]中定理 1、推论 1和定理2、推论2的改进,主要体现在以下三个方面:

(i)放宽了文献[3]中对序关系的限制,只要求X是拟序集;

(ii)削弱了文献[3]中的紧性条件,例如,由文献[3]中的拟紧性条件可推出本文中的紧性条件,反之则不然;

(iii)进一步放宽了对可分性条件的要求,例如,由文献[3]中的拟可分性可推出伪可分性,反之则不然.

[1] 孙经先.非线性泛函分析[M].北京:科学出版社,2007.

[2] 张金清.序方法与均衡分析[M].上海:复旦大学出版社,2003.

[3] 孙经先.非连续的增算子的不动点定理及其对含间断项的非线性方程的应用[J].数学学报,1988,31(1):101-107.

[4] 孙经先.增算子的不动点定理及其对Banach空间含间断项的非线性方程的应用[J].数学学报,1991,34(5):666-674.

[5] Zhang Jinqing.Zorn lemma on quasi-ordering sets and applications[J].Advances In Mathematics,1999,28(1): 89-91.

[6] 张金清.不完全偏好下非连续增算子的不动点与广义不动点定理 [J].信阳师范学院学报:自然科学版, 2005,18(1):22-25.

[7] Gierz G,Hofmann K H,Klaus Keimel,et al.Continuous Lattices and Domains[M].Cambridge:Cambridge University Press,2003.

Some new generalized fi xed point theorems for discontinuous increasing operator under quasi-order

Jiang Xin,Xue Xifeng
(Department of Mathematics,Northwest University,Xi′an 710127,China)

The existence of generalized fi xed points for discontinuous increasing operators which is expressed as the form A=CB with respect to quasi-order X is studied by using the order method.The existence of minimal and maximal generalized fi xed points for discontinuous increasing operators which is expressed as the form A=CB with respect to quasi-order X is proved,and the obtained results improve the related known works.

quasi-order,quasi-ordered topological space,increasing operator,generalized fi xed point

O177.91

A

1008-5513(2014)04-0406-06

10.3969/j.issn.1008-5513.2014.04.010

2014-03-27.

陕西省自然科学专项基金(2012JM1017).

姜鑫(1988-),硕士生,研究方向：非线性泛函分析.

2010 MSC:47H10