一类推广的Virasoro-like李代数
2014-07-24余德民
余德民
(湖南理工学院数学学院,湖南 岳阳414000)
一类推广的Virasoro-like李代数
余德民
(湖南理工学院数学学院,湖南 岳阳414000)
构造了一类无限维李代数,它是Virasoro-like李代数的推广.研究了这类李代数的两类自同构,这两类自同构均关于映射的合成构成自同构群,一类同构于对称群S3,另一类同构于Klein交换群.得到了这类李代数一些特殊的自同态、中心.证明了这类李代数不是半单李代数.
理想;自同构;同态
1 引言
Virasoro-like李代数是上世纪八十年代作为拟多项式环的一阶微分算子代数被引入的,九十年代在理论物理的广义对称性研究中产生了同样的代数结构.设C为复数域,Z为整数加群,文献[1]定义了一类Virasoro-like李代数g4,并研究了Virasoro-like李代数g4的单性,设g4是由L(a1,a2)(∀a1,a2∈Z)张成的复数域C上的线性空间,李运算定义如下:
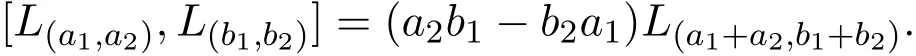
此运算在基向量上线性扩张,并满足反对称性和Jacobi不等式,称g4为Virasoro-like李代数.文献[2]研究了Virasoro-like李代数g4的导子代数和导子代数的自同构群.文献[3]研究了带参数α,β的Virasoro-like的导子代数.文献[4]研究了广义Virasoro-like李代数.作者[5-9]曾研究了Virasoro-like李代数及其推广的Virasoro-like李代数.本文推广了Virasoro-like李代数g4,构造了李代数g,并发现李代数g是一类特殊的李代数,有一些良好的性质.g为C上线性空间,其基向量为:
L(b1,b2,b3,b4,b5,b6,b7,b8)(∀bi∈Z,i∈{1,2,3,4,5,6,7,8}),g=⊕CL(b1,b2,b3,b4,b5,b6,b7,b8).
在g上定义李运算为:

然后,在基上双线性扩张.可验证运算满足反对称性和Jacobi恒等式,从而g为无限维李代数.本文所研究的李代数g实质也是推广的Virasoro李代数.Virasoro李代数及推广的Virasoro李代数的结构和表示一直是李理论研究的热点问题之一.Virasoro李代数及推广的Virasoro李代数的结构和表示与理论物理,量子场论及统计力学等学科有着深刻的内在联系.
本文主要研究了李代数g的理想、自同构、同态.
1 主要结果
构造g中自同构如下:
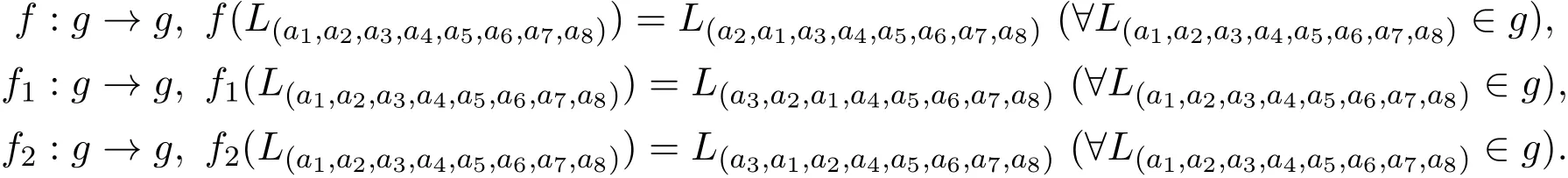
f,f1,f2在 g的基向量 L(a1,a2,a3,a4,a5,a6,a7,a8)上线性扩张.
定理 2.1f,f1,f2是g的自同构.
证明从构造知f为g上的线性映射,且既是单射又是满射.可验证
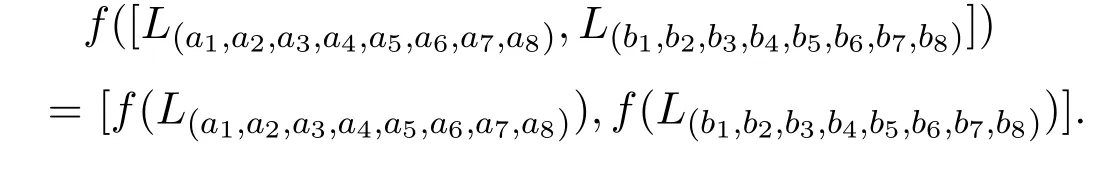
从而(∀x,y∈g)f([x,y])=[f(x),f(y)],同理可证f1,f2是g的自同构.
设g的恒等自同构为e,构造g中自同构如下:

f3,f4分别在 g的基向量 L(a1,a2,a3,a4,a5,a6,a7,a8)上线性扩张.
在映射集H={e,f,f1,f2,f3,f4}中引入映射的普通乘法,即映射的合成“◦”.
∀fi,fj∈H,L(a1,a2,a3,a4,a5,a6,a7,a8)∈g,
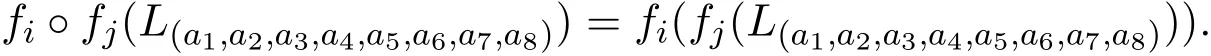
定理 2.2设映射集H={e,f,f1,f2,f3,f4}在上述的乘法运算下,同构于对称群S3.
证明S3的元素分别为(12),(13),(23),(123),(132)和单位元ε,构造映射
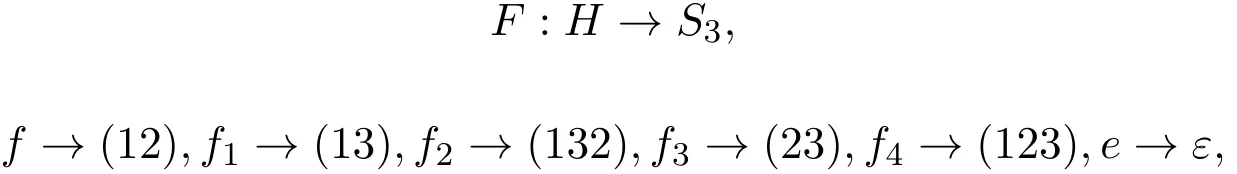
经验证H和对称群S3同构.
构造g中自同构如下:
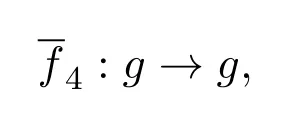
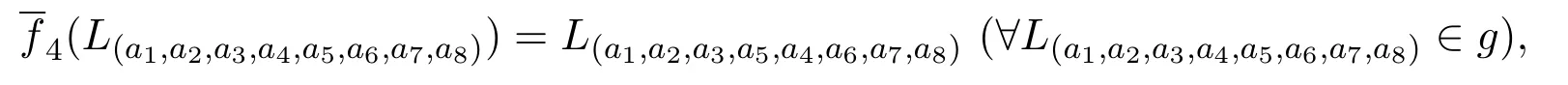
定理2.3关于映射的合成运算构成群.
证明从构造知可为(45),于是→(45),f→(12),f1→(13),f2→(132),f3→(23), f4→(123),→(45),→(12)(45),→(13)(45),→(132)(45),→(23)(45),→(123)(45),则H2构成的群是对称群S5的子群.
(46785)(4)=6,(46785)(6)=7,(46785)(7)=8,(46785)(8)=5,(46785)(5)=4,
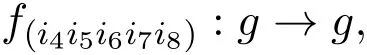
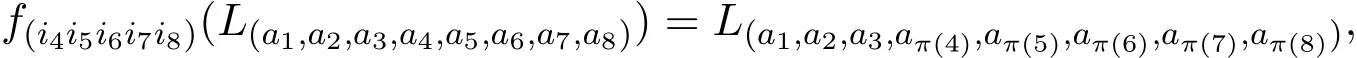
构造g上的自同态映射如下:
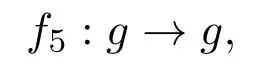
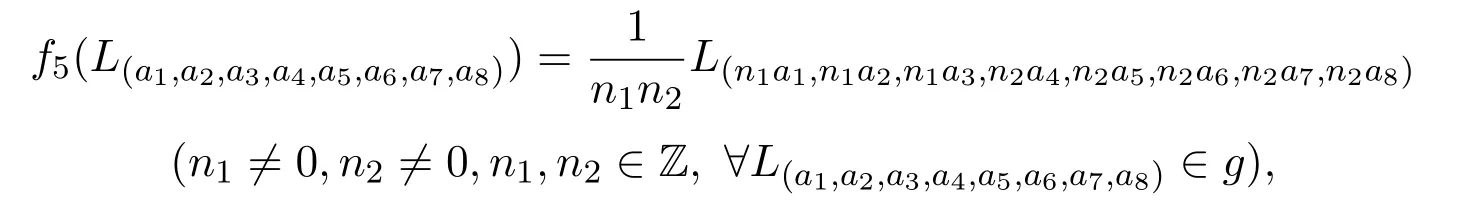
f5在g的基向量L(a1,a2,a3,a4,a5,a6,a7,a8)上线性扩张.
定理2.4f5是g的单自同态.
证明从构造知f5为g上的线性映射,且是单射.∀x,y∈g,f5([x,y])=[f5(x),f5(y)].
在定理(4)中,单自同态f5有如下特殊情形:
当n1=1,n2=1时,f5为恒等同构,记为e;当n1=1,n2=−1时,f5为同构,记为f6;
当n1=−1,n2=1时,f5为同构,记为f7;当n1=−1,n2=−1时,f5为同构,记为f8.
在映射集{e,f6,f7,f8}中引入映射的普通乘法,即映射间的合成.
定理2.5映射集{e,f6,f7,f8}在上述的乘法运算中,构成Klein四元交换群.
证明由于e为单位元,可验证
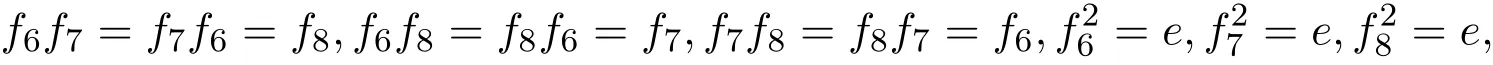
从而定理成立.
定理2.6设g5是所有
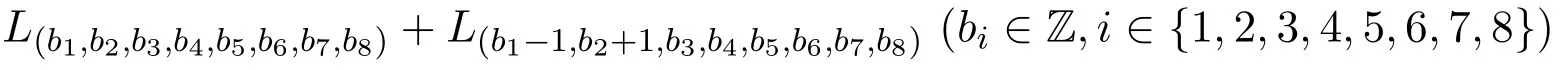
张成的无线微线性空间,即
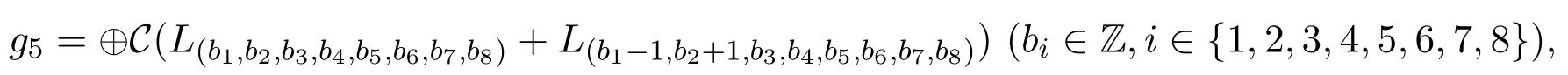
则g5是g的非零真理想,g也不为单李代数.
证明先证g5为理想.因为∀L(a1,a2,a3,a4,a5,a6,a7,a8)∈g,
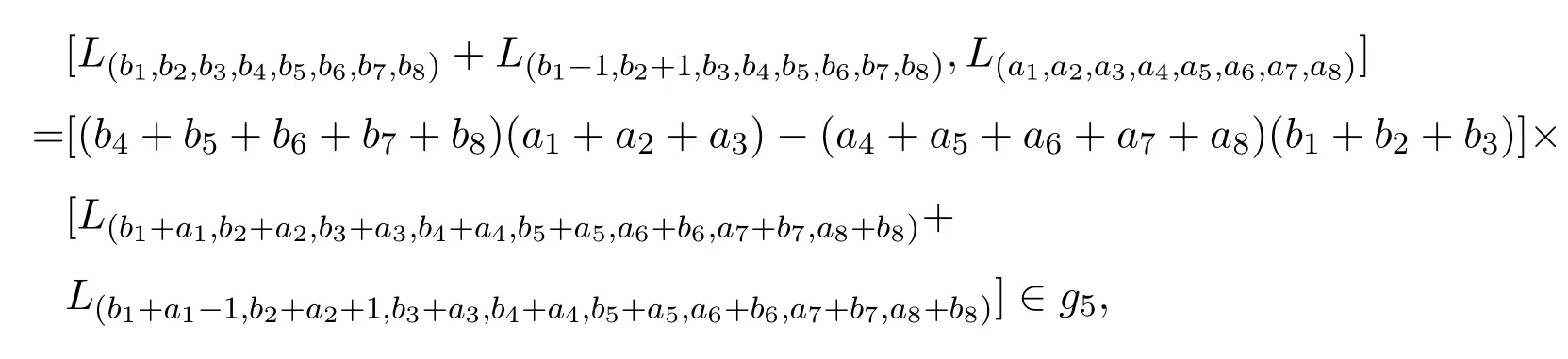
显然g5是真理想.从而定理成立.
定理2.7L(−2,1,1,−1,1,0,0,0)张成的一维子空间是g的一维交换理想,于是g也不为半单李代数.
证明因为∀L(a1,a2,a3,a4,a5,a6,a7,a8)∈g,有[L(−2,1,1,−1,1,0,0,0),L(a1,a2,a3,a4,a5,a6,a7,a8)]=0,从而L(−2,1,1,−1,1,0,0,0)张成的一维子空间是g的一维交换理想,于是g也不为半单李代数.
显然,李代数g的中心C(g)为基向量
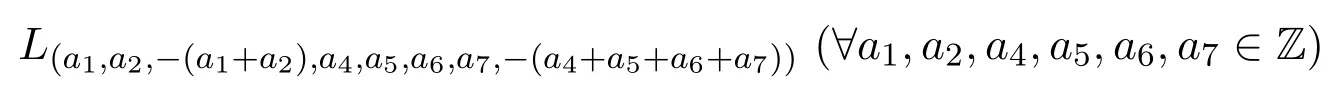
张成的无限维李
子代数.
定理2.8设整数矩阵的秩r(M)<2,则由基向量L(a11,a12,a13,a14,a15,a16,a17,a18),···,L(an1,an2,an3,an4,an5,an6,an7,an8)张成的子空间是g的交换子代数.
证明由于秩r(M)<2,所以r(M)=0或r(M)=1.
当r(M)=0时,矩阵M的每一个行向量都为零.对任意的i,
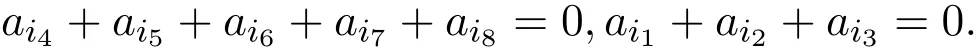
从而由基向量
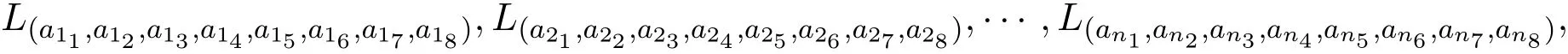
张成的子空间是g的交换子代数.
当r(M)=1时,由r(M)=1知M的任何子矩阵的秩为1或0,即
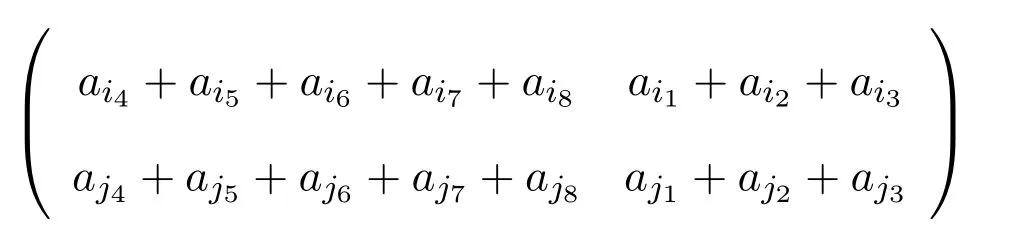
的秩为1或0,无论哪一种情况都有
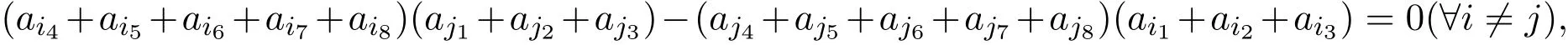
从而定理成立.
在g的基向量中引入字典序,即对

(1)如果k1≺q1,则L(k1,k2,k3,k4,k5,k6,k7,k8)≺L(q1,q2,q3,q4,q5q6,q7,q8),
(2)如果ki=qi,而ki+1≺qi+1,∀i∈{1,2,3,4,5,6,7},则
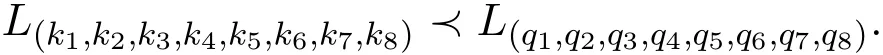
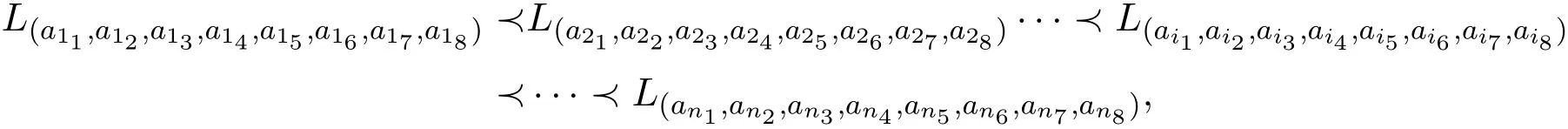
则称x已按字典序排列,L(a11,a12,a13,a14,a15,a16,a17,a18)称为x的极小项,而k1称为x极小项的系数.
设g+是由基向量L(a1,a2,a3,a4,a5,a6,a7,a8)(ai∈Z+(正整数集),∀i∈{1,2,3,4,5,6,7,8})张成的g的线性子空间,显然g+为李子代数.
定理2.9g+中不存在二维非交换子代数.
证明假设g+中存在二维非交换子代数,则g+必存在基x,y使得[x,y]=x.设kiL(ai1,ai2,ai3,ai4,ai5,ai6,ai7,ai8)(∀ki/=0),qjL(bj1,bj2,bj3,bj4,bj5,bj6,bj7,bj8)(∀qj/=0),且x与y已按字典序排列.因为
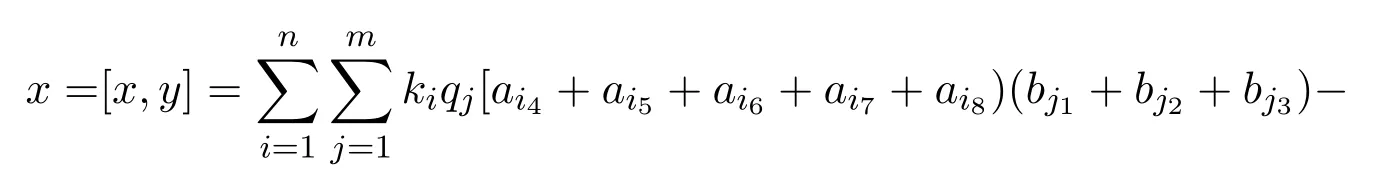
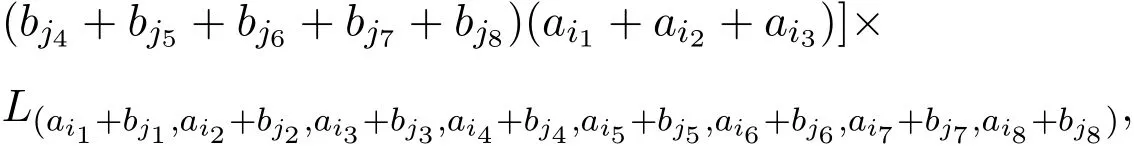
而[x,y]中极小项为L(a11+b11,a12+b12,a13+b13,a14+b14,a15+b15,a16+b16,a17+b17,a18+b18),而x的极小项为L(a11,a12,a13,a14,a15,a16,a17,a18),系数为k1,因为a11,a12,a13,a14,a15,,a16,a17,a18,b11,b12,b13,b14,b15,b16,b17,b18∈Z+,
于是等式x=[x,y]中左边x极小项的系数k1=0,这与k1/=0矛盾.
[1]Zhang Hechun,Zhao Kaiming.Represent of Virasoro Lie algebra and its q-analog[J].Comm.in Alg., 1996,24(14):4361-4372.
[2]姜翠波,孟道骥.Virasoro-相似代数的导子代数[J].数学进展,1998,27(2):175-184.
[3]徐海霞,卢才辉.无限维李代数L(α,β)的导子代数[J].数学学报,1998,41(4):859-864.
[4]Su Yucai,Zhao Kaiming.Generalized Virasoro and super-Virasoro algebras and modules of the intermediate series[J].J.Algebra,2002,252(1):1-19.
[5]余德民,卢才辉.Virasoro李代数的子代数若干结果[J].数学学报,2006,49(3):633-638.
[6]余德民,梅超群.一类无限维半单李代数[J].系统科学与数学,2008,28(9):1101-1108.
[7]余德民,卢才辉.李代数L(Z,f,δ)的特殊性质[J].数学进展,2006,35(6):707-711.
[8]余德民,卢才辉.Virasoro李代数的子代数的同构及生成元[J].系统科学与数学,2008,28(1):24-29.
[9]余德民,梅超群,郭晋云.一些特殊项链李代数的同态[J].数学年刊,2009,30(4):551-562.
A generalized Virasoro-like Lie algebra
Yu Demin
(Department of Mathematics,Hunan Institute of Science and Technology,Yueyang414000,China)
In this paper an in fi nite dimensional Lie algebra is constructed and the in fi nite dimensional Lie algebra is popularized Virasoro-like Lie algebra.Two classes of automorphisms are studied.They are automorphism groups with the compostition of mapping.One is isomorphic to symmetry group S3.The other is isomorphic to Abelian group Klein.We get the center and some special homomorphisms of the in fi nite dimensional Lie algebra.We prove that it is not semi-simple Lie algebra.
ideal,automorphisms,homomorphisms
O152.5
A
1008-5513(2014)04-0341-06
10.3969/j.issn.1008-5513.2014.04.002
2014-04-23.
湖南省教育厅重点项目(12A058);湖南省重点建设学科建设项目.
余德民(1975-),博士,副教授,研究方向:李代数.
2010 MSC:17B05,17B30
