MLinex损失函数下Gamma分布的尺度参数的Bayes估计
2014-07-24金秀岩
金秀岩
(广东松山职业技术学院基础部,广东 韶关 512126)
MLinex损失函数下Gamma分布的尺度参数的Bayes估计
金秀岩
(广东松山职业技术学院基础部,广东 韶关 512126)
在MLinex损失函数下,利用Bayes估计方法研究了Gamma分布的尺度参数的Bayes估计,并证明了其容许性.结果是:在Mlinex损失函数下得到了Gamma分布尺度参数唯一的Bayes估计的一般表达式及其精确表达式,并证明是可容许的.最后通过数值分析实例,说明了所用的参数估计方法是合理可行的.
MLinex损失;Bayes估计;尺度参数;可容许性;Gamma分布
1 引言
在统计决策理论中,参数估计的优劣很大程度上依赖于损失函数形式的选择,文献[1-3]在诸如熵损失函数、Linex损失函数、复合Linex损失函数等损失函数下研究参数估计问题,在不同损失函数下研究Gamma分布的参数估计问题也很有必要.
文献[4]提出了MLinex损失函数,并研究了二次损失函数和MLinex损失函数下Pareto分布的Minimax估计;文献[5]研究了加权平方损失函数和MLinex损失函数下一类分布族参数的Minimax估计;文献[6]研究了MLinex损失下BurrⅫ部件可靠性指标的经验贝叶斯估计;文献[7]研究了对数误差平方损失函数和MLinex损失函数下一类分布族参数的Minimax估计.
关于Gamma分布的参数估计,文献[8]研究了q-对称熵损失函数下Gamma分布的尺度参数的估计,文献[9]研究了广义Gamma分布及Beta分布次序统计量的随机比较,文献[10]研究了含区间数据Gamma分布的参数估计,文献[11]研究了截尾Gamma分布无失效数据的贝叶斯可靠性分析等等.但MLinex损失函数下Gamma分布的尺度参数的Bayes估计尚无研究结果,故本文研究MLinex损失函数下Gamma分布的尺度参数的Bayes估计问题,并证明了Bayes估计δB的容许性.最后通过数值分析实例,说明本文的参数估计方法是合理可行的.
MLinex损失函数形式为:
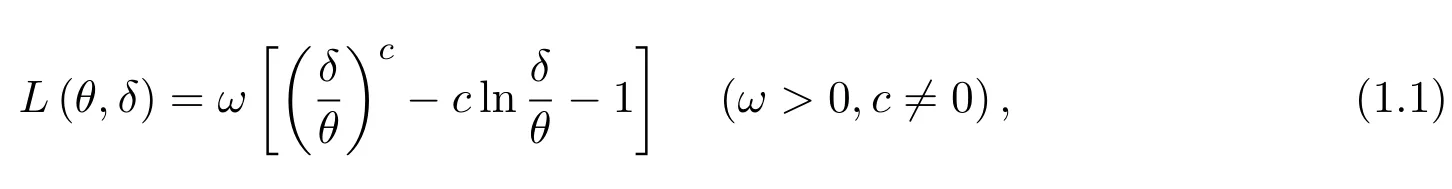
本文仅考虑MLinex损失中c>0的情形,对于c<0情形可类似讨论.
2 尺度参数θ的 Bayes估计
设X1,···,Xn为来自Gamma分布总体X的独立样本,X的密度函数为:
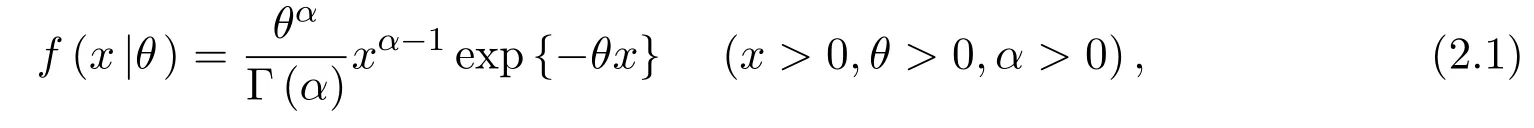
则来自母体的样本X1,···,Xn的联合密度为:

定理 2.1在损失函数 (1.1)和模型 (2.1)下,若在判别空间中存在参数 θ的估计量 δ,其Bayes风险r(δ)<+∞,则对于θ的任何先验分布π(θ),θ的唯一Bayes估计的一般形式为:
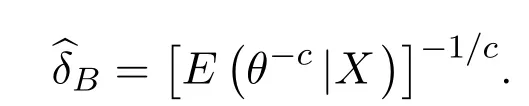
证明在损失函数(1.1)下,δ对应的Bayes风险为:

欲使r(θ,δ)达到最小,只需
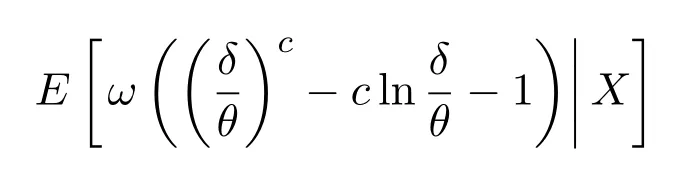
几乎处处达到最小.
由于
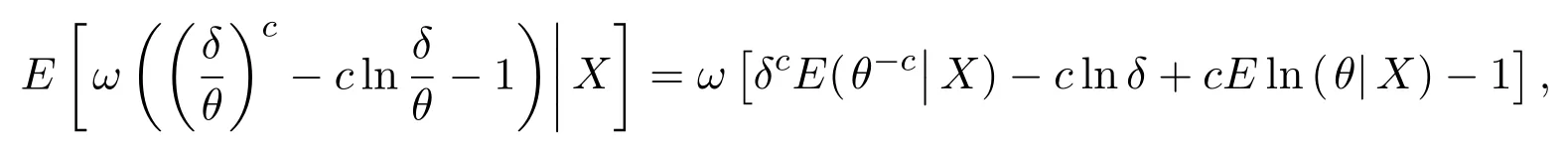
设
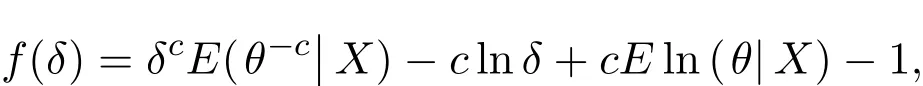
令f(δ)关于δ求导等于零,可解得:
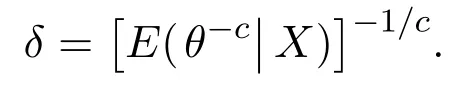
由于f(δ)是凸函数,所以δ是f(δ)的唯一最小值点,故θ的唯一Bayes估计的一般形式为:

定理2.2设x1,···,xn为来自Gamma分布Γ(θ,α)的一个样本观察值,尺度参数θ(形状参数α已知)的先验分布π(θ)取Gamma分布Γ(λ,β),则在损失函数(1.1)下,模型(2.1)的尺度参数θ的Bayes估计的精确表达式为:

证明因为尺度参数θ的先验分布π(θ)服从Gamma分布Γ(λ,β),则θ的密度函数为:
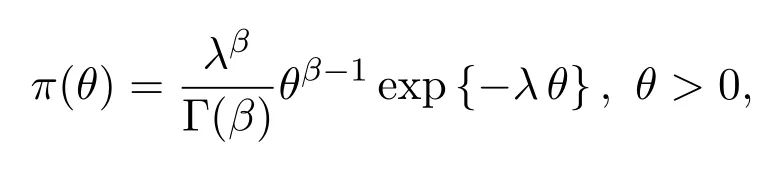
样本似然函数为:
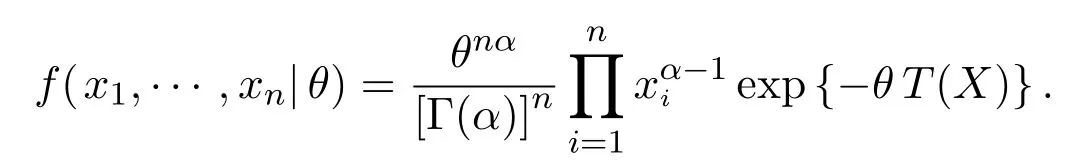
于是,θ的后验分布密度为:
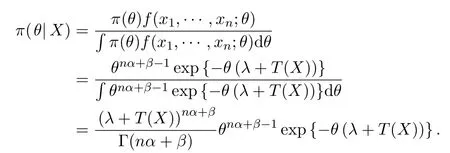
故θ的后验分布密度π(θ|X)服从以λ+T(X)为尺度参数、以nα+β为形状参数的Gamma分布.
由定理2.1以及θ的后验分布密度,有
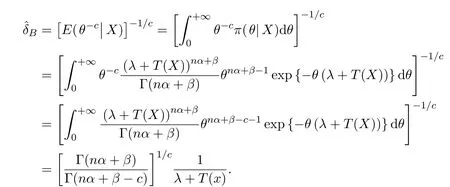
3 Bayes估计的容许性
定理3.1在给定先验分布π(θ)和损失函数(1.1)下,参数θ的Bayes估计ˆδB是可容许的.
证明由于Bayes估计的Bayes风险不大于任何估计的Bayes风险,只须证明存在θ的一个估计δ,其Bayes风险r(δ)<∞,于是可得从而是可容许的.
在(2.2)式中不妨令δ=1,则有
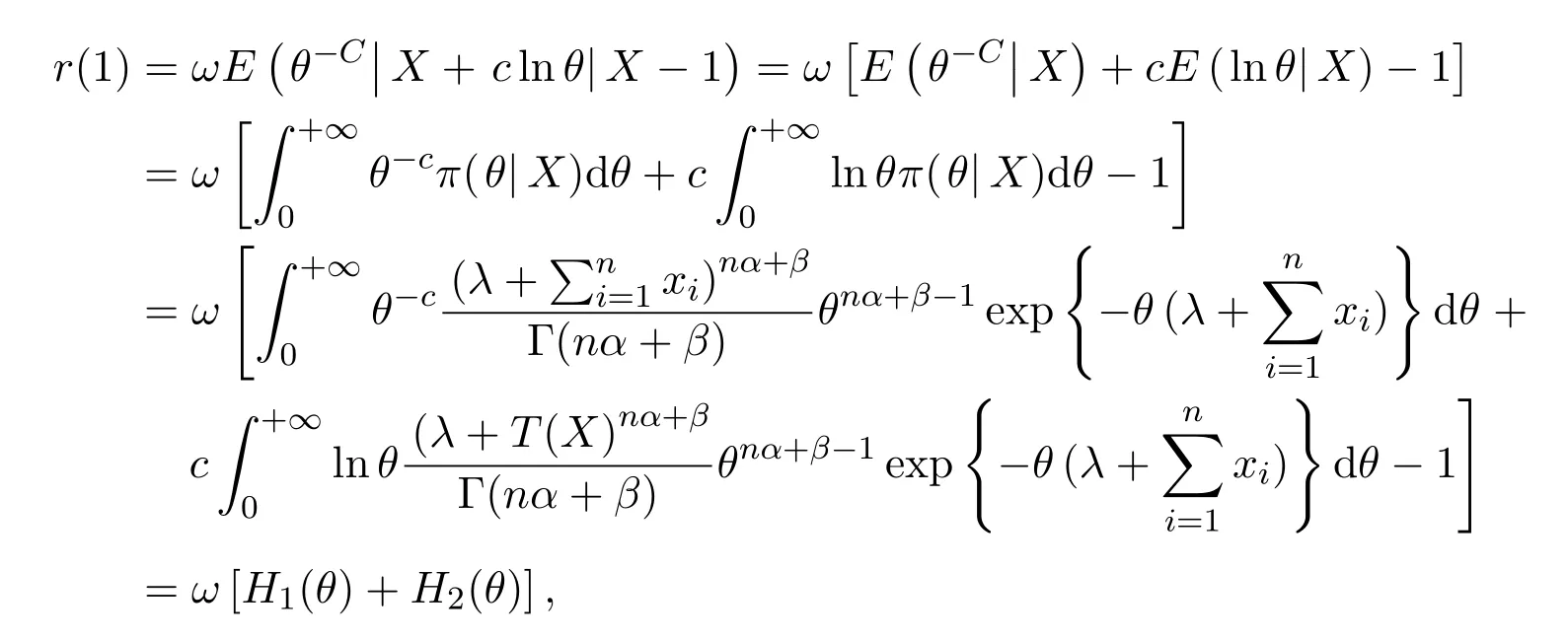
其中,
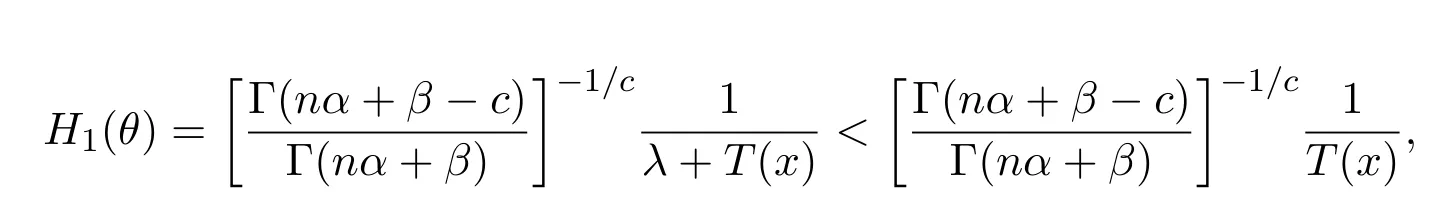
对给定的样本值存在且有界.
而
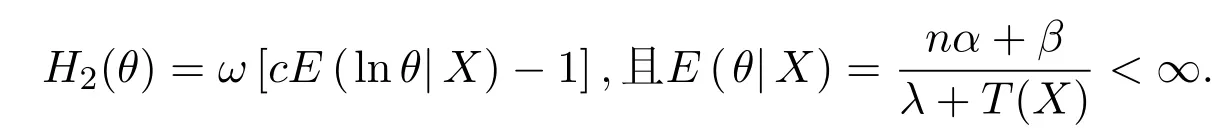
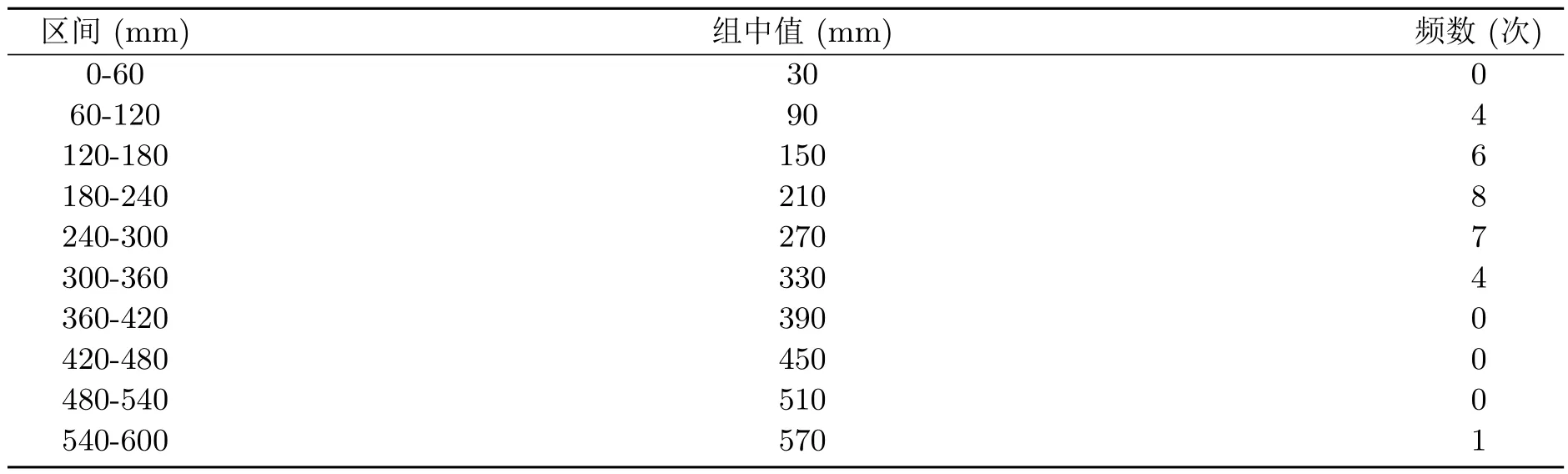
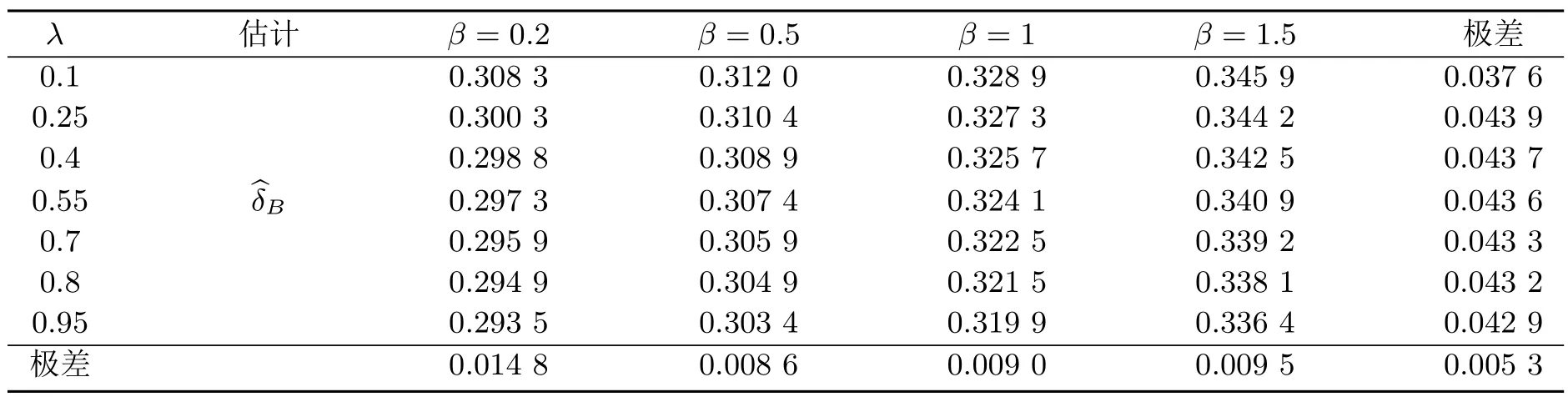
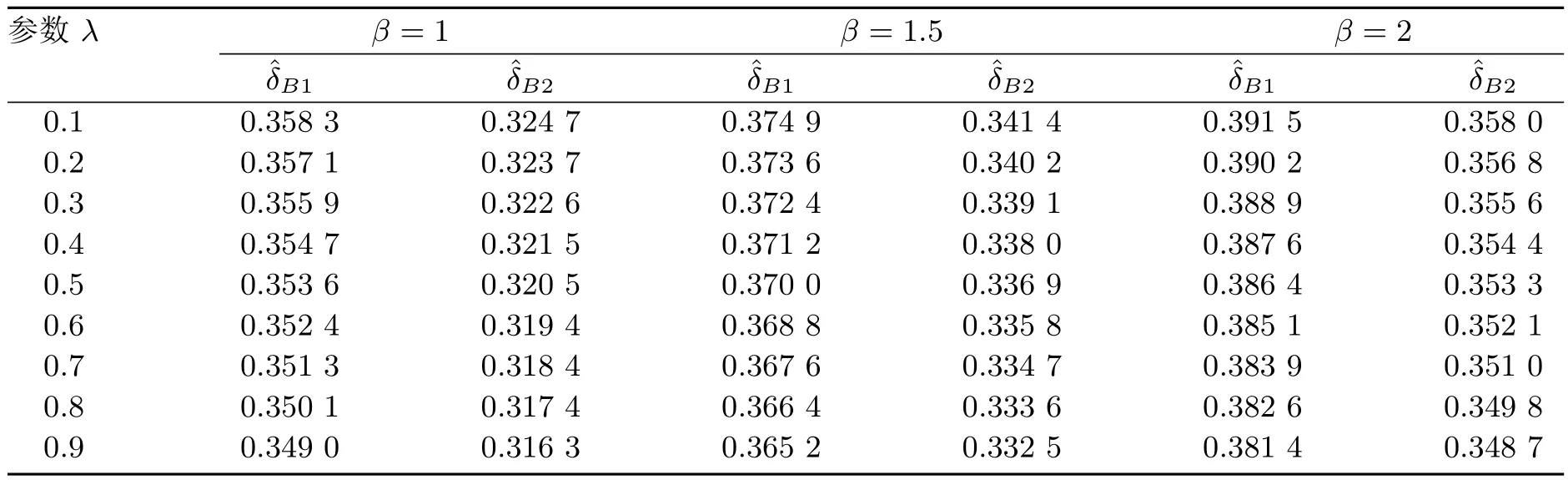
所以,r(δ)存在且有界.又因为r(ˆδB) 4.1 估计量的稳健性与精确性分析 目前,国内外有关气候分析的旱、涝级别划分中,采用一种Gamma分布概率指标来描述降水量所遵从的分布,在这个过程中涉及到一个重要问题就是Gamma分布的参数估计问题.参数估计的好坏程度直接影响到气候分析结果的精确程度,因此Gamma分布的参数估计问题对气候分析显得非常重要.本文以1951−1980年期间北京地区7月份降水量数据为例,取1951−1980年期间降水频数作为求概率密度函数中参数的基本样本[12].具体由表1给出. 表1 该地区6月份降水频数分布 由表 1中数据分析计算可知,该地区 1951−1980年期间 7月份降水频数服从尺度参数θ≈0.326、形状参数为α≈0.978的Gamma分布. 根据这些数据,知T=30,n=10.又根据定理2.2的结果以及文献[8]的研究,为了更具有一般性,根据实际需要选取满足0 表2 尺度参数θ的Bayes估计 则可见其偏差很小,即精确度较高. 4.2 估计量的比较分析 对Gamma分布在复合Linex损失函数、MLinex损失函数下尺度参数θ的Bayes估计结果进行数值比较.为了讨论方便,记Gamma分布在复合Linex损失函数下尺度参数θ的Bayes估计[13]为,在MLinex损失函数下尺度参数θ的Bayes估计(2.3)为,这里依然以上述例子为例,即分别取T=30,n=10的Gamma分布的样本,取c=1.01.比较结果见表3. 表3 Gamma分布在复合Linex损失函数和MLinex损失函数下θ的Bayes估计结果比较 从表 3可以看出,只要根据实际情况合理选择先验分布和 c的取值,Gamma分布在MLinex损失函数下θ的Bayes估计结果相对复合Linex损失函数下的Bayes估计结果来说,效果要好一些,更接近真实值,而且比较稳健. 综合上述分析可知,本文给出的尺度参数θ的Bayes估计是合理可行的. [1] 王德辉,牛晓宁.熵损失函数下巴斯卡分布参数的Bayes估计[J].吉林大学自然科学学报,2001,1:19-22. [2] 杜广富,贺瑞缠.Linex损失函数下位置参数函数的极小极大估计[J].纯粹数学与应用数学,2011,27(3):383-386. [3] 张睿.复合Linex对称损失下的参数估计[D].大连:大连理工大学,2007. [4] Podder C K,Roy M K,Bhniyan K J,et al.Minimax estimation of the parameter of the Pareto distribution for quadratic and Mlinex loss functions[J].Pak.J.Statist,2004,20(1):137-149. [5] 任海平,李中秋.加权平方损失函数和MLinex损失函数下一类分布族参数的Minimax估计[J].统计与决策, 2009,(14):34-36. [6]王琳,师义民,袁修国.Mlinex损失下BurrⅫ部件可靠性指标的经验贝叶斯估计[J].青岛科技大学学报:自然科学版,2011,32(2):34-36. [7] 任海平,阳连武,廖莉.对数误差平方损失函数和Mlinex损失函数下一类分布族参数的Minimax估计[J].江西师范学学报:自然科学版,2009,33(3):326-330. [8] 杜宇静,孙晓祥,万喜昌.q-对称熵损失函数下 Gamma分布的尺度参数的估计 [J].工程数学学报, 2008,25(3):500-504. [9] 叶楠.广义Gamma分布及Beta分布次序统计量的随机比较[D].上海:复旦大学,2006. [10] 蔡全才,徐勤丰.含区间数据Gamma分布的参数估计[J].中国卫生统计,2005,22(2):71-73. [11] 柴永霞.截尾Gamma分布无失效数据的贝叶斯可靠性分析[J].商丘师范学院学报,2011,27(6):5-7. [12] 黄嘉佑.一种用于旱涝分析的降水概率指标—Gamma分布概率指标[J].气象,1990,16(9):8-12. [13] 金秀岩.复合Linex损失函数下Gamma分布的尺度参数的Bayes估计[J].山东师范大学学报:自然科学版, 2013,28(4):65-68. Bayesian estimation on scale parameter of Gamma distribution on the basis of MLinex loss Jin Xiuyan The Bayesian Estimation of Gamma distribution scale parameter has been studied and its admissibility has been proved basing on the MLinex loss function.We obtain two results.First,we get the general expression and exact expression of the Gamma distribution scale parameter under the MLinex loss function,and prove it is admissible.Second,we prove that our method to estimate the parameter are reasonable and feasible. MLinex loss,Bayesian estimation,scale parameter,admissibility,Gamma distribution O212.5 A 1008-5513(2014)04-0347-07 10.3969/j.issn.1008-5513.2014.04.003 2014-03-17. 广东省教育科研“十二五”规划2012年度研究项目(2012JK124). 金秀岩(1961-),副教授,研究方向:数学课程与教学论和概率统计. 2010 MSC:62C124 数值分析实例
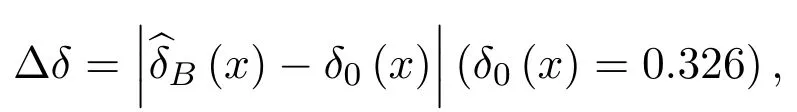
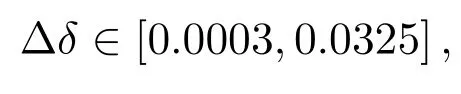
(Department of Basic Courses,Guangdong Songshan Polytechnic College,Shaoguan 512126,China)
