非齐次树上马氏信源的一类Shannon-McMillan定理
2014-07-24金少华卢芳陈秀引王东
金少华,卢芳,陈秀引,王东
(河北工业大学理学院,天津300401)
非齐次树上马氏信源的一类Shannon-McMillan定理
金少华,卢芳,陈秀引,王东
(河北工业大学理学院,天津300401)
通过构造适当的非负鞅,将Doob鞅收敛定理应用于几乎处处收敛的研究,给出了非齐次树上m重非齐次马氏信源的一类Shannon-McMillan定理.
非齐次树;鞅;马氏信源;Shannon-McMillan定理
1 引言
树指标随机过程已成为近年来发展起来的概率论的研究方向之一.强极限定理一直是国际概率论界研究的中心课题之一.文献[1]利用随机变量的截尾方法,给出了H可积下的相依随机变量和的完全收敛定理以及强大数定理.文献[2]利用ND随机变量序列的矩不等式、极大值不等式以及随机变量的截尾方法,研究了ND随机变量序列部分和的大偏差结果和强收敛性.文献[3]研究了两两NQD序列部分和完全收敛性的较一般形式,通过NQD序列的截尾方法以及相关引理,在较宽泛的条件下得到了一类较为广泛的完全收敛性的结果.文献[4]研究了一类随机适应序列部分和的一类新的局部极限定理,得出了一些新结果,并进一步推广了Borel-Cantelli引理.文献[5]利用两两NQD列三级数定理的思想和Chebyshev不等式,研究了两两NQD列在一类广泛条件下的弱大数定理和一类加强条件下的强大数定理,得到了与独立情形一致的结果,还特别讨论了同分布情形,推广了相关文献的结果.文献[6]给出了树指标马氏链的定义并研究了其常返性及角常返性.文献[7]研究了齐次树上某些平稳随机场的熵率.文献[8]定义了在任意状态空间取值的二叉树上的分枝马氏链,并研究了其极限定理.文献[9]给出了Bethe树上非齐次马尔科夫随机场的一类偏差定理.文献[10]首先给出了在可列状态空间取值的二叉树上分枝马氏链定义的离散形式,然后建立了二叉树上分枝马氏链的若干强极限定理,最后研究了二叉树上有限状态分枝马氏链的强大数定理.文献[11]研究给出了非齐次树上二重马尔可夫链的若干强极限定理.本文通过构造适当的非负鞅,将Doob鞅收敛定理应用于几乎处处收敛的研究,给出了非齐次树上m重非齐次马氏信源的一类Shannon-McMillan定理.
2 定义
设T是一个具有根顶点O的无限树,{Nn,n≥1}是一列正整数集,如果第n(n≥0)层上的每个顶点均与第n+1层上的Nn+1个顶点相邻,则称T为广义Bethe树或广义Cayley树.特别地,若对非负整数集N,用模m的同余关系对其分类得到模m的剩余类:
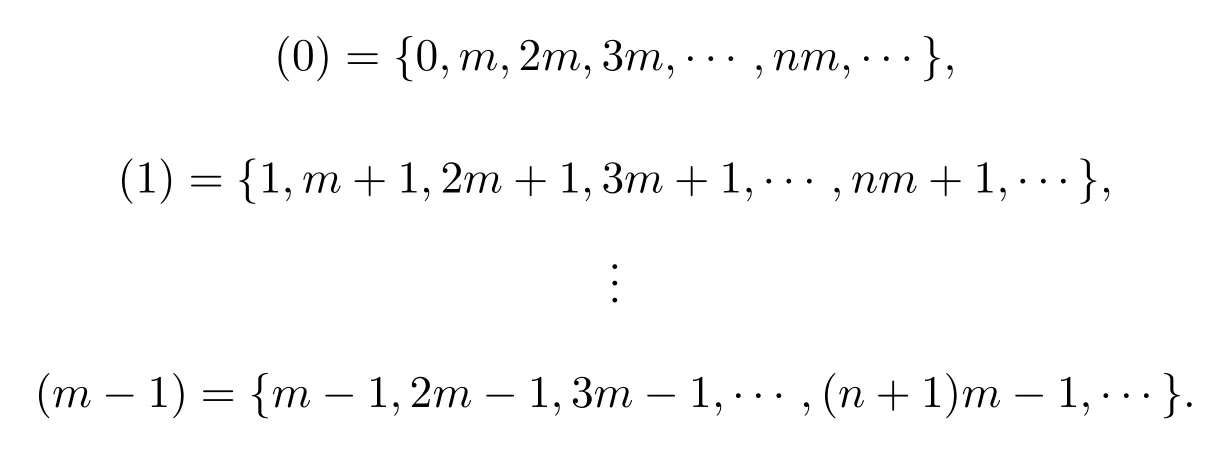
当n∈(i)时,令Nn+1=αi(αi均为正整数且不同时为1,i=0,1,2,···,m−1),就得到了一类特殊的非齐次树Tα0,α1,··,αm−1.
以下恒以T表示树Tα0,α1,··,αm−1,以Ln表示第n(n≥0)层上所有顶点的子图,Tn表示含有从顶点O到第n层上所有顶点的子图.S(t)表示顶点t的所有子代的子图.
定义2.1[12]设(Ω,F,P)为一概率空间,Tn表示树T上含有从o顶点到第n层上所有顶点的子图,|Tn|表示子图Tn的所有顶点数.{Xσ,σ∈T}是定义在该概率空间并于字母集S={s1,s2,···}上取值的任意信源,其联合分布为:

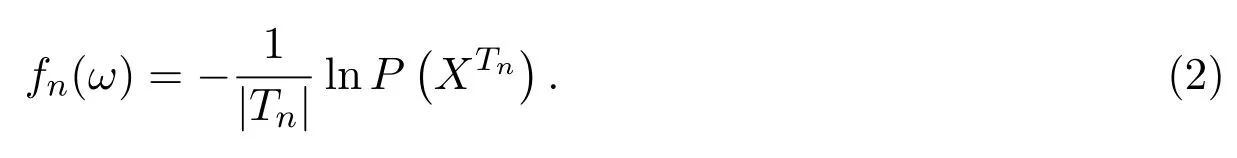
令则称fn(ω)为{Xσ,σ∈T}的相对熵密度.
相对熵密度fn(ω)的极限性质在信息论中称为Shannon-McMillan定理或信源的渐近均分割性,是信息论编码的基础.
定义2.2[13]如果存在STm−1上的分布
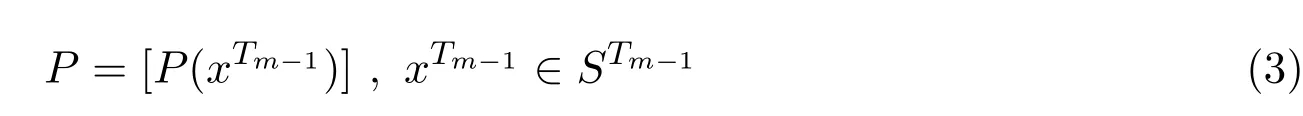
和一列定义在Sm+1上的条件概率组
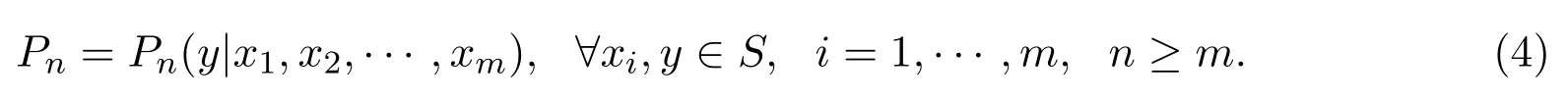
使得∀σ,τ∈T,σ∈Ln,有
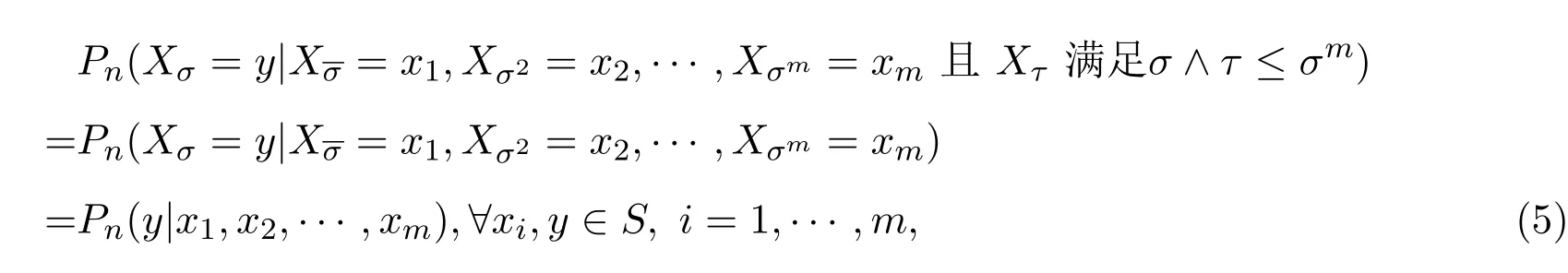
且
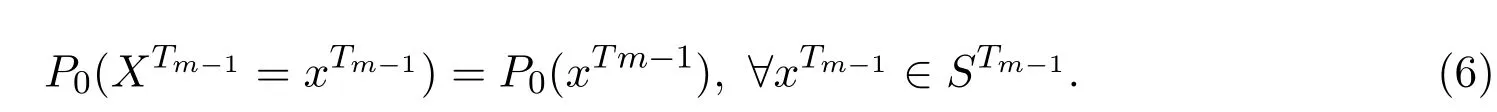
则称{Xσ,σ∈T}为具有初始分布(3)与转移矩阵列(4)的在S上取值的树T上的m重非齐次马尔可夫链.
在上述定义下,树T上的非齐次马尔可夫链的联合分布为:
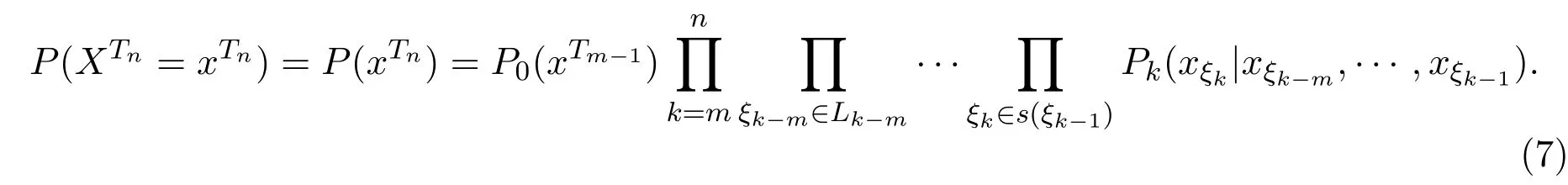
从而有

定义2.3[14]设
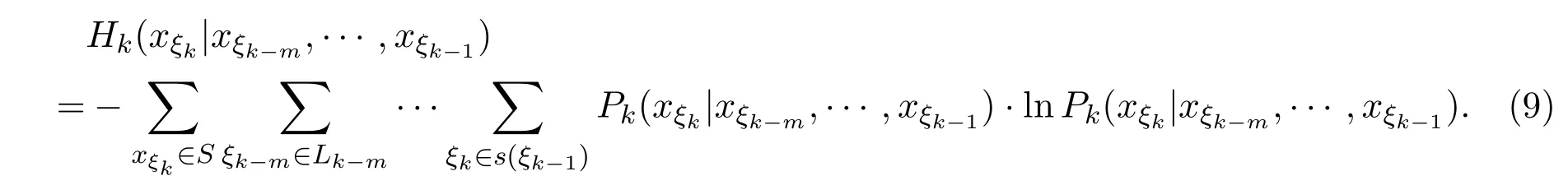
称Hk(Xξk|Xξk−m,···,Xξk−1)为Xξk关于Xξk−m,···,Xξk−1的随机条件熵.
3 主要结果及其证明
引理3.1设{Xσ,σ∈T}为具有初始分布(3)与转移矩阵列(4)的取值于S的树T上的m重非齐次马尔可夫链,λ为一常数,令
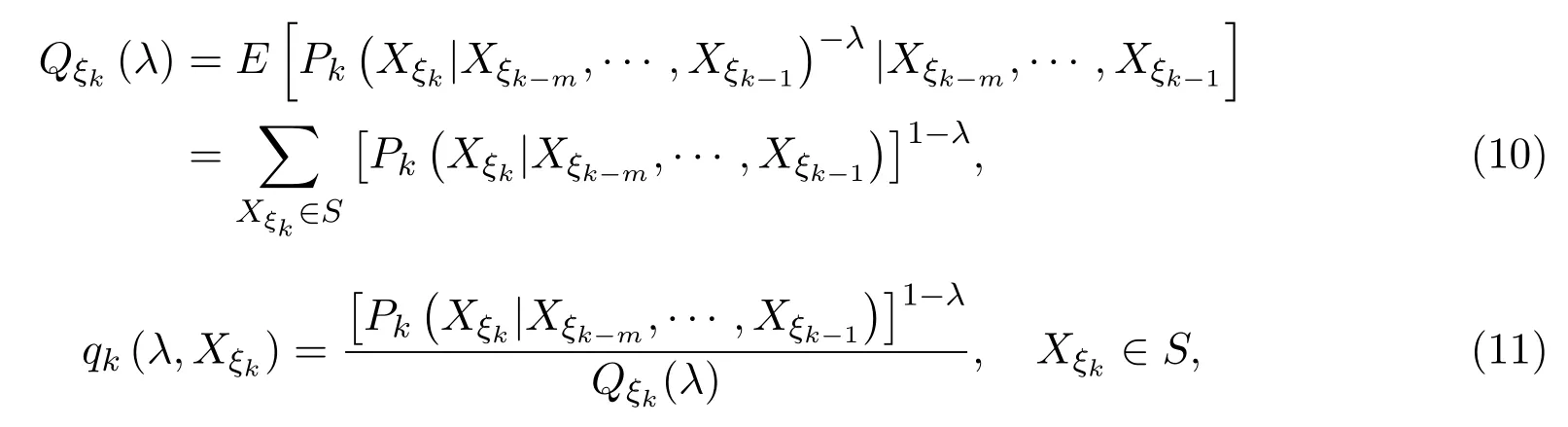
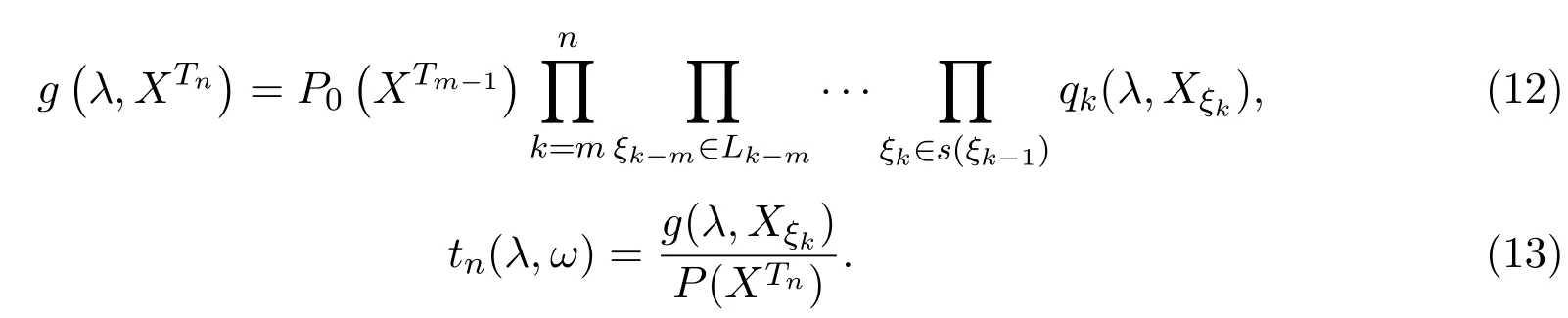
则{tn(λ,ω),σ(XTn),n≥m}是一非负鞅.
证明由于P(XLn=xLn|XTn−1=xTn−1)所以有

而

即
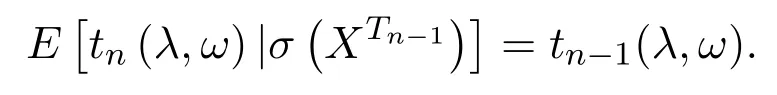
从而{tn(λ,ω),σ(XTn),n≥m}是一非负鞅.
定理3.1设{Xσ,σ∈T}为具有初始分布(3)与转移矩阵列(4)且具有联合分布(7)的非齐次树T上的m重非齐次马氏信源,fn(ω)与Hk(Xξk|Xξk−m,···,Xξk−1)分别由(8)式
和(9)式定义,设α>0,令
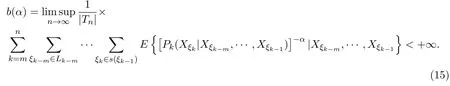
则有
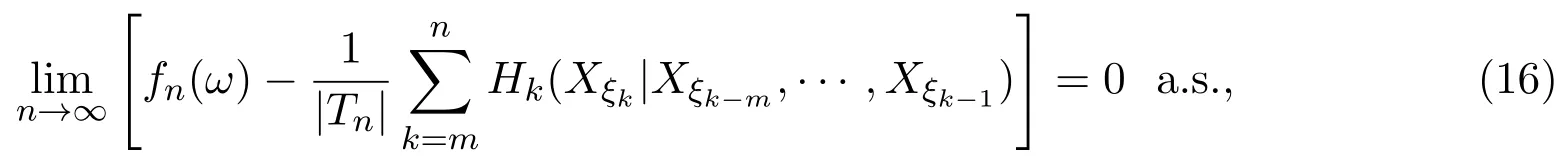
证明取(Ω,F,P)为所考虑的概率空间,由引理3.1知对任意的常数λ,
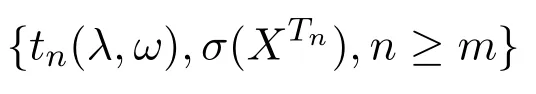
是一非负鞅.故由Doob鞅收敛定理知,存在A(λ)∈F,P(A(λ))=1,使得
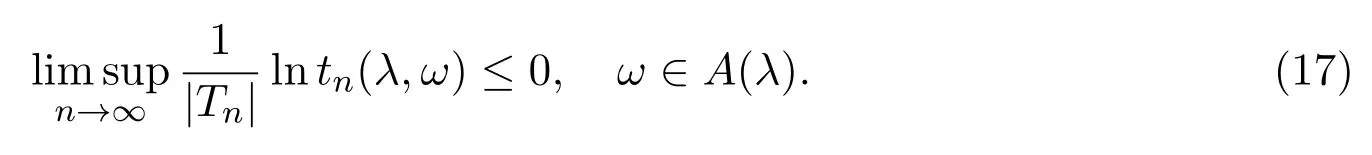
由(13)式与(17)式,有
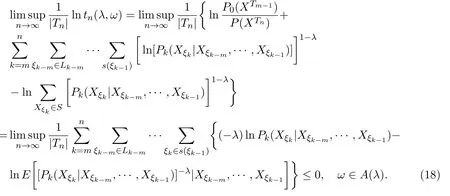
由(18)式,上极限的性质
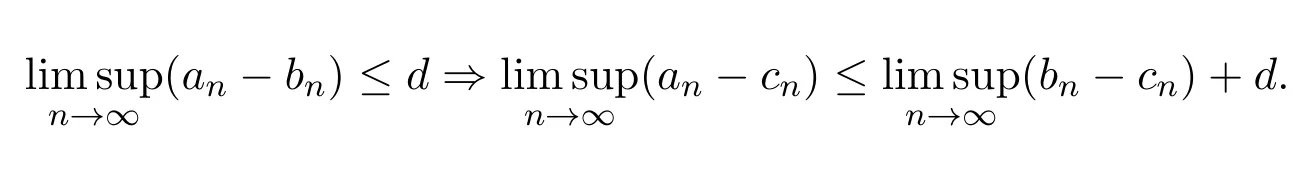
不等式
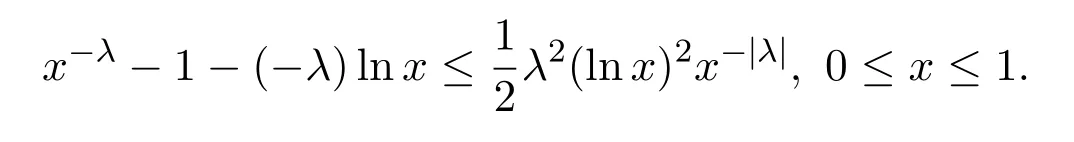
以及不等式
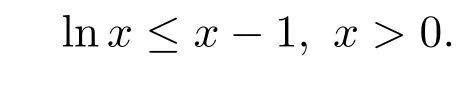
有
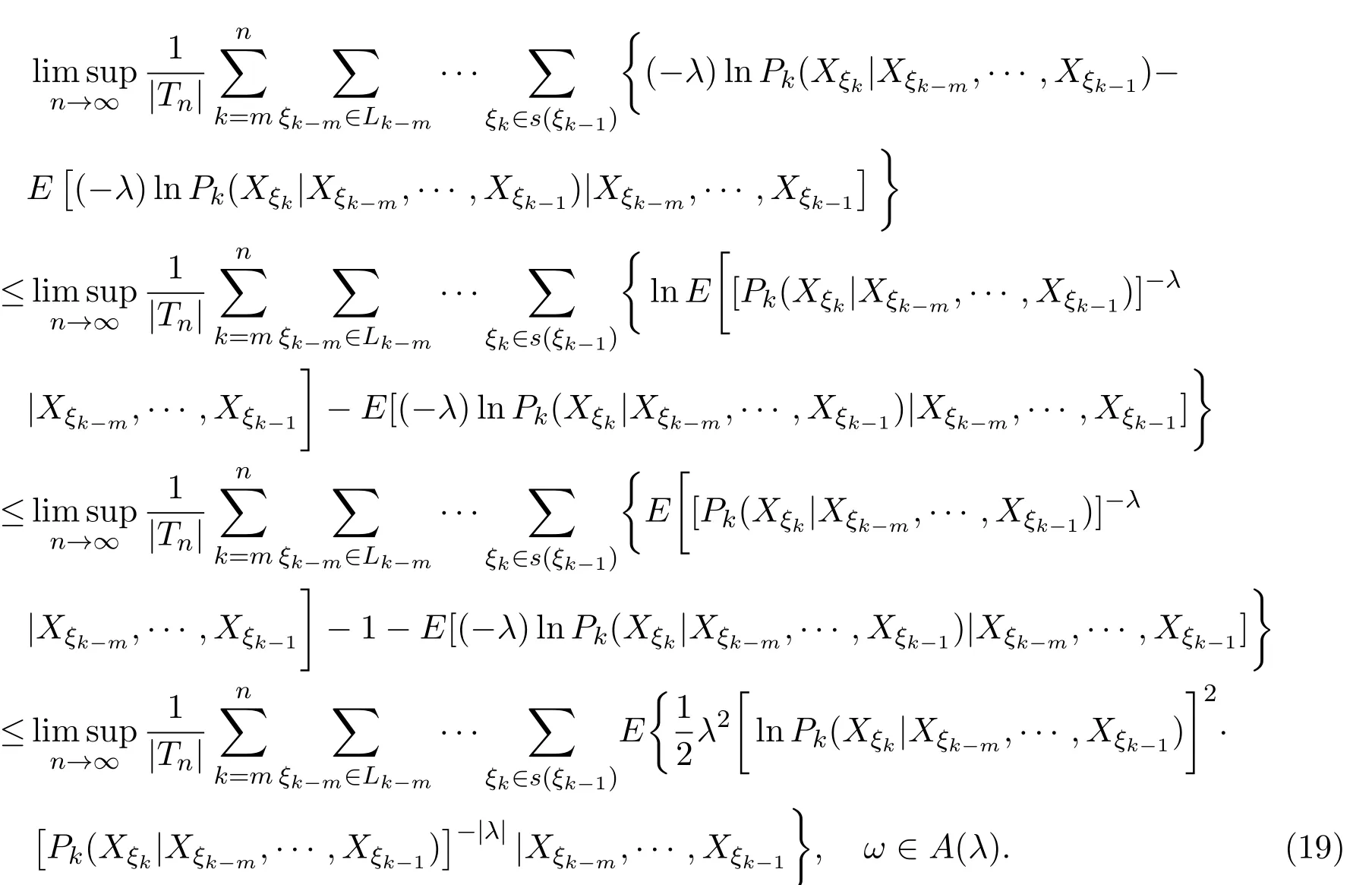
取0 因函数g(x)=(lnx)2xh,h>0,在处达到区间(0,1]上的最大值故有 当0<λ 取0<λi<α(i=1,2···),使得λi→0(i→∞).则对一切正整数i,由(22)式,有 类似地,当−α<−t<λ<0时,将(21)式两边同除以λ,有 与(23)式类似,可证得 由(23)式与(25)式,有 又由(9)式,有 于是由(26)式,有 推论3.1设{Xσ,σ∈T}为具有初始分布(3)与转移矩阵列(4)且具有联合分布(7)的非齐次树T上的m重非齐次马氏信源,fn(ω)与Hk(Xξk|Xξk−m,···,Xξk−1)分别由(8)式和(9)式定义,设α>0,令 则有 证明当0<|λ|<α时,由定理3.1证明中的(19)式,即 当0<λ<α时,将(29)式两端同除以λ,得 取0<λi<α(i=1,2,···),使得λi→0(i→∞).则对一切正整数i,由(30)式,有 类似地,当−α<λ<0时,将(29)式两端同除以λ,得 由(31)式和(32)式,有 由(33)式和(9)式,有(28)式成立. 参考文献 [1] 施明华,周本达,赵建中等.H可积下的相依随机变量和的完全收敛性质[J].纯粹数学与应用数学, 2013,29(4):364-372. [2] 李旭,王学军,刘小涛等.ND序列部分和的大偏差和强收敛性[J].纯粹数学与应用数学,2011,27(6):808-813. [3] 施建华,林影.关于两两NQD序列部分和的完全收敛性[J].纯粹数学与应用数学,2012,28(4):483-492. [4] 薛秀梅,杨卫国.一类随机适应序列部分和的局部极限定理的一个注记[J].纯粹数学与应用数学,2013,29(2):172-178. [5] 王志刚,欧宜贵.两两NQD列大数定律的一个注记[J].纯粹数学与应用数学,2011,27(5):592-599. [6] Benjamini I,Peres Y.Markov chains indexed by trees[J].Ann.Probab.,1994,22:219-243. [7] Berger T,Ye Z.Entropic aspects of random fi elds on trees[J].IEEE Trans.Inform.Theory,1990,36:1006-1018. [8] Guyon J.Limit theorems for bifurcating Markov chains.Application to the detection of cellular aging[J]. Ann.Appl.Probab.,2007,17:1538-1569. [9] Yang W G.A class of deviation theorems for the random fi elds associated with nonhomogeneous Markov chains indexed by a Bethe tree[J].Stochastic Analysis and Applications,2012,30(2):220-237. [10] 党慧,杨卫国,高荣,等.二叉树上分枝马氏链的强大数定理[J].纯粹数学与应用数学,2013,29(5):529-535. [11] 金少华,霍艳,崔春红,等.一类特殊非齐次树上二重马尔可夫链的若干强极限定理[J].数学的实践与认识, 2013,43(2):218-223. [12] 金少华,吕洁.一类非齐次树上非齐次马氏信源的Shannon-McMillan定理[J].河北工业大学学报, 2012,41(2):19-22. [13] 金少华,宛艳萍,陈秀引,等.非齐次树上m阶非齐次马氏链的一类强偏差定理[J].河北工业大学学报, 2013,42(2):61-66. [14] 王康康.任意信源关于赌博系统的一类Shannon-McMillan定理[J].纯粹数学与应用数学,2008,24(2):353-357. A class of Shannon-McMillan theorems for Markov information source on a non-homogeneous tree Jin Shaohua,Lu Fang,Chen Xiuyin,Wang Dong In this paper,by constructing non-negative martingales and appliying Doob′s martingale convergence theorem to the research of a.e.convergence,a class of Shannon-McMillan theorems for m-order non-homogeneous Markov information source on a non-homogeneous tree are given. non-homogeneous tree,martingale,Markov information source,Shannon-McMillan theorem O177.91 A 1008-5513(2014)04-0331-10 10.3969/j.issn.1008-5513.2014.04.001 2014-01-30. 河北省高等学校科学技术研究重点项目(ZD2014051). 金少华(1965-),博士,教授,研究方向:概率极限理论. 2010 MSC:60B12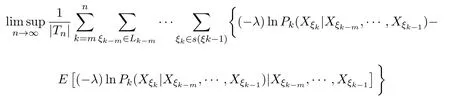
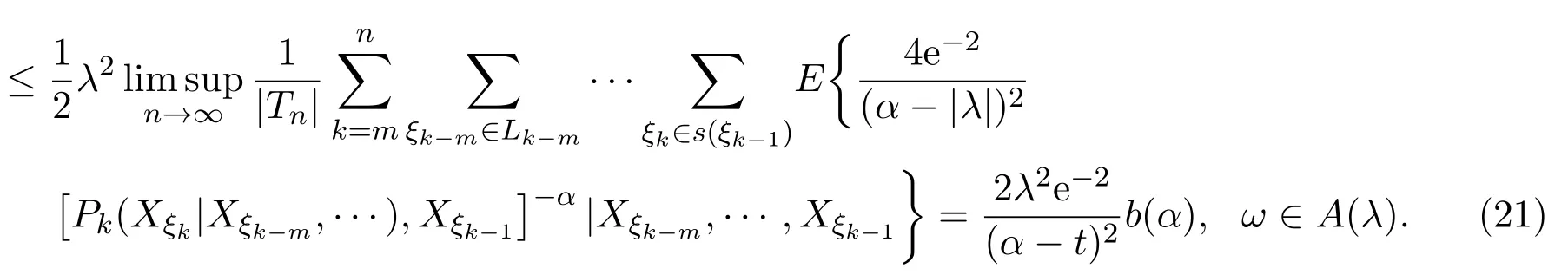
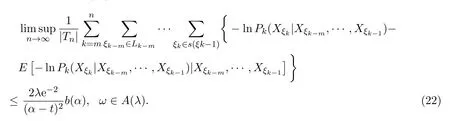
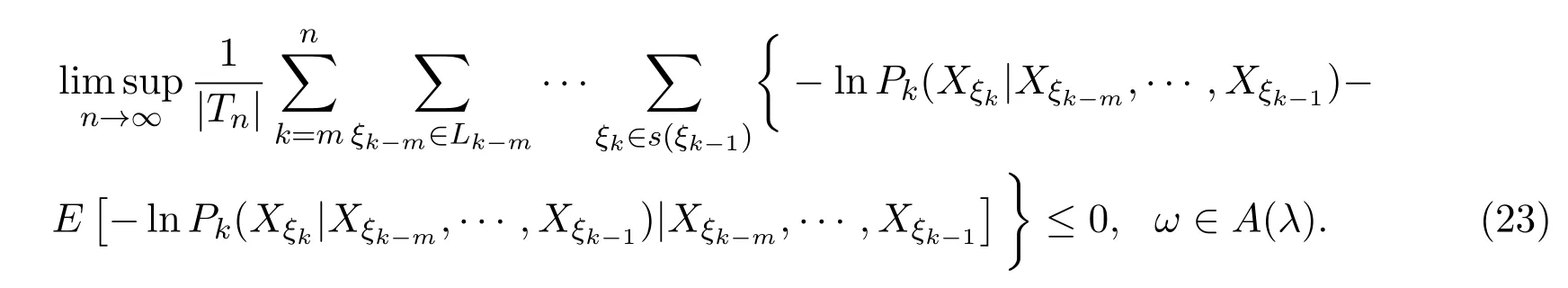
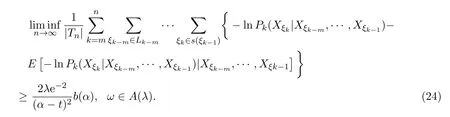

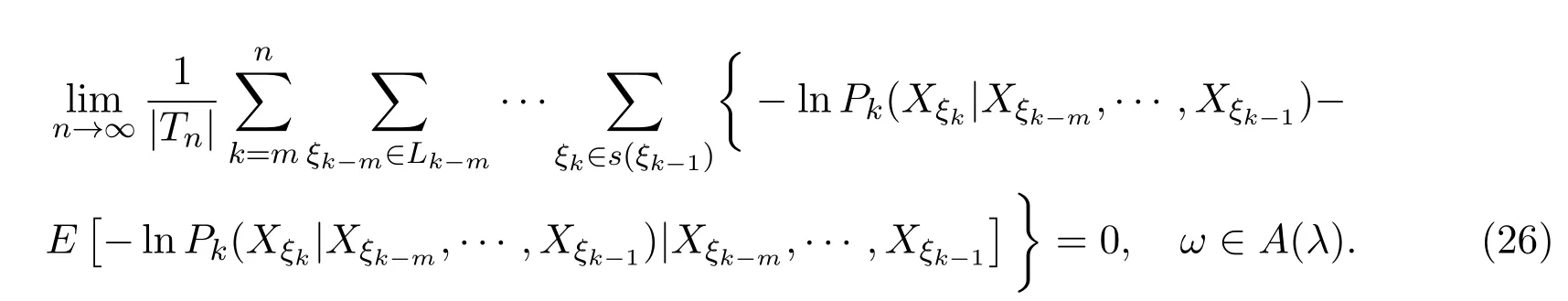
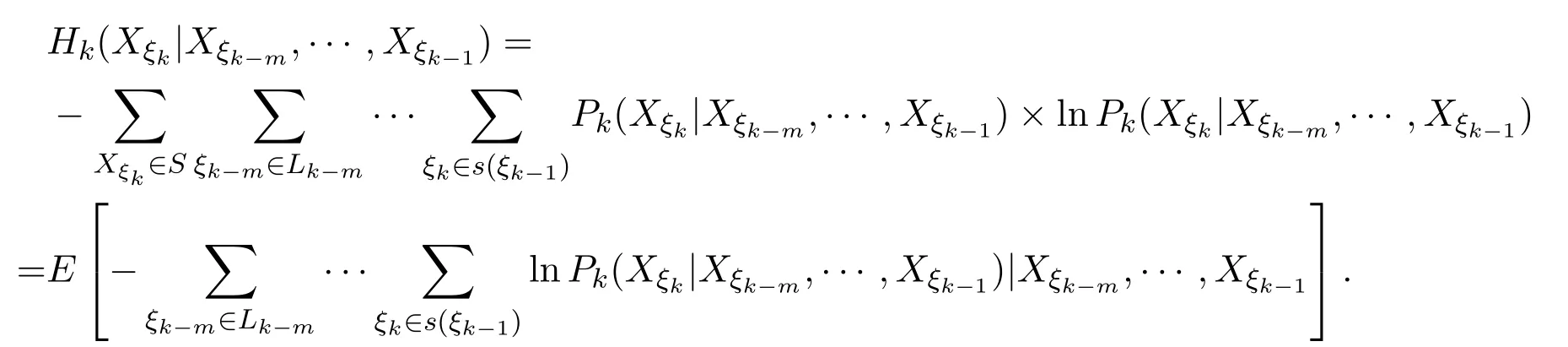
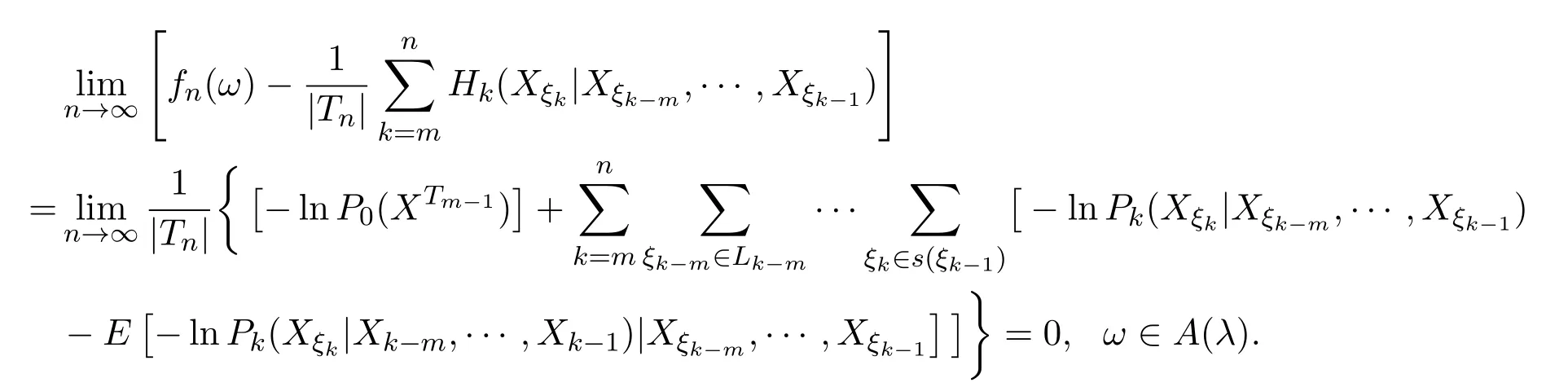
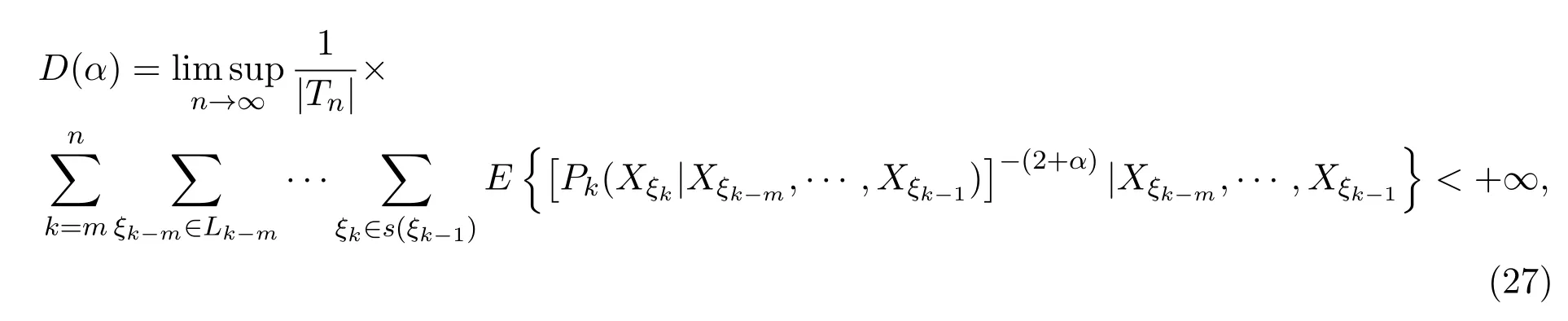
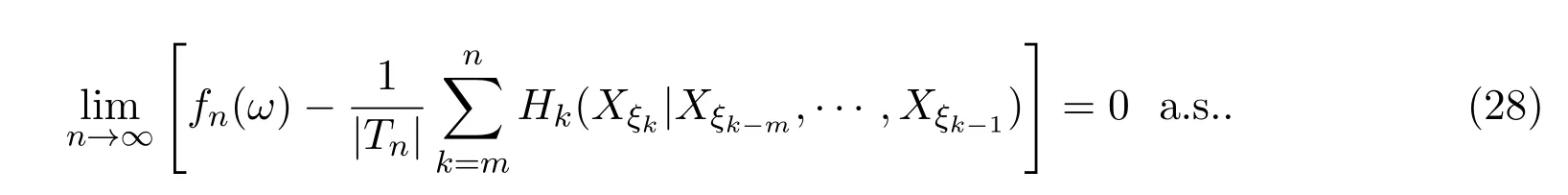
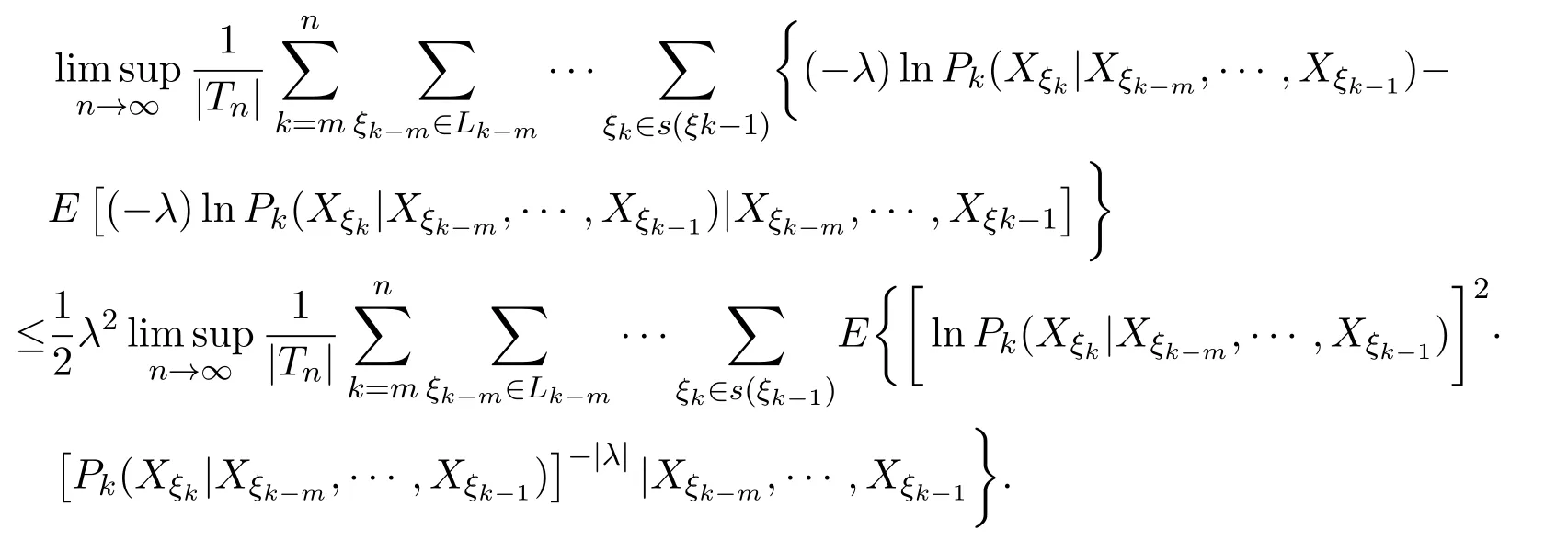
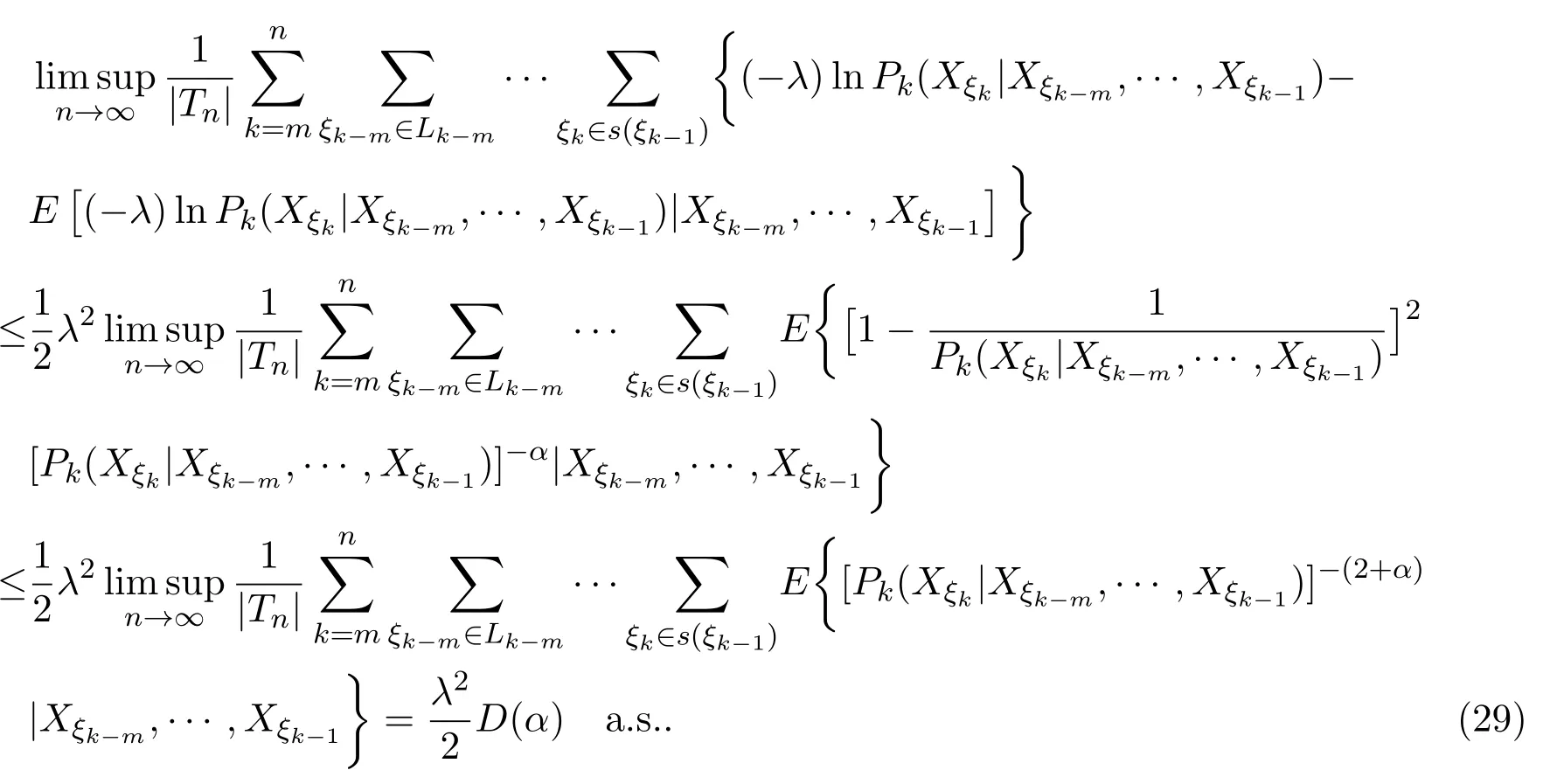
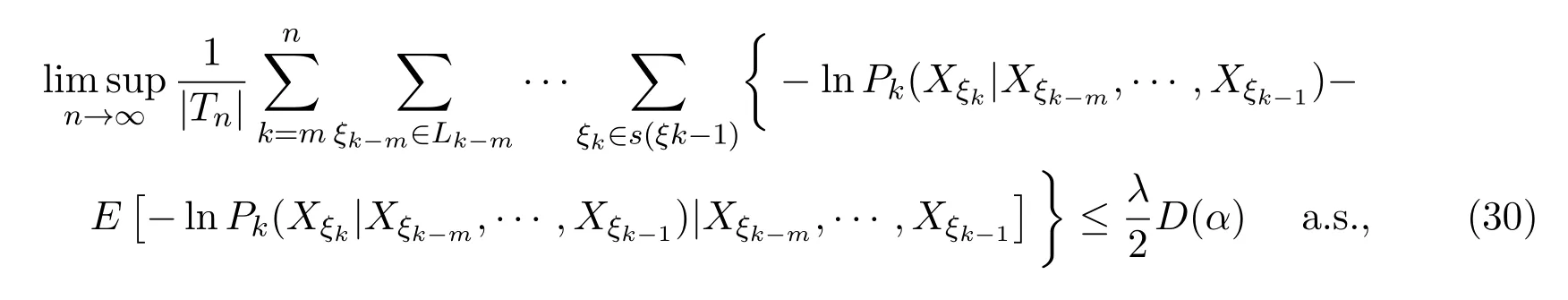
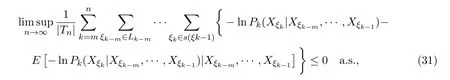
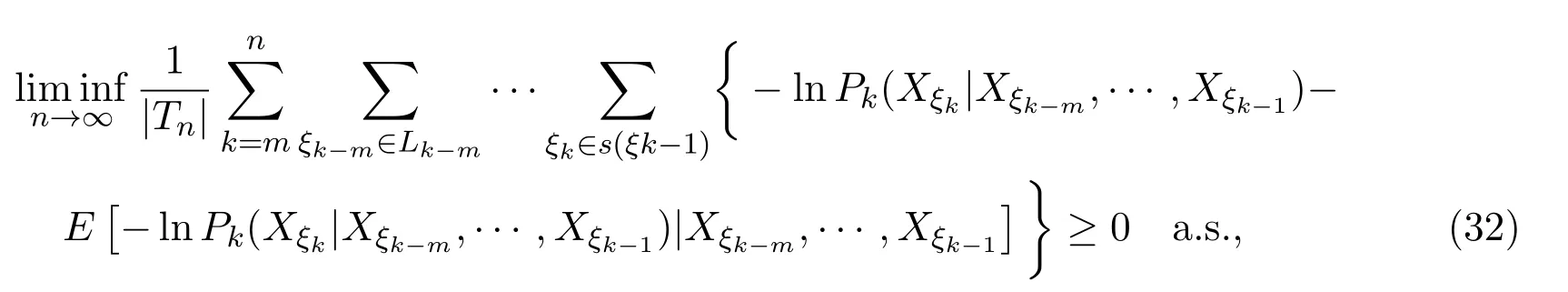
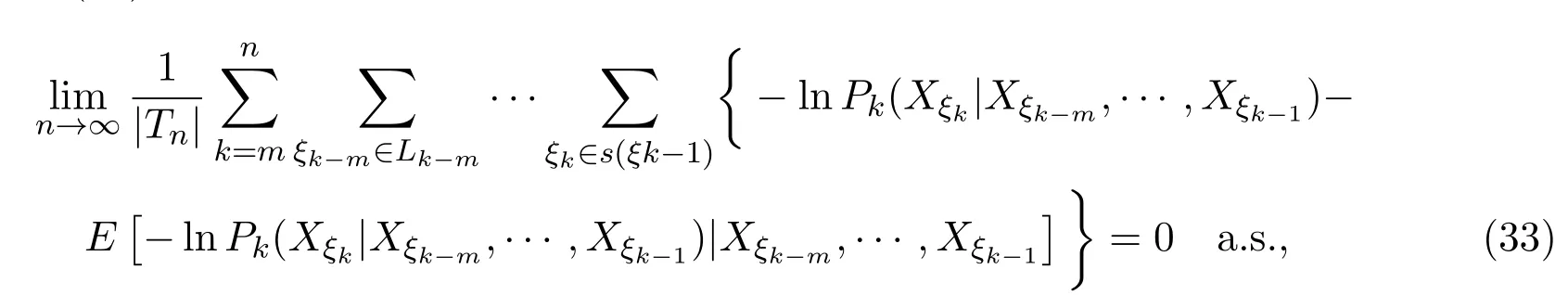
(College of Science,Hebei University of Technology,Tianjin300401,China)
