(2+1)维五次非线性薛定谔方程的无穷序列新解

阿如娜,套格图桑

(内蒙古师范大学数学科学学院,呼和浩特 010022)

(2+1)维五次非线性薛定谔方程的无穷序列新解

阿如娜,套格图桑

(内蒙古师范大学数学科学学院,呼和浩特 010022)

利用第二种椭圆方程的解和B¨acklund变换,获得了(2+1)维五次非线性薛定谔方程的新解.这些解是由Jacobi椭圆函数、三角函数、Riemann theta函数和指数函数组成的无穷序列新解.

第二种椭圆方程;B¨acklund变换;无穷序列新解

1 引言

许多文献研究不同设置下自聚焦和自散焦非线性时空效应[13].如锁模激光器[4],光纤和波导的脉冲传播[5],激光等离子体相互作用[67].物理学中许多现象是由非线性偏微分方程(NPDES)描述的.寻找非线性偏微分方程的解是解释其描述的自然现象的最有效方法之一.

(2+1)维五次非线性薛定谔方程[8](CQNLSE):

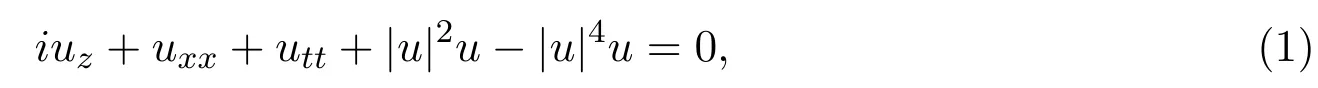
这里x和z是横向和传播坐标,t是所谓的减少时间.(2+1)维五次非线性薛定谔方程,是描述多种物理系统的数学模型.文献[8-9]给出了CQNLSE方程的一些固定解.

本文对(2+1)维五次非线性薛定谔方程进行了行波变换后,利用第二种椭圆方程的已知解和B¨acklund变换,获得了(2+1)维五次非线性薛定谔方程的无穷序列解,这些解包括Jacobi椭圆函数、三角函数、Riemann theta函数和指数函数解.

2 (2+1)维五次非线性薛定谔方程的解

对(2+1)维五次非线性薛定谔方程(1)作变换:

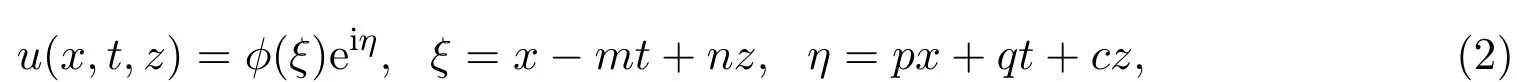
这里m,n,p,q和c是待定常数.

将(2)式代入方程(1),化简后得到如下常微分方程:

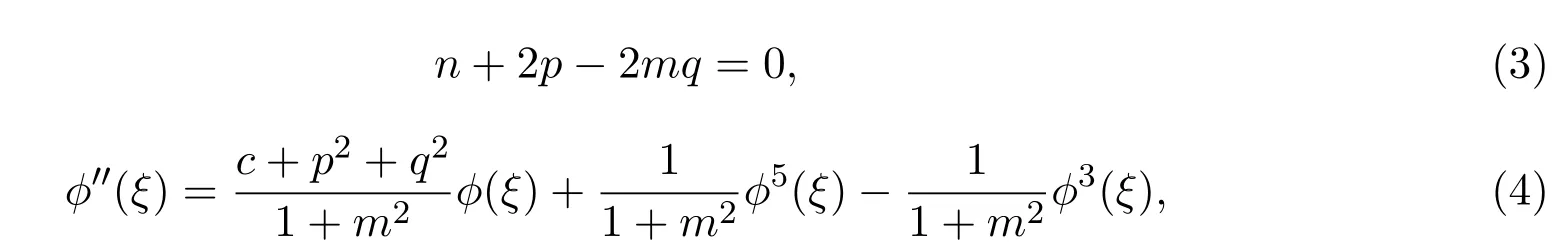
用ϕ′(ξ)乘方程(4)的两边,并对ξ积分一次后得到下列方程:

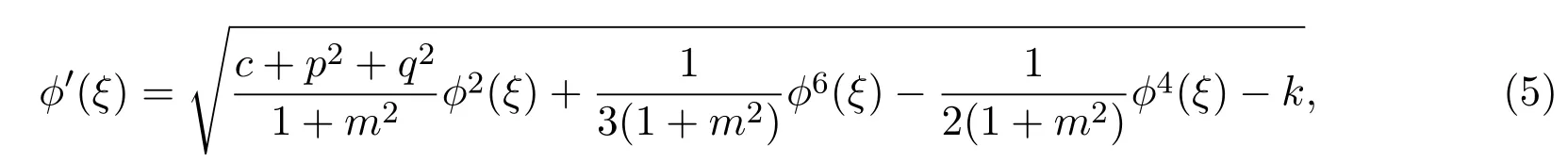
这里k是积分常数.

利用函数变换φ(ξ)=ϕ2(ξ),把方程(5)转化为下列常微分方程:

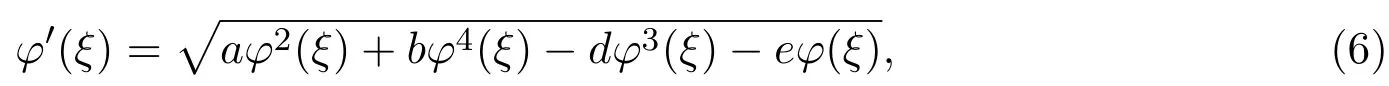
在方程(6)中取

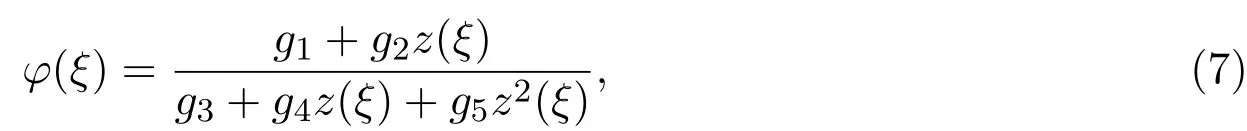
这里g1,g2,g3,g4和g5是任意常数,其中z(ξ)满足下列第二种椭圆方程:

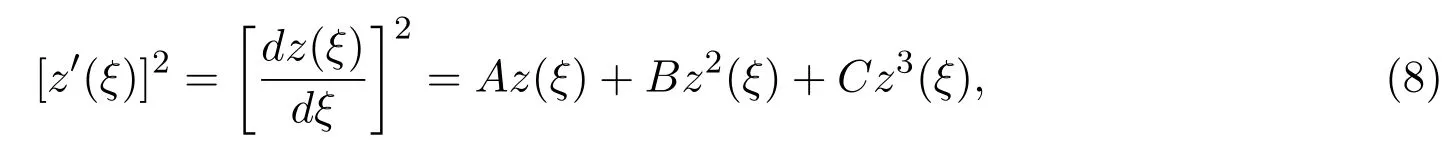
将(7)和(8)式一起代入(6)式,并令zi(ξ)(i=0,1,2,···,7)的系数为零后得到下列非线性代数方程组

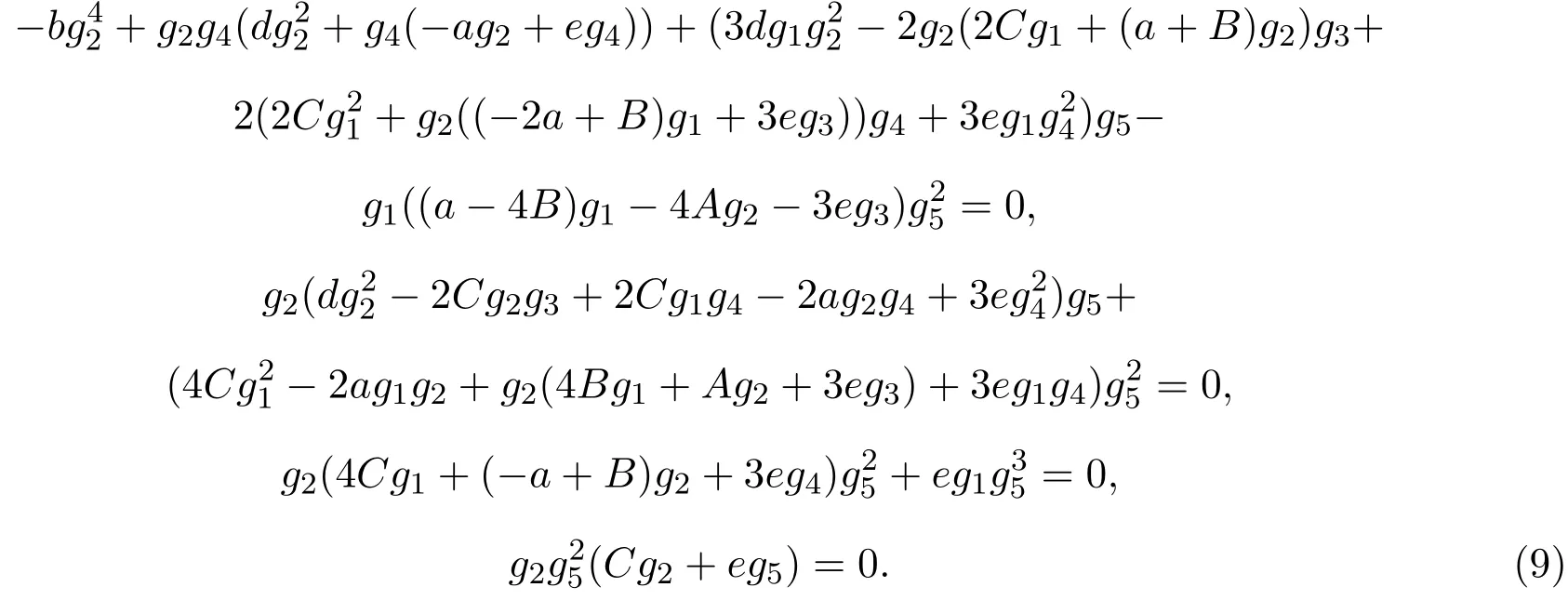
用符号计算系统Mathematica求出该方程组的下列解:

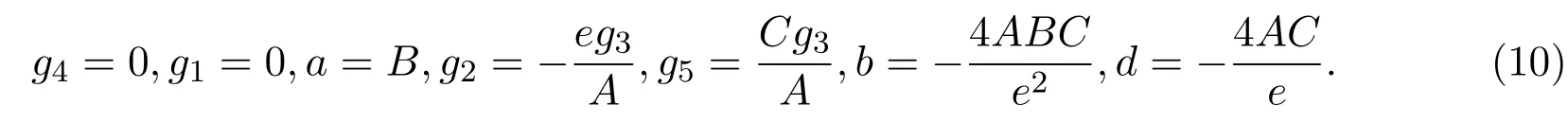
其中,A,B,C,e和g3为不全为零的任意常数,A,B和C是方程(8)的系数.

将(10)式代入(7)式后,得到方程(6)的下列形式解:

其中e为任意常数,A和C是方程(8)的系数,z(ξ)满足方程(8).

由形式解(11)和φ(ξ)=ϕ2(ξ)得到方程(4)的下列解:这里e为任意常数,A和C是方程(8)的系数,z(ξ)满足方程(8).

2.1 第二种椭圆方程的解

2.1.1 第二种椭圆方程 (8)的Jacobi椭圆函数解

文献[10]中获得了方程(8)的如下解:

当A=4,B=−4(1+k2),C=4k2时,(13)式是第二种椭圆方程(8)的解:

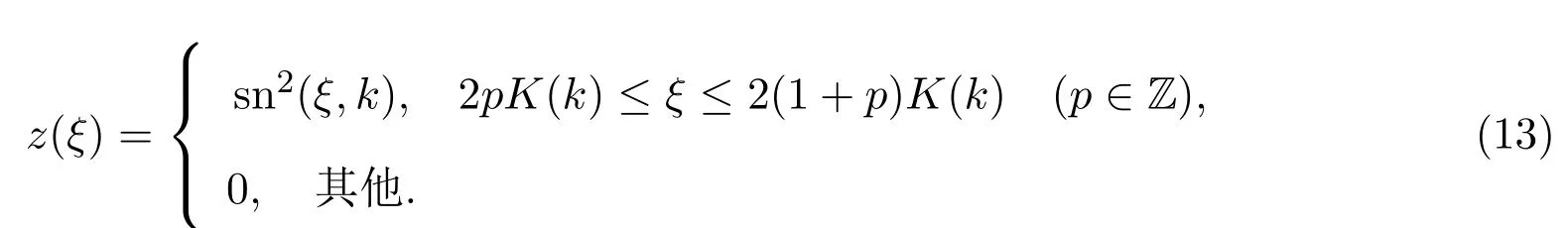
当A=4(1−k2),B=4(2k2−1),C=−4k2时,获得第二种椭圆方程(8)的如下解:

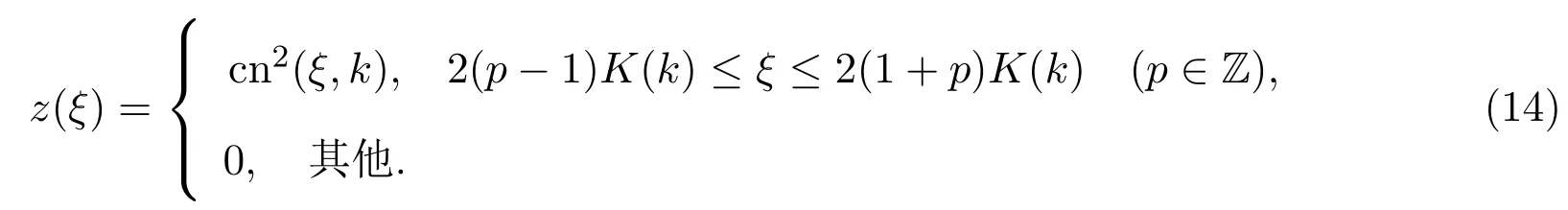
2.1.2 第二种椭圆方程(8)的Riemann theta函数新解

(15)式为 Riemann theta函数的定义,文献 [10]中获得了第二种椭圆方程 (8)的如下Riemann theta函数:

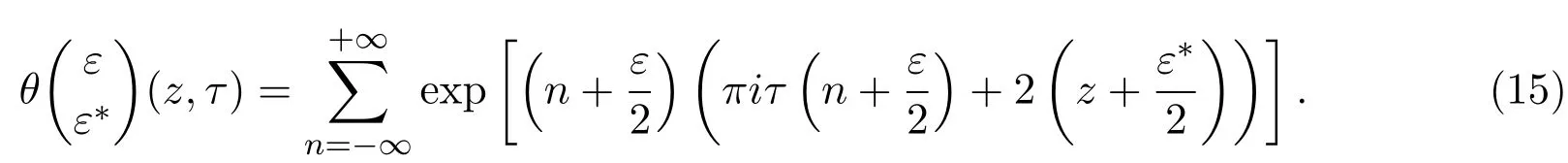
2.1.3 第二种椭圆方程 (8)的三角函数型解

由文献[10]可得到第二种椭圆方程(8)的如下三角函数解.

当C=0时,得到第二种椭圆方程(8)的下列解:

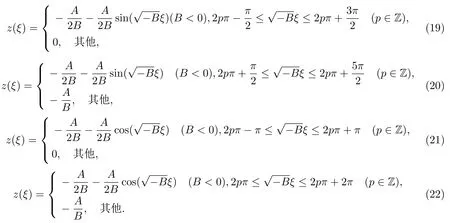
2.1.4 第二种椭圆方程 (8)的指数函数型解

文献[11]给出了方程(8)的下列解.

当B2−4AC=0时,可得到第二种椭圆方程(8)的下列解:

当A=C=0时,经计算获得第二种椭圆方程(8)的如下解:

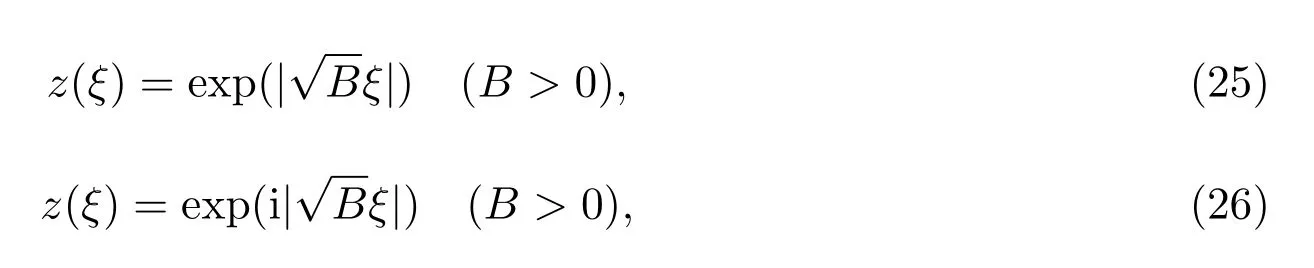
当A=0时,可得到第二种椭圆方程(8)的如下解:

2.2 第二种椭圆方程的B¨acklund变换

由文献[11]可知,如果zr−1(ξ)是第二种椭圆方程(8)的解,则下列zr(ξ)也是第二种椭圆方程(8)的解.

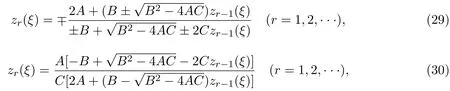
其中

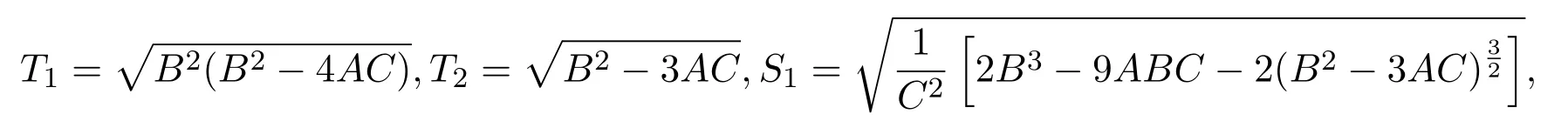
A,B和C是第二种椭圆方程(8)的系数.

情形 1(2+1)维五次非线性薛定谔方程的Jacobi椭圆函数型无穷序列解

将(13)式(或(14)),(12)式和(29)式代入(2)式,可得到(2+1)维五次非线性薛定谔方程的Jacobi椭圆函数型无穷序列解.

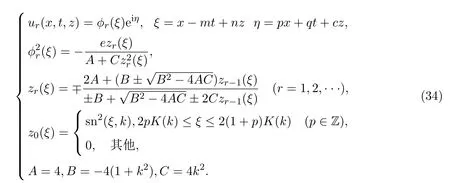
其中

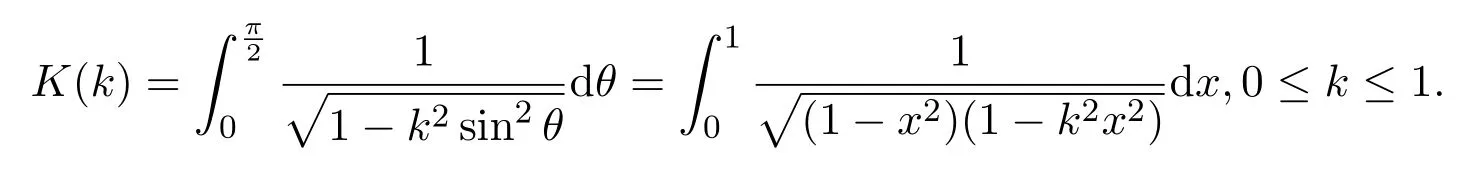
情形 2(2+1)维五次非线性薛定谔方程的三角函数型无穷序列解

通过下列叠加公式,可获得(2+1)维五次非线性薛定谔方程的三角函数型无穷序列解.

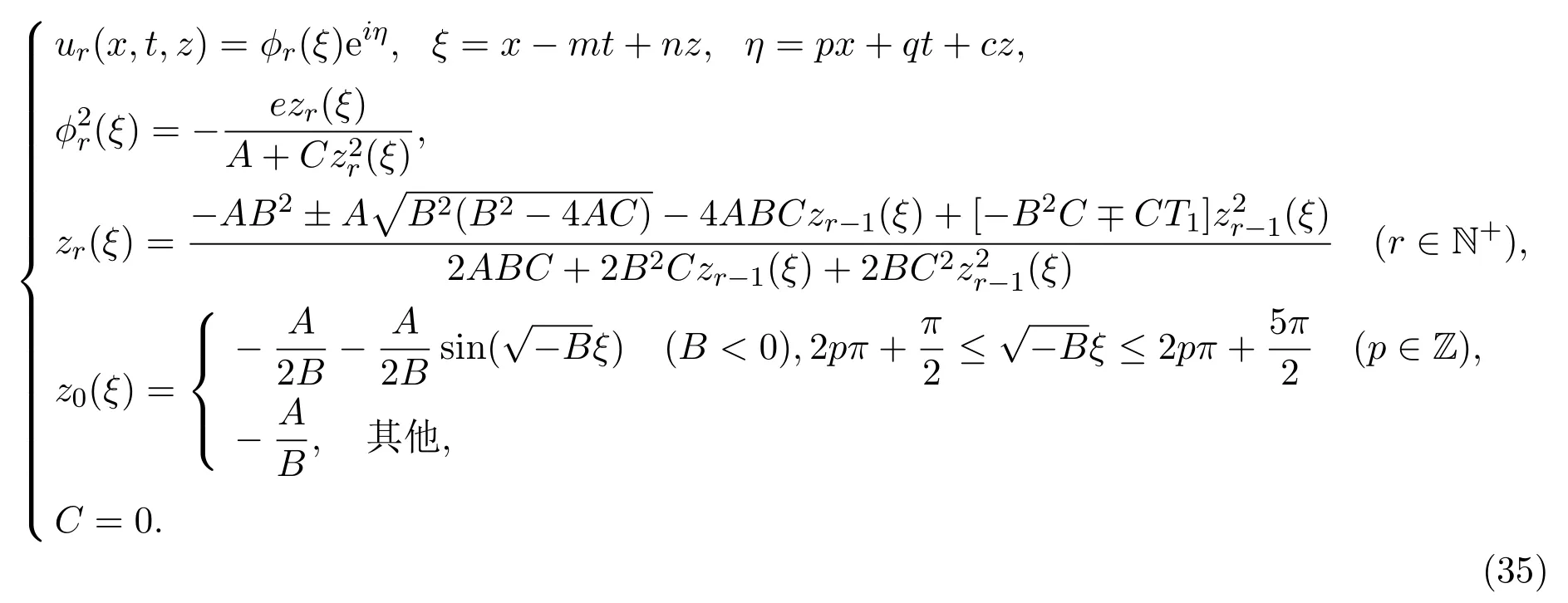
情形 3(2+1)维五次非线性薛定谔方程的指数函数型无穷序列解

由以下迭代公式,可构造(2+1)维五次非线性薛定谔方程的指数函数型无穷序列解.

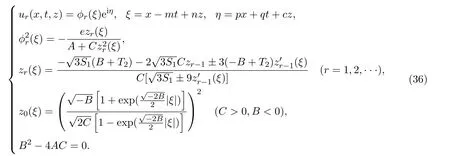
情形 4(2+1)维五次非线性薛定谔方程的Riemann theta函数型无穷序列解

通过以下公式,可获得(2+1)维五次非线性薛定谔方程的Riemann theta函数型无穷序列解.

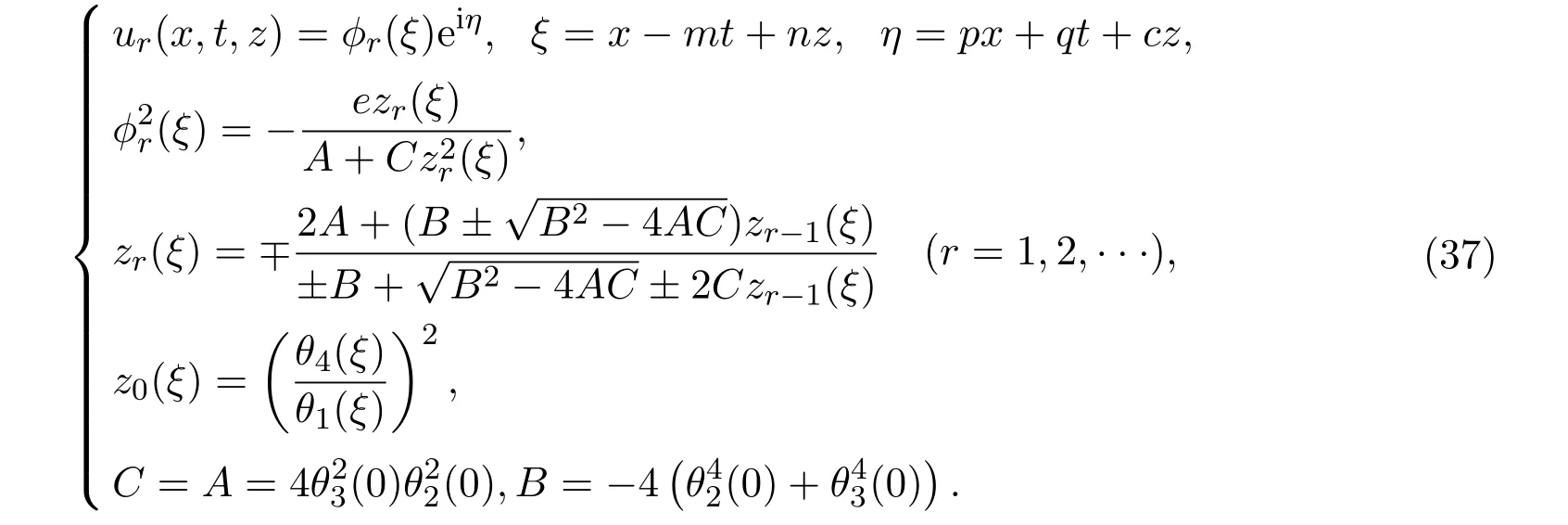
在以上的(34)-(37)式中,n,m,p,q是满足方程(3)的任意常数,A,B和C是方程(8)的系数.

3 结论

文献[12]获得了(2+1)维五次非线性薛定谔方程的双曲函数型和Jacobi椭圆函数型有限多个新解.本文利用行波变换、第二种椭圆方程的解和B¨acklund变换,构造了(2+1)维五次非线性薛定谔方程的由Jacobi椭圆函数、三角函数、Riemann theta函数和指数函数组成的无穷序列新解,所获得的解包括文献[12]所获得解.例如:文献[12]得到了方程(1)的下列形式解:

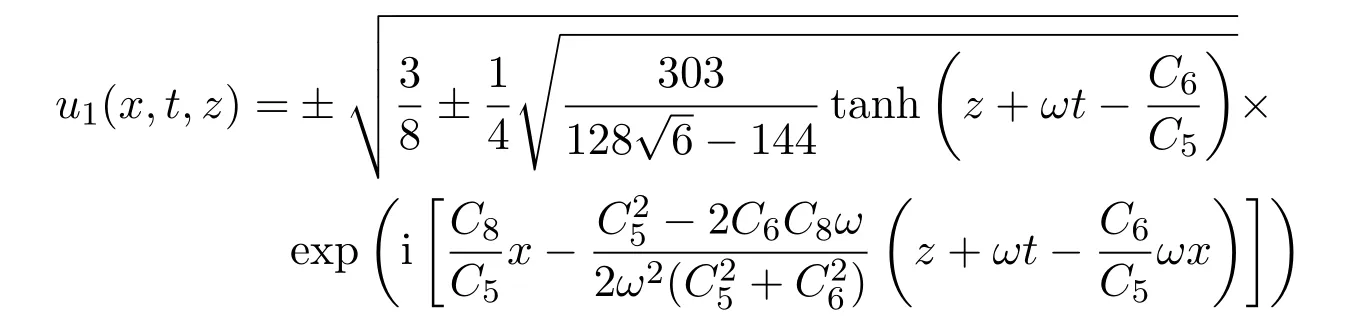
在迭代公式(34)中,当k→1时,sn(ξ,k)→tanh(ξ),便可得到方程(1)形如u1(x,t,z)的解.

参考文献

[1] Towers I N,Malomed B A,Wise F W.Light bullets in quadratic media with normal dispersion at the second harmonic[J].Phys.Rev.Lett.,2003,90:123902.

[2] Mihalache D,Mazilu D,Towers I,et al.Stable spinning optical solitons in three dimensions[J].Phys.Rev. Lett.,2002,88:073902.

[3] Mihalache D,Mazilu D,Lederer F,et al.Stable vortex tori in the three-dimensional cubic-quintic Ginzburg-Landau equation[J].Phys.Rev.Lett.,2006,97:073904.

[4] Moores J D.On the Ginzburg-Landau laser mode-locking model with fi fth-order saturable absorber term[J]. Opt.Commun.,1993,96:65-70.

[5] Mihalache D,Mazilu D,Bertolotti M,et al.Exact solution for nonlinear thin- fi lm guided waves in higherorder nonlinear media[J].J.Opt.Soc.Am.B,1988,5:565-570.

[6] Chen Y X,Lu X H.Spatiotemporal similaritons in(3+1)-dimensional inhomogeneous nonlinear medium with cubic-quintic nonlinearit[J].Commun.Theor.Phys.,2011,55:871-877.

[7] Liu H,Beech R,Osman F,et al.Periodic and solitary waves of the cubic-quintic nonlinear Schr¨odinger equation[J].J.Plasma Phys.,2004,70:415-429.

[8] Malomed B A,Crasovan L C,Mihalache D.Stability of vortex solitons in the cubic-quintic model[J]. Physica.D,2002,161:187-201.

[9] Quiroga-Teixeiro M,Michinel H.Stable azimuthal stationary state in quintic nonlinear optical media[J].J. Opt.Soc.Am.B,1997,14:2004-2009.

[10] 套格图桑,白玉梅.非线性发展方程的Riemann theta函数等几种新解[J].物理学报,2013,62(10):100201.

[11] 套格图桑.论非线性发展方程求解中辅助方程法的历史演进[M].北京:中央民族大学出版社,2012,6:251-255.

[12] Guo A L,Lin J.(2+1)-dimensional analytical solutions of the combining cubic-quintic nonlinear Schr¨odinger equation[J].Commun.Theor.Phys.,2012,57:523-529.

New in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation

Aruna,Taogetusang
(College of Mathematical Science,Inner Mongolia Normal University,Huhhot 010022,China)

In order to obtain a new in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation,this paper uses the solutions and B¨acklund transform of second kind of elliptic equations to construct the new in fi nite sequence solutions of(2+1)-dimensional cubic-quintic nonlinear Schr¨odinger equation consisting of Jacobi elliptic function,trigonometric function,Riemann theta function and exponential function.

the second kind of elliptic equation,B¨acklund transform,new in fi nite sequence solutions

O175.29

A

1008-5513(2014)04-0412-08

10.3969/j.issn.1008-5513.2014.04.011

2014-05-11.

国家自然科学基金(11361040);内蒙古自治区高等学校科学研究基金(NJZY12031);内蒙古自治区自然科学基金(2010MS0111).

阿如娜(1991-),硕士生,研究方向：孤立子与可积系统理论及其应用.

2010 MSC:35Q51