基于快速相关运算的卫星接收机矢量跟踪算法

谢 非，刘建业，李荣冰，徐 昭

（南京航空航天大学 导航研究中心，南京 210016）

基于快速相关运算的卫星接收机矢量跟踪算法

谢 非，刘建业，李荣冰，徐 昭

（南京航空航天大学 导航研究中心，南京 210016）

针对矢量跟踪过程中基带信号相关处理运算耗时较多的问题，提出了本地表及快速相关运算的优化处理方法，优化后的矢量跟踪环路中本地信号与输入信号的相关运算由耗时较多的浮点型运算转换为速度较快的位运算方式，降低了跟踪过程中的运算量，提高了矢量跟踪算法的运行速度。最后，利用实测的卫星中频信号对传统算法与优化算法进行了实验测试与性能分析对比，实验结果表明矢量跟踪算法对弱信号的持续跟踪能力优于传统标量跟踪方法，优化后的算法和原矢量跟踪算法相比信号处理时间约节省30%，有效改善了卫星接收机矢量跟踪算法中基带信号的处理效率。

卫星接收机；矢量跟踪；相关运算；弱信号

传统的卫星接收机结构中，各个通道对卫星信号的跟踪是相互独立的，不同跟踪通道分别复制相应卫星的PRN码与调制载波信号进行捕获、跟踪[1]，然后，通过解调出电文进行导航解算，从而计算出接收机的位置、速度等信息。传统的标量跟踪方式优点在于各个通道之间彼此独立，各自处理用户动态应力和接收机基准振荡频率漂移，环路通道间无信息交流，也不会互相干扰，但却忽略了卫星信号与接收机位置、速度之间固有的相关性。事实上，不同卫星到同一用户的几何位置关系决定了接收机基准振荡频率漂移在各个不同信号通道中会引入相同的频率干扰，动态应力作用在不同通道之间也是共同的，因此，可以将不同通道信号的跟踪与导航解算通过一个卡尔曼滤波器联系在一起，使得卡尔曼滤波器根据各个通道输出的载波鉴别结果和码鉴别结果直接实现定位，再利用同一个定位结果控制各通道的数字控制振荡器，实现对多个通道卫星信号的联合跟踪，降低环路的噪声带宽与提高环路对更高用户动态应力的容忍能力，保持更好的信号跟踪性能[2]。

James J.Spilker于1994年最早提出矢量延迟锁定环（Vector Delay Lock Loop,VDLL）的概念，将码环的跟踪与导航解算联系起来，可提高接收机对弱信号的跟踪能力[3]。近年来，国内外也逐步开展了对矢量跟踪的研究，美国Auburn大学的Matthew对标量跟踪与矢量跟踪进行比较，提出了两种不同模型结构的矢量跟踪算法，并对其在低信噪比环境下的性能进行了比较分析[4]。德国Munich大学Thomas Pany所在团队开展了VDLL与VFLL方面的研究，并进行了由户外转换到户内环境的接收机跟踪实验，实验过程中由传统跟踪模式切换到矢量跟踪模式下，在信号受到阻塞干扰后仍能恢复跟踪状态[5]。另外，加拿大Calgray大学将矢量跟踪与深组合研究相结合，进行了弱信号环境下的实验与分析[6]。

目前的卫星软件接收机除了射频信号到数字中频的转换使用硬件实现外，其他所有的处理，包括捕获、跟踪等基带信号处理都在通用PC或DSP上使用软件实现[7]，在这两种平台上开展矢量跟踪算法研究，每个周期时间内均要进行一次本地信号的生成运算，并且要完成各个跟踪环路中的相干积分运算，所耗时间较多。本文在多通道矢量跟踪模型设计研究基础上，为了提高这种依靠指令执行处理平台下的矢量跟踪算法处理速度，提出了基于快速相关运算规则的矢量跟踪优化处理方法，从而减小了矢量跟踪算法实现过程中信号处理的运算量，提高了跟踪环路的处理速度。

1 多通道矢量跟踪模型及滤波研究

1.1 矢量跟踪原理及模型结构

矢量跟踪方法与传统标量跟踪方法的主要区别在于对环路信号的控制方式不同，传统的软件接收机跟踪环路采用分散式的跟踪方式，各通道之间由相互独立的跟踪环路并行处理，并将相应的伪距测量值送入导航滤波器，从而估计出用户的位置、速度、钟差信息，总体结构图如图 1(a)所示，标量跟踪方式中解算出的导航信息处理为开环状态，对环路本地信号无反馈控制。矢量跟踪模式中，各通道间信号的联合跟踪一般通过Kalman滤波器或EKF滤波器来完成，各路卫星信号的相位及频率误差被作为接收机位置、速度变化量及钟差、钟差变化率等状态的观测矢量，根据导航状态与卫星星历数据对接收信号的频率和相位进行估计，并将估计信息送入本地信号发生器的数字控制振荡器（NCO），从而实现对各路卫星信号的联合跟踪，其模型结构如图1(b)所示。

图1 传统标量跟踪与矢量跟踪环路框图比较Fig.1 Comparison of the traditional tracking loop and VDFLL block diagram

1.2 矢量跟踪环路滤波器设计研究

设计矢量跟踪环路滤波器时，采用间接滤波方法，利用系统状态量（用户位置、速度、钟差及钟差漂移）的误差量作为状态，设为：

观测量为由所有可见星通道的码环鉴相器输出得到的伪距预测偏差，以及载波鉴频器输出的频率预测偏差所组成的矢量，预检测积分时间选择为1 ms，即滤波器迭代的k时刻与k+1时刻之间间隔为1 ms，假设用户在低动态下运动，则系统离散状态方程和观测方程分别为：

其中，Γk-1为系统噪声驱动阵，Wk为系统动态噪声序列，Vk为观测噪声序列；φk,k-1为tk-1时刻至tk时刻的一步转移阵，具体表达式如式(3)所示：

码环鉴别器的基本功能是让码环朝着超前支路功率与滞后支路功率相等的方向上调整码相位，考虑到码环鉴别器的运算量和性能，采用线性度较好的归一化超前减滞后功率鉴别器，其鉴别公式为：

由于码鉴相器输出δcode为k时刻某颗可见星1 ms长度的采样信号中伪码与本地即时码的相位偏差，而本地码的相位等于上一时刻输入信号伪码相位的估计值，因此，这种相位偏差实质上为k时刻输入信号的伪码相位与k-1时刻的相位估值之差，因此，由码相位偏差估计的伪距预测偏差量可以通过下式推算出来：

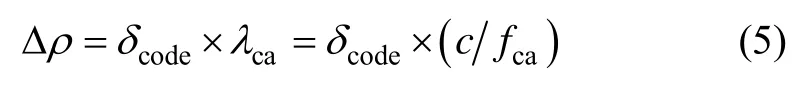
其中，c是光速，λca为C/A码波长，fca为基准码频率，IE和QE分别为同相与正交支路的超前码相关积分值输出，IL和QL分别为同相与正交支路的滞后码相关积分值输出。

载波环接收的为已剥离C/A码的调制导航数据的连续信号，由于卫星和接收机之间的相对运动会产生多普勒频移，使得接收到的卫星信号调制载波的频率发生偏移，而载波鉴频器通过检测复制载波与输入载波之间的频率差异，使两者的频率保持一致，利用鉴频器输出可估计出伪距率测量偏差，如公式(6)所示。

利用各通道码环估计的伪距预测偏差与载波环估计的载波频率预测偏差矢量作为观测量，建立与系统状态量之间的量测关系，相应的观测矩阵如下：

在Kalman滤波过程中，观测矩阵H中所包含的单位径向矢量需要由卫星位置和用户位置确定，具体可参考文献[8]。因此，在切换到矢量跟踪模式处理前，需要采用传统的跟踪方式跟踪一段时间，从导航电文中解译出星历参数后，可为矢量跟踪提供卫星与用户状态解算信息，此时可切换至VDFLL工作模式下。

1.3 矢量跟踪环路信号反馈控制研究

在完成跟踪环路信号特征量与接收机自身状态的信息融合之后，可利用用户接收机与卫星之间的相对位置变化及运动速度变化量预测出接收信号的相位变化及多普勒频率变化量，从而实现对下一时刻本地信号（码、载波）相位和频率的估计与控制，具体可通过以下公式计算：

为了进一步提高矢量跟踪算法的处理速度，研究了基于位运算规则的矢量跟踪环路信号优化处理方法，并进行了算法运算量分析。

2 基于快速相关运算矢量跟踪算法

在矢量跟踪环路的信号处理流程中，首先要将输入信号与对齐的本地载波相乘，对输入信号中的调制载波进行解扩，接着与三路本地码完成相关与积分运算，因此每个周期时间内均要完成一次本地载波信号与伪码的生成运算，为了节省本地信号的生成时间，设计了本地载波表与码表的存储与应用方法。

2.1 本地载波表与码表设计

为了提高矢量跟踪环路的处理速度，使用了载波表与码表预存了本地载波信号与本地C/A码信号。载波表纵轴表示中频附近-500～500 Hz的载波频率，并以每0.5 Hz为步长递增，共2001个离散频率，载波表横轴代表了长度为2 ms的（共16368×2=32736个）离散采样点，也反映了载波的相位信息，表中存储的数值为计算得到的载波三角函数值，数据存储格式为双精度类型。码表的纵轴代表了32颗星星号，横轴表示一个码周期对应的采样点数，从而将原来的 1023个码相位按采样频率进行了离散化，码表单元格中则存储了相应伪码的双极性量化值，此外，载波表与码表的各行存储值均从0相位开始存储。

当矢量跟踪环路中需要产生本地载波及本地码信号来完成与输入信号的相关运算时，可利用预存的载波表及码表进行查表搜索，找到频率与相位都最为接近的点作为起始点读取与生成本地载波信号，再与输入信号进行相关，同时记录该时刻载波信号读取的相位值，以便在下一周期内进行调整。本地码的读取方式与载波信号较为相似，不同之处为捕获到的码相位精度较高，生成每周期本地码时，对相位的调整较小。

2.2 基于快速相关运算规则的矢量跟踪算法

由于载波表中预存的载波信号值均使用浮点数进行存储，因此，在处理环路信号相关运算时，运算量仍然较大，为了进一步提高相关运算的处理速度，本文对矢量跟踪过程中的相关运算进行了优化，首先对连续的载波信号进行量化处理，如图2所示，量化后的载波信号利用±1、±2来表示。

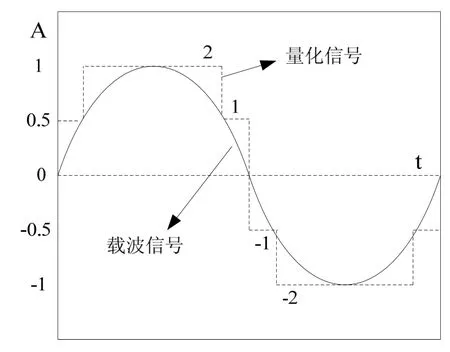
图2 载波信号量化方法Fig.2 The method to sample a sine wave

接着，为了使本地信号与输入信号可以通过位运算方式完成相关处理，将载波表与码表中的浮点型数据简化为由符号位和幅值位组成的二进制数据，简化方式如图3(a)及图3(b)所示。另外，输入的卫星中频信号采样值也需预先进行简化处理，处理方式如图3(c)所示，简化后的信号将原有的±1、±3量值利用一个符号位与幅值位进行保存。最后再将原有的相关运算由64位浮点型运算转换为位运算处理，以减小相关处理的运算量。

图3 输入信号与本地信号的简化处理Fig.3 Simplifications of the input signal and the local signals

在完成以上信号的简化处理后，需进行本地信号与输入信号相关运算的优化处理，利用位运算的快速处理优势，将本地信号与输入信号按照如图4所示的快速相关运算规则完成并行相关运算处理。对简化信号的快速相关处理方法为先将简化后输入信号与本地载波信号进行异或相乘，结果见图4 (a)所示，其中符号位由图3(a)和图3(b)中的符号位异或相加所得，高幅值位与图 3(c)中简化输入信号的幅值位相同，低幅值位与图 3(a)中简化载波信号的幅值位相同，当本地载波频率与相位同输入信号中载波严格对齐时，完成输入信号中调制载波剥离的混频处理。

图4 利用简化信号的快速相关运算规则Fig.4 Fast correlation rules of the simplified signals

将输入信号与本地载波信号混频后，再利用图4(a)中转换结果与本地简化伪码(图3(b))相关，完成对输入信号中调制码的解扩处理，最终相关结果见图4(b)所示。简化码与混频信号的快速相关规则为：将图3(b)与图4(a)中符号位经异或运算后得图4 (b)中的符号位结果，其高幅值位和低幅值位与图4(a)中的高、低幅值位相同，最后，对一个码周期时间内的相关数据进行累加求和。

位运算方法通过将两个浮点型数据的传统相关运算转化为两个位数据的异或运算及复制，优化了矢量跟踪环路中的相关处理过程，节省了运算所耗时间，对1 ms数据的相关运算量进行比较，比较结果如表1所示，从输入信号分别与本地载波及本地伪码信号相关时间统计来看，优化后的快速相关运算方法可平均节省共约2.384 ms的相关运算时间。

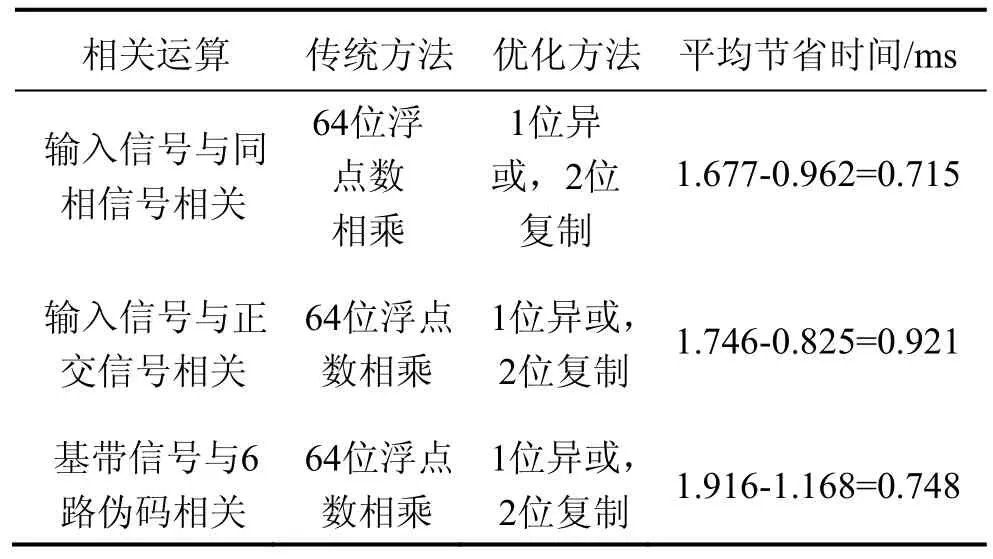
表1 传统相关方法与优化方法比较Tab.1 Comparison of the traditional correlation method and the optimized method

最后，再分别将快速相关累加结果送入码和载波鉴别器，估算出矢量跟踪环路滤波器的观测量，经滤波后反馈控制各卫星通道的数字压控振荡器，从而使得本地复现的伪码及载波信号与输入信号中调制信号时刻保持同步。

3 实验与分析

为了验证矢量跟踪算法及其优化方法的正确性与弱信号环境下的工作性能，利用实验室内部的GPS中频信号采样器，进行了户外-户内-户外条件下的实测数据采集，通过户内外环境信号强弱的变化来进行矢量跟踪环路的性能测试。

从图5中标量与优化矢量跟踪解调出的导航电文结果来看，当信号初始阶段于户外采集时，卫星信号强度较大，此时，传统标量跟踪方法与矢量跟踪两种方法均可对环路保持跟踪，但在采样器天线转移到信号较弱的户内环境以后（60～80 s），信号载噪比大大降低，传统标量跟踪环路开始出现失锁现象，即使后续重新返回户外也仍需进行重捕操作后方可恢复跟踪状态，而矢量环路由于借助了接收机位置、速度及星历信息的辅助，在信号失锁后仍能维持输出较为准确的多普勒频移特征量，如图6所示，从而使得卫星信号恢复以后，矢量环路可利用预测的频率信息较快恢复环路跟踪状态，有效的节省了重捕时间，提高了接收机的跟踪性能。

图5 标量跟踪与优化矢量算法输出导航电文结果Fig.5 Navigation message of scalar and optimized vector tracking results

图6 标量与矢量跟踪估计多普勒频移对比图Fig.6 Comparison of Doppler estimation of scalar and vector tracking methods

当采样器天线移至室内以后，由于跟踪环路出现失锁状态，因此对其输出的观测量进行屏蔽，即Zk置为0，从kalman滤波方程来看，此阶段其状态校正量为0，如式(11)所示，整个过程中优化矢量跟踪与标量跟踪定位误差对比结果见图 7，其中标量环路失锁后接收机定位误差大大增加，而矢量跟踪误差则保持在限定范围之内。

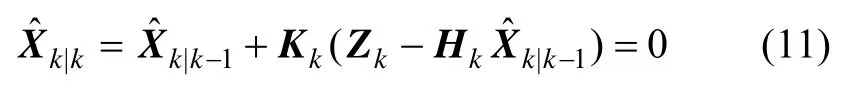
图7 优化矢量跟踪与标量跟踪定位误差对比Fig.7 Comparison of position errors estimated by optimized vector and scalar methods

最后，为了评估优化算法的运行速度，测试并记录了传统标量跟踪方法、原矢量跟踪算法与优化后的矢量跟踪算法对多通道信号联合跟踪所耗费的时间，实验利用实际采集的中频数据进行测试，测试结果见表2所示。由表2可以看出，常规矢量跟踪算法较标量跟踪方法耗时有所增加，而优化后的矢量跟踪算法则有效提高了常规矢量跟踪中的信号处理效率，由表2中数据可知约提高30.41%。

表2 传统方法与优化方法耗时比较Tab.2 Comparison of computation time between the traditional method and the optimized method

4 总 结

本文针对矢量跟踪算法中耗时较多的本地信号生成及相关运算部分，研究了利用载波表及码表预存与查表的方法，直接生成本地信号，并进一步提出了基于快速相关运算的矢量跟踪算法，将原有的双精度浮点数运算转换为位运算。从实测数据的跟踪实验结果来看，矢量跟踪算法相对于传统的标量跟踪方法具有环路信号失锁后重恢复跟踪能力的优点，节省了重捕获时间。此外，优化方法相对于原矢量跟踪方法在环路信号的处理效率上约提高30.41%，有效减小了环路跟踪过程中信号相关处理的运算量。

（References）：

[1]曾庆喜，唐琳琳，王庆，等.GPS软件接收机宽载噪比载波频率精确捕获策略[J].中国惯性技术学报，2013，21(4)：500-506.ZENG Q X,TANG L L,WANG Q,et al.Acquisition of fine carrier frequency under wide carrier-to-noise ratio in GPS software receivers[J].Journal of Chinese Inertial Technology,2013,21(4):500-506.

[2]Lashley M,Bevly D M.Comparison of traditional tracking loops and vector based tracking loops for weak GPS signals[C]//Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation.2007:570-576.

[3]Spilker J J.Fundamentals of signal tracking theory[M]// Global Positioning System:Theory and Applications.Washington,DC:AIAA,Inc.,1996.

[4]Lashley M,Bevly D M,Hung J Y.A valid comparison of vector and scalar tracking loops[C]//IEEE/ION Position,Location,and Navigation Symposium.2010:464-474.

[5]Pany T,Eissfeller B.Use of a vector delay lock loop receiver for GNSS signal power analysis in bad signal conditions[C]//IEEE/ION Position,Location,And Navigation Symposium.2006:893-902

[6]Petovello M G,Lachapelle G.Comparison of vectorbased software reciver implementations with application to ultra-tight GPS/INS integration[C]//The 19th International Technical Meeting of the Satellite Division of the Institute of Navigation.2006:1790-1800

[7]曾庆喜，王庆，王浩为，等.基于DSP的GPS软件接收机关键技术研究与实现[J].仪器仪表学报，2009，30(6)：1251-1255.ZENG Q X,WANG Q,WANG H W,et al.Research and realization of key technology for software GPS receiver base on DSP[J].Chinese Journal of Scientific Instrument,2009,30(6):1251-1255.

[8]Lashley M,Bevly D M,Hung J Y.Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics[J].IEEE Journal of Selected Topics in Signal Processing,2009,3(4):661-673.

[9]Zhao S H,Akos D.An open source GPS/GNSS vector tracking loop[C//International Technical Meeting of the Institute of Navigation.2011:1293-1305.

[10]Li H,Yang J S.Analysis and simulation of vector tracking algorithms for weak GPS signals[C]//2nd international Asia Conference on Informatics in Control,Automation and Robotics.2010:215-218.

[11]Edwards W L,Clark B J,Bevly D M.Implementation details of a deeply integrated GPS/INS software receiver [C]//IEEE/ION Position,Location,and Navigation Symposium.2010:1137-1146.

Vector tracking algorithm based on fast correlation operation in GNSS receivers

XIE Fei,LIU Jian-ye,LI Rong-bing,XU Zhao
(Navigation Research Center,Nanjing University of Aeronautics &Astronautics,Nanjing 210016,China)

Since the correlation processing of baseband signal in vector tracking loops of receivers take too much time,a local table design and an optimized algorithm based on a fast correlation method are proposed.In the optimized vector tracking loops,the floating point operation is replaced by bit arithmetic which is faster in correlation operation of local signal due to reduced computation in vector tracking process.Finally,the actual intermediate frequency GPS signal is used to test the performance of proposed algorithm.The experiment results indicate that the vector tracking algorithm is superior to the traditional tracking method in terms of continuous tracking capacity of weak signal,and the optimized method in GPS receiver can improve the baseband signal processing speed by 30% compared to the common vector tracking algorithm.

GNSS receiver;vector tracking;correlation operation;weak signal

U666.1

：A

1005-6734(2014)01-0094-06

10.13695/j.cnki.12-1222/o3.2014.01.019

2013-08-10；

：2013-12-24

国家自然科学基金（61273057,91016019）；航空科学基金（20100852010）；江苏高校优势学科建设工程资助项目；南航基本科研业务费专项科研项目资助

谢非（1983—），男，博士研究生，从事卫星导航技术与组合导航系统的研究。E-mail：xiefei@nuaa.edu.cn

联 系 人：刘建业（1957—），男，教授，博士生导师。E-mail：ljyac@nuaa.edu.cn