一种双惯导组合导航方法

刘为任，王 宁，刘国彬，年海涛，艾光彬

（1.天津航海仪器研究所，天津 300131；2.总装备部驻天津地区军事代表室，天津300131）

一种双惯导组合导航方法

刘为任1，王 宁1，刘国彬1，年海涛2，艾光彬1

（1.天津航海仪器研究所，天津 300131；2.总装备部驻天津地区军事代表室，天津300131）

一些舰艇装备两套或多套惯性导航系统。为提高这些舰艇导航信息输出的精度和稳定性，提出一种双惯导组合导航方法。从惯性导航系统的误差特性出发，分析了固定指北惯性导航系统和台体方位旋转惯导系统的误差特性，并根据两种惯导系统的不同误差特性，设计了 Kalman滤波组合导航控制方案，通过仿真验证了组合导航控制方案的效果。仿真结果表明，采用该方法后，在不增加任何硬件成本的基础上，能够提高导航信息输出精度和稳定性。例如，当陀螺漂移为0.002 (°)/h，加速度计零偏5×10-5g时，固定指北惯导24 h定位误差约为2.8 n mile，速度误差波动约0.2 kn，台体方位旋转惯导系统24 h定位精度约为1.7 n mile，速度误差波动约0.5 kn；当采用组合导航控制时，组合输出24 h定位精度约1.5 n mile，速度误差波动约0.15 kn。

固定指北；台体方位旋转；双惯导；组合导航

惯性导航系统是一种利用自身的惯性元件（陀螺和加速度计）来建立和保持空间基准，并测量载体运动，经过解算，输出载体的航向、航速、位置和姿态等数据的导航系统。它不仅为舰艇安全航行提供必要的导航信息，还为舰载武器等系统提供精确的姿态信息，因此，无论是弹道导弹核潜艇、攻击核潜艇、常规潜艇，还是航空母舰、驱逐舰、护卫艇和快艇，惯性导航系统都是其重要组成部分之一[1]。

大中型舰艇通常装备两套或者多套惯性导航系统，美国早期的核潜艇采用三套配置方案，后来随着惯性导航系统可靠性和精度的提高，调整为两套配置方案。采用两套或多套配置方案主要有两个优点，一是可提高舰艇的任务可靠性，当一套惯导故障时，另一套惯导仍可保障任务的继续执行；二是如果多套惯导采取分区布置，可就近为舰载武器等系统提供更精确的姿态信息，减小了船体变形对在武器等系统的影响。这种配置方案的主要缺点是需要更多的安装空间和资金投入。

当前对两套惯性导航系统的导航信息的使用主要有两种模式：一种模式是主从备份式，设置一套为主惯导，另一套为备份惯导，正常情况下，仅主惯导对外发送导航信息，只有在主惯导故障时，才有备份惯导对外发送导航信息；另一种模式是加权平均式，对外输出的导航信息采用两套惯导的加权平均值。

上述两种模式可提高惯性导航系统的任务可靠性，但对导航信息的输出精度没有根本的提高，为提高导航信息的输出精度，设计了基于不同旋转控制率的双惯导组合导航方法，使一套惯导系统工作在方位旋转状态，另一套工作在固定指北状态，利用两套系统的经纬度差作为观测量，应用 Kalman滤波方法估计出两套惯导的水平陀螺漂移并补偿[2]。该组合方法既可消除方位旋转带来的速度误差波动，又可使系统的定位精度提高约10%。

1 误差特性分析

1.1 固定指北惯导系统误差特性

静基座下固定指北惯导系统的误差方程为：

式中，δve、δvn为系统东、北向速度误差，α、β、γ为系统姿态误差角，δλ、δφ为系统经纬度误差，为东、北向加速度计零位，为东向、北向和方位陀螺漂移，R为地球半径，Ω为地球自转角速度。

式(1)为固定指北惯导系统的基本误差方程，当惯导元件误差为常值激励时，系统水平阻尼后，误差随时间变化曲线如图1所示。

1.2 台体方位旋转惯导系统误差特性

静基座下台体方位旋转惯导系统误差方程的表达形式同固定指北惯导系统误差方程一致，不同的是水平常值激励误差源被调制，此时，式(1)中的大小为：

图1 固定指北惯导导航参数误差曲线Fig.1 The north-azimuth INS errors curve

图2 台体方位旋转惯导导航参数误差曲线Fig.2 The rotation-azimuth INS errors curve

1.3 两种惯导系统误差特性比较

舰载武器系统对惯导导航信息的要求主要有两点：一是精度方面的要求，这是舰载武器系统子惯导进行传递对准的基础，二是导航信息稳定性方面的要求，导航信息波动幅度和频率对武器系统子惯导传递对准精度有一定的影响。因此，主要从导航信息精度和稳定性两个方面分析两种惯性导航系统的误差特性。

由图1和图2可以看出，在相同的常值误差源激励下，固定指北惯导系统输出信息精度相对较低，但平稳性较好；与此相反的是，台体方位旋转惯导采用旋转调制技术，通过对低频误差源的调制，提高了系统的定位精度和航向精度，同时也引入了又系统强制旋转而造成的速度误差以旋转周期和旋转周期二倍频波动，致使导航信息平稳性较差[4-5]。合理设计组合方案，可实现两种惯导系统的优势互补。

2 组合控制方法

2.1 组合方案

组合导航通常是指将具有不同特点的导航系统组合在一起，取长补短，用以提高系统的精度，常用的组合导航方案有惯导和卫导组合、惯导和多普勒计程仪组合等方案[6-7]。本文采用的是基于不同导航方式的两套惯导组合方案（如图3所示），由于两套惯导的导航控制方式不同，其误差特性也有所不同，据此可估计出两套惯导的水平陀螺漂移，提高系统导航精度[8]。

导航工作过程中，惯导1和惯导2的经纬度误差可实时观测，根据惯导系统误差方程，可利用kalman滤波方法，实时估计出两套惯导系统的水平陀螺漂移，以及由水平陀螺漂移造成的速度、经纬度和航向误差。

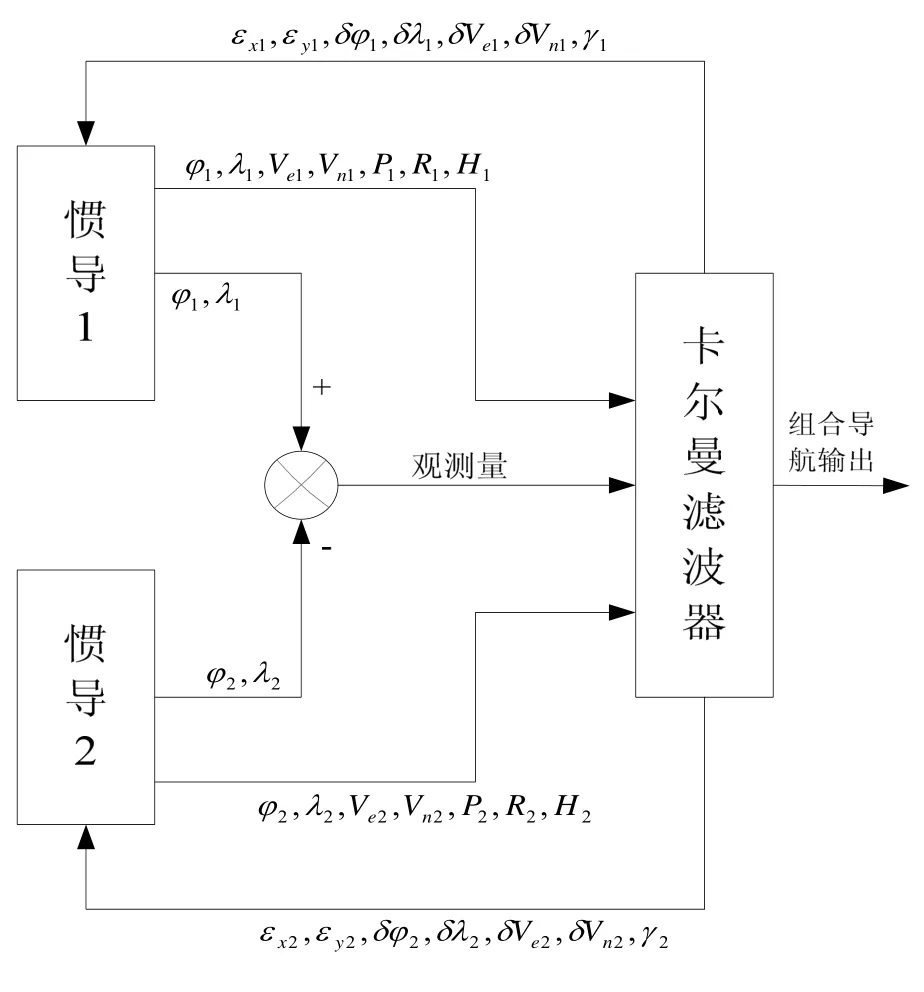
图3 双惯导组合导航结构框图Fig.3 Framework of dual INS integration navigation

2.2 状态方程

静基座下，惯导1和惯导2组合导航系统的状态空间表达式为：

式中：

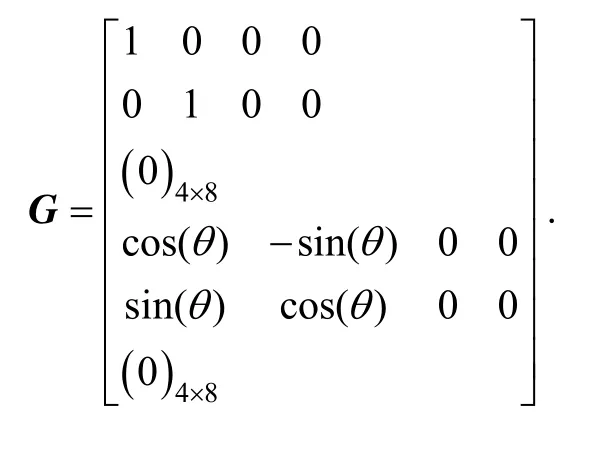
式中：R为地球半径，Ω为地球自转角速度。

2.2 观测方程

以惯导1和惯导2的经纬度误差作为观测量得到观测方程：

3 仿真分析

3.1 仿真条件

2）初始纬度为39°；

3）采样时间为0.1 s；

4）系统每两小时进行一次闭环校正，同时重置滤波器。

3.2 仿真结果及分析

由图1可见，当惯导系统工作在固定指北时，系统24 h的定位精度为2.8 n mile，速度误差波动小于0.2 kn；由图2可见，当惯导系统工作在台体方位旋转时，系统24 h的定位精度约1.7 n mile，速度误差波动约为0.5 kn；由图4可见，当采用组合导航控制时，系统24 h的定位精度约1.5 n mile，速度误差波动小于0.15 kn。

图4 双惯导组合导航参数误差曲线Fig.4 The integration navigation of dual INS errors curve

4 结 论

本文提出了一种基于不同导航方式的双惯导组合导航方法，针对固定指北惯导系统和台体方位旋转惯导系统导航信息的误差特性不同，设计了组合导航控制方案，通过仿真分析了组合导航控制方案的效果。仿真结果表明，组合系统即保持了指北惯导系统导航信息稳定性好的特性，又保持了旋转惯导系统导航信息精度高的特性。若加速度计零位为，陀螺漂移为0.002 (°)/h，则采用该方法后，组合输出的24 h定位精度提高约10%，水平速度误差波动幅度减小了约20%。

（References）：

[1]White D,Psota F.A precision navigation system for autonomous undersea vehicles[J].IEEE,1996:262-267.

[2]张科，刘海鹏，李恒年，等.SINS/GPS/CNS 组合导航联邦滤波算法[J].中国惯性技术学报，2013，21(2)：226-230.ZHANG Ke,LIU Hai-peng,LI Heng-nian,et al.SINS/ GPS/CNS integrated navigation federal filtering algorithm[J].Journal of Chinese Inertial Technology,2013,21(2):226-230.

[3]刘为任，唐艳，朱蕾，等.主惯导旋转调制对传递对准性能的影响[J].中国惯性技术学报，2011，19(2)：16-20.LIU Wei-ren,TANG Yan,ZHU Lei,et al.Effect of MINS rotation-modulating on transfer alignment[J].Journal of Chinese Inertial Technology,2011,19(2):16-20.

[4]Tucher T,Levision E.The AN/WSN-7B marine gyrocompass/navigator[C]//ION NTM 2000.Anaheim,CA,2000:348-357.

[5]袁保伦，饶谷音，廖丹.旋转式惯导系统得标度因数误差效应分析[J].中国惯性技术学报，2010，18(2) ：160-163.YUAN Bao-lun,RAO Gu-yin,LIAO Dan.Scale factor error analysis for rotating inertial navigation system[J].Journal of Chinese Inertial Technology,2010,18(2):160-163.

[6]Ramanandan A,Chen A,Farrell J A.Inertial navigation aiding by stationary updates[J].IEEE Transacation on Intelligent Transportation Systems,2012,13(1):235-248.

[7]Arasaratnam I,Haykin S.Cubature Kalman filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.

[8]Paul A S,Wan E A.A new formulation for nonlinear forward-backward smoothing[C]//IEEE Int.Conf.on ASSP.2008:3621-3624

Integration navigation method of dual INS

LIU Wei-ren1,WANG Ning1,LIU Guo-bin1,NIAN Hai-tao2,AI Guang-bin1
(1.Tianjin Navigation Instruments Research Institute,Tianjin 300131,China;2.Tianjin Military representative office of Armament Ministry,Tianjin 300131,China)

An integration navigation method of dual INSs was put forward to improve the navigation parameters precision and stability.The error characteristics of north-azimuth INS and rotation-azimuth INS were analyzed.An integration navigation method using Kalman filtering was designed based on different error characteristics of the two INS,and then was tested by computer simulation.The simulation result shows that the integration navigation method can improve navigation parameters precision and stability.For example,when the gyro drift is 0.002 (°)/h and the accelerometer bias is 5×10-5g,then the north-azimuth INS position error is 2.8 n mile/24h and the velocity error oscillation is about 0.2 kn,the rotation-azimuth INS position error is 1.7 n mile/24 h and the velocity error oscillation is about 0.5 kn,while the integration position error is improved to 1.5 n mile/24 h and the velocity error oscillation is reduced to about 0.15 kn.

north-azimuth;rotation-azimuth;dual INS;integration navigation;

U666.1

：A

1005-6734(2014)01-0001-04

10.13695/j.cnki.12-1222/o3.2014.01.001

2013-07-29；

：2013-11-20

海军武器装备预研项目（08330/1080）

刘为任（1973—），男，研究员，硕士生导师，研究方向为导航、制导与控制。Email：weirenliu@eyou.com