激光陀螺捷联惯导系统外场快速标定新方法

贾继超，秦永元，张 波，吴训忠

（1.西北工业大学 自动化学院，西安 710072；2.航天第十六研究所，西安 710100；3.空军工程大学工程学院，西安 710038）

激光陀螺捷联惯导系统外场快速标定新方法

贾继超1,2，秦永元1，张 波2，吴训忠3

（1.西北工业大学 自动化学院，西安 710072；2.航天第十六研究所，西安 710100；3.空军工程大学工程学院，西安 710038）

针对激光陀螺具有标度因数稳定、漂移误差变化小的特点，建立了适合激光陀螺捷联惯导系统的陀螺及加速度计组件简化误差参数模型，推导出了适合激光陀螺捷联惯导系统外场快速自标定的误差模型，设计了激光陀螺捷联惯导系统9位置系统级标定方法，并通过试验验证了该方法可快速准确的标定出加速度计组件的标度因数、安装误差、零偏及激光陀螺安装误差等 15个主要参数，方法简单易行。

激光陀螺捷联惯导系统；参数稳定性；系统级标定；误差参数辨识

通过系统级标定技术进行捷联惯性系统误差参数的快速估计与补偿，是解决参数性能保持期问题、提高系统精度的重要途径之一[1]。文献[2-3]的系统级标定方法，结合姿态矩阵，静态下以加速度计比力测量值在当地水平地理坐标系下的投影为观测量，经过静止—转动—静止的标定过程，可以标定出陀螺、加速度计组件的标度因数、安装误差角及零偏等全部 24个主要参数。文献[4]设计了一种多位置连续转动标定方案，通过测量每个位置静态导航状态下的速度误差，采用最小二乘法，全面辨识所有24个误差参数。文献[5]基于激光陀螺捷联惯导系统参数稳定性统计分析，建立了适合激光陀螺捷联惯导系统外场自标定的加速度计组件误差参数模型。以惯性组合转动后重新调平的水平姿态修正量以及静态下重力测量误差为观测量，不依赖外界方向姿态转角等基准信息，实现了加速度计组件主要误差参数在外场条件下的自标定，并给出了标定参数的修正方法。

本文在上述研究基础上，利用激光陀螺标度因数稳定、漂移误差变化小的特点，建立了适合激光陀螺捷联惯导系统外场快速自标定的简化误差参数模型，推导出了适合激光捷联惯导系统外场快速自标定的误差模型，提出了激光捷联惯导系统9位置系统级标定方法，并通过试验验证了该方法可快速准确的标定出系统各项误差系数。

1 误差参数标定模型

1.1 惯性组件误差模型

不考虑加速度计标度因数的非线性影响，加速度计组合的误差模型可写为：

激光陀螺具有标度因数稳定、零偏误差变化小的特点[5]，激光陀螺标度因数和零偏可作为外场自标定的基准，由安装误差引起的激光陀螺的误差模型如下：

从式(1)和式(2)可以看出，所建立的激光陀螺及加速度计组件简化误差参数模型一共包括 15个误差参数，较大多数文献中所建立的惯性仪表误差模型少了9个参数，有利于简化标定算法，缩短标定时间，更适合外场条件下的快速标定。

1.2 误差参数标定模型

文献[6]给出了导航速度误差与惯性仪表误差参数之间的代数关系，结合上节给出的惯性组件误差模型，可以推导出适合激光陀螺捷联惯导系统快速标定的误差模型如下式所示：

2 系统级标定方案设计

2.1 标定位置编排

本标定方法是基于激光陀螺捷联惯导多位置翻滚试验进行的，试验可分为静止—转动—静止三个阶段。首先在静止状态下对惯导进行解析粗对准；然后，按照预先设计的位置编排旋转惯导，在转动完成并静止后，以加速度计比力测量值在当地水平地理坐标系下的投影为观测量，作为导航误差观测量。

起始位置机体系大致指向东北天，启动激光陀螺捷联惯导系统；在第一个位置静止2 min后，按图1中所示方向转动到第二个位置；静止2 min后再转到第三个位置，按图1中位置编排依次进行；到第9个位置静止2 min后即可关闭系统，利用保存的加速度计和陀螺仪脉冲数据对系统15个误差系数进行标定。

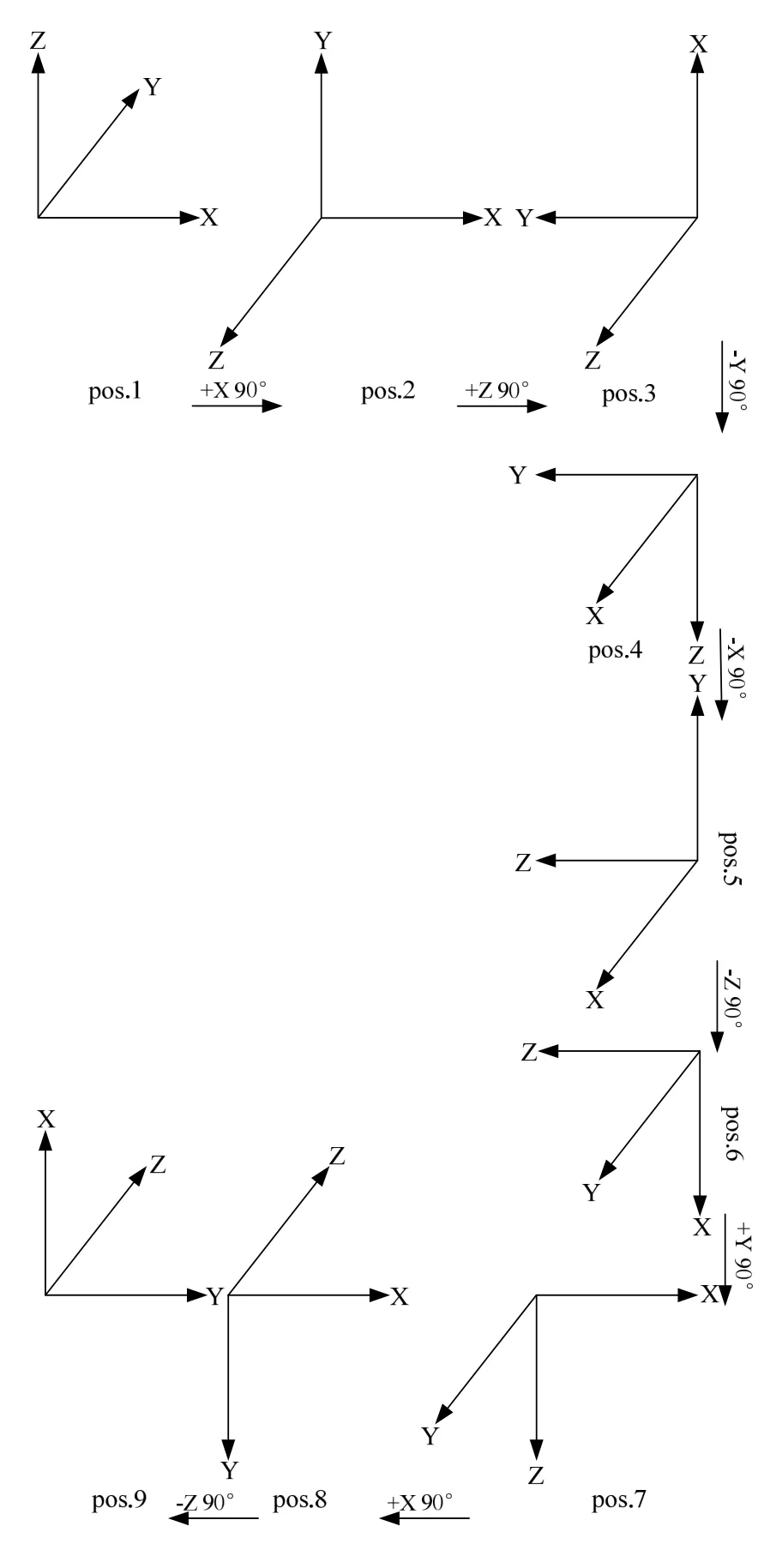
图1 9位置标定位置编排Fig.1 Nine-position calibration arrangement

2.2 系统误差系数确定

3 试验验证

试验采用的某型激光陀螺捷联惯导系统由三个激光陀螺和三个石英挠性加速度计等组成。试验过程中不采用任何转台，直接采用人工手动方式在平板上完成标定测试。在一次启动激光陀螺捷联惯导系统过程中做三组9位置试验。每组9位置试验需要时间在0.5h以内。试验结果如表1所示。

表1 9位置标定试验结果Tab.1 Test results of nine-position

表1第2列为三次9位置法标定结果的均值，第3列为三次9位置法标定结果的极差，第4列为利用传统标定方法标定出的基准值，第5列为9位置法相对于基准值的标定误差。表1中Mx、My、Mz分别为加速度计x、y和z的标度因数，从表1中可以看出，利用9位置标定方法和传统标定方法的标定结果精度相当，其中加速度计零偏最大相差 33μg，加速度计标度因数最大相差2.8×10-5，加速度计安装误差最大相差6.2″，陀螺仪安装误差最大相差5.4″。

4 结 论

本文从工程需要的角度出发，提出了一种适用于激光陀螺捷联惯导系统的9位置快速标定方法，该方法通过合理的位置编排，静态下以加速度计比力测量值在当地水平地理坐标系下的投影为观测量，经过静止—转动—静止的标定过程，可以标定出加速度计组件的标度因数、安装误差角、零偏及陀螺安装误差15个主要参数。通过实际系统进行标定发现，9位置标定与传统标定方法相比：标度精度相当，标定时间节约一半以上。本文提出的激光陀螺捷联惯导系统快速标定方案具有较高的工程应用价值。

（References）：

[1]Titterton D H,Weston J L.Strapdown inertial navigation technology[M].London,United Kingdom:Peter Peregrinus Ltd.,2004.

[2]Savage P G.Strapdown analytics[M].Maple Plain,Minnesota:Strapdown Associates,Inc.,2007.

[3]Zhang H,Wu Y,Wu M.A multi-position calibration algorithm for inertial measurement units[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu,Hawaii,2008.

[4]Xie Bo,Qin Yongyuan.Wan Yanhui.A-high-accuracy calibration method of optical gyro SINS[C]//3rd international symposium on Aeronautics and Astronautics.Harbin,2010:507-511.

[5]吴文启，张岩，张晓强，潘献飞.激光陀螺捷联惯导系统参数稳定性与外场自标定[J].中国惯性技术学报，2011，19(1)：11-15.WU Wen-qi,ZHANG Yan,ZHANG Xiao-qiang,PAN Xianfei.Parameter stability and outfield self-calibration of RLG-SINS [J].Journal of Chinese Inertial Technology,2011,19(1):11-15.

[6]杨晓霞，黄一.激光捷联惯导系统的一种系统级标定方法[J].中国惯性技术学报，2008，16(1)：1-7.YANG Xiao-xia,HUANG Yi.Systematic calibration method for laser gyro SINS[J].Journal of Chinese Inertial Technology,2008,16(1):1-7.

[7]张亮.激光陀螺捷联惯导系统的系统级标定方法研究[D].北京：中国运载火箭技术研究院，2007.ZHANG-Liang.Research on the systematic calibration method for laser gyro SINS[D].Beijing:China Academy of Launch Vehicle Technology,2007.

New fast systematic calibration method for RLG-SINS

JIA Ji-chao1,2,QIN Yong-yuan1,ZHANG Bo2,WU Xun-zhong3
(1.Department of Automatic Control,Northwestern Polytechnical University,Xi’ an 710072,China;2.16th Institute,China Aerospace &Technology Corp.,Xi’an 710100,China;3.College of Engineering,Air Force Engineering University,Xi’an 710038,China)

In view that RLG’s scale factor is stable,and its drift error has little change,a simplified error parameter model of gyro and accelerometer components is presented.The error model suitable for RLG-SINS fast outfield self-calibration is derived,and a nine-position systematic calibration method for RLG-SINS is designed.The experiments results show that the new method can rapidly calibrate the overall fifteen error parameters of RLG-SINS with high accuracy.In addition,this method is simple and feasible.

RLG-SINS;parameter stability;systematic calibration;error parameter identification

U666.1

：A

1005-6734(2014)01-0023-03

10.13695/j.cnki.12-1222/o3.2014.01.006

2012-6-21；

：2013-10-24

武器装备预研项目（51309040501）

贾继超（1977—），男，博士后，从事惯性导航技术研究。E-mail：jjcnwpu@sohu.com

联 系 人：秦永元（1946—），男，教授，博士生导师。E-mail：qinyongyuan@nwpu.edu.cn