基于状态参数可观测度分析的舰机传递对准自适应滤波方法

梁 浩，王丹丹，穆荣军

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.北京宇航系统工程研究所，北京 100076）

基于状态参数可观测度分析的舰机传递对准自适应滤波方法

梁 浩1，王丹丹2，穆荣军1

（1.哈尔滨工业大学 航天学院，哈尔滨 150001；2.北京宇航系统工程研究所，北京 100076）

针对舰机惯导传递对准过程中舰船机动受限、系统可观测性差等特点，提出了基于状态参数可观测度分析的自适应滤波方法。通过系统状态参数可观测性分析，量化各状态分量可观测程度，进而根据可观测度大小分组构造自适应调节因子，并采用滤波增益衰减法对观测度低的分量通道进行有效处理，以此来提高传递对准滤波算法的适应性和滤波估计精度。舰船模拟轨迹下仿真结果表明，基于状态参数可观测度分析的自适应滤波方法和常规方法相比，具有较高的精度和较快的收敛速度，对准精度由3′提高到2′，滤波估计收敛时间由15 min缩短至8 min。

舰载机；传递对准；可观测度分析；滤波增益衰减

舰船体积较大，在航行过程中机动形式受到限制，而当海洋环境比较恶劣时，舰船运动状态又会受到影响而变化不定[1-3]。因此，复杂多变环境下的舰机惯导传递对准成为近年来惯性技术领域研究的重点课题。从动基座传递对准研究的历史来看，为了提高传递对准精度、缩短对准时间，研究内容主要集中于各种传递匹配方法以及各种卡尔曼滤波模型的探讨[4-5]。因此，改进算法、设计合理的滤波器是提高对准效果的重要手段之一。

传递对准匹配方法主要分为计算参数匹配法和测量参数匹配法两类，不论采用何种匹配方法，传递对准状态分量的估计速度和精度主要取决于系统的可观测性[6]。状态分量可观测性的强弱用可观测度来衡量，目前，可观测度的分析方法主要有估计误差协方差阵的征值法和可观测矩阵的奇异值分解法[7-8]，前者要在Kalman滤波运算之后才能进行可观测度分析，而后者可以在滤波估计的同时进行可观测度计算。

本文以舰载机惯导传递对准为应用背景，建立了地理系下传递对准模型，给出了可观测度的计算方法，提出了一种基于可观测度分析的传递对准自适应调节滤波方法，并采用模拟轨迹对常规方法和改进方法进行了仿真对比和分析，验证了该方法的有效性和优越性。

1 地理系下传递对准模型

1.1 “变形角”定义

舰船甲板在不同种类因素影响下会产生不同形式的变形[9-10]，例如在舰体老化、温度变化、恒定载荷等因素作用下会产生静态变形，而在海浪冲击、舰体运动、舰内机械设备运作等因素影响下会产生动态变形，相关研究表明，舰船甲板变形量可达1°～1.5°，此外，舰载机惯导的安装误差角也会对惯导对准产生影响。为了便于进行传递对准估计精度分析，我们定义甲板“变形角”的概念，即“变形角”为机载惯导安装误差角和甲板变形角之和。

甲板动态变形可用由随机力激发的随机变量来描述，即可采用白噪声激励的二阶 Markov过程来模拟甲板的动态变形。设三向变形彼此独立，则甲板动态变形角模型如下：

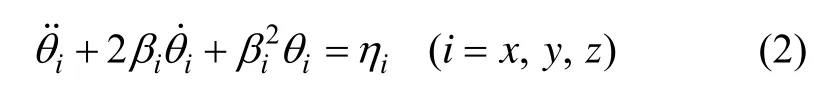
1.2 惯导误差传播模型

舰机传递对准过程中，涉及到主、子两套惯性导航系统，其误差传播特性同单个惯导系统的误差传播特性有一定差异。在进行传递对准建模处理过程中，需要对惯导系统误差传播模型中的相关参量进行重新定义和处理，以区别于研究单个惯导时的情形。

定义舰体主惯导的体坐标系为a系，载机子惯导的体坐标系定义为b系，主惯导的导航坐标系记为n系，子惯导的导航坐标系记为n′系；定义捷联惯导的计算导航坐标系（数学平台）同实际导航坐标系对应坐标轴之间的误差角为姿态失准角，记为。则地理坐标系内，捷联惯导系统的误差传播模型为[11]：

1.3 传递对准模型

1.3.1 状态方程

取状态向量为：

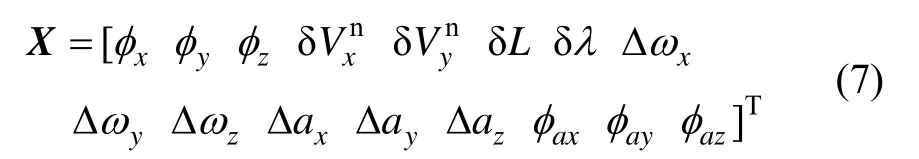
式中：各分量依次分别为姿态失准角、主子惯导东向及北向速度之差、经纬度之差、子惯导的陀螺常值漂移、加速度计测量零偏和变形角。

系统的状态方程为：

式中：A为系统状态转移矩阵；B为系统过程噪声驱动矩阵；W为系统过程噪声向量。A、B中各量由前文给出的惯导系统误差传播方程确定。

1.3.2 “速度+姿态”观测方程

在采用“速度+姿态”匹配模式时，系统的观测向量为

观测方程为：

舰载机着舰后在甲板上停放的位置是随机的，利用着舰后机载惯导关机时刻的导航信息，能够得到下次值机起飞前舰载机相对舰船基准粗略的姿态关系。

2 舰机传递对准自适应滤波方法

2.1 可观测度分析

为了动态调节卡尔曼滤波器各分量通道增益，利用可观测性矩阵的奇异值分解法（Singular Value Decomposition，简称 SVD法）对系统状态分量的可观测性进行定量分析。该方法根据齐次系统模型的系数矩阵构造可观测性矩阵，然后求取可观测性矩阵的奇异值，根据其大小判断状态分量的可观测程度。

对于以惯性导航误差参数建立的状态方程来说，可以运用分段线性定常系统（Piece-Wise Constant System，简称PWCS）来讨论系统的可观测性。为了简化分析，减少计算量，利用系统的提取可观测性矩阵（Stripped Observability Matrix，简称SOM）来替代完全可观测性矩阵（Total Observability Matrix，简称TOM）。根据系统的状态方程式(8)和观测方程式(10)，得到系统SOM矩阵为：

式中：n为状态向量维数，G为系统的可观测性矩阵。利用奇异值分解法，G可表示为：

式中：Z为系统的观测值，X0为初始状态。

当观测量Z具有常值范数时，待估计的初始状态X0形成一个椭球，其方程为：

因此，奇异值越大，椭球半径越小，对初始状态的估计性能越好，即好的估计值对应大的奇异值。状态分量的可观测度定义为：

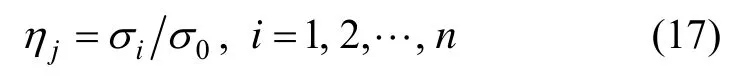
2.2 状态参数分组

从可观测性角度来说，惯导传递对准状态参数可分为观测性好、观测性差以及不可观测三类。在滤波器估计子惯导导航参数误差的同时，采用SVD方法对系统各状态分量进行可观测度计算，从数值上看，以上三类状态分量可观测度的数值大小存在较大差异，在构造自适应衰减因子前，首先按可观测度大小对各状态分量进行分组。

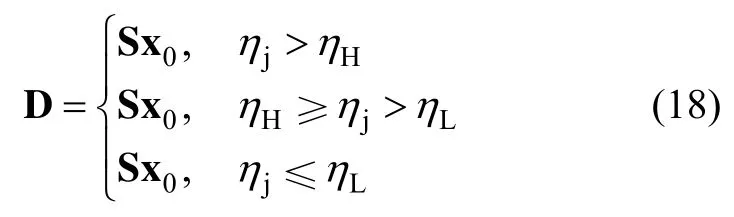
在进行集合划分时，要求各子集之间互不相交。经上述筛选处理后，Sx(n)中所有状态分量按可观测度数值大小划分到高-中-低（Sx0、Sx1和Sx2）三个子集中。

2.3 自适应调节滤波算法

为了抑制可观测度差的分量通道引起的滤波精度下降，根据各状态分量可观测度大小权重，在卡尔曼滤波器增益矩阵Kk各行增加一个衰减因子Γj，以减小不良数据通道对整个滤波器的影响，提高滤波算法估计精度，下面给出自适应调节衰减因子的构造方法。

第一步：根据式(18)的分组结果构造各组衰减因子的基准，此基准为各子集中状态分量可观测度的极大值，用mμ表示：

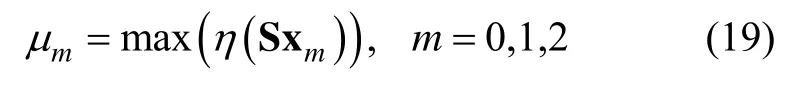
式中：m为子集序列号，表示子集Sxm中各状态分量的可观测度；

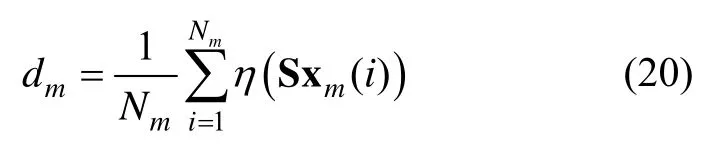
式中：Nm为子集Sxm中状态分量的个数。

第三步：利用式(19)、式(20)构造衰减因子Γj：

至此，自适应衰减因子构造完毕。卡尔曼滤波器当前时间段的增益矩阵为，将衰减因子Γj乘到Kk的第j行各元素上，即得到衰减后的增益矩阵：

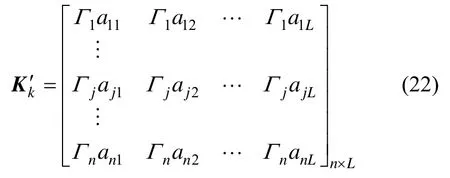
式中：axy为矩阵Kk中的元素。

卡尔曼滤波器的状态估计方程变为：

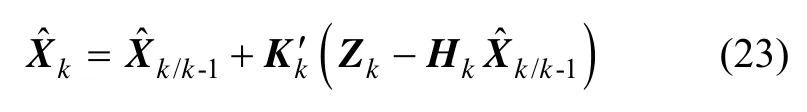
3 仿真分析

3.1 仿真条件

以“速度+姿态”匹配模式为例，采用模拟轨迹分别对基于常规卡尔曼滤波和自适应调节滤波的舰机传递对准进行仿真对比分析。

在二级海情下，舰船以10 m/s的速度做匀速直线运动，仿真时间15 min；主惯导陀螺常值漂移0.0012 (°)/h(1σ)，加表零偏 6×10-6g(1σ)；子惯导陀螺常值漂移0.06 (°)/h(1σ)，加表零偏3×10-4g(1σ)；主、子惯组数据更新周期为0.1 s，传递对准滤波周期为0.2 s；舰体坐标系内横向、法向和纵向杆臂为[2 m 6.7 m 35 m]，预设安装误差角和甲板静态变形角之和为1.0°。

3.2 仿真结果

3.2.1 可观测度分析结果

对舰机传递对准滤波估计进行可观测度分析，根据PWCS理论分段计算式(17)中各状态分量可观测度计算方法，模拟轨迹下传递对准可观测度计算结果如表1所示（选取其中一段）。

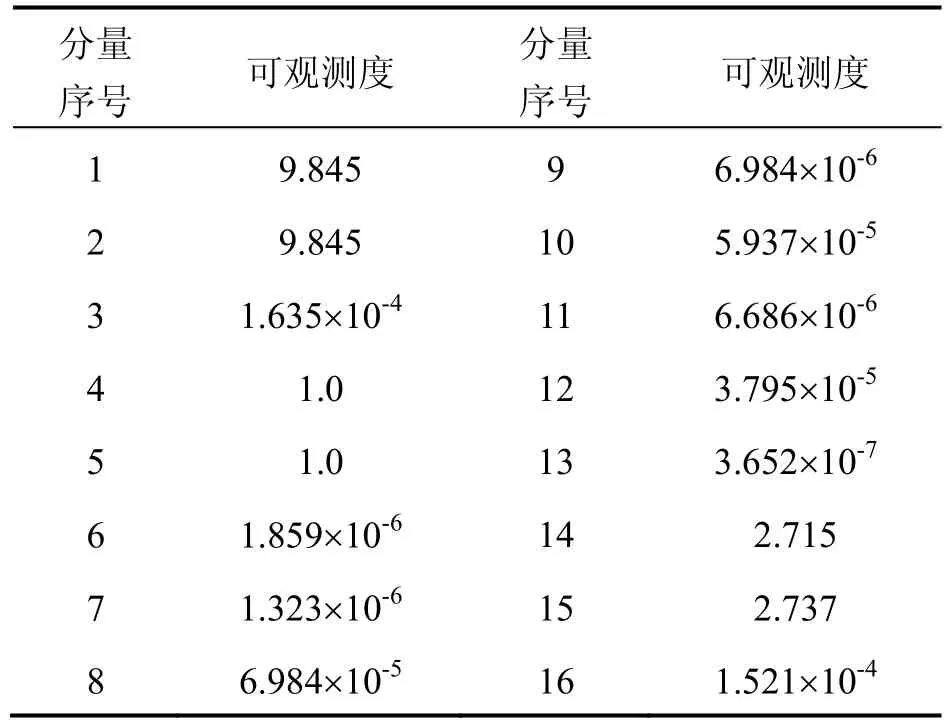
表1 模拟轨迹下状态参数可观测度Tab.1 Observable degree of state parameters under simulation trajectory

3.2.2 模拟轨迹下对准结果

采用舰船模拟轨迹，基于常规卡尔曼滤波和自适应调节滤波的惯导传递对准结果如图1和图2所示。

两种传递对准方法的滤波估计精度对比如表2所示，表中Δφ为姿态失准角估计误差，为变形角估计误差。

图1 姿态失准角估计误差Fig.1 Estimation error of misalignment angles under simulation trajectory

图2 变形角估计误差Fig.2 Estimation error of deformation angles under simulation trajectory

表2 仿真结果对比Tab.2 Comparison of simulation results

3.3 仿真分析

由仿真结果图1、图2和表2可以看出，与基于常规卡尔曼滤波的传递对准相比，采用自适应调节滤波方法时，能够减小三向姿态失准角和变形角的估计误差，对准精度由3′提高到2′，并且传递对准时间（滤波估计收敛时间）由15 min缩短至8 min。仿真结果表明自适应调节滤波方法具有较高的精度和较快的收敛速度。

4 结 论

本文建立了地理系下的舰机惯导传递对准模型，给出了可观测度分析方法。针对舰机传递对准的特点，对常规卡尔曼滤波方法进行了改造，提出了基于状态参数可观测度分析的舰机传递对准自适应滤波方法。舰船模拟轨迹下的仿真对比分析表明，本文提出的自适应传递对准方法可有效地提高舰机传递对准精度，缩短滤波收敛时间，满足舰载机惯导快速高精度初始对准的需求。

[1]Liu Xin,Wang Bo,Deng Zhihong,et al.C[C]//International Conference on Mechanical Engineering and Materials.Melbourne,Australia,2012:1155-1158.

[2]朱蕾，袁书明，陈晶.舰船平台上一种改进的传递对准方案设计与仿真[J].中国惯性技术学报，2010，18(1)：58-62.ZHU Lei,YUAN Shu-ming,CHEN Jing.Improved approach and simulation of shipboard transfer alignment [J].Journal of Chinese Inertial Technology,2010,18(1):58-62.

[3]Yang Dongfang,Wang Shicheng,Li Hongbo,et al.Performance enhancement of large-ship transfer alignment:a moving horizon approach[J].Journal of Navigation,2013,66(1):17-33.

[4]王司，邓正隆.惯导系统动基座对准技术综述[J].中国惯性技术学报，2003，11(2)：61- 67.WANG Si,DENG Zheng-long.Technique review of transfer alignment of inertial navigation system on moving Base[J].Journal of Chinese Inertial Technology,2003,11(2):61-67.

[5]Dai Hongde,Zhou Shaolei，Xu Qinjiu,et al.Comparison of three rapid transfer alignment algorithms[C]//International Conference on Materials Science and Information Technology.Singapore,2012:3483-3488.

[6]陈雨，赵剡，李群生.一种可观测度分析方法及在传递对准中的应用[J].中国惯性技术学报，2013，21(4)：467-471.CHEN Yu,ZHAO Yan,LI Qun-sheng.Observable degree analysis method and its application in transfer alignment [J].Journal of Chinese Inertial Technology,2013,21(4):467-471.

[7]杨晓霞，阴玉梅.可观测度的探讨及其在捷联惯导系统可观测性分析中的应用[J].中国惯性技术学报，2012，20(4)：406-409.YANG Xiao-xia,YIN Yu-mei.Discussions on observability and its applications in SINS[J].Journal of Chinese Inertial Technology,2012,20(4):406-409.

[8]Long Rui,Qin Yongyuan,Jia Jichao.Observable degree analysis of SINS initial alignment based on singular value decomposition[C]//IEEE International Symposium on Knowledge Acquisition and Modeling Workshop.Wuhan,China,2008:444-448.

[9]Pehlivanoglu A G,Ercan Y.Investigation of flexure effect on transfer alignment performance[J].Journal of Navigation,2013,66(1):1-15.

[10]Wu Wei,Chen Sheng,Qin Shiqiao.Online estimation of ship dynamic flexure model parameters for transfer alignment[J].IEEE Transactions on Control Systems Technology,2013,21(5):1666-1678.

[11]韩鹏鑫，穆荣军，崔乃刚.两种坐标系下惯导传递对准效果比较[J].中国惯性技术学报，2010，18(3)：272-278.HAN Peng-xin,MU Rong-jun,CUI Nai-gang.Comparison between transfer alignments of inertial navigation system in two coordinates[J].Journal of Chinese Inertial Technology,2010,18(3):272-278.

Adaptive filtering algorithm based on observable degree analysis of state parameters in carrier-aircraft transfer alignment

LIANG Hao1,WANG Dan-dan2,MU Rong-jun1
(1.Department of Astronautics,Harbin Institute of Technology,Harbin 150001,China;2.China Academy of Launch Vehicle Technology,Beijing 100076,China)

In view of the characteristics of limited maneuver and poor observable degree in carrier-aircraft INS’s transfer alignment,an adaptive filtering algorithm based on observable degree analysis of state parameters is proposed.The state parameters’ observable degree is quantized,and the adaptive factors are constructed based on grouping mechanism.Filtering gain attenuation technique is used to process the variables channels with poor observable degree in order to improve the accuracy and stability of filtering estimation.Simulation results show that the adaptive filtering algorithm has higher precision and faster convergence speed compared to classic methods,which could improve alignment precision to 2′ from 3′ and shorten filtering time to 8 min from 15 min.

carrier-aircraft,transfer alignment,observable degree analysis,filtering gain attenuation

V249.32

：A

1005-6734(2014)01-0058-05

10.13695/j.cnki.12-1222/o3.2014.01.012

2013-10-18；

：2014-01-02

国防基础科研项目（C0320110001）

梁浩（1987—），男，博士研究生，研究方向为初始对准及信息融合。E-mail：liangwangyihao@163.com

联 系 人：穆荣军（1969—），男，副教授，博士生导师。E-mail：murjun@163.com