自适应SDV-UPF算法及其在紧组合中的应用

赵 岩，高社生，杨 一

（西北工业大学 自动化学院，西安 710072）

自适应SDV-UPF算法及其在紧组合中的应用

赵 岩，高社生，杨 一

（西北工业大学 自动化学院，西安 710072）

针对粒子滤波存在重要性密度函数难以选取和系统状态协方差阵可能出现的负定性问题，提出一种新的自适应奇异值分解无迹粒子滤波(ASVD-UPF)算法。该算法采用自适应因子修正动力学模型误差，通过奇异值分解抑制系统状态协方差矩阵的负定性，并以改进的 UKF算法产生重要性密度函数，以弥补粒子滤波的缺陷，使该算法适用于非线性、非高斯系统模型的滤波计算。将提出的算法应用到所设计的GPS/SINS/PL紧组合导航系统中进行仿真验证，结果表明，提出算法的经、纬度误差、速度误差和姿态误差范围分别控制在(-0.5″,+0.5″)、(-0.8 m/s,+0.8 m/s) 和(-1′,+1′)以内，误差估计的精度和收敛速度明显优于UKF和PF算法，能提高组合导航系统的解算精度。

紧组合导航系统；伪距；奇异值分解；无迹粒子滤波

目前，解决非线性系统模型常用的滤波算法主要有扩展卡尔曼滤波(Extended Kalman Filtering,EKF)、无迹卡尔曼滤波(Unscented Kalman Filtering,UKF)和粒子滤波(Particle Filtering,PF)算法。EKF算法的主要思想是对非线性函数进行线性化近似，忽略或逼近高阶项，以解决非线性系统的滤波计算问题。但是，当系统非线性度较严重时，忽略Taylor展开式的高阶项将引起较大的线性化误差，导致 EKF的滤波误差增大甚至发散。其次，Jacobian矩阵的计算量大[1]。为了克服EKF 存在的缺点，Julier[2]提出了基于Unscented变换(UT)的UKF算法，该算法采用确定性采样来近似非线性函数的概率分布，避免了求解Jacobian矩阵计算量大的问题，且对高斯分布的逼近精度可达到三阶[3]。但对于非高斯、强非线性系统模型，滤波精度难以保证。PF通过寻找一组在状态空间中传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态的最小方差估计。PF适用于非线性非高斯系统的状态估计，尤其对强非线性系统的滤波问题有独特的优势，摆脱了解决非线性滤波问题时，随机量必须满足高斯分布的制约条件。但PF存在重要性密度函数难以选取和粒子匮乏等问题[4]。为了解决系统状态协方差阵可能出现的负定性问题和PF的缺陷，文献[1]提出自适应奇异值分解的无迹卡尔曼滤波，将其应用到SINS/SAR组合导航系统中，在一定程度上改善了滤波性能，但由于UKF的局限性，缺乏对非高斯系统的处理能力；文献[5]提出了一种改进的无迹粒子滤波算法。该算法在无迹粒子滤波的采样过程中吸收权值自适应调整的优点，考虑最新量测影响，通过欧氏距离和反映量测噪声统计特性的精度因子来自适应的调整粒子对应权值分布，增加有用粒子的权值，降低粒子退化程度，保持粒子多样性。然而状态协方差阵可能出现的负定性问题。

为了克服上述非线性滤波算法的不足，本文提出一种适合于非线性系统模型的自适应奇异值分解无迹粒子滤波(ASDV-UPF)算法，该算法在充分吸收自适应滤波、奇异值分解和无迹粒子滤波优点的基础上，采用自适应因子修正动力学模型误差，通过奇异值分解抑制系统状态协方差矩阵的负定性，并采用改进的UKF产生重要性密度函数，以弥补PF的缺陷。将提出的ASDV-UPF算法应用到GPS/捷联惯性导航(Strapdown Inertial Navigation System，SINS)/伪卫星(Pseudolites，PL)紧组合系统中进行仿真验证。结果表明，提出的算法适合于非线性动态系统的滤波计算，不但具有良好的数值稳定性和鲁棒性，而且能有效改善滤波性能，提高组合导航的解算精度。

1 ASVD-UPF算法设计

1.1 自适应因子设计

考虑如下非线性系统模型

式中，Xk是状态向量，zk是量测量，f(·)和h(·)是非线性函数；wk和vk分别为系统过程噪声和量测噪声。

预测残差含有未经观测信息修正的状态[6]，更能反映动态系统受到的扰动。因此，以预测残差为变量，构造状态模型的误差判别统计量及自适应因子。预测残差表示为：

用预测残差构造状态模型误差判别统计量：

自适应因子函数选用：

1.2 奇异值分解

1.3 提出的ASVD-UPF算法

ASVD-UPF算法步骤如下：

1）初始化

从先验密度分布函数中抽取l个样本点，使

通过扩维得到：

权值为：

式中，α表示 Sigma点相对均值的扩散程度(通常)，β是关于系统先验信息的参数。对高斯分布，β=2最佳[1]，l为系统状态维数。

2）奇异值分解，计算sigma点集

计算特征点协方差矩阵和2l+1个Sigma点向量：

式(10)中，ρ为缩放比例因数，较为恰当的取值为，σi,k为奇异值分解因子。

3）时间更新

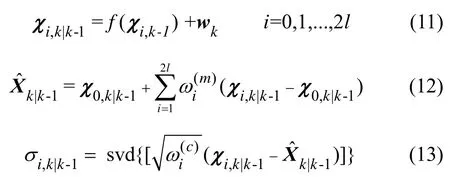
式(13)中，svd{·}为SVD分解算子，

4）量测更新

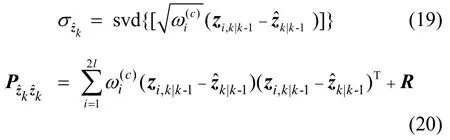
式(16)中的Q与公式(20)中的R分别为系统噪声方差和量测噪声方差。

选择重要性函数为：

5）从建议分布函数中抽取粒子，并进行权值更新与归一化：

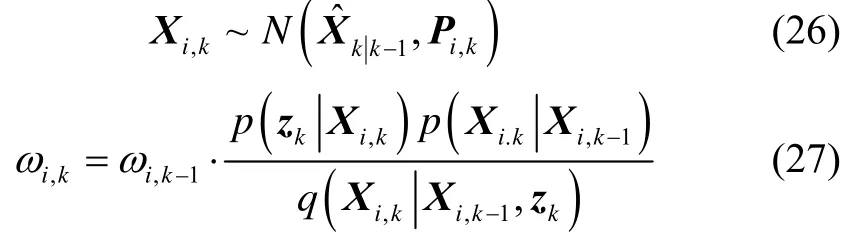
得到归一化权值：

6）重采样

2 GPS/SINS/PL组合导航系统模型

由于GPS提供的位置和速度并非原始量测数据，而是经过数据处理后得到的计算值，因而各量测间存在一定的相关性，这将会影响导航参数解的精确性。而卫星接收机提供的伪距、伪距率信号是接收机接收的原始信息，不需要经过导航解算，且各伪距、伪距率信号的误差独立、互不相关[8]。因此，基于伪距、伪距率的GPS/SINS组合系统不仅便于导航滤波器的设计与实现，而且该方式大大增强了测量方程的可观性。同时在理论上，采用伪距、伪距率组合方式的效果比位置、速度组合方式好[9]。当GPS信号被遮掩、被干扰或者可见星数不足时，用PL代替GPS卫星，形成SINS/PL组合导航系统，可继续保持较高精度完成导航任务。为此本文采用基于伪距/伪距率的GPS/SINS/PL紧组合方式，提高组合导航系统性能。

2.1 组合系统的状态方程

在东北天坐标系中，组合系统的状态量选取为

式中，δL,δλ,δh为位置误差，为速度误差，为姿态误差，为陀螺随机漂移，为陀螺一阶马尔科夫过程，为加计零偏，δtu和δtru分别为由时钟误差引起的等效距离误差和时钟误差频率引起的等效距离率误差。状态量存在如下非线性关系：

式中，Cω欧拉平台误差角矩阵，分别为导航坐标系(n系)至计算坐标系(c系)的姿态变换矩阵和机体坐标系(b系)至c系的，为地球自转角速度实际值和理想值，理想陀螺角速度输出，为 n系至地心惯性坐标系(i系)的角速度，分别为n系至地球坐标系(e系)的角速度实际值和理想值，分别为的计算误差，实际加速度计比力输出和加速度计测量误差，为实际速度和速度误差，δg重力加速度误差，L和h为纬度和高度、为当地子午圈和卯酉圈曲率半径，式(32)中各参数的关系推导参考文献[10]。

组合系统的状态方程为：

式中，f(·)为连续非线性函数，由式(32)给出，W(t)为状态噪声。

2.2 组合系统量测方程

设SINS在ECEF坐标系中位置为(x,y,z)，则式(34)在(x,y,z)处泰勒展开为：

式中，

GPS(或PL)接收机相对于第i颗卫星测得的伪距为

SINS与第i颗卫星之间的伪距率为：

GPS(或 PL)接收机相对于第i颗卫星测得的伪距率为：

组合系统的量测量和量测方程分别为

式(41)中，h(·)为连续非线性函数，V(t)为量测噪声。

3 仿真实验与分析

3.1 仿真初始条件

假设无人机初始位置为东经108.997°，北纬34.246°，高度1000 m，飞艇以20 m/s的速度匀速向北飞行。仿真时间为1000 s，SINS的采样周期为0.01 s，GPS的采样周期为1 s，滤波周期为1 s。其他仿真参数如表1所示。

表1 仿真初始条件Tab.1 Initial conditions of simulation

3.2 结果分析

将现有的UKF、PF和本文设计的ASVD-UPF算法应用到所设计的基于伪距/伪距率的GPS/SINS/PL紧组合导航系统中，进行仿真实验，结果如图1～3所示。

图1是组合导航系统经度、纬度和高度误差曲线，可以看出，采用UKF和PF算法所获得的滤波精度基本相当，经度和纬度误差稳定在(-1.2″,+1.2″)，UKF算法的高度误差稳定在(-5 m,+7 m)，PF算法的高度误差稳定在(-5 m,+3 m)；采用设计的ASVD-UPF算法获得的位置误差更小，经度、纬度和高度误差范围分别控制在(-0.5″,+0.5″)、(-0.5″,+0.5″)和(-2 m,+2 m)，而且收敛速度更快。

图2是组合导航系统速度误差曲线，通过 UKF计算得到的速度误差范围在(-2 m/s,+2 m/s)；由PF得到的速度误差控制在(-1.5 m/s,+1.5 m/s)；而本文设计的算法得到速度误差为(-0.8 m/s,+0.8 m/s)。设计的ASVD-UPF算法对于速度误差的估计精度要高于UKF和PF算法的估计精度。

图3是组合导航系统姿态误差曲线，通过UKF计算得到的三个方向的姿态误差范围分别为(-1′,+1′)、(-1′,+1′)和(-2′,+2′)；由PF得到的三个方向的姿态误差范围分别为(-1′,+1′)、(-1′,+1′)和(-1.5′,+1.5′)；而本文设计的算法得到三个方向的姿态误差范围分别为(-0.5′,+0.5′)、(-0.5′,+0.5′)和(-1′,+1′)。设计的ASVD-UPF算法对于姿态误差的估精度也高于 UKF和PF算法的估计精度，不仅反映出设计ASVD-UPF算法对姿态误差估计精度的优越性，而且，从仿真图对比可以看出，采用 ASVD-UPF算法的航向角误差的收敛速度更快。

图1 三种算法输出的位置误差曲线Fig.1 Position errors of the three filtering methods

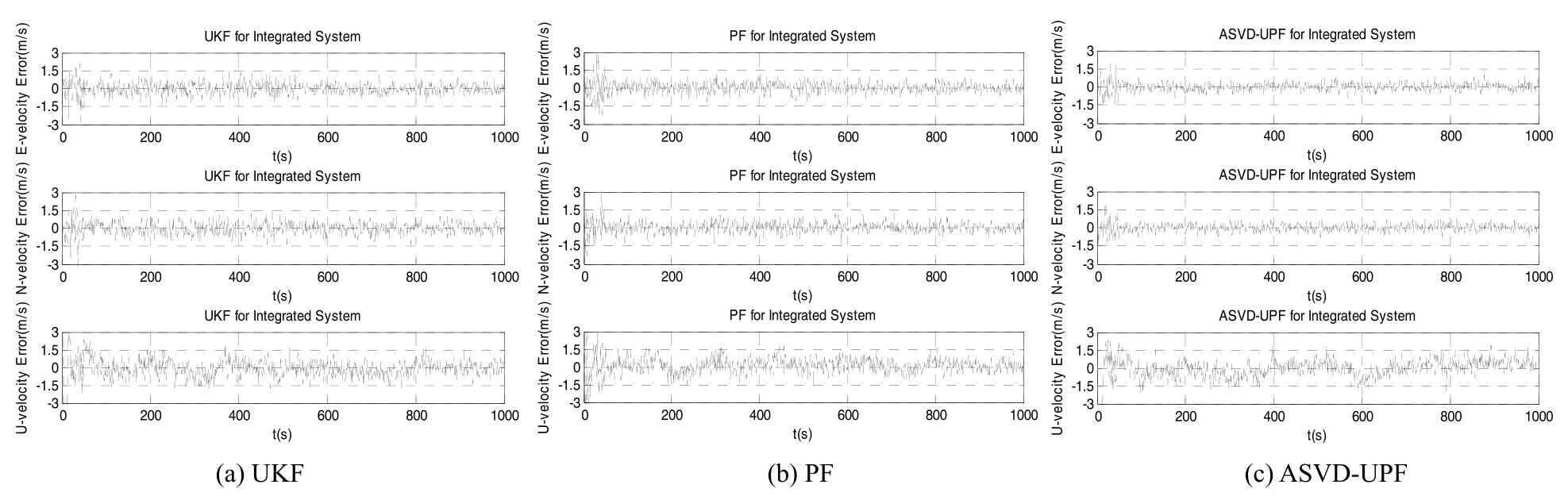
图2 三种算法输出的速度误差曲线Fig.2 Velocity errors of the three filtering methods

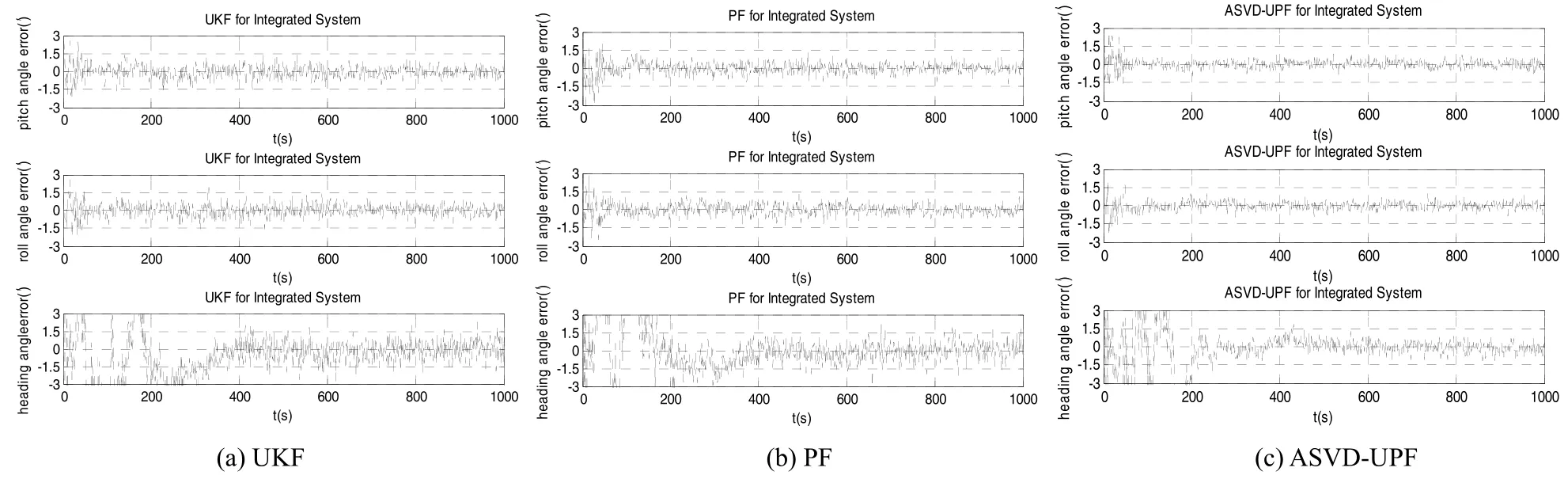
图3 三种算法输出的姿态误差曲线Fig.3 Attitude errors of the three filtering methods

4 结 论

采用 PL辅助 GPS，设计了基于伪距/伪距率的GPS/SINS/PL紧组合导航系统，以克服GPS信号被遮挡、被干扰或是可见星数不足时导致导航精度下降的缺陷，并提出自适应奇异值分解无迹粒子滤波(ASDV-UPF)算法。该算法充分吸收自适应滤波、奇异值分解和无迹粒子滤波的优点，采用自适应因子修正动力学模型误差，通过奇异值分解抑制系统状态协方差矩阵的负定性，并采用改进的UKF产生重要性密度函数，以弥补PF的缺陷。通过仿真实验验证了设计的ASVD-UPF算法在误差估计精度和收敛速度明显优于UKF和PF算法，提高了非线性导航系统的导航定位精度。

（References）：

[1]高社生，王建超，焦雅林.自适应SVD-UKF算法及在组合导航的应用[J].中国惯性技术学报，2010，18(6)：737-741，765.GAO She-sheng,WANG Jian-chao,JIAO Ya-lin.Adaptive SVD-UKF algorithm and application to integrated navigation[J].Journal of Chinese Inertial Technology,2010,18(6):737-741,765.

[2]Julier S J,Uhlmann J K.Unscented filtering and nonlinear estimation[J].Proceedings of the IEEE,2004,92(3):401-422.

[3]Julier S J,Laviola J J.On Kalman filtering with nonlinear equality constranits[J].IEEE Transactions on Signal Processing,2007,55(6):2774-2784.

[4]高社生，阎海峰，高怡.模糊抗差自适应粒子滤波及其在组合导航中的应用[J].中国惯性技术学报，2010，18(5)：561-566.GAO She-sheng,YAN Hai-feng,GAO Yi.Fuzzy robust adaptively particle filter method and application to integrated navigation system[J].Journal of Chinese Inertial Technology,2010,18(5):561-566.

[5]薛丽，高社生，赵岩.权值自适应调整Unscented粒子滤波及其在组合导航中的应用[J].中国惯性技术学报，2012，20(4)：459-463.XUE Li,GAO She-sheng,ZHAO Yan.Unscented particle filtering with adaptive adjusted weight and its application in integrated navigation[J].Journal of Chinese Inertial Technology,2012,20 (4):459-463.

[6]GAO She-sheng,GAO Yi,ZHONG Yong-min,et al.Random weighting estimation method for dynamic navigation positioning[J].Chinese Journal of Aeronautics.2011,24:318-323.

[7]GAO She-sheng,ZHONG Yong-min,LI Wei.Robust adaptive filtering method for SINS/SAR integrated navigation system[J].Aerospace Science and Technology.2011,15:425-430.

[8]GUO Zhen,HAO Yanling,SUN Feng,et al.Sigma-point Kalman filtering for tightly-coupled GPS/INS[C]//IEEE International Symposium on Knowledge Acquisition and Modeling Workshop.2008:844-847.

[9]NIE Qi,GAO Xiao-ying.Comparison of nonlinear filtering approach in tightly-coupled GPS/INS navigation system[C]//2012 10th World Congress on Intelligent Control and Automation.2012:1176-1181.

[10]严恭敏，严卫生，许德民.基于欧拉平台误差角的SINS非线性误差模型研究[J].西北工业大学学报，2009，27(4)：511-516.YAN Gong-min,YAN Wei-sheng,XU De-min.A SINS nonlinear error model reflecting better characteristics of SINS errors[J].Journal of Northwestern Polytechnical University,2009,27(4):511-516.

Adaptive SVD-UPF algorithm and application to tightly-coupled integrated navigation

ZHAO Yan,GAO She-sheng,YANG Yi
(School of Automation,Northwester Polytechnical University,Xi’an 710072,China)

In view that the importance density function in particle filter is hard to select and the system state covariance matrix is negative definiteness,a new adaptive unscented particle filter based on singular value decomposition (ASVD-UPF) was proposed.The new algorithm is capable of correcting dynamic model error by adaptive factor and restraining the negative definiteness of system state covariance matrix by SVD as well as generating the importance density function to offset defects of PF.With the above advantages,the proposed algorithm is suitable to be applied to the filter calculation of nonlinear and non-Gaussian system model.The proposed algorithm was applied to the GPS/SINS/PL tightly-coupled integrated navigation system and the simulation test was made.The simulation results show that the errors of longitude,latitude,velocity and attitude could be controlled to under (-0.5″,+0.5″),(-0.8 m/s,+0.8 m/s) and (-1′,+1′) respectively by the proposed algorithm.It is proved that the error estimation precision and convergence speed of the proposed algorithm are better than that of UKF and PF,and the positioning precision of integrated navigation is improved.

tightly-coupled integrated navigation;pseudorange;singular value decomposition;unscented particle filter

U666.1

：A

1005-6734(2014)01-0083-06

10.13695/j.cnki.12-1222/o3.2014.01.017

2013-07-06；

：2013-11-01

国家自然科学基金（基金号61174193）；陕西省自然科学基金（基金号NBYU0004）；航天科技创新基金（基金号CASC201102）

赵岩（1983—），男，博士研究生，从事组合导航研究。E-mail：zytyler@163.com

联 系 人：高社生（1956—），男，教授，博士生导师。E-mail：gshshnpu@163.com