与其导数具有分担值的亚纯函数唯一性

陶毅翔

(宁德师范学院数学系,福建宁德352100)

与其导数具有分担值的亚纯函数唯一性

陶毅翔

(宁德师范学院数学系,福建宁德352100)

为进一步丰富亚纯函数唯一性理论,寻求更佳的唯一性条件,利用亚纯函数Nevanlinna理论更精确地估计亚纯函数的n重值点的计数函数,得到两个亚纯函数与其导数具有某些分担值时的唯一性定理,推广和改进了相关文献的相关结果.

亚纯函数;分担值;唯一性

1 引言及主要结果

本文中,采用亚纯函数的Nevanlinna理论的标准记号[1].使用S(r,f)表示任意满足S(r,f)=o{T(r,f)}的量,可能除去r的一个线性测度有穷的集合,且它每次出现并不一定相同,设f(z)与g(z)为两个非常数亚纯函数,k为正整数,a为任意复数,如果f(z)−a与g(z)−a在计重数(不计重数)之下具有相同的零点,则称f(z)与g(z)分担a CM(IM),或者称a为f(z)与g(z)的CM(IM)公共值.Ek(a,f)表示f(z)−a的所有k重(重级零点按其重数计算)零点的集合.Ek)(a,f)表示f(z)−a的m(≤k)重(重级零点按其重数计算)零点集合,即

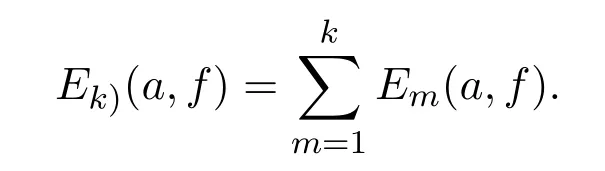
E(k(a,f)表示f(z)−a的n(≥k)重零点的集合.Ek(a,f)=Ek(a,g)表示f(z)−a的k重零点当且仅当是g(z)−a的k重零点.若Ek)(a,f)=Ek)(a,g),则称f(z)与g(z)以k截断分担复数a.

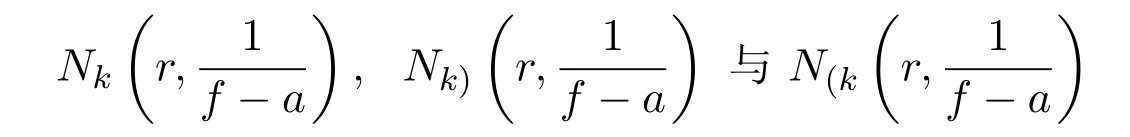
分别表示相应于集合Ek(a,f)、Ek)(a,f)

与E(k(a,f)的计数函数;于是,

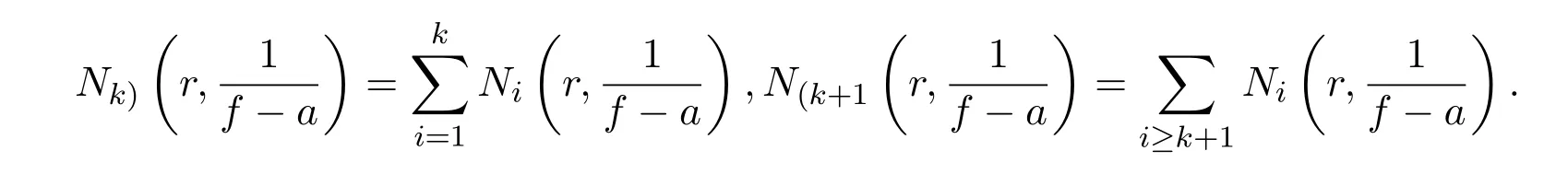
对于亚纯函数与其导数具有公共值时的唯一性问题,1977年,文献[2]证明了:

定理A[2]设f是一个非常数亚纯函数,a,b为两个判别有穷复数,如果E(a,f)=E(a,f′), E(b,f)=E(b,f′),则f≡f′.

1980年,文献[3]证明了:

定理B[3]设f是一个非常数亚纯函数,若对于三个判别的有穷复数a1,a2,a3,有

1986年,仪洪勋应用杨乐方法,改进了Gopalakrishna-Bhoosnurmath的相关结果,证明了下述:

定理C[4]设f与g为非常数亚纯函数,aj(j=1,2,···,q)为q个判别的复数,kj(j=1,2,···,q)为正整数或∞,且满足k1≥k2≥···≥kq,如果则f≡g.

其后,文献[5-7]亦进一步研究了亚纯函数与其导数具有公共值时的唯一性问题.

本文从另一个角度考虑上述问题,得到下列结果,推广和改进了定理A与定理B的结果:

定理1设f是一个非常数亚纯函数,若且如果满足下列两种情况之一:

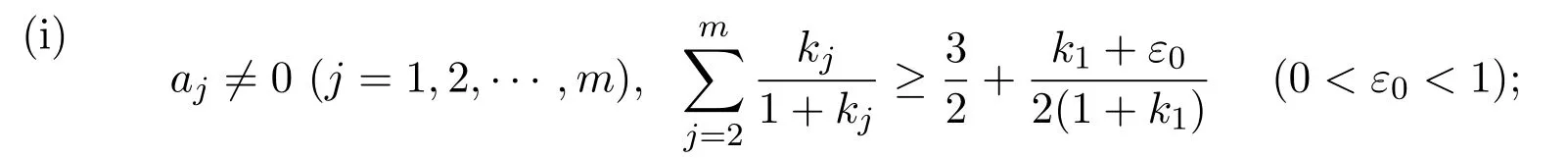
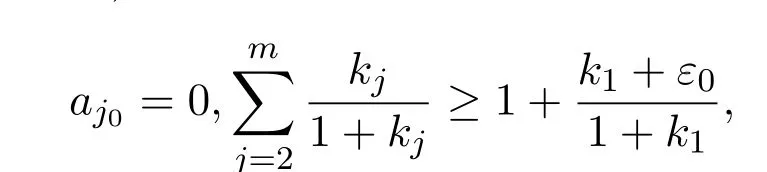
则f≡f′.

定理2设f是一个非常数亚纯函数,若=1,2,···,m,

且k1≥k2≥···≥km,如果满足下列两种情况之一:

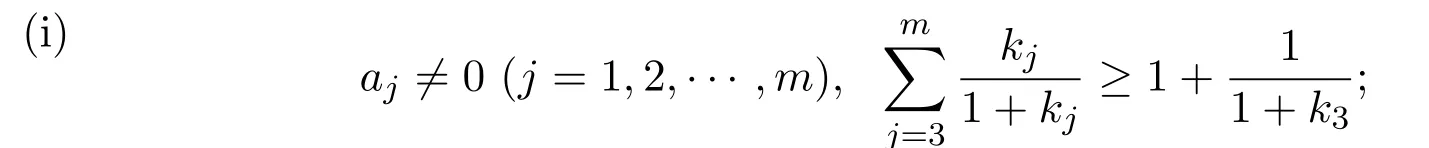
(ii)存在某个j0(1≤j0≤m),使

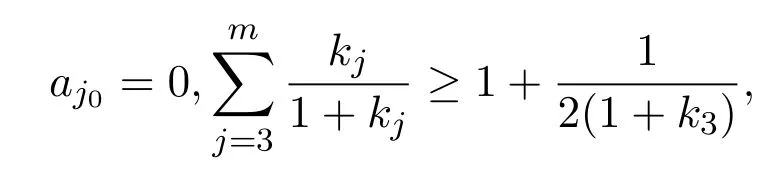
则f≡f′.

2 几个引理

引理1设f是一个非常数亚纯函数,bj(j=1,2,···,m)为互相判别的有穷非零复数,若f̸≡f′且···,m,则

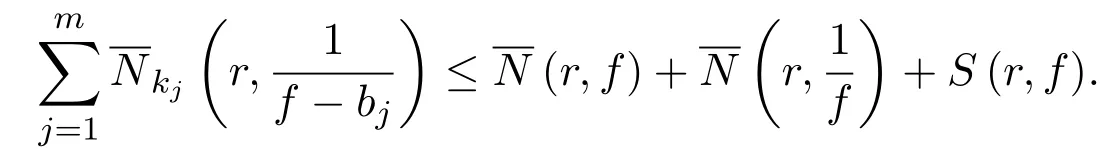
证明设z0为f级零点,由引理的条件知的零点,从而z0为的零点.由于对任意均有因此由此可推知零点.于是由z0的任意性及f̸≡f′,得

引理1得证.

引理2设f为非常数亚纯函数,则

(i)当aj̸=0(j=1,2,···,m)时.有

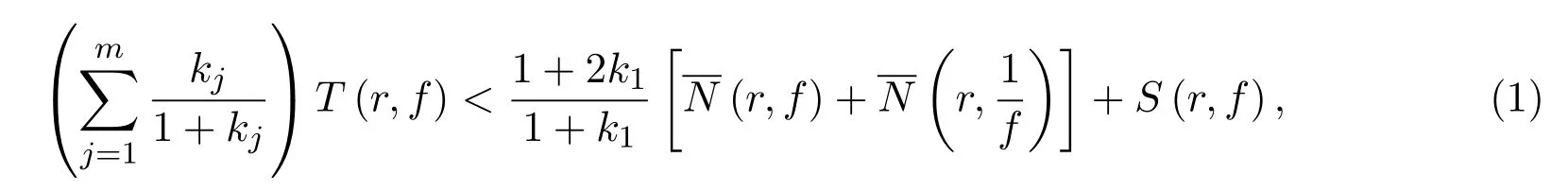
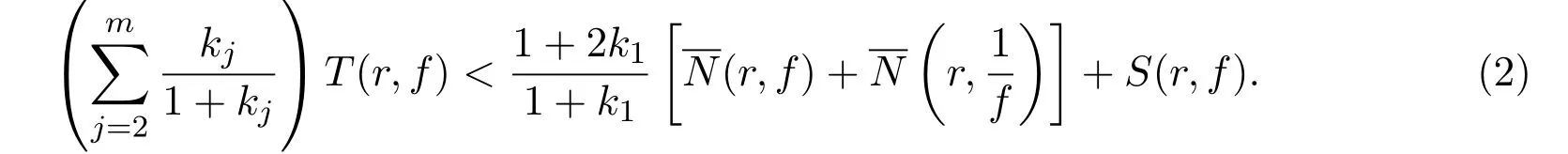
证明(i)由Nevanlinna第二基本定理得:

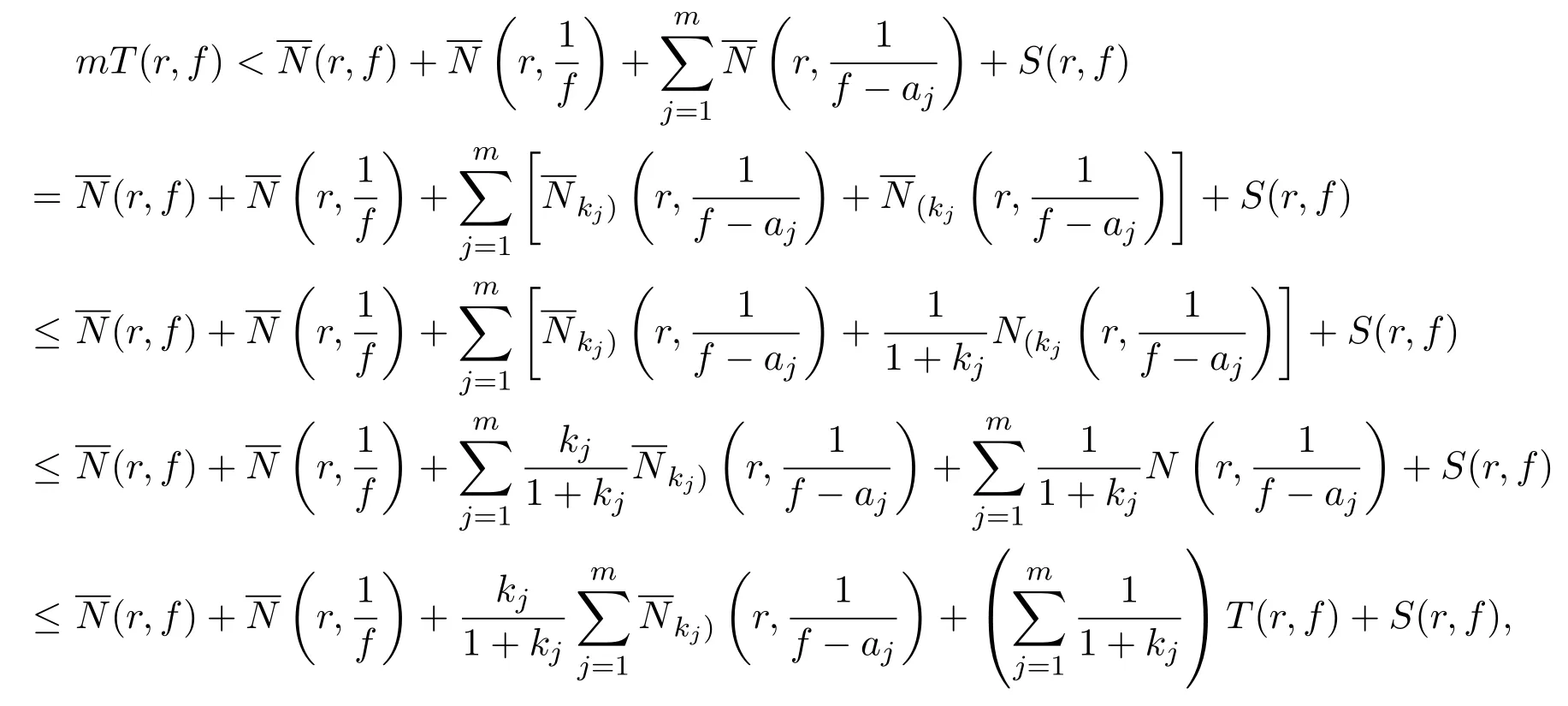
从而由引理1,可得

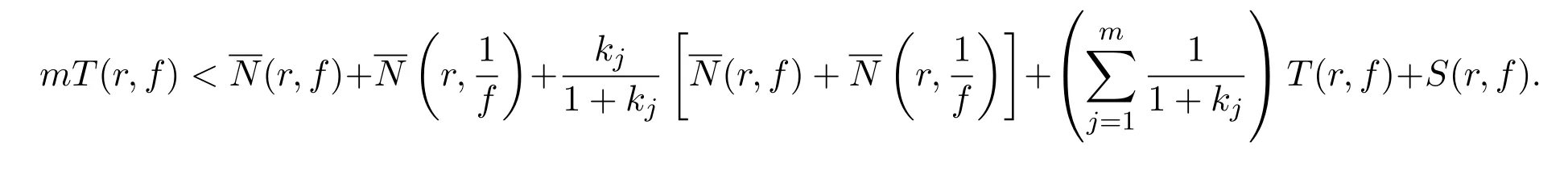
整理后即得(1)式.

其次,由Nevanlinna第二基本定理,得,

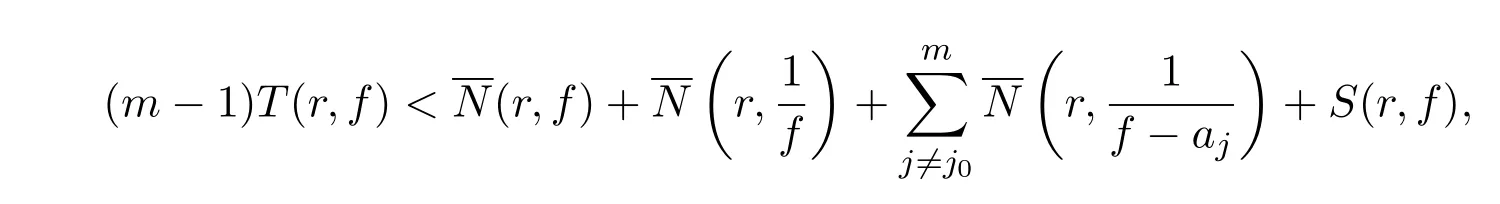
类似于(i)的证明,可得

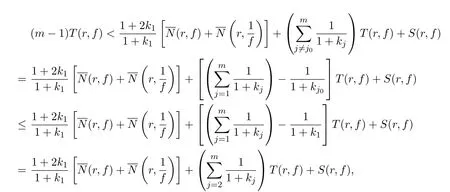
整理后即得(2)式.

综合(i)、(ii)知引理2的结论成立.

引理3设f是非常数亚纯函数,

则

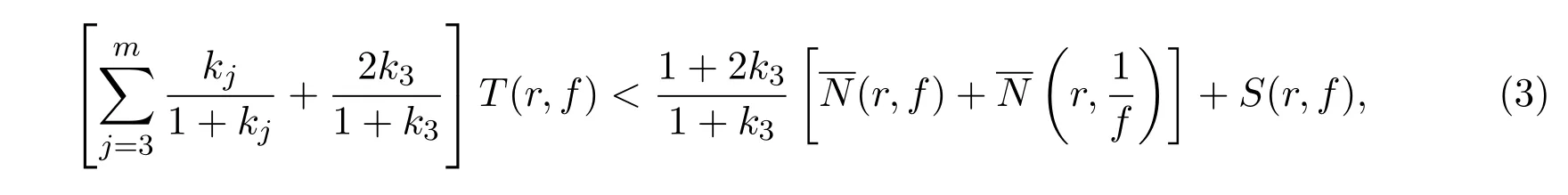
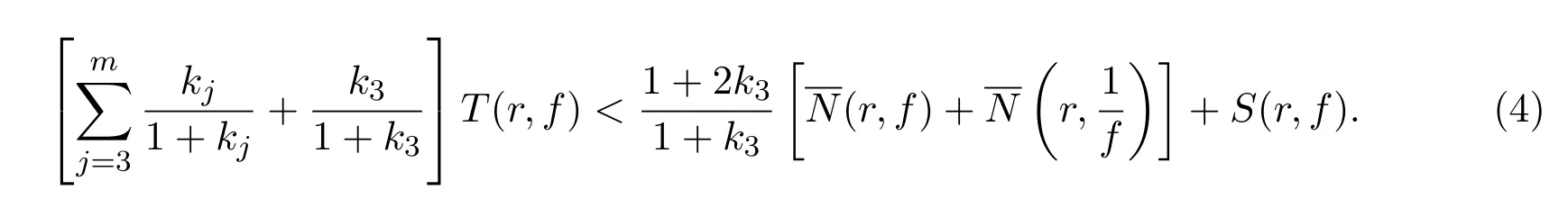
证明(i)由引理2的证明过程可知,有

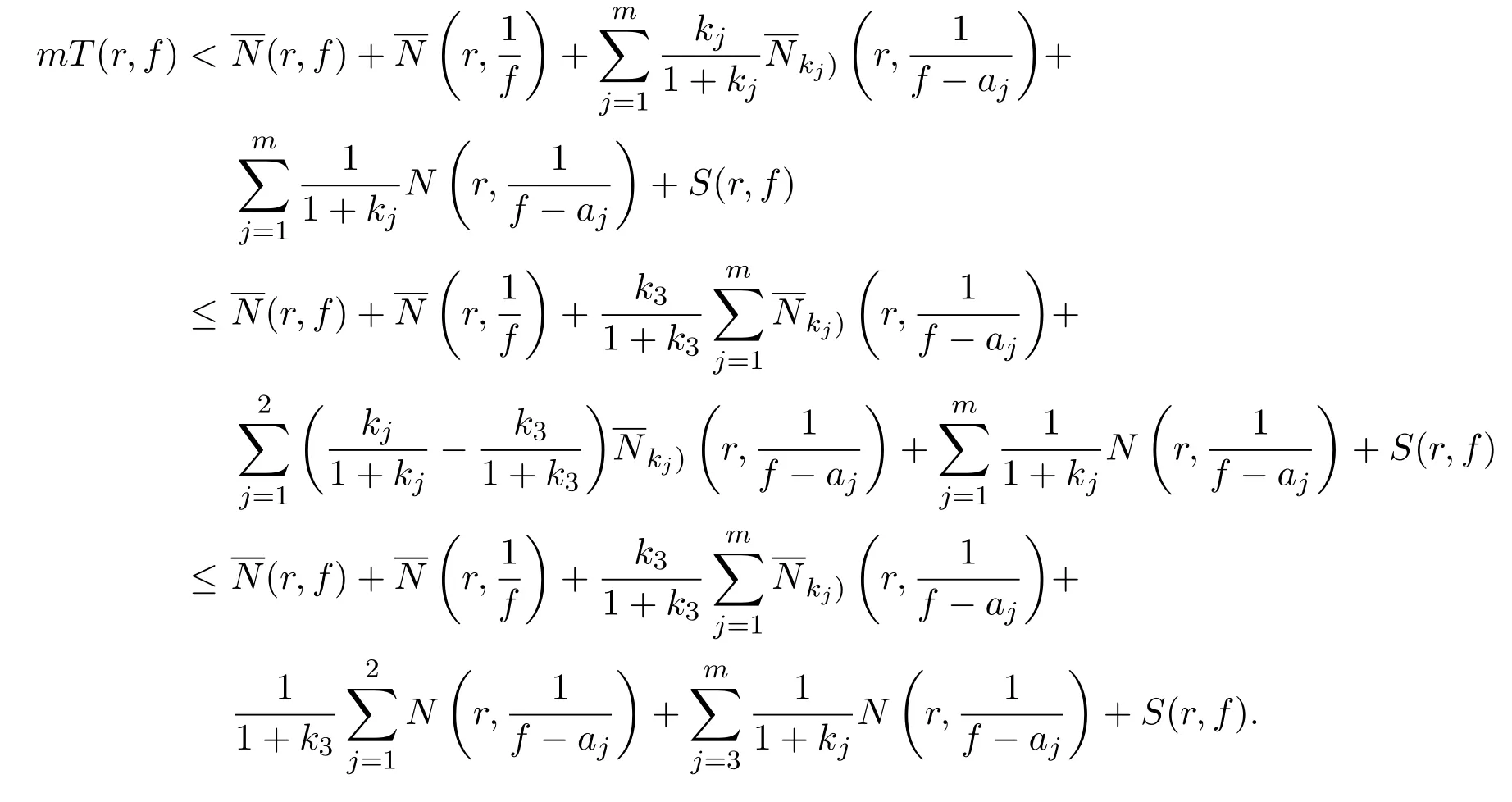
再根据引理1,得

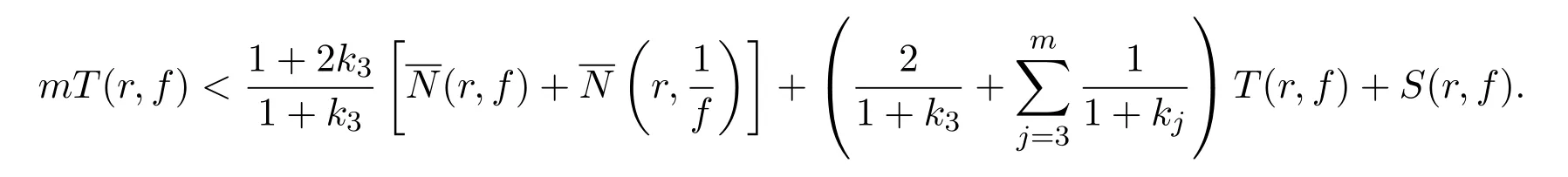
整理后即得(3)式.

(ii)由Nevanlinna第二基本定理及本引理的(i)的证明过程知,有

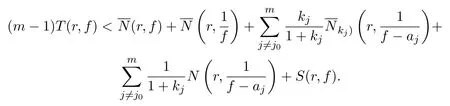
分两种情况证明:

情况Ij0=1或2,则由引理1,得

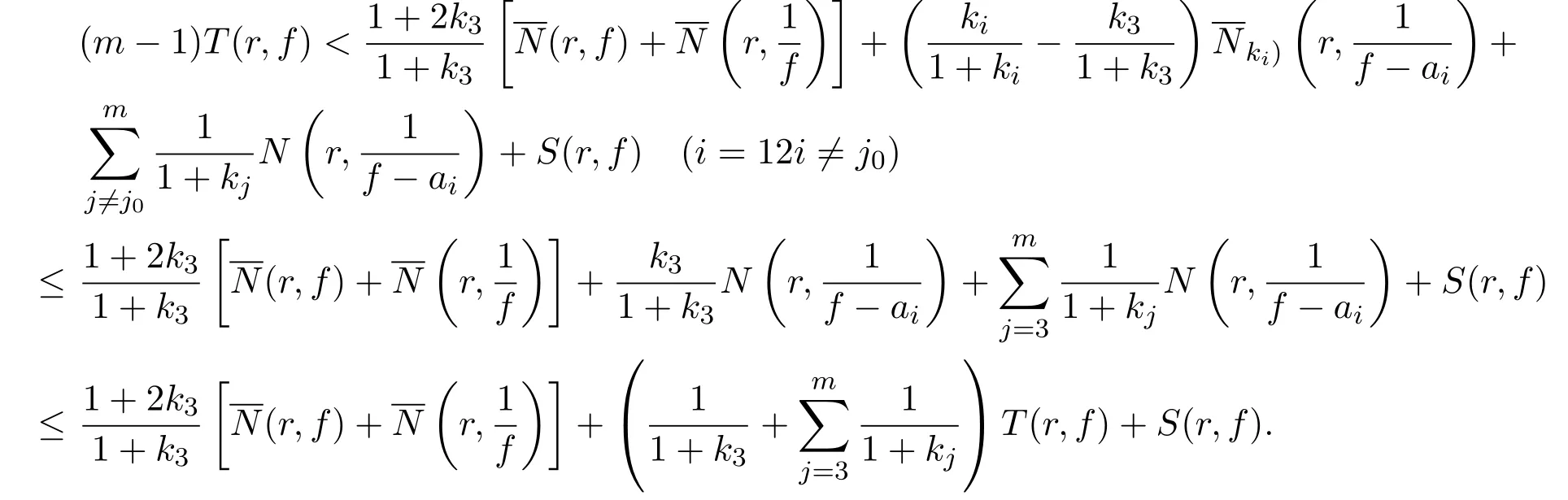
情况IIj0≥3,由引理1,得

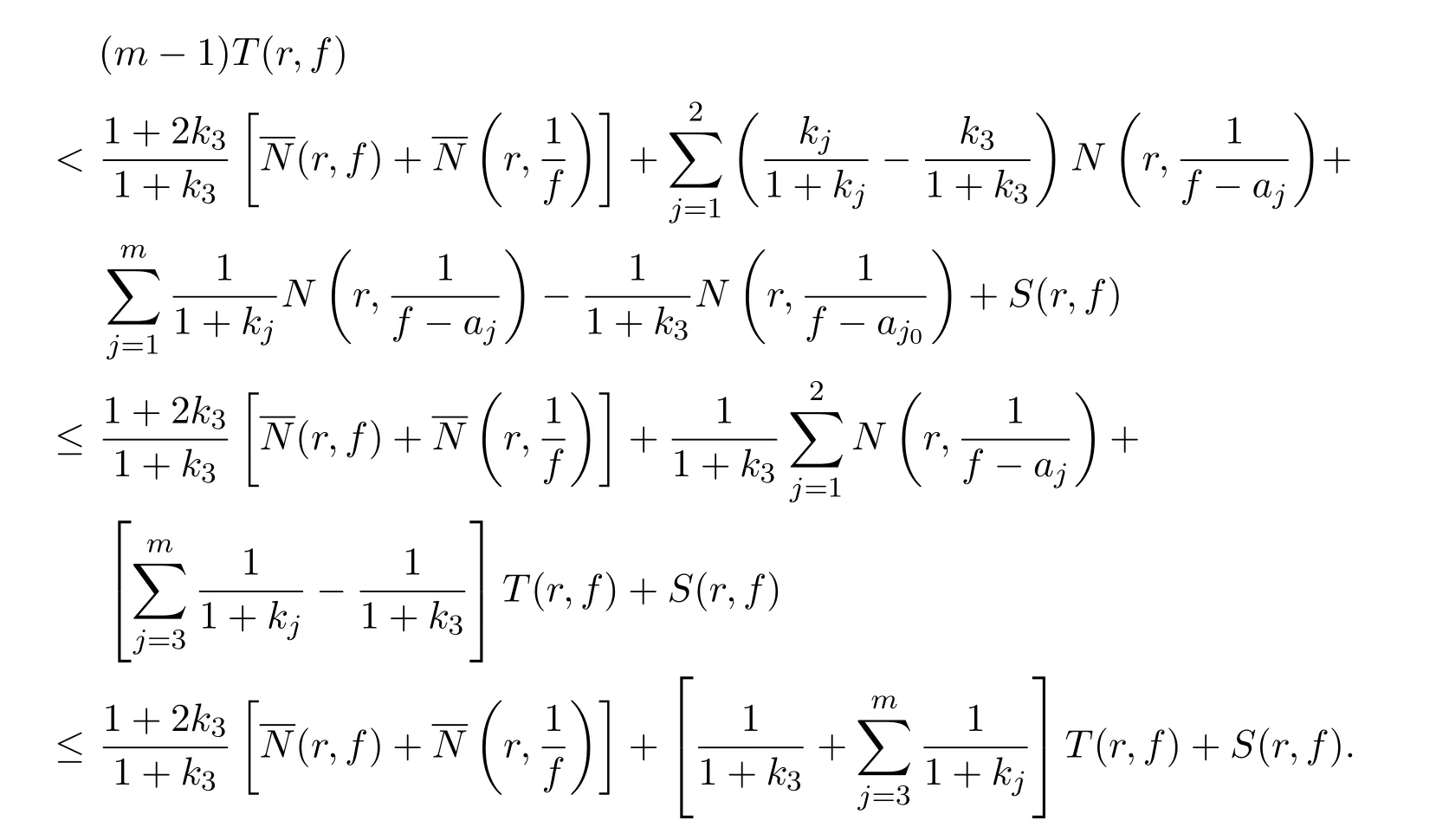
综合情况I和II的讨论知对于1≤j0≤m,均有

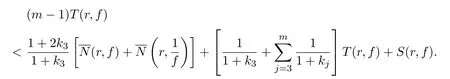
整理后即得(4)式,引理3得证.

3 主要定理的证明

定理1的证明事实上,假定f̸≡f′.若条件(i)满足,则由引理2的(1)式,有

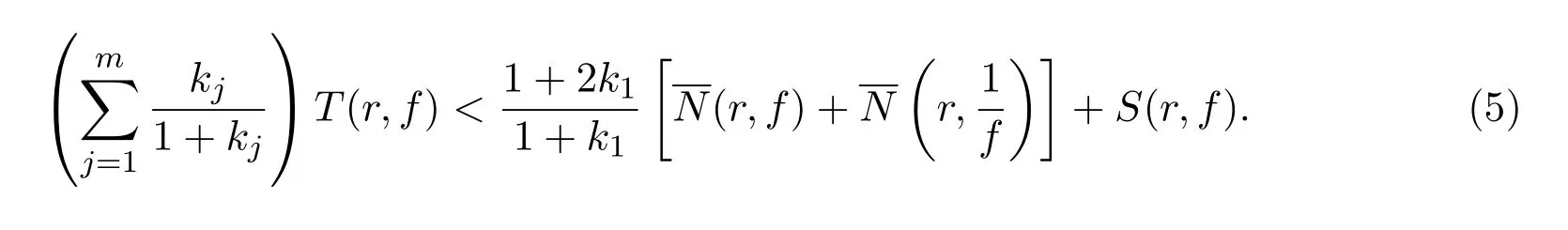
类似于引理2的(i)的证明,易于推得

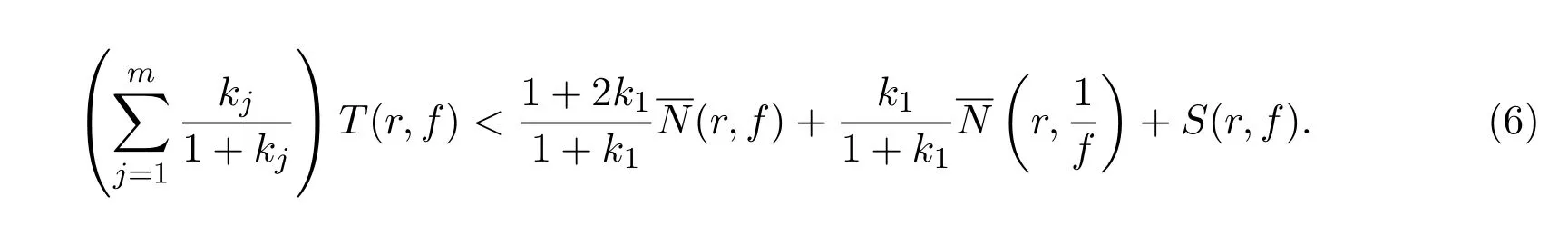
由已知条件

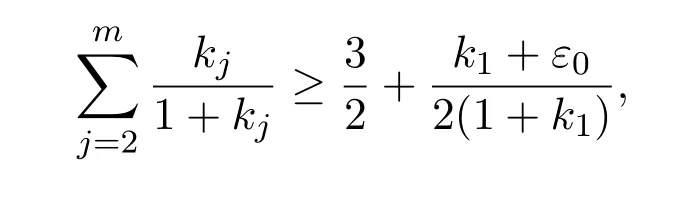
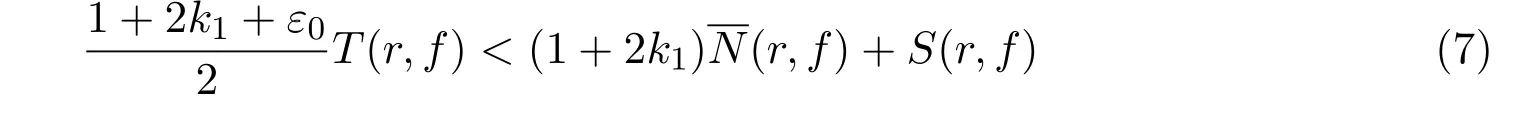
及

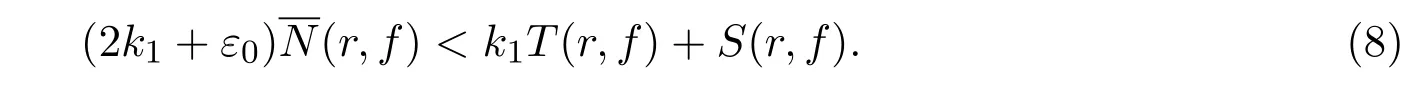
结合(7)、(8)两式即推出矛盾.若条件(ii)满足,则由引理2的(2)式,得

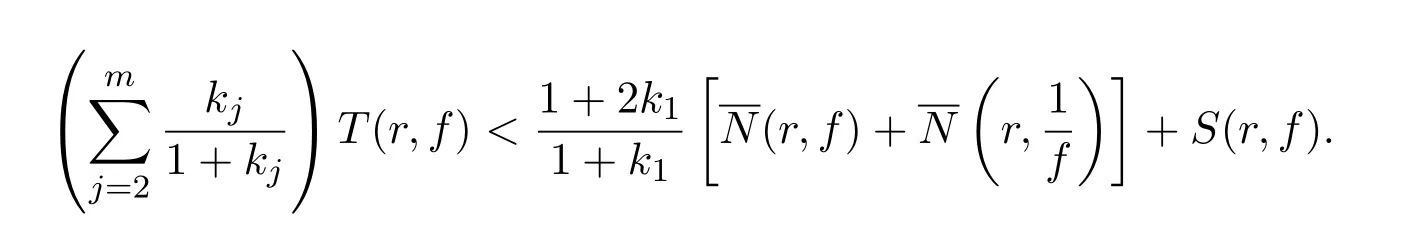
再由已知,

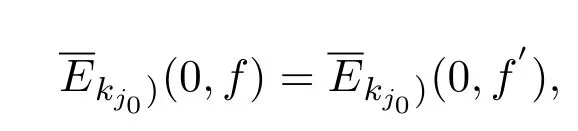
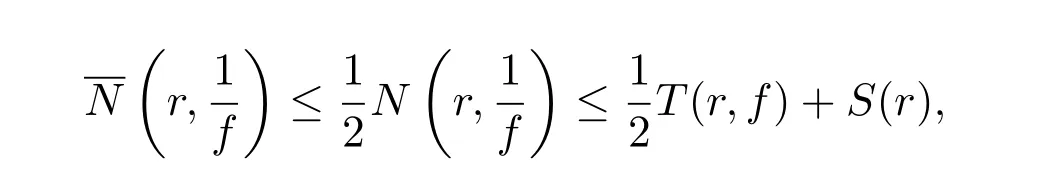
于是有

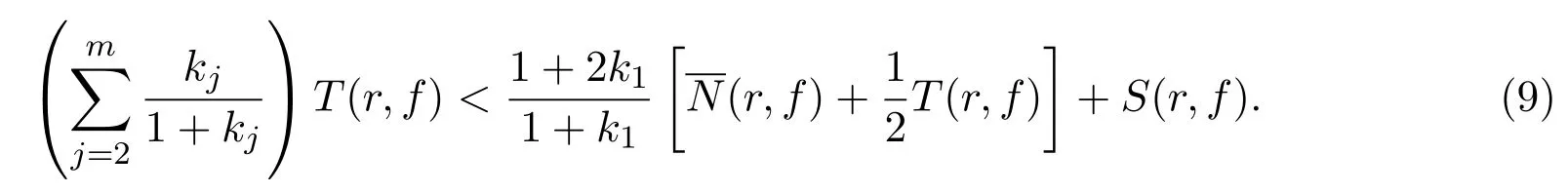
同理可得

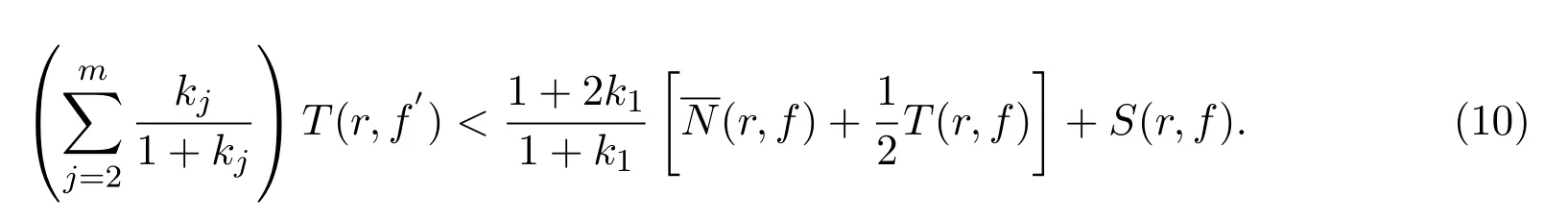
由(9)、(10)两式及已知条件,

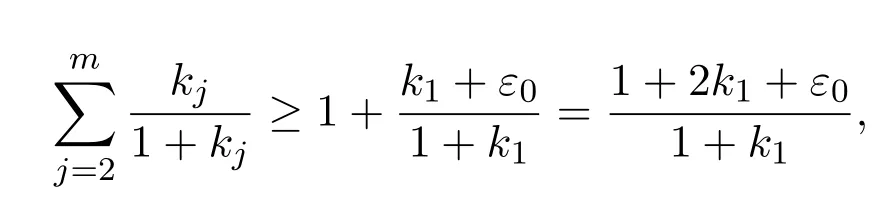
分别得

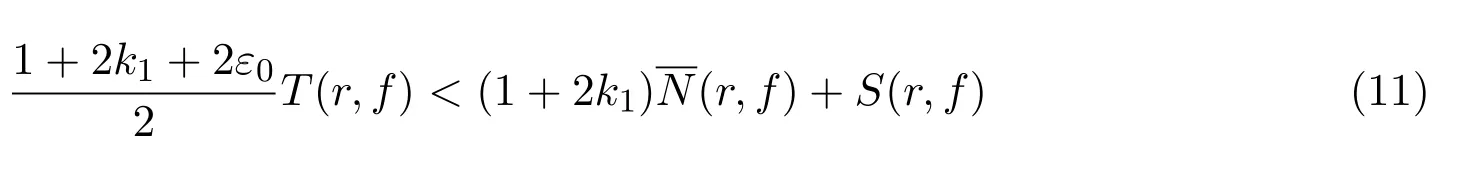
及

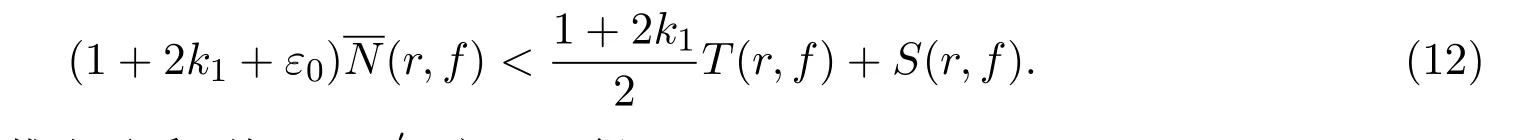
结合(11),(12)式亦推出矛盾.故f≡f′.定理1得证.

定理2的证明假设f̸≡f′.若条件(i)满足,则由引理3的(3)式知,

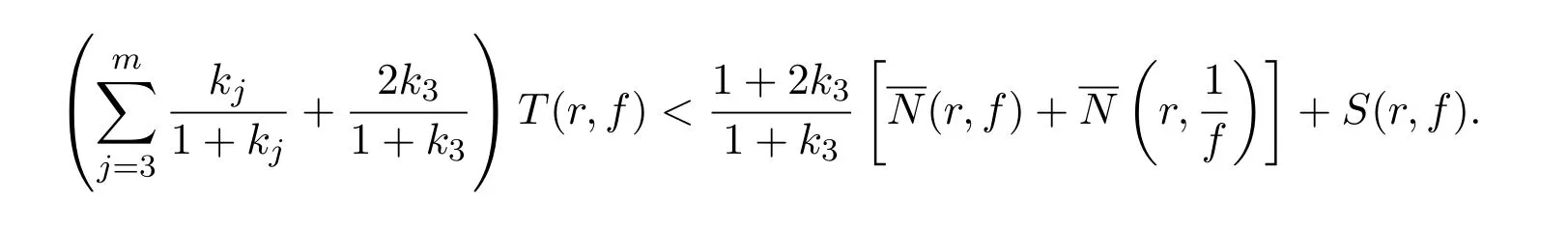
由已知条件

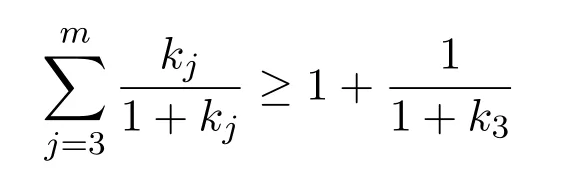
及

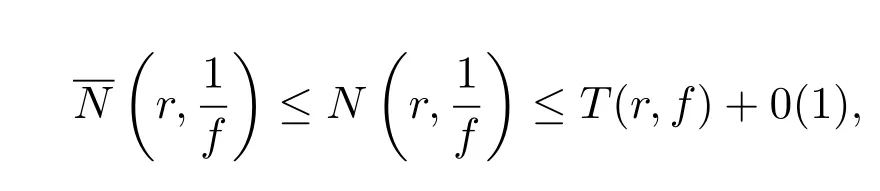
可推知

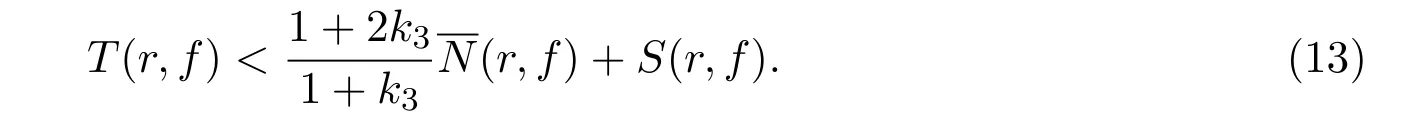
其次,类似于引理3中(i)的证明,易于推知

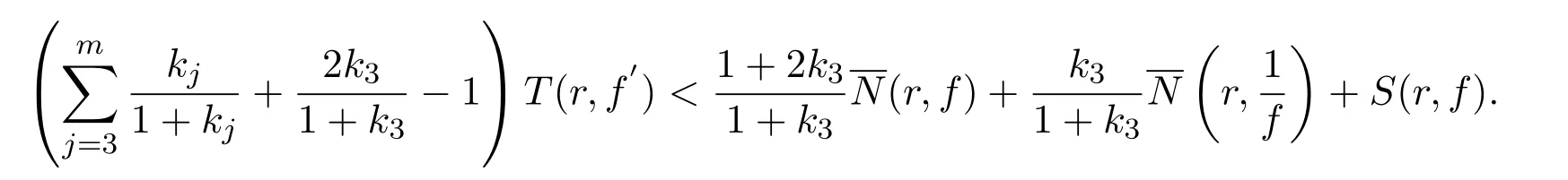
从而有

结合(13),(14)两式得

这是不可能的.若条件(ii)满足,则由引理3的(4)式,并虑及

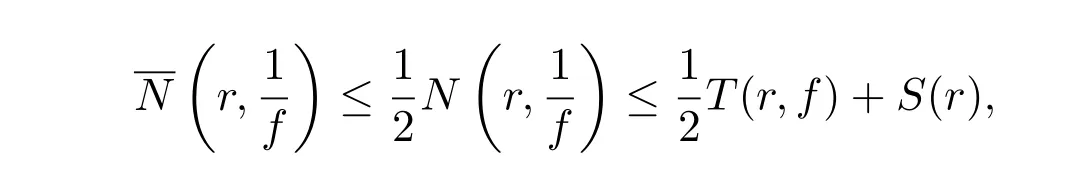
可得

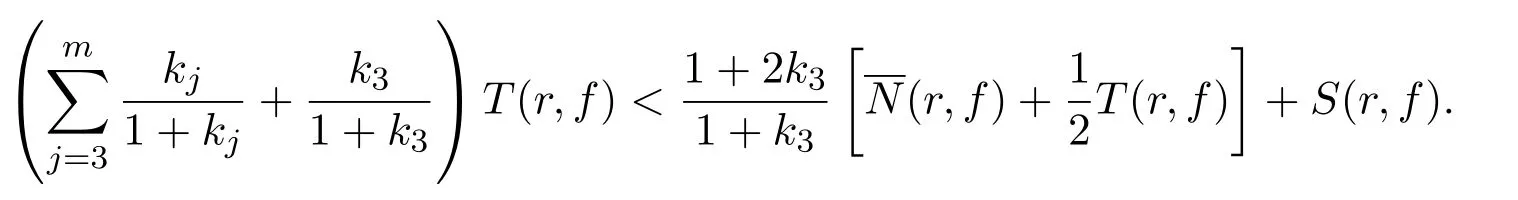
于是由已知条件

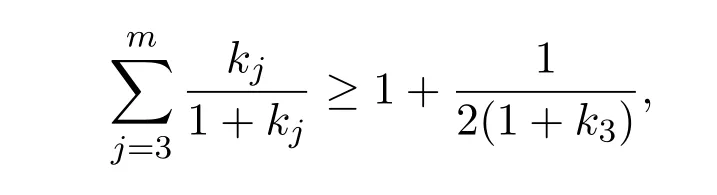
推知

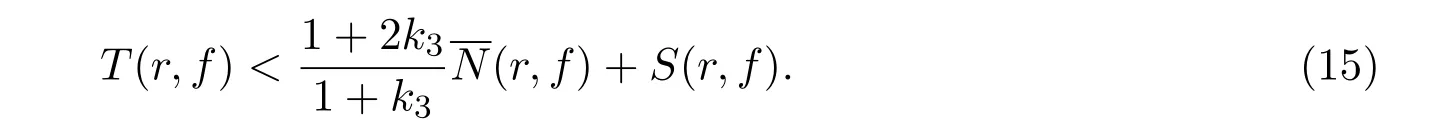
同理可得

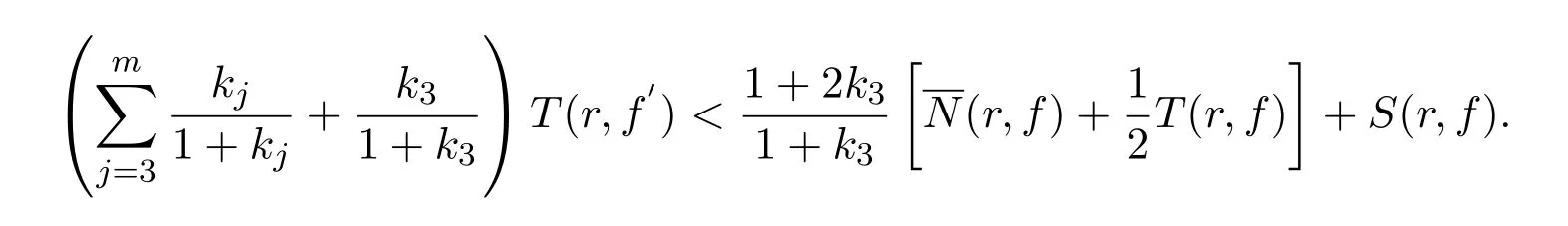
从而有

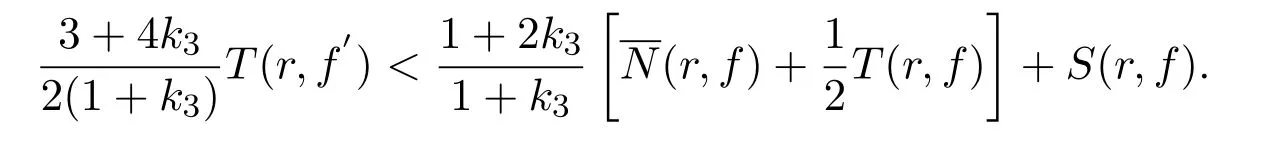
由此推出

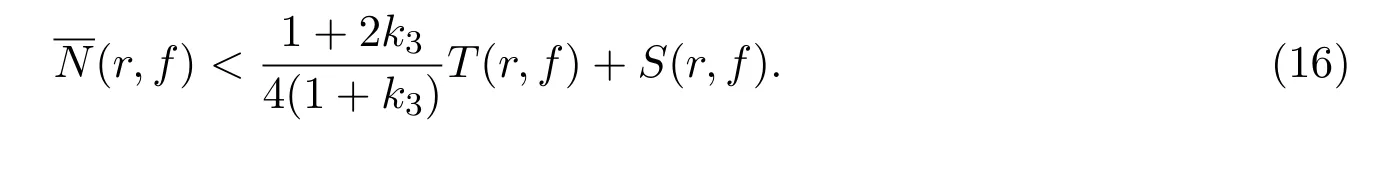
结合(15),(16)两式,得

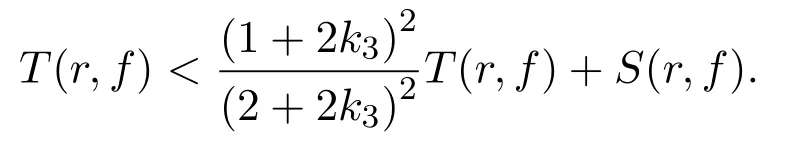
这也是不可能的.故f≡f′.

定理2得证.

[1]Hayman W K.Meromorphic Functions[M].Oxford:Clarendon Press,1964.

[2]Rubel L A,Yang C C.Values shared by an entire function and its derivatives,Complex analysis[C]//Proc. Conf.Univ.of Kentucky,Lexington Ky.,1976.Berlin:Springer,1977.

[3]Gundersen G G.Meromorphic functions that share fi nite values with their derivatives[J].J.Math.Anal. Appl.,1980,75:441-446.

[4]邱凎俤.与其导数分担三个小函数的亚纯函数[J].纯粹数学与应用数学,2004,18(20):340-343.

[5]Qiu Gandi.Meromorphic functions that share four small functions[J].Complex Analysis and Applications, 2006(1):218-224.

[6]邱凎俤.导数分担四个值的亚纯函数的唯一性[J].数学物理学报:中文版,2012,32(5):964-973.

Uniqueness of meromorphic functions that share some values with their derivatives

Tao Yixiang

(Department of Mathematics of Ningde Normal University,Ningde352100,China)

In this paper,we try to enrich the uniqueness theory of meromorphic functions and fi nd better conditions of uniqueness.Using Nevanlinna theory of meromorphic functions,we estimate more accurately the counting function of the point with n multiplicities.Then two uniqueness theorems of meromorphic functions that share some values with their derivatives are obtained,which generalize and improve some relevant results of the reference.

meromorphic function,sharing value,uniqueness

O174.52

A

1008-5513(2014)01-0084-09

10.3969/j.issn.1008-5513.2014.01.013

2013-07-15.

陶毅翔(1973-),硕士,研究方向:函数论.

2010 MSC:30D30