The wave absorption efficiency of multi-layer vertical perforated thin plates ＊

Bao-lei Geng (耿宝磊), Rong-quan Wang (王荣泉), De-zhi Ning (宁德志)

1. National Engineering Laboratory for Port Hydraulic Construction Technology, Tianjin Research Institute for Water Transportation Engineering, Tianjin 300456, China

2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024,China

Abstract: This paper analyzes the wave absorption efficiency of multi-layer perforated plates in an ideal fluid, based on the linear potential flow theory.The influence of the thickness, the porosity and the layout form of the plates on the wave absorptivity is studied on the assumption that all perforated plates are composed of the same materials and have the same thickness and porosity.The calculation results indicate that the larger the number of layers of the perforated plate set, the better the wave absorption efficiency,however, when the layer number exceeds a certain value, the efficiency of the plates is not significantly increased.For the case of porosity ε=0.2, thickness b = 0.07m and 4 layers of perforated plates with a distance l=1.0m between the layers, 90% of the energy of the wave within the incident wave period between 1.6 s and 4.4 s can be absorbed.

Key words: Wave absorptivity, multi-layer vertical plate, porous structure, analytic method

Introduction

To reduce the wave reflection and the wave force,a perforated structure is adopted in coastal engineering,this problem was studied over the past several decades by a large number of researchers by experiments,theoretical analyses and numerical simulations.

Ma[1]studied the reflection coefficient of vertical perforated breakwater structures with and without a top plate on a wave and its main influencing factors and proposed a formula for calculating the reflection coefficient and the phase difference.Koraimet al.[2]experimentally studied the hydrodynamic efficiency of a new type porous seawall by using physical models.The seawall consists of front steel screen,back solid wall and filled rock-core.Chyonet al.[3]performed experiments to investigate the interaction between wave and horizontal slotted submerged breakwater to find out the effective size and porosity of the structure for the reduction of wave height.Fang et al.[4]experimentally investigated a submerged breakwater with four-layer horizontal porous plates.In the design of the breakwater's geometrical parameters(i.e., plate submergence, porosity and width), the vertical velocity distribution of fluid particles and suggestions from previous studies were considered.The wave-dissipating characteristics, i.e., the wave reflection, transmission, energy dissipation, and vertical force coefficients, were examined in a series of experiments.The effects of layer number, breakwater width, porosity of the upper plate and incident wave height were investigated in their experimental study.

In the field of theoretical analyses, Yu and Chwang (1994) studied the water oscillation situation inside semi-circular perforated breakwaters based on the linear potential flow theory and obtained the amplitude when the perforation resistance can effectively reduce the resonance within the harbor.Subsequently, Yu (1995) calculated the diffraction action on the permeable semi-infinite breakwaters also based on the linear potential flow theory.Chwang and Chan (1998) analyzed the action between the wave and the perforated structure based on the Darcy Law and found that the perforated structure could reduce the wave generation and the resonance within the harbor.They discussed the application of this finding in engineering practice.Tenget al.[5], Liet al.[6]studied systematically the wave action using a partially porous double-wall cylinder and analyzed the influencing factors for reducing the wave surface height and the wave load.Twu and Chieu[7]developed an offshore breakwater composed of multiple layers of porous materials based on the eigenfunction expansion method.Liu and Li[8]presented an alternative analytical solution approach for water wave motion over a submerged horizontal porous plate using matched eigenfunction expansion approach.Later, Liu and Li[9]developed a new analytical solution for water wave motion through a surface-piercing porous breakwater.Karmakar and Guedes Soares[10]analyzed the multiple bottom-standing flexible porous barriers with different edge conditions to determine the performance of the wave interaction with multiple submerged barriers as breakwaters in the coastal region based on the eigenfunction expansion method.Kaligatlaet al.[11]investigated the trapping of oblique surface gravity waves by a vertical submerged flexible porous plate located near a rigid wall in water of finite as well as infinite depths by assuming that the flexible plate to be thin.Beheraet al.[12]investigated the trapping of oblique wave by porous barrier located near a rigid wall in the presence of a step type bottom bed.The physical problem is solved by using the eigenfunction expansion method and multi-mode approximation associated with modified mild-slope equation.Meng and Lu[13]studied the porous rectangular barrier on a seabed based on the linear potential flow theory and the matched eigenfunction expansion method.Manam and Sivanesan[14]studied scattering of deep water waves by a submerged or a surface piercing vertical porous barrier.Manam and Sivanesan[15]establish a new type of connection between the solutions of wave scattering problems involving vertical porous and solid barriers of same configuration.Behera and Ng[16]analyzed the performance of multiple bottom-standing flexible porous barriers in the presence of a rigid vertical wall and a step-type bottom on the basis of linearized water wave theory.Zhao et al.[17]investigated the oblique wave motion over multiple submerged porous bars in front of a vertical wall based on linear potential theory matched eigenfunction expansion method.Singla et al.[18]studied the role of partial permeable vertical barriers on the reduction of wave-induced hydroelastic response on a very large floating structure in a finite depth of water based on eigenfunction matching technique.

In the field of numerical simulations, Li and Jiang[19]studied a perforated structure in a numerical wave flume to dissipate the reflection wave with considerations of the influence of the porosity, the number of perforations, the total length of the device,and other factors on the wave dissipation efficiency.Zhanet al.[20]used the energy-dissipating property of porous media to tackle the problem of wave reflections from computational domain in the numerical wave tank.Chenet al.[21]calculated the point pressure of the wave action on the perforated plate and the reflection coefficient by utilizing a numerical wave flume based on the VOF method and thek-εturbulent model and analyzed the influencing factors for the reflection coefficient and the point pressure distribution, especially, the influence of the porosity.

Previous researches primarily focused on the correlation between the reflection coefficient, the wave force and the influencing factors under the wave action for the perforated structure, without much consideration of the influences of the porosity, the thickness and the layout form of the perforated plates on the wave absorption efficiency.The present study focuses on the influence of the porosity, the thickness and the layout form of such plates on the wave absorptivity.The proper porosity value, thickness value and layout form are proposed to improve the wave-absorbing ability of the multi-layer vertical perforated thin plates.

1.Fundamental theory and calculation method

For the wave action on a uniformly perforated plate with incident waves propagating along thex-direction at the water depthh, a plane-coordinate systemOxzis established with the originOon the static water surface and the axisOzmeasured vertically upward, as shown in Fig.1.The present study is based on the potential flow theory, and it is assumed that the perforated plates are composed of the same materials with the same thickness and porosity.In the analysis, the waveward side of the plate is set to coincide with the axisOz.

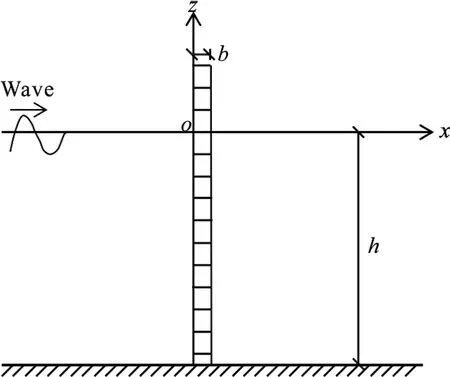
Fig.1 Schematic diagram of the action of a wave and uniformly perforated thin plates

For an ideal fluid, there is a velocity potentialφthat satisfies the Laplace equation in the whole domain.

where

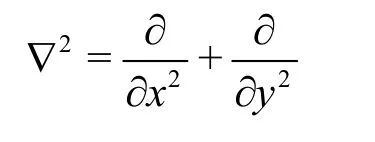
is the two-dimensional Laplacian.

The bottom of the flume satisfies the condition that the water cannot permeate the boundary of the rigid walls, that is, the normal derivative of the velocity potentialφis 0.

In the interior of uniformly perforated thin plates(i.e.,b|λ≪1, wherebis the thickness of the plate andλis the incident wave length), the fluid flow satisfies the continuity equation

and the Euler equation, with the convective term ignored

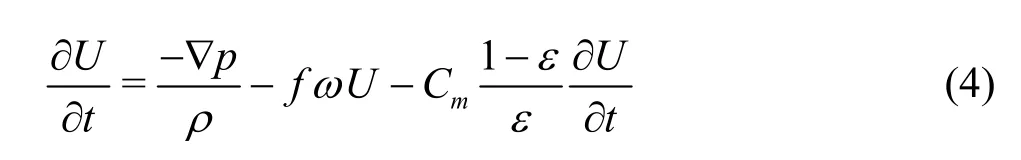
whereUis the fluid velocity,ρis the fluid density,pis the intensity of the pressure of the fluid,fis the resistance coefficient,ωis the frequency of the incident wave,Cmandεare the added mass and the porosity of the thin plate, respectively.

The time term is separated from the velocityUand the intensity of the pressurePas

The equations for the complex variableuandpare:

where

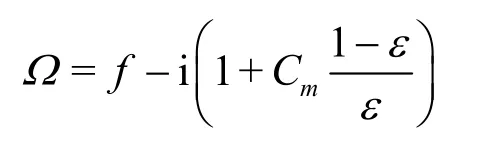
The real and imaginary parts correspond to the resistance and inertia force influences of the medium,respectively.

Provided that the water penetrates the thin plates only crosswise and the vertical component of the fluid is ignored, the relationship between the horizontal velocity and the pressure difference is as follows

where the subscripts 0 andbare the physical values in the two sides of the thin plate.

Converting the flow velocity in the perforations to the flow velocity in the whole plate, for the velocity to match with the external velocity, we have

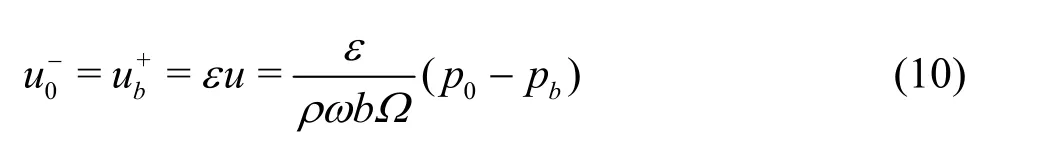
Under different circumstances, for the velocity potentials to satisfy the boundary conditions, we have the theoretical expressions of the reflection coefficient,the transmission coefficient, the energy loss coefficient and the wave absorptivity of the wave absorbing structure model of one-layer and multi-layer vertical perforated plates.Finally, comparisons, selections and optimizations are made with regard to the thickness,the porosity and the distance of the multi-layer perforated plates, based on the wave elements and other factors.

2.Modeling

2.1 Action between wave and two-layer perforated plates

Consider the two-layer perforated plates shown in Fig.2.A rectangular coordinate systemoxzis established, in which theozaxis coincides with the wave side of the first layer plate and theoxaxis is on the surface of the still water.For convenience, the computational domain is divided into 5 parts, among which1Ω,2Ωand3Ωare the external domains of the perforated plate andΩ4and5Ωare the internal domains of the 1# plate and the 2# plate, respectively.

The action between the waves and the two uniformly perforated thin plates with a thickness ofbis shownin Fig.2.The velocity potentials1φ,2φand3φwithin the areas of1Ω,2Ωand3Ωshould satisfy the following conditions:

Free water surface condition

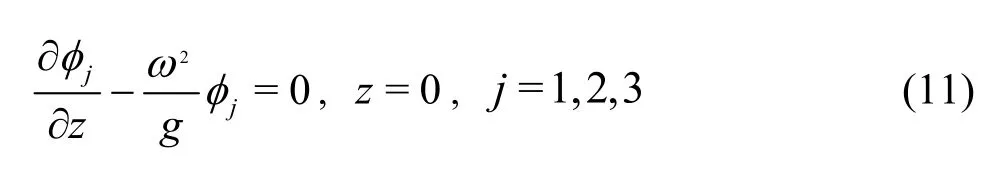
Water bottom condition

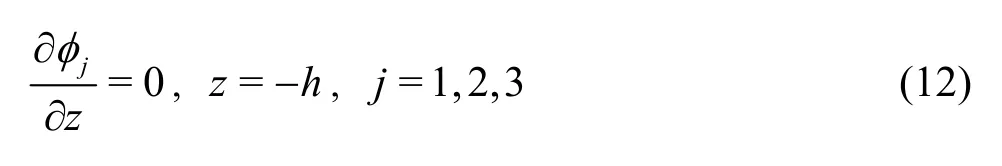
Infinity condition

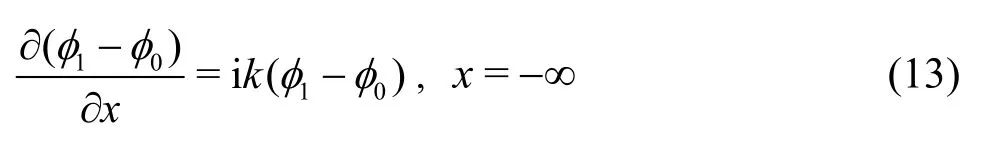
in which0φis the incident potential.

Fig.2 Schematic diagram of a wave absorbing structure with dual-layer vertical perforated plates

The object surface condition on the straight wall is

wherelmnis the distance between the No.nplate and the No.n+1 plate, the subscriptmrepresents the number of the layers of the perforated plates.

Provided that the water penetrates the thin plates only crosswise and the vertical component of the fluid is ignored, the relationship between the horizontal velocity and the pressure difference can be derived as:

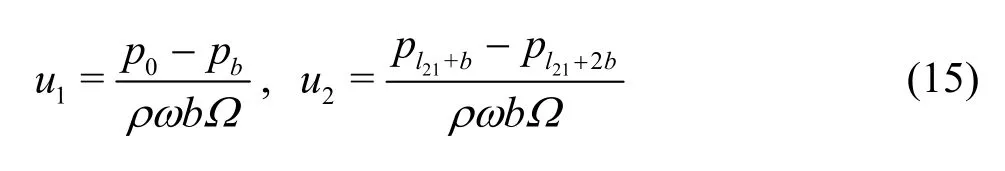
Converting the flow velocity in the perforations to the flow velocity in the whole plate, for the velocity to match with the external velocity, we have:

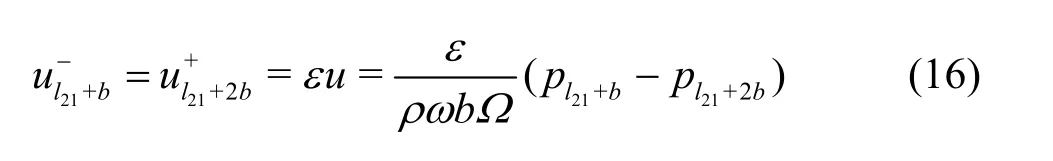
where

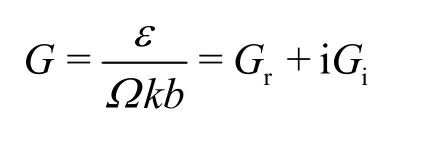
Equation (16) can be expressed as:

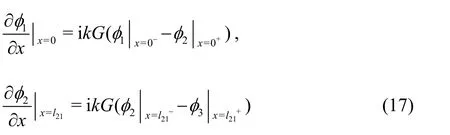
In view of the fact that the wavelength is much greater than the thickness of the perforated plates, the thickness of the thin plate is ignored, the velocity continuity condition in the thin wall can be expressed as:

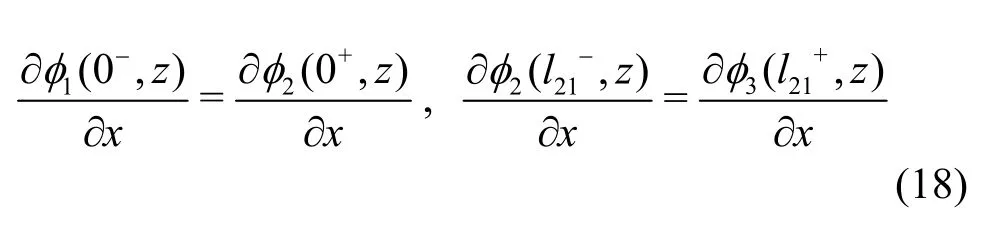
φ1,φ2,φ3exclude the evanescent-wave component,thus, they can be expressed as:

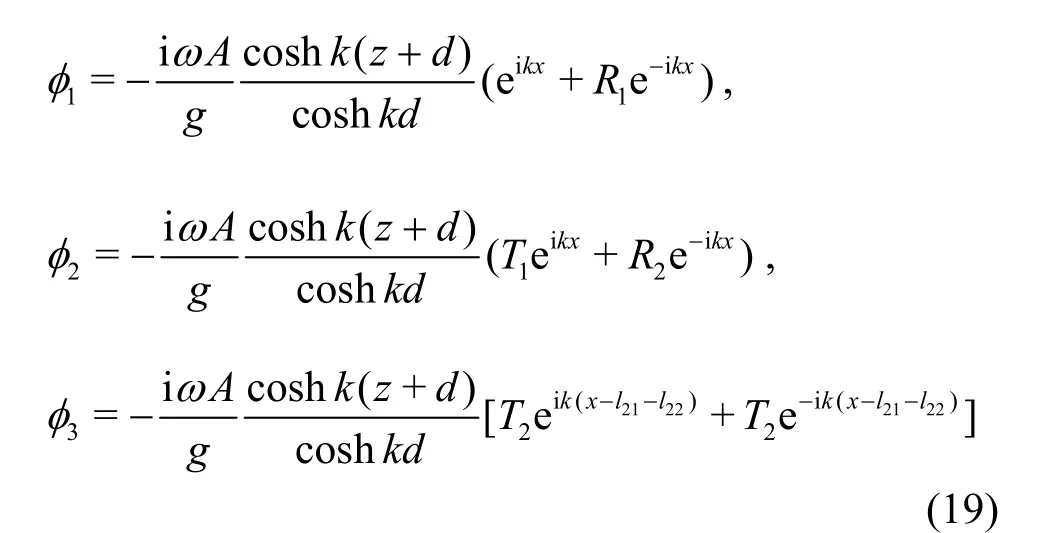
in whichR1and1Tare the reflection coefficient and the transmission coefficient of the first perforated plate, respectively,R2is the reflection coefficient of the second perforated plate, andT2is the transmission coefficient of the second perforated plate, as well as the reflection coefficient of the impermeable straight wall under the total reflection condition.

Substituting the velocity potentials1φ,2φ,3φinto Formula (17) and Formula (18), we have:

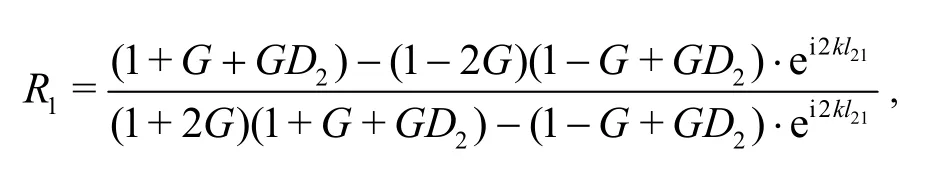
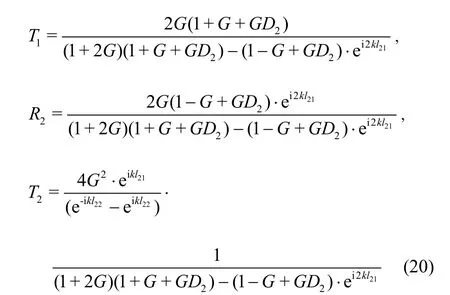
where

Regarding all perforated plates as an entire wave absorbing structure.the reflection coefficientKrand the transmission coefficientKtof the structure can be written as:

The energy loss coefficient is

The wave energy absorbed by the wave absorbing structure is defined as the sum of the loss and transmission energies, and the absorptivity is

2.2 Action between the wave and different perforated plates

The reflection coefficient and the transmission coefficient of the incident wave when one layer, three layers and four layers of perforated plates are used can be obtained by using the same method.Figure 3 shows the schematic diagrams of the action between the wave and different-layer perforated plates, and the relevant formulas for describing the coefficients are as follows:

(1) When we have one layer of perforated plate

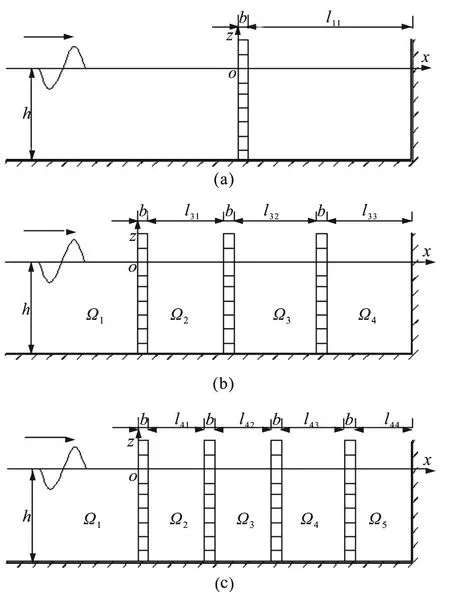
Fig.3 Schematic diagrams of different-layer perforated plate layouts

The reflection coefficientKrand the transmission coefficientKtare:

(2) When we have three layers of perforated plates

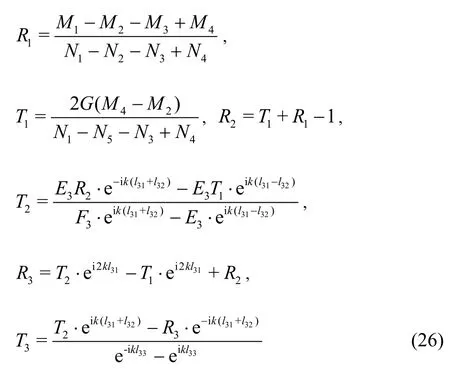
where

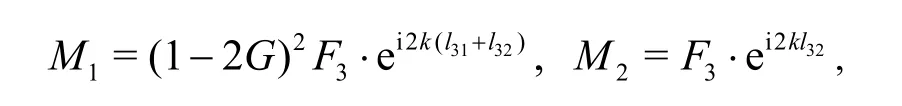
The reflection coefficientKrand the transmission coefficientKtof the wave absorbing structure are:

(3) When we have four layers of perforated plates

in which

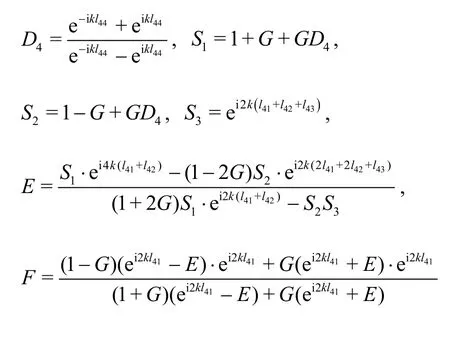
The reflection coefficientKrand the transmission coefficientKtof the absorbing structure to the

wave are:

For the action between the wave and differentlayer perforated plates, the expressions of the system energy loss coefficient and the absorptivity are the same as shown in Formulas (22), (23).

3.Examples

3.1 Influences of the number of layers of the perforated plates on the wave dissipation efficiency

Consider multilayer plates, with each plate of the same characteristics, i.e., of the same material, thickness and porosity.The depth of the water is 2.5 m and the maximum width (i.e., the total width of the wave absorbing structure) for setting the perforated plate is 12 m.

To study the influences of the number of layers of the perforated plates on the wave dissipation efficiency, calculations are performed to determine the wave dissipation efficiency when different layers of the perforated plates have different values of porosityεand thicknessb.According to Yu (1995), the resistance coefficient and the added mass aref=2.0 andCm=0, respectively.For the optimal positions of the perforated plates with an equal distance in the 12 m wave dissipation area when the incident period is 3.5 s,Fig.4 shows the reflection coefficientKrand the absorptivityKaagainst the porosityεand the thicknessbof the perforated plates.

From Figs.3(a), 3(c), we can see that when the incident wave period is 3.5 s, the reflection coefficientKrdecreases and then increases with the increase of the porosityε.Such behavior is due to the fact that when the porosity of the perforated plate is small,much of the wave is reflected, whereas when the porosity of the perforated plate is large enough, the perforated plate is equivalent to a permeable structure and all waves are reflected by the vertical wall behind the perforated plate.The variation of the absorptivityKais opposite to that of the reflection coefficientKr, i.e., the absorptivityKaincreases and then decreases with the increase of the porosityε.The reflection of the structure will decrease with the increase of the number of perforated plates; however,the absorptivity will increase, indicating that multilayer perforated plates have a better wave dissipation efficiency.The wave absorption efficiency is best when the number of plates is four and the porosity is approximately 0.2, as shown in Figs.3(a), 3(c).

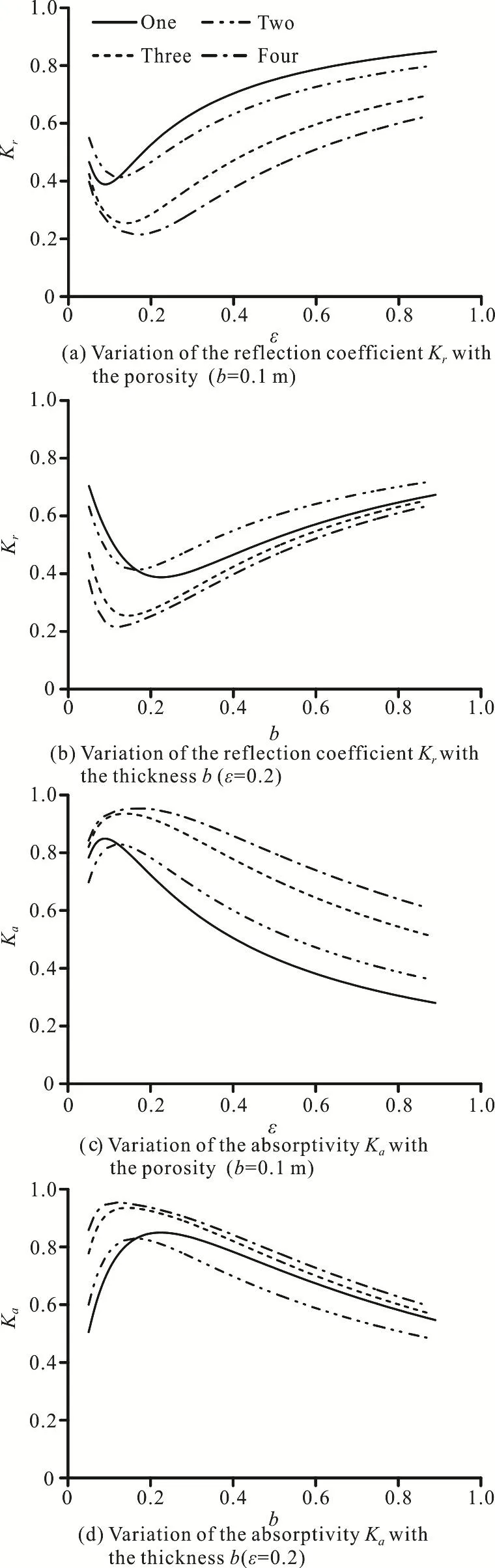
Fig.4 Effects of the porosity and thickness of the plate on the absorptivity efficiency of the plates

The reflection coefficientKrdecreases and then increases with the increase of the thickness of the perforated plates, whereas the variation of the absorptivityKais opposite to that of the reflection coefficientKr, i.e., the absorptivityKaincreases and then decreases.Overall, when the thicknessbremains unchanged, the reflection coefficient will decrease and the absorptivity will increase with the increase of the number of layers of the perforated plates, indicating that multilayer perforated plates have a better wave dissipation efficiency.A slight reduction of the reflection coefficient of the multilayer perforated plates of four layers is observed compared with that of three layers, indicating that more layers of plates have a very small influence on the reduction of the reflection coefficient when the number of layers reaches three.

3.2 Influence of the thickness of the perforated plates on the wave absorptivity

We now consider the influence of the perforated plates with different parameters (thickness, porosity and spacing) on the wave absorption efficiency with an incident period between 0.5 s and 5.0 s when four layers of perforated plates are considered.The resistance coefficient and the added mass are stillf=2.0 andCm=0, respectively (Yu (1995)).

Fig.5 Influence of the thickness of the perforated plates on the wave absorptivity

Assume that the four layers of perforated plates are with an equal spacing,l=1.0m, and the porosity of the perforated plates isε=0.2.The influence of the thickness of the perforated plates on the wave absorptivity with the incident periods from 0.5-5.0 s is shown in Fig.5.The wave absorptivity decreases with the increase of the thickness in the short wave region,whereas in the long wave region the trend is opposite.It is found that when the thickness is 0.07 m (i.e.,b= 0.07m), the perforated plate structure has a good wave absorption efficiency in a relative long wave period region; in addition, the absorptivity of the wave with an incident period between 1.6 s and 4.4 s will reach and exceed 90%, among which the highest absorptivity is over 95%.

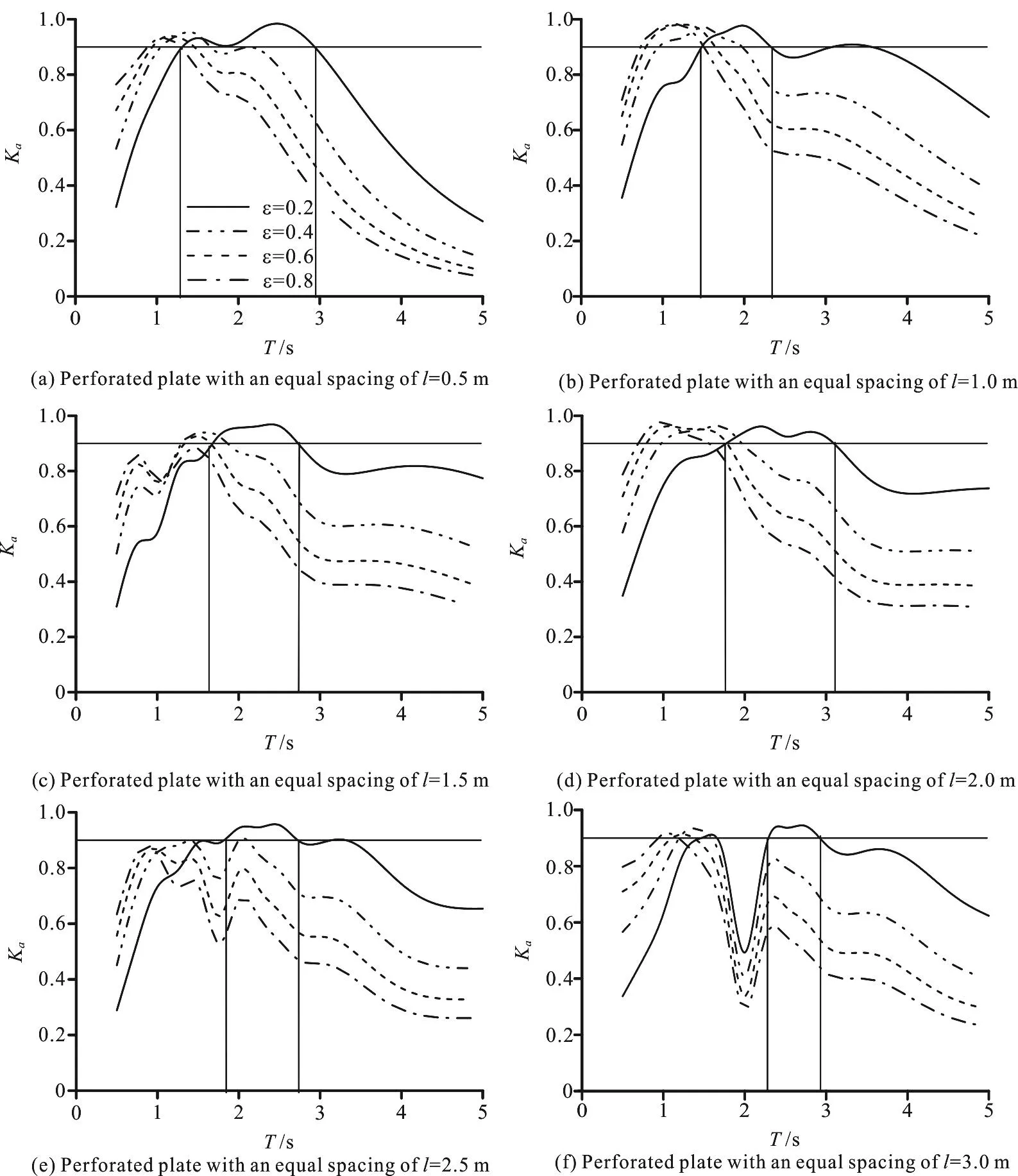
Fig.6 Influence of porosity and plate spacing on wave absorptivity (b=0.05m)

3.3 Influence of porosity and plate spacing on wave absorptivity

The influence of the porosity and the plate spacing on the wave absorptivity is considered in this subsection for perforated plates of four layers.Figures 6, 7 show the variations of the absorptivity versus the incident wave period at a plate thickness of 0.05 m and 0.07 m (b= 0.05m ,b=0.07m) for different values of the porosity and the plate spacing.

We can see that the relation curves see a left-ward shift overally with the increase of the porosity.For the short period waves, the larger the porosity, the better the wave absorption efficiency, in contrast, for the long period waves, the absorptivity decreases with the increase of the porosity.The wave absorption efficiency of the structure is best when the porosity is 0.2, i.e.,ε=0.2, for which the period of an incident wave with an absorptivity over 90%reaches the maximum.

Among plates with different spacings, the wave absorption efficiency of the structure is the best when the plate spacing is 1.0 m (i.e.,l=1.0m), in other words, the period range of an incident wave with an absorptivity over 90% reaches the maximum.The period range of an incident wave with an absorptivity over 90% will decrease when the plate spacing increases or decreases.

Moreover, from Figs.6, 7, we can see that the structure will satisfy the design requirements better and reach a larger period range of the effective incident wave as indicated by the wave absorption requirements when the plate spacing is 1.0 m and the thickness is 0.07 m (i.e.,l=1.0m,b= 0.07m).Whenb=0.05m ,T∈ ( 1.4s,2.4s), whenb=0.07m,T∈ ( 1.6s,4.4s).

Fig.7 Influence of porosity and plate spacing on wave absorptivity (b=0.07m)

4.Conclusions

Based on the analytical studies, it is found that the absorptivityKaincreases with the increase of the number of layers of perforated plates.However, the increase of the wave absorption efficiency is not significant when the number of layers of plates increases from 3-4.Thus, we consider 4 layers of perforated plates.

For incident waves with a short period, the absorptivityKais found to decrease with the incincrease of the plate thicknessb,and increase with the increase of the porosityε.For incident waves with a long period, the absorptivityKais found to increase with the increase of the plate thicknessb,but decrease with the increase of the porosityε.It is shown that when the porosity is 0.2, the plate thickness is 0.07 m, and the adjacent spacing between the four layers of the perforated plates is 1.0 (i.e.,the wave absorption efficiency for a wave with an incident period of (1.6 s, 4.4 s) will reach 90% (even exceeding 95% for some incident wave periods).

Acknowledgement

This work was supported by the Central Commonwealth Research Institute Basic R&D Special Foundation of TIWTE (Grant No.TKS160107).