Pdn（n=1～9）团簇的结构及磁性的第一性原理计算

温俊青，姚 攀，李东明，王小青

（1.西安石油大学理学院，西安710065；

2.西北大学化学与材料科学学院，西安710069）

1 引 言

金属钯作为一种4d 过渡金属，是许多有机催化剂的活性组成部分，同时钯还是制造电子工业产品中一种重要的稀有金属，多年以来一直受到化学和材料科学工作者的广泛关注［1-6］.Garcia-Rodeja等人［7］运用EAM 势研究了Pdn（n=2～23）团簇的结构、结合能和熔化特征；Irena等人［8］对Pdn（n=2～13）团簇的电子结构和能量进行了研究；Karabacak 等人［9］利用原子嵌埋法研究了Pdn（n=2～20）团簇的稳定结构和能量性质；郭向云等人［10］利用蒙特卡罗方法以及LJ+AT 势研究了处于气相中的钯团簇的结构演化和生长规律；José等人［11］利用遗传算法研究了纯Pdn（n=2～13）小团簇的结构随团簇尺寸增大的演变规律；Efremenko［12］等人运用EH 方法研究了小Pdn团簇的结构和稳定性.钯作为与铁磁性元素镍同族的元素对其磁性的研究的报道也很多［13-16］.Reddy等人首次从理论上发现4d 非磁性元素Pd，Rh，Ru 团簇均具有较大的磁矩［13］，Douglass等人利用Stern-Gerlach实验精确测量了非磁性元素Al，Cr，Pd，V 团簇的磁矩大小，结果显示Al，Cr，Pd，V 团簇都具有一定大小的固有磁矩［14］.最近，Shinohara等人［16］报道Pd团簇具有大的磁矩，与Reddy等人的研究相一致，但与实验结果不符.

课题组已经研究了镍及掺杂的镍团簇的结构、磁性等性质［17，18］.进一步研究钯团簇，可以清楚地理解这一簇团簇的生长规律及性质变化.本文采用基于第一性原理的密度泛函理论（DFT）中的广义梯度近似（GGA）泛函中的BPW91泛函及三参数杂化泛函B3LYP，及Hay和Wadt提出的适合重元素的计算的相对论有效核势基组LANLZD［19］对Pdn（n=1～9）团簇的结构进行了全面优化，并对两种泛函得到的结果进行了比较.

2 计算方法

为了确定所选方法的可靠性，分别选用不同交换关联泛函，基组是LANL2DZ，计算了Pd2团簇的键长和结合能，并与实验结果进行了比较（表1）.对Pd2团簇实验得到基态为三重态，键长为2.48Å［20］，对结合能，Lin等人［21］报告为0.366 eV／atom，而Ho 等 人 的 报 告 为0.515eV／atom［22］.从 表1 可 以 看 到 局 域 密 度 近 似 泛 函SVWN 方法得到的键长与实验值接近，但结合能与实验值相差较远.杂化密度泛函和广义梯度近似交换关联泛函得到的键长与实验值相差基本相同，但杂化密度泛函得到的结合能在实验值0.366 eV／atom 和0.515eV／atom 之间，而广义梯度近似交换关联泛函得到的结果与实验值0.515eV／atom 更接近，所以我们选用GGA 中的BPW91泛函和杂化密度泛函B3LYP对Pdn团簇的结构进行优化.

表1 不同交换相关泛函下优化的Pd2团簇的键长R（Å），结合能Eb／（eV／atom）的理论值和实验值Table 1 The calculated values with different exchangecorrelation functional and experimental data of bond length R（Å），binding energy Eb（eV／atom）for Pd2cluster

3 计算结果与分析

在本节中我们运用密度泛函理论方法，在BPW91／LANL2DZ和B3LYP／LANL2DZ水平下对Pdn（n=1～9）小团簇的结构进行了全面优化，得到了Pdn（n=1～9）小团簇的一系列稳定结构，见图1.并分析了Pdn（n=1～9）小团簇的结构、稳定性和磁性等随团簇尺寸的变化规律.Pdn（n=1～9）小团簇的最低能量结构和亚稳态结构的结构参数见表2、表3.

3.1 几何结构

Pd3：对Pd3团簇，BPW91方法优化得到Pd3团簇的最低能量结构为具有C2v对称性的一个开环结 构（3a），腰 长 为2.519 Å，顶 角 达 到 了179.95°，构型与直线性相似.具有Cs对称性的三角形（3b），平均键长为2.643 Å，三个角依次为69.29°，57.07°和53.63°，能量比开环结构（3a）高0.272eV.上述结构都为自旋五重态.

B3LYP方法得到Pd3团簇的最稳定结构与BPW91方法不同，最稳定结构为具有Cs对称性的三角构型（3b），平均键长为2.620Å，三个角中最大一个角为65.42°，结合能为0.852eV／atom.两种方法得到Pd3团簇的基态结构不同，与我们所选用方法有关.文献［8，9，23］得到Pd3团簇的基态结构也都为三角构型，说明运用B3LYP 泛函计算Pd3团簇结构精确.

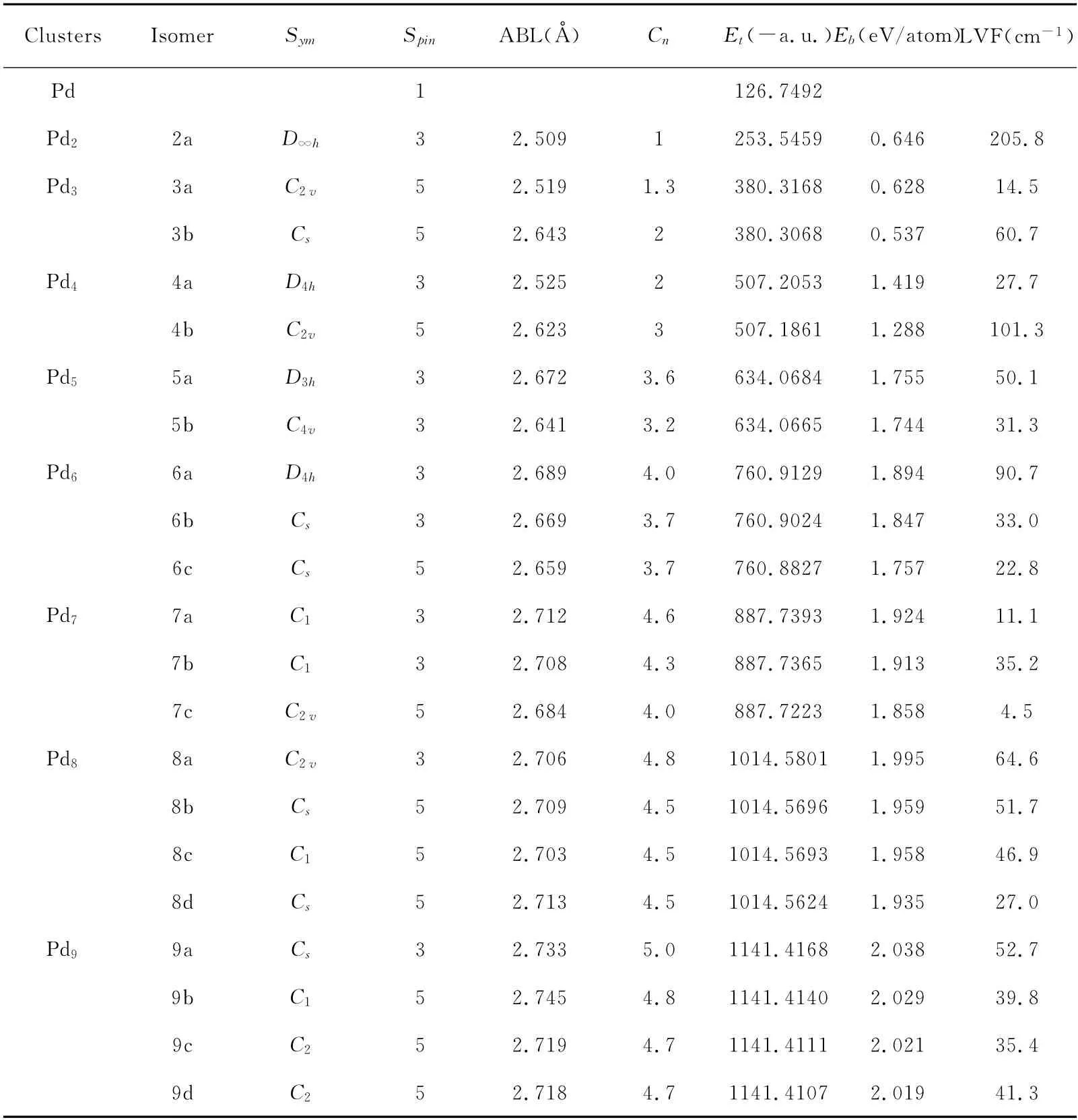
表2 BPW91／LANL2DZ水平下优化的Pdn（n=1～9）团簇的对称性（Sym），自旋多重度（Spin），平均键长（ABL／Å），平均配位数（Cn），总能（Et／（-a.u.）），结合能（Eb／（eV／atom）），频率（LVF／cm-1）Table 2 Symmetry（Sym），spin multiplicity（Spin），average bond length（ABL／Å），average coordination number（Cn），total energy（Et／（-a.u.）），bingding energy（Eb／（eV／atom）），vibrational frequency（LVF／cm-1）of Nin（n=1～9）clusters at BPW91／LANL2DZ level

表3 B3LYP／LANL2DZ水平下优化的Pdn（n=1～9）团簇的对称性（Sym），自旋多重度（Spin），平均键长（ABL／Å），平均配位数（Cn），总能（Et／（-a.u.）），结合能（Eb／（eV／atom）），频率（LVF／cm-1）Table 3 Symmetry（Sym），spin multiplicity（Spin），average bond length（ABL／Å），average coordination number（Cn），total energy（Et／（-a.u.）），bingding energy（Eb／（eV／atom）），vibrational frequency（LVF／cm-1）of Pdn（n=1～9）clusters at B3LYP／LANL2DZ level

Pd4：对Pd4团簇，BPW91方法优化得到Pd4团簇的最稳定结构为具有D4h对称性的正方形结构（4a），平均键长为2.525 Å，结合能为1.419 eV／atom，是一个自旋三重态.由于Jalln-Teller效应使团簇对称性降低，具有C2v对称性的四面体结构较稳定（4b），平均键长值也仅相差0.001Å，且两者都为五重态，（4b）结构的能量比（4a）高0.522eV.

B3LYP方法得到Pd4团簇的最稳定结构也与BPW91方法不同，由于Jalln-Teller效应使最稳定结构畸变为具有Cs对称性的四面体结构（4b），是一个自旋三重态，平均键长为2.660Å，结合能为1.248eV／atm.第二低能构型为具有D4h对称性的正方形结构（4a），平均键长为2.534Å，结合能为0.984eV／atom，能量比（4a）高1.054eV.Irena等人［8］运用量子化学的方法也得到Pd4团簇的基态结构为具有C3v对称性的四面体，次稳定结构为具有D4h对称性的正方形结构.文献［9，23］也发现Pd4团簇的最稳定结构为四面体结构，与B3LYP方法所得基态结构相同.

Pd5：对Pd5团簇，BPW91方法得到Pd5团簇的最稳定结构为具有D3h对称性的三角双锥结构（5a），是一个自旋三重态，平均键长为2.672Å，结合能为1.755eV／atom.具有C4v对称性的四方锥结构是一个亚稳态结构（5b），自旋多重度也为3，能量比（5a）仅高0.052eV.

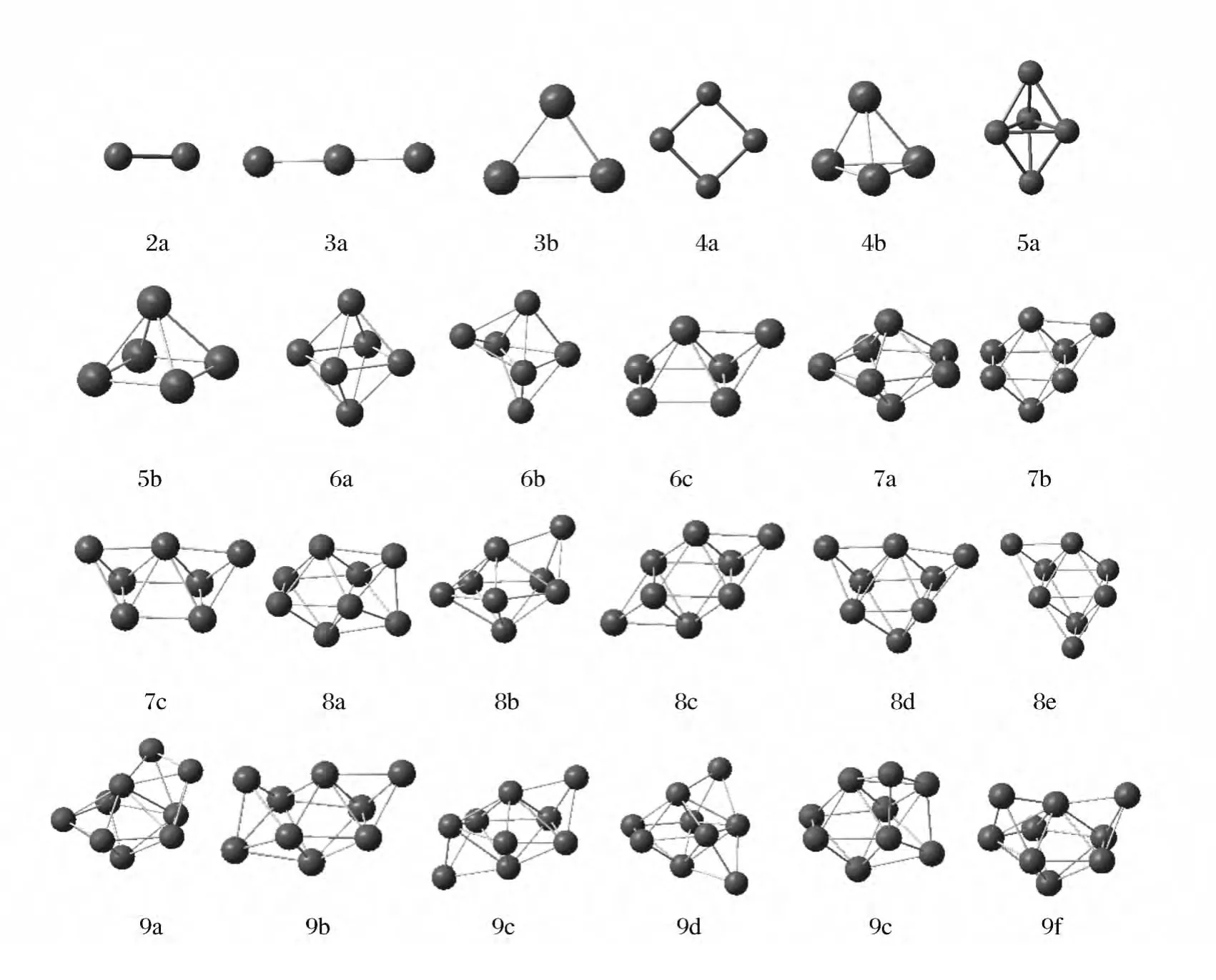
图1 优化得到的Pdn（n=1～9）团簇的稳定构型Fig.1 Stable structures of Pdn（n=1～9）clusters

B3LYP方法得到Pd5团簇的最稳定结构也为自旋三重态的三角双锥结构（5a），由于Jalln-Teller效应使对称性降为Cs，平均键长为2.755 Å，结合能为1.322eV／atom.具有C4v对称性的四方锥结构是第二低能结构（5b），是一个自旋三重态，能量比（5a）结构高0.111eV.Futschek等人［23］和Irena等人［8］发现Pd5团簇的两个几乎简并的基态结构为三角双锥结构和四方锥结构.文献［9］报道仅发现Pd5团簇的一个稳定结构为三角双锥结构，结合能为1.46eV／atom.

Pd6：BPW91方法得到Pd6团簇的最稳定结构为结合能为1.894eV／atom，平均键长为2.689 Å，具有D4h对称性的八面体结构（6a），是一个自旋三重态.具有Cs对称性的戴帽三角双锥结构（6b）是第二低能结构，能量比（6a）高0.286eV，戴帽四方锥结构（6c）能量比（6a）高0.822eV，是第三低能结构.

B3LYP方法得到Pd6团簇的基态结构也是具有D4h对称性的八面体结构（6a），并且也是一个三重态，平均键长为2.717Å，比BPW91方法的长0.028Å，结合能为1.409eV／atom.第二低能结构为戴帽四方锥结构（6c），能量比（6a）高0.827 eV.Karabacak等人［9］运用MD 方法得到Pd6团簇的基态结构为八面体结构，结合能为1.17eV／atom.文献［8］得到Pd6团簇的基态结构为八面体结构，平均键长为2.59Å，结合能为1.82eV／atom.文献［9，23］得到Pd6团簇的基态结构也为八面体结构.

Pd7：BPW91方法得到Pd7团簇的前三个稳定结构的顺序依次为五角双锥结构（7a），面心戴帽八面体结构（7b），面心两戴帽四方锥结构（7c），平均键长分别为2.712Å，2.708Å 和2.684Å，结 合 能 为1.924eV／atom，1.913eV／atom 和1.858eV／atom.结构（7a）的能量分别比（7b）和（7c）低0.076eV 和0.463eV.

由表3可知，四个维度之间均呈现中度正相关，除了对学习效果满意度维度外，其他3个维度均存在非常显著意义(P<0.01).说明本量表各维度间所测量的心理特质相对独立，也说明本量表具有良好的结构信度.

B3LYP方法所得结构与BPW91方法完全相同，最稳定结构为五角双锥结构（7a），平均键长为2.749Å，结合能为1.438eV／atom.（7a）结构的能量分别比另两个亚稳态结构面心戴帽八面体结构（7b）和面心两戴帽四方锥结构（7c）低0.099 eV 和0.909eV.Karabacak等人［9］运用MD 方法得到Pd7团簇的基态结构为五角双锥结构，结合能为1.86eV／atom.Irena等人［8］运用量子化学的方法得到Pd7团簇的前两个稳定结构为五角双锥结构和两戴帽四方锥结构，结合能分别为1.95eV和1.81eV.文献［23］得到Pd7团簇的基态结构也为五角双锥结构.

Pd8：对Pd8团簇，BPW91方法得到Pd8团簇的最稳定结构为上下相邻两个面心戴帽的双戴帽八面体结构（8a），它的自旋三重态是基态结构，相应平均键长为2.706Å，结合能为1.995eV／atom.与文献［9］得到Pd8团簇的双戴帽八面体结构相同.第二低能异构体为戴帽五角双锥结构（8b），能量比基态结构高0.285eV.Pd8团簇的第三，四低能结构也都为两戴帽八面体结构（8c，8d），两个帽戴在八面体的位置不同，使能量略有差别，能量分别比（8a）高0.293eV 和0.482eV.

B3LYP 方法得到Pd8团簇的基态结构与BPW91方法相同，也为上下相邻两个面心戴帽的双戴帽八面体结构（8a），平均键长为2.737Å，结合能为1.459eV／atom，比BPW91 方法得到的（8a）结构的平均键长大.第二稳定结构为上下相对的两个面心戴帽八面体结构（8c），能量比（8a）高0.032eV／atom.第三稳定结构为戴帽五角双锥结构（8b），能量比（8a）高0.070eV／atom.（8d）为第四稳定结构，能量比（8a）高0.194eV／atom.文献［23］得到Pd8团簇的基态结构为两戴帽八面体结构（与8a相同）.

Pd9：Pd9团簇的稳定结构保持了Pd8的基本框架，都是在Pd8团簇的稳定结构的基础上添加原子形成的.BPW91方法得到Pd9团簇的最稳定结构为具有Cs对称性的两戴帽五角双锥结构（9a），两个帽戴在五角形面的同一侧的相邻的两个面心上，平均键长为2.733Å，结合能为2.038eV／atom，此结构可看作是在（8b）结构的基础上增加一个原子得到.第二低能结构为三戴帽的八面体结构（9b），此结构可看作是在（8a）结构的基础上增加一个原子得到，结合能为2.029eV／atom，能量比（9a）仅高0.076eV，能量几乎是简并的.第三，四低能结构也都为两戴帽五角双锥结构（9c，9d），说明戴帽的位置不同，使能量略有差异，结构（9c）和（9d）能量分别比（9a）高0.155eV 和0.166eV.

B3LYP方法也得到了和BPW91方法相同的四个稳定结构，最稳定结构为三戴帽八面体结构（9b），平均键长为2.757Å，结合能为1.504eV／atom，能量分别比另三个次稳定结构（9a，9c，9d）高0.004eV，0.051eV 和0.254eV，（9b）与（9a）结构能量仅差0.004eV，几乎是简并的，所以在实验上这两种结构是并存的.文献［8］得到Pd9团簇的稳定结构为两戴帽五角双锥结构，结合能为2.08eV／atom.文献［23］得到Pd9团簇的两个稳定结构为两戴帽五角双锥结构和双三角反棱柱结构（同结构9b）.文献［9］得到Pd9团簇的基态结构为在八面体结构的基础上生成.

采用广义梯度近似（GGA）泛函中的BPW91泛函和三参数杂化密度泛函B3LYP优化了Pdn（n=1～9）团簇的结构，两种方法得到了完全相同的稳定结构，除n=3、4外，两种方法得到的基态结构是完全一致的.但在n=3、4时用三参数杂化密度泛函B3LYP 得到的基态结构与文献［8，9，23］的相同，说明两种泛函都可以描述小的Pdn（n=1～9）团簇的结构演化规律，但三参数杂化密度泛函B3LYP对小的Pdn团簇的结构描述更精确.

3.2 结构演化分析

团簇的性质和团簇的基态结构及能量是密切相关的，为了研究团簇结构的演化规律，我们计算了Pdn团簇的平均键长ABL／Å，平均配位数CN，并绘在图2和图3中.可以看到B3LYP方法得到的平均键长比BPW91方法要长，且团簇的平均键长都随团簇尺寸增加而增加，在n=2～5，两种方法得到的平均键长都发生了明显的增加，n=5～9，平均键长随团簇尺寸有一定振荡.在n=7，9时两条曲线都为峰值，n=6，8时为谷底，这也可以从结构演化中得到解释.n=7，9时两种方法得到的结构都为五角双锥和两戴帽五角双锥结构，n=6，8时为八面体和两戴帽八面体结构，n=7，9时的峰值说明了团簇基态结构生成的一种模式-在十面体的基础上生成，n=6，8时为在八面体的基础上生成.从图中也可以看到两种方法得到的平均配位数也随尺寸的增大而增大，Pd9的平均配位数达到了5.0，但比Pd块体的配位数12小许多.在n=2，5，6，7，8时两种方法得到的配位数相同，说明在此尺寸时团簇具有相同的基态结构，n=3，4 时平均配位数不同，因为在n=3 时，BPW91方法得到团簇的基态结构为一个近似直线性的开环结构，而B3LYP方法为锐角三角形，在n=4时，BPW91方法得到团簇的基态结构为正方形，而B3LYP方法为四面体结构，平均配位数不同也可以说明团簇结构的不同.B3LYP方法得到Pd9团簇两个能量几乎简并的基态结构为三戴帽八面体结构和两戴帽五角双锥结构，在计算配位数时我们是按三戴帽八面体结构计算的，所以导致两种方法得到的配位数不同.平均键长和平均配位数都随团簇尺寸增大说明团簇通过增加原子而使其尺寸增大，键长增大会降低团簇的束缚能，为了使团簇的束缚能增加可以通过增加团簇的成键数达到，即使配位数随团簇尺寸而增加.

图2 平均键长随团簇尺寸的变化Fig.2 Average bond length changes with the size of clusters

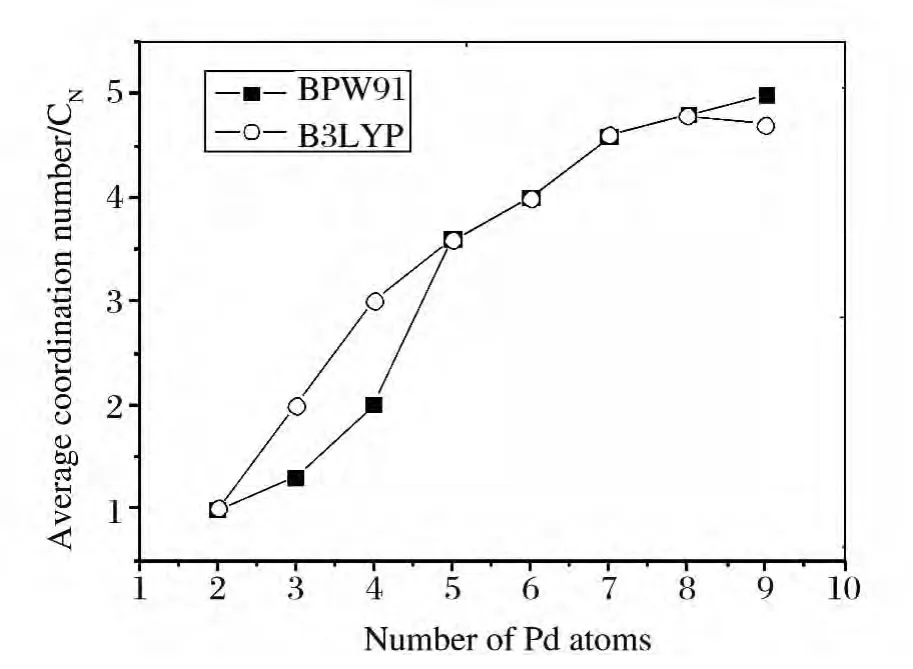
图3 平均配位随团簇尺寸的变化Fig.3 Average coordination number changes with the size of clusters

3.3 相对稳定性分析

从图中可以看到，除n=3外，两种方法得到的平均结合能随团簇尺寸的变化规律是相似的，即都随团簇尺寸的增大而增大，说明团簇的稳定性也随尺寸的增大而增强.除n=3外，B3LYP方法得到Pdn团簇的平均结合能（Eb）都低于BPW91方法的结果.在n=2～5，两种方法得到的结合能均有明显的增大，从n=5开始增幅随尺寸的增加在减小，且曲线非常光滑，这与文献［7］得到的结果是一致的.能量的二阶差分D2（En）和分裂能Delt（En）可以很好的反映团簇稳定性随尺寸的变化，从图中可以看到与Nin团簇一样，能量的二阶差分D2（En）和分裂能Delt（En）都没有表现出明显的奇偶振荡，这与过渡金属团簇的电子是非自由类的电子有关.n=4时两种方法得到的能量的二阶差分D2（En）和分裂能Delt（En）都有较大的峰值，说明n=4时的团簇较其它尺寸的团簇更稳定，在实验上更易获得.

图4 团簇平均结合能Eb 随团簇尺寸的演化Fig.4 Binding energy／atom Ebchanges with the size of clusters

3.4 磁性分析

一般来说团簇的磁距与所研究团簇的结构以及自旋多重度有密切的关系，定义团簇的自旋多重度（2S+1）与团簇（含有n 个原子）的平均每原子磁矩有以下的关系式μ=2SμB／n.在图7 中我们绘出了Pdn团簇的平均每原子磁矩随团簇尺寸的演化规律，其中包括文献［23］得到的理论结果.从图7可以看到，除n=3时，文献［23］和我们用BPW91方法得到的结果完全一致.除n=8，9外，文献［23］和我们用B3LYP 方法得到的结果相一致.文献［23］得到Pdn团簇的平均每原子磁矩随团簇尺寸逐渐减小，曲线非常光滑.两种方法得到的Pdn团簇的平均每原子磁矩随团簇尺寸总体有减小的趋势，但个别团簇有振荡.在n=3 时，BPW91方法得到了较大的磁矩，这与Pd3团簇的基态结构为近似直线的开环结构有关.在n=8，9时，B3LYP方法得到了较大的磁矩，B3LYP方法得到Pd9团簇两个能量几乎简并的基态结构为三戴帽八面体结构和两戴帽五角双锥结构，在计算磁矩时我们是按三戴帽八面体结构计算的，从而比BPW91方法和文献［23］大，说明团簇的构型对团簇的磁性的影响较大.

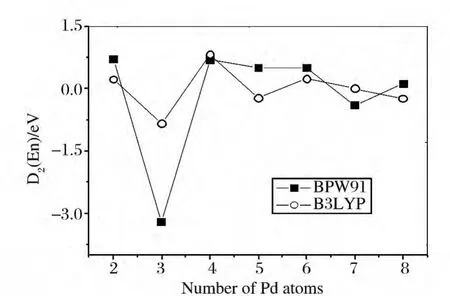
图5 团簇的能量的二阶差分D2（En）随团簇尺寸的演化Fig.5 Second difference in energy D2（En）changes with the size of clusters

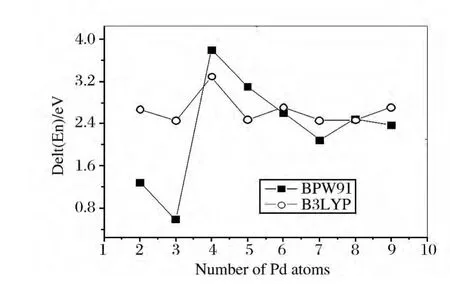
图6 团簇的分裂能Delt（En）随团簇尺寸的演化Fig.6 The first derivative of the total energy Delt（En）changes with the size of clusters

4 小 结

本文利用密度泛函理论系统地研究了Pdn（n=1～9）团簇的结构，稳定性和磁性.并比较了BPW91和B3LYP泛函下的计算结果.小结如下：

图7 团簇的平均每原子磁矩随团簇尺寸的演化Fig.7 The average magnetic moment／atomμBchanges with the size of clusters

（1）两种方法得到了完全相同的稳定结构，在n=3、4 两种方法得到的基态结构不相同.但三参数杂化密度泛函B3LYP 得到的基态结构的构型与文献［8，9，23］的完全相同，说明三参数杂化密度泛函B3LYP 对小的Pdn团簇的结构描述更精确.团簇的平均配位数和平均键长有相似的变化规律，总体上随团簇尺寸的增大而增大.

（2）两种方法得到的平均结合能都随团簇尺寸的增大而增大，团簇能量的二阶差分、分裂能在n=4 时均有较大的值，说明相对应的团簇具有较高的稳定性.

（3）对团簇磁性的研究表明团簇的平均每原子磁矩随团簇尺寸的增大有逐渐减小的趋势.

［1］ Meiyan N，Zhi Z.Density functional study of hydrogen adsorption and dissociation on small Pdn（n=1～7）clusters［J］.J.Mol.Struct.，2009，901：14.

［2］ Yan S Y，Jiang H，Yang Z Q，et al.Density functional theory study of small Nin（n≤8）clusters［J］.J.At.Mol.Phys.，2012，29（2）：281（in Chinese）［颜世英，江海，杨自钦，等.Nin（n≤8）团簇的密度泛函研究［J］.原子与分子物理学报，2012，29（2）：281］.

［3］ Ruan W，Xie A D，Yu X G，et al.Geometrical structures and electronic properties of Na3B3Hnclusters［J］.J.At.Mol.Phys.，2011，28（3）：175（in Chinese）［阮文，谢安东，余晓光，等.Na3B3Hn团簇的结构与电子特性 ［J］.原子与分子物理学报，2011，28（3）：175］.

［4］ Li J N，Pu M，Ma C C，et al.The effect of palladium clusters（Pdn，n=2～8）on mechanisms of acetylene hydrogenation：A DFT study［J］.J.Mol.Cata.A：Chem.，2012，359：14.

［5］ Wei L，Yao X Q，Tian X，et al.A DFT investigation of the effects of doped Pb atoms on Pdnclusters（13 ≤n≤116）［J］.Comp，Theo，Chem，，2011，966（1）：375.

［6］ Lacaze-Dufaure C，Roques J，Mijoule C，et al.A DFT study of the NO adsorption on Pdn（n=1～4）clusters［J］.J.Mol.Cata.A：Chem.，2011，341（2）：28.

［7］ Garcia R J，Rey C，Gallego L J，et al.Molecular-Dynamics study of the structures，binding energies，and melting of clusters of fcc transition and noble metals using the voter and chen version of the embedded-atom model［J］.Phys.Rev.B，1994，49，8495.

［8］ Irena E，Moshe S.Quantum chemical study of small palladium clusters［J］.Surf.Sci.，1998，414：148.

［9］ Karabacak M，Ozcelik S，Güvenc Z B.Structures and energetics of Pdn（n=2～20）clusters using an embedded atom model potential［J］.Surf.Sci.，2002，507：636.

［10］ Guo X Y.Formation and growth mechanism of Pdn clusters studied by the Monte Carlo method ［J］.Acta Phys.Chim.Sin.，2003，19（2）：174［郭向云.钯团簇形成和增长机理的Monte Carlo 研究［J］.物理化学学报，2003，19（2）：174］.

［11］ JoséR，Griselda G，Juan A V.Small Pd clusters：a comparison of phenomenological and ab initio approaches［J］.Phys.Rev.B，2005，72：115421.

［12］ Efremenko I，Sheintuch M.DFT study of small bimetallic palladium-copper clusters ［J］.Chem.Phys.Lett.，2005，401：232.

［13］ Reddy B V，Khanna S N，et al.Giant magnetic moments in 4dclusters［J］.Phys.Rev.Lett.，1993，70（21）：3323.

［14］ Douglass D C，Bucher J P，Bloomfield L A.Magnetic studies of free nonferromagnetic clusters［J］.Phys.Rev.B，1992，45：6341.

［15］ Kumar V，Kawazoe Y.Icosahedral growth，magnetic behavior，and adsorbate-induced metal-nonmetal transition in palladium clusters［J］.Phys.Rev.B，2002，66（14）：144413.

［16］ Shinohara T，Sato T，Taniyama T.Surface ferromagnetism of Pd fine particles ［J］.Phys.Rev.Lett.，2003，91：197201.

［17］ Wen J Q，Jiang Z Y，Li J Q，et al.Geometrical，electronic states，and stability of NinAl clusters.Int.J.Quan.Chem.，2010，110，1368.

［18］ Wen J Q，Jiang Z Y，Hou Y Q，et al.Geometrical structure，electronic states and stability of NinAl+clusters J.Mol.Struct.，2010，949：91.

［19］ Taniyama T，Ohta E，Sato T.Observation of 4d ferromagnetism in free-standing Pd fine particles［J］.Europhys.Lett.，1997，38：195.

［20］ Huber K P，Herzberg G.Constants of diatomic molecules［M］.New York：Van Nostrand Reinhold，1979，235.

［21］L in S S，Strauss B，Kant A.Dissociation energy of Pd2［J］.J.Chem.Phy.，1969，51：2282.

［22］ Ho J，Ervin K M，Polak M L.A study of the electronic structures of Pd-2and Pd2by photoelectron spectroscopy ［J］.J.Chem.Phy.，1991，95：4845.

［23］ Futschek T，Hafner J.Stable structure and magnetic isomers of small transition-metal clusters from the Ni group：an ab initio density-functional study［J］.J.Phys.：Condens.Matter.，2006，18：9703.