预紧工况下双锥环的有限元分析及优化

何家胜 黄瑞锋 伍 伟

（武汉工程大学机电工程学院)

设计与计算

预紧工况下双锥环的有限元分析及优化

何家胜*黄瑞锋 伍 伟

（武汉工程大学机电工程学院)

建立某加氢反应器双锥环结构的有限元模型，分析在预紧工况下，对双锥面施加一定的预紧分布压力后，双锥环结构的厚度与锥角对其径向压缩位移的影响。研究结果表明，该双锥环在预紧工况下能实现良好的密封，其径向压缩位移随厚度的增加而减小，随双锥环锥角的增大而增大。

双锥环 锥角 密封性能 有限元 径向位移 预紧工况

0 序言

双锥密封是一种半自紧密封形式，与仅依靠残余预紧力的常用法兰连接密封形式有较大差别，目前规范上仅仅给出了有限的几种规格参数。当实际工程中双锥密封的有关参数与规范中的参数不相对应时，就需要有效地调整参数，以保证密封效果。

本文主要探讨双锥密封的结构和密封原理，包括双锥环的材质、厚度、高度、锥角、直径、所受压力等因素对密封效果的影响。结合某炼厂加氢反应器双锥密封的具体情况，运用有限元数值分析方法求解预紧情况下双锥环垫片处的压紧力，双锥环的形变、应力，并探讨压力波动情况下垫片处压紧力的变化情况。图1所示为该双锥环的结构，其中试样材料为35钢，其弹性模量为212 000 MPa，泊松比为0.31，密封面预紧分布压力为60.7 MPa，设计压力为6.4 MPa。本文主要对内圆柱面直径（Di）为975 mm和1 171 mm的标准双锥环进行改进和研究。

1 双锥面的结构及受力分析

双锥环预紧状态下的受力分析如图2所示。在预紧状态下，应保证密封面上的软金属垫片达到初始密封的条件，同时应使双锥环产生径向位移以消除双锥环与平盖支撑面之间的径向间隙 （g）。

图1 双锥密封结构

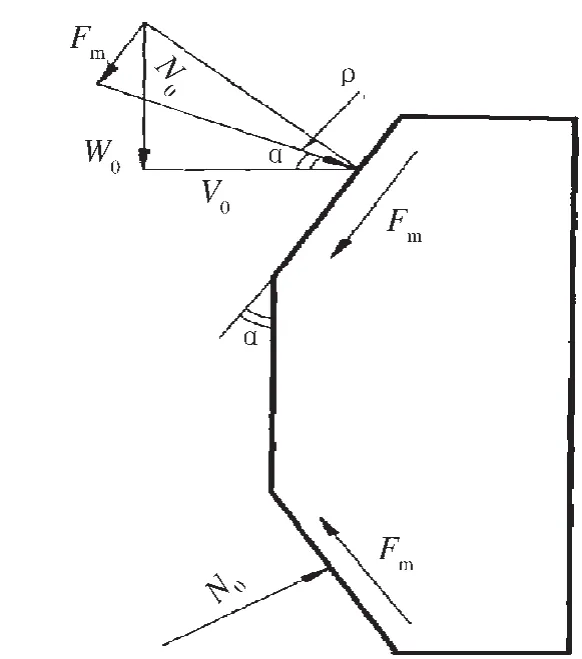
图2 预紧状态下双锥环受力分析

取软金属垫片为退火铝材料，查资料得其预紧密封比压 （y）为60.7 MPa，双锥面上所受的法向压紧力计算式为：

预紧时双锥环发生收缩变形，与平盖有相对滑动，双锥环受到摩擦力 （Fm）作用，摩擦力方向如图2所示，其计算式为：

而总螺栓预紧力 （W0）为Fm和双锥面所受的正压力 （N0）的合力在竖直方向上的分力，其计算式为：

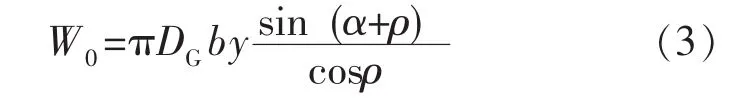
表1为根据式（1）～式（4）得出的标准状况下双锥环基本参数表。

2 有限元分析

2.1 模型建立

本文只对双锥环部分建立模型并进行分析。双锥环为轴对称结构，所以在ANSYS建模中可采用平面来表示空间轴对称模型，如图3、图4所示。

2.2 网格划分

双锥环模型网格划分如图5所示，共有5426个节点，1741个单元。

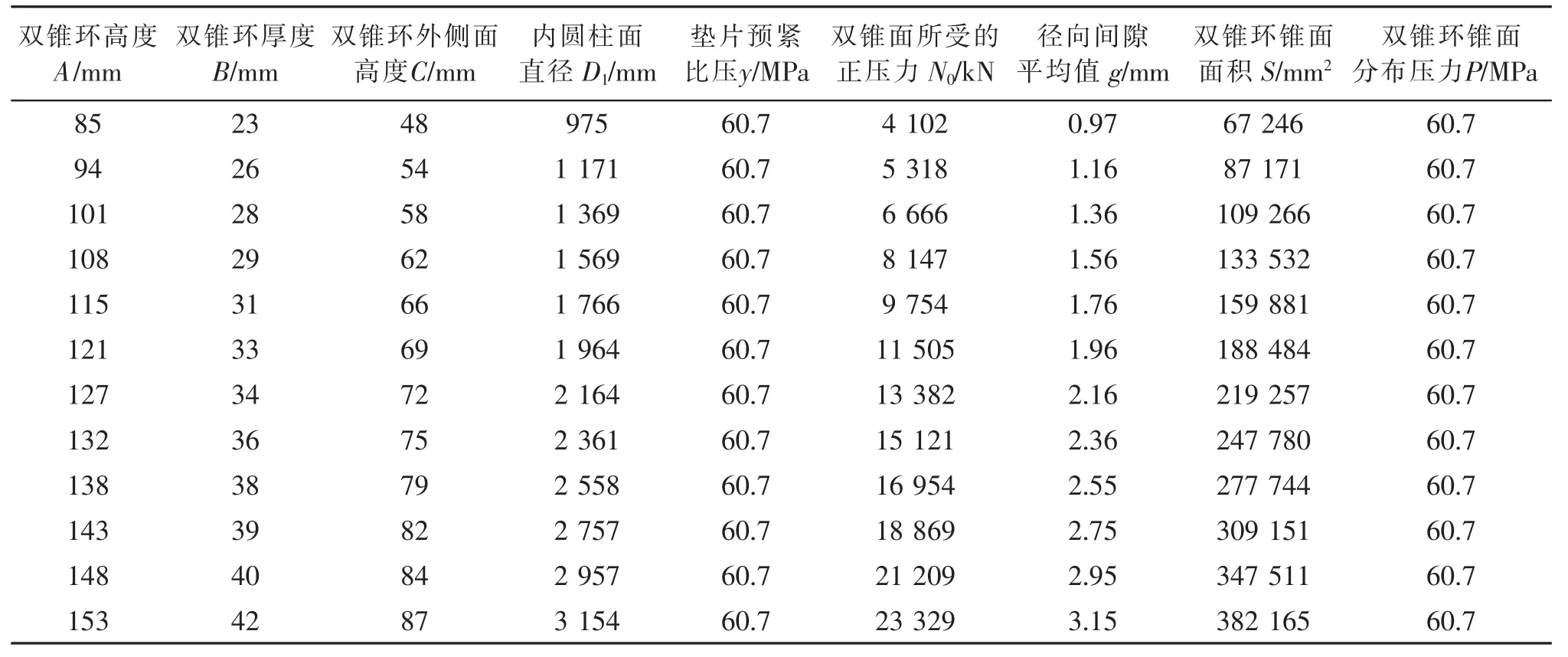
表1 双锥环基本参数

图3 平面空间轴对称模型

图4 双锥环三维模型

图5 双锥环模型网格划分

2.3 边界条件

模型中，需对上下锥面的法向方向进行约束，但因为该模型为空间轴对称模型，所以只需对该平面的斜边法向进行压力分布即可，如图6所示。由GB 150—2011《压力容器》查得双锥面的预紧分布压力为60.7 MPa。

3 结果分析

3.1 整体位移分布情况

在预紧分布压力的作用下，双锥环的整体位移分布如图7所示。由图7可见，双锥环位移分布并不均匀，最大位移出现在其内圆柱面的上下侧。

3.2 改变双锥环厚度对其径向位移的影响

图8～图10是在其他参数条件不变的情况下，仅仅改变双锥环厚度，其径向位移的云图比较。

图6 双锥环的边界条件

图7 双锥环整体位移分布情况

图8 厚度为23 mm标准双锥环径向位移分布云图

通过GB 150—2011可知，径向间隙g的取值范围为 （0.075%～0.125%）D1，对于内径D1为975 mm的双锥环，g取平均值为0.975 mm。而预紧时应保证密封面上的软金属垫片达到初始密封条件，应使双锥环产生径向弹性压缩以消除双锥环与平盖支撑面之间的径向间隙。

图9 厚度为23～26 mm的非标双锥环径向位移云图

图10 厚度为23～28 mm的非标双锥环径向位移云图

图8～图10的最大径向位移分别为1.45 mm、1.26 mm、1.16 mm，都大于 g（0.975 mm），所以设计是合理的，且径向压缩位移随着双锥环厚度的增加而逐渐减小。

为了能更清晰明了地反映双锥环厚度与径向位移的关系，可对4种不同内径下双锥环厚度与最大径向位移的变化曲线作一比较，如图11所示。

图11 不同内径下双锥环厚度与最大径向位移的关系

3.3 改变双锥环锥角对其径向位移的影响

图12～图13是在其他参数条件不变的情况下，仅仅改变双锥环锥角，对其径向位移影响的云图比较。 由双锥环截面形状可知， [（A-C）/2]tanα＜B，代入数据可得 α＜51.2°。由图8、图12和图13可知，锥角分别为30°、37.5°、45°时，径向位移分别为1.45 mm、1.53 mm、1.64 mm，即径向压缩位移随着双锥环锥角的增大而逐渐增大。

图12 厚度23 mm、锥角37.5°时双锥环径向位移云图

图13 厚度23 mm、锥角45°时双锥环径向位移云图

4 结论

（1）在预紧载荷作用下，该双锥环在一定范围内可以实现良好的密封。

（2）在其他条件不变的情况下，径向压缩位移随着双锥环厚度的增加而逐渐减小，随着双锥环锥角的增大而逐渐增大。

（3）在特殊工况下，可以在一定范围内改变标准双锥环的厚度和锥角来适应该特殊工况。

[1]余伟炜，高炳军.ANSYS在机械与化工装备中的应用[M].北京：水利水电出版社，2007.

[2]宗磊.双锥环密封系统的应用研究 [D].天津：天津大学，2014.

[3]高永建.大型高压容器双锥密封结构设计方法研究[D].杭州：浙江大学，2008.

[4]黄伟波，谢禹钧.加氢反应塔非标准双锥密封性能的有限元分析 [J].润滑与密封，2016，41（6）：102-105，124.

Finite Element Analysis and Optimization of Duplex Conical Rings under Pre-tightening Condition

He JiashengHuang RuifengWu Wei

A finite element model of duplex conical rings structure on a hydrogenation reactor was established.The influence of the thickness and conical angle of the duplex conical rings structure on its radial contraction was analyzed when a certain pre-tightening distribution pressure was applied to the duplex conical plane in the pre-tightening condition.The results showed that the duplex conical rings can achieve a good seal in the pretightening condition,and its radial shrinkage displacement decreased with the increase of thickness,and increased with the increase of the conical angle.

Duplex conical rings;Conical angle;Sealing performance;Finite element;Radial displacement;Pre-tightening condition

TQ 050.3

10.16759/j.cnki.issn.1007-7251.2017.08.002

2016-11-09）

*何家胜，男，1958年生，教授。武汉市，430200。