密度泛函理论研究Nin，Nin±（n=1～5）团簇的结构和电子性质

张 蓓，刘东东，陈 楚，张 军

（新疆大学物理科学与技术学院，乌鲁木齐830046）

1 引 言

近年来，团簇凭借其独特的物理化学性质在催化、磁性、光谱学等领域的重要应用价值已引起了理论和实验方面的广泛关注与研究［1］.基于团簇的量子尺寸效应，添加或者删除一个原子都会使团簇的基态几何结构和性质发生很大的变化［2］，进而我们认为：在中性团簇的基础上添加或除去一个电子对其几何结构以及电子结构特性也会产生较大的影响.在实验中制备团簇主要方法有［2］：溅射法，化学气相沉积法，激光蒸发法等.其中有些方法是在高温或者高能的环境下进行，因而生成的团簇极有可能是带电体系，系统计算和研究带电团簇的电子结构特性是具有实验基础和研究意义的［3］.

人们采用各种计算模拟方法对单质金属团簇进行了大量的研究［4-10］.镍（Ni）作为3d族过渡金属元素，在电子和催化等领域有极大的应用价值，已经受到理论学家和实验家们极大的关注，但主要还是局限在对中性镍团簇的研究：孙厚谦［11］等人采用经验势和遗传算法（Genetic Algorithm）计算了Nin（n=2～20）团簇的平衡结构和束缚能，并将计算结果与基于第一性原理讨论的数据进行比较；Y.Xiang［12］等采用模拟退火算法系统研究了Nin（n=2～55）团簇的几何结构特性，发现13，38，55 是他们所讨论的团簇体系中的幻数；Miguel Castro［13］等人采用局域Generalized gradient approximations（GGA）下的全电子密度泛函理论模拟计算了小尺寸Fen，Con，Nin（n≤5）团簇的磁矩，自旋极化等电子结构特性.而近期，阎世英以及朱正和［14］等人采用高斯程序的B3LYP 交换关联函数优化计算了Nin（n≤8）团簇体系的键能以及离化能等相关性质.

本文采用广义梯度近似（GGA）的密度泛函理论系统研究了Nin，Ni±n（n=1～5）团簇的几何结构和电子结构特性.基态的几何结构，对称性，最高占据轨道与最低未占据轨道能隙（the HOMOLUMO energy gaps），磁矩以及绝热电子亲和能等物理性质在文中都进行了系统的讨论，并将计算结果与已有的理论［14］及实验结果进行比较.

2 计算方法

采用Quantum-ESPRESSO 软 件 包［15，16］，并选用Vanderbilt模式的超软赝势计算离子核与价电子之间的相互作用势，本次计算均是在梯度近似的密度泛函理论框架下运行，其中波动方程以30ry 的运动能量为一组的平面波矢下展开.PWscf软件提供了多种类型的交换关联势，包括LDA 势和GGA 势，本次工作中交换关联作用在广义梯度近似下的PBE［17］方程中进行处理.为避免团簇间的相互作用，我们根据团簇体系的大小，设定晶胞的尺寸为12Å～16Å 不等.

所有原子不受任何限制采用Broyden-Fletcher-Goldfarb-Shanno（BFGS）算法进行驰豫.对于团簇的初始构型，根据结构的对称性从一维到三维都列入考虑范围，没有对称性的几何结构我们也进行了计算.收敛标准为：原子间平均作用力为0.01eV／Å 以及团簇与上一代个体的能量差的绝对值达到10-6ryd.

3 结果与讨论

3.1 Nin+ ，Nin，Nin- （n=1～5）团簇的基态几何结构

如图1所示：Ni+2为具有Dh对称性的哑铃线性结构，Ni+3为平面等边三角形，对称性为D3h；Ni+4体系呈现正四面体构型，其对称性为Td；Ni+5为三角双锥构型，呈D3h对称性，将正电体系的研究结果与阎世英［14］等人的工作进行比较符合得非常好.对于中性的Nin（n=1～5）团簇，基态几何结构与相应尺寸的正电体系基本一致，除Ni5，其基态几何结构为等边四角单锥结构，呈C4v对称性.将中性Nin（n=1～5）团簇的计算结果与已有的实验及理论计算数据进行比较，列在表1 中.

结合表1的数据我们可以看到，n=2～4，我们的计算结果与Reuse［19］等人（采用基于密度泛函理论的ab initio 从头计算法）的计算结果以及实验数据符合得很好，并且找到了更低的结合能.到n=5时，Reuse［19］认为Ni5团簇的基态几何构型是具有D3h对称性的三角双锥结构（Eb=2.83 eV），而我们的计算结果表明四角单锥结构才是Ni5团簇的基态几何构型（Eb=2.84eV ＞2.83eV，C4v），可见本次计算我们所采用的计算方法更有利于找到Ni小团簇的基态几何构型.

表1 Nin（n=2～5）团簇的对称性（Sym），平均结合能（Eb）以及磁矩（M），结合已有的理论值及实验数据进行比较 Table 1 Symmetry（Sym），average binding energies（Eb）and magnetic moments（M）of Nin（n=2～5）clusters，compared with experimental data and theoretical values

注：a：Ref.［18］，b：Ref.［13］，c：Ref.［19］，d：Ref.［20］，expt：Ref.［20］

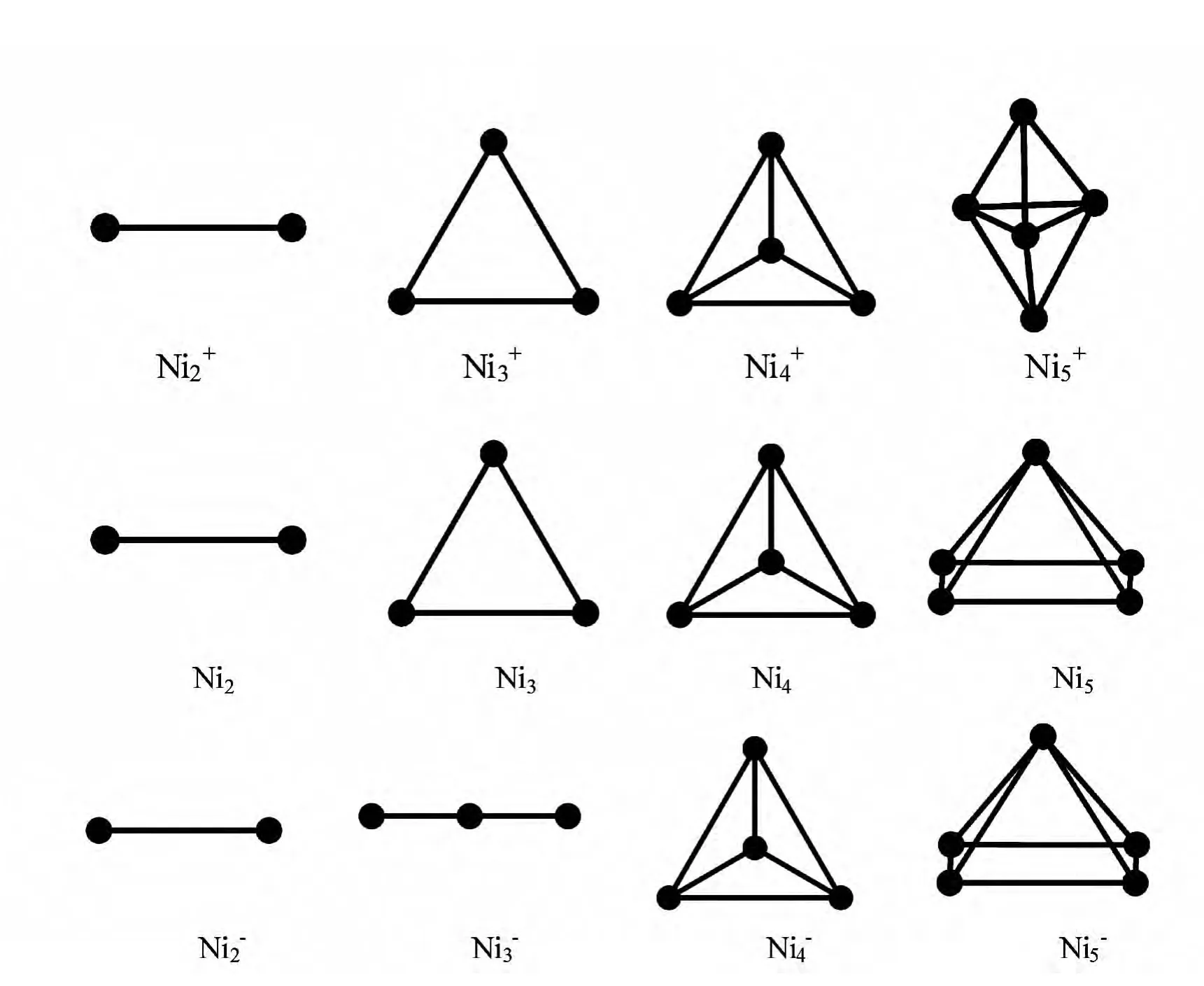
图1 Ni+n ，Nin，Ni-n （n=1～5）团簇的基态几何结构图Fig.1 The ground state structures of Ni+n ，Nin，Ni-n （n=1～5）clusters

负电体系，Ni-2依旧为哑铃型线性结构，其结合能为2.68eV，与Weber［20］的工作（Eb（Ni-2）=2.62eV）符合得非常好；Ni-3与Ni3及Ni+3的基态几何构型明显不同，是具有D3h对称性的一维线形结构；Ni-4，Ni-5团簇的基态几何构型与相应的中性团簇 相 同，这 与 阎 世 英［14］（Ni-5：C2v，pyramidal）等人的讨论一致.从图1可以明显看出：随着原子数目的递增，正电体系的基态几何结构与中性个体之间的差异逐渐表现出来，而带负电的体系则表现不明显.

综上所述，我们可以发现对于我们所讨论的体系，随着团簇尺寸的增加，团簇的构型有从平面转向立体的总体趋势.对中性Nin（n=1～5）团簇除去一个电子对基态几何结构所引起的变化相比增加一个电子所引起的影响要更为明显.

3.2 Nin+ ，Nin，Nin- （n=1～5）团簇的电子结构特性

最高占据轨道与最低未占据轨道能隙是体现团簇的化学活性具有代表意义的物理量，能隙越大则化学活性越低，其结构也就可能越稳定；反之，能隙越小则化学活性越高，其相应结构也就越不稳定.因此HOMO-LUMO 能隙能够间接反应团簇体系的结构稳定性.

图2 给出的是Ni+n，Nin，Ni-n（n=1～5）团簇的HOMO-LUMO 能隙图.由图我们可以看到：对于中性和带负电的Nin（n=1～5）团簇体系，其HOMO-LUMO 能隙存在明显的奇偶振荡；到n=4时，Ni+4、Ni4和Ni-4团簇体系明显大于与其邻近的团簇体系的能隙值，说明具有较低的化学活性.为进一步确定幻数结构，我们计算了Ni+n，Nin，Ni-n（n=1～5）团簇的二阶差分能（Δ2E），具体表达式为：

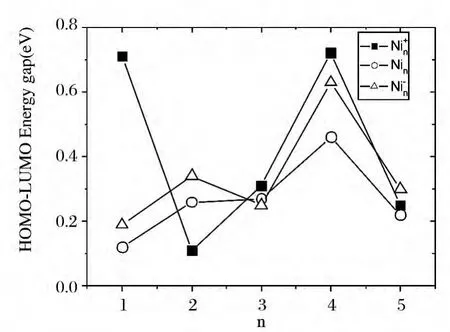
图2 Ni+n ，Nin，Ni-n （n=1～5）团簇最高占据轨道与最低未占据轨道能隙图Fig.2 HOMO-LUMO energy gaps（eV））of Ni+n ，Nin，Ni-n （n=1～5）clusters

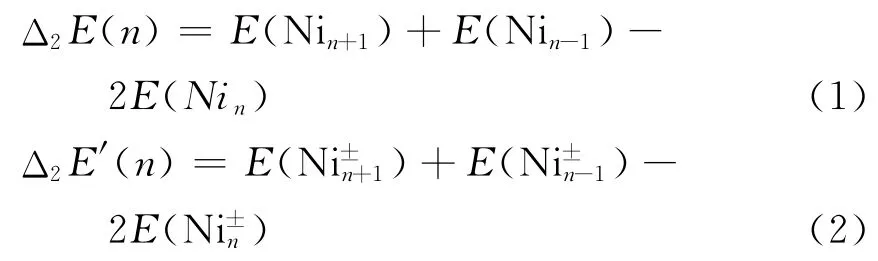
其中E 代表相应尺寸团簇的总能.计算结果汇总于表2，在本文所讨论的尺寸范围内我们没有找到幻数团簇，这与Saroj K［18］等人的结论完全一致.

表2 Ni+n ，Nin，Ni-n （n=1～5）团簇的二阶差分能（Δ2E）Table 2 The second order energy differences（Δ2E）of Ni+n ，Nin，Ni-n （n=1～5）clusters

图3给出的是Ni+n，Nin，Ni-n（n=1～5）团簇随尺寸递增的磁矩变化曲线.由图我们发现：n≤3时，Ni+n体系的磁矩是大于中性团簇的，但到n≥4时，正电体系的磁矩曲线位于中性体系的下方；而Ni-n（n=1～5）团簇体系的磁矩曲线始终位于中性体系的上方.可见：对比中性的Nin（n=1～5）团簇，添加一个电子能够增强体系的磁性.在我们所讨论的尺寸范围内，Ni+n，Nin，Ni-n（n=1～5）团簇体系随所含原子数的增多，磁矩整体呈现上升的趋势.

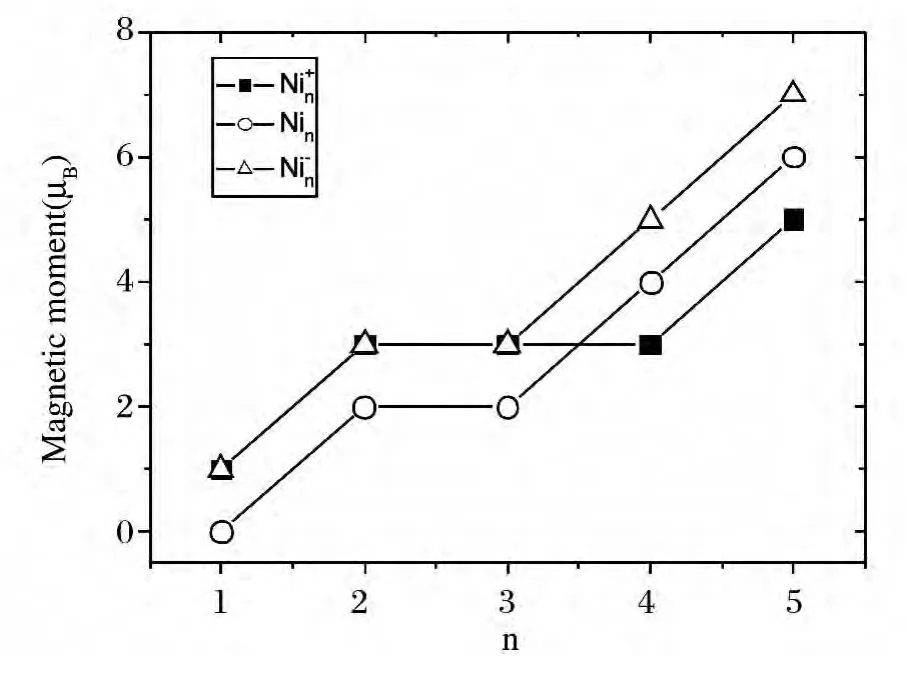
图3 Ni+n ，Nin，Ni-n （n=1～5）团簇的磁矩（Magnetization（μB））Fig.3 Magnetic moments ofNi+n ，Nin，Ni-n （n=1～5）clusters

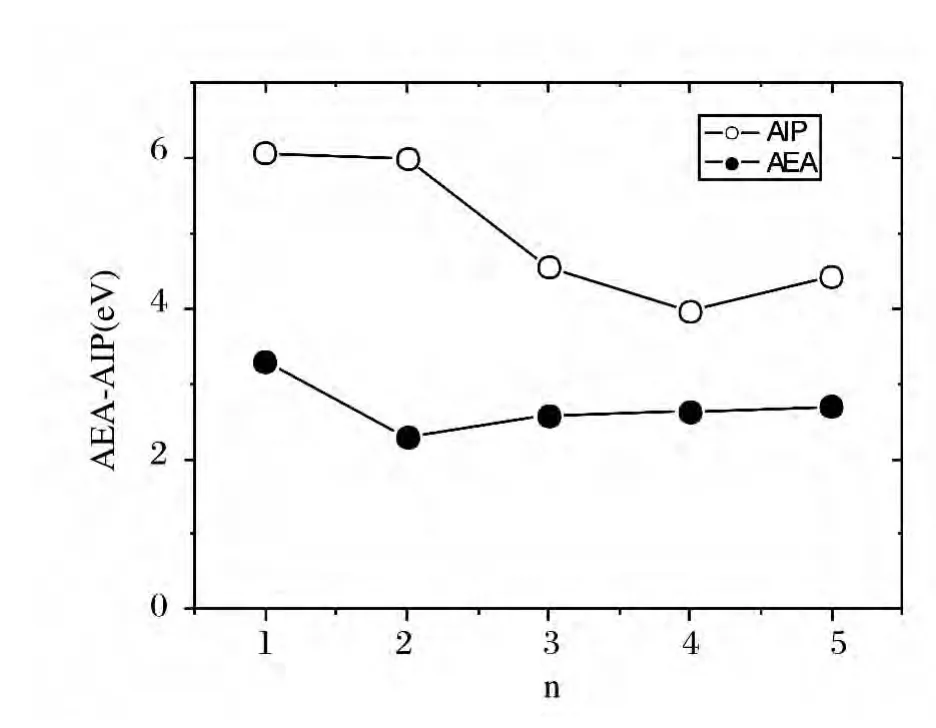
图4 Ni+n ，Nin，Ni-n （n=1～5）团簇的绝热电子亲和能（AEAs）及绝热离化能（AIPs）（eV）Fig.4 Adiabtic electronic affinities and adiabic ionization potentials of Ni+n ，Nin，Ni-n （n=1～5）clusters

图4绘出的是Ni+n，Nin，Ni-n（n=1～5）团簇的 绝 热 电 子 亲 和 能（adiabatic electronic affinites AEAs）及绝热离化能（adiabatic ionization potentials AIPs）图.其分别对应相同尺寸的带正电（带负电）团簇基态几何结构与中性团簇基态几何结构的总能差.液滴模型实验中提到：单质金属团簇（Fe）的EAs随原子数的增大而增大，而IPs则随着原子数的增大而减小，伴随着团簇尺寸的递增，他们在宏观极限下均趋向于功函数值［21］.图4 显示：单质Ni团簇的AIPs以及AEAs曲线的变化趋势完全符合液滴模型实验，并且绝热电子离化势（AIPs）始终位于绝热电子亲和能（AEAs）的上方.Ni小团簇的绝热电子亲和能和绝热电离势随尺寸变化波动较大，这是由于：对于小尺寸的团簇而言，得失一个电子，对其几何结构以及其他相关性质的影响是不可忽视的.依据图4中曲线的变化趋势我们可以推测：随尺寸的增加单质Ni团簇的AEAs和AIPs变化将趋于一致，这和实验模型中的纯金属（Fe，Co）团簇是相同的.

4 结 论

本文采用基于密度泛函理论的第一性原理对中性及带电的Ni小团簇进行了系统研究，发现随着团簇尺寸的增加，Ni+n，Nin，Ni-n（n=1～5）团簇的基态几何结构整体呈现从线形到立体，低维到高维的转化趋势；对比中性个体的几何结构，除去一个电子后，Ni+5的基态结构呈三角双锥构型，明显不同于中性及带负电的个体（Ni5，Ni-5：四角单锥构型），可见对中性团簇Nin（n=1～5），除去一个电子对基态几何结构所引起的变化相比增加一个电子所引起的影响要更为明显.

讨论Ni+n，Nin，Ni-n（n=1～5）团 簇 的HOMO-LUMO 能隙以及二阶差分能（Δ2E），发现Ni+4、Ni4和Ni-4的能隙值明显大于其邻近个体，具有较低的化学活性，但在我们所讨论的尺寸范围内，没有找到幻数结构.Ni+n，Nin，Ni-n（n=1～5）团簇的磁矩（Magnetization（μB ））整体呈现上升趋势，添加一个电子会显著增强个体的磁性.Nin（n=1～5）团簇的绝热电子亲和能（AEAs）及绝热离化能（AIPs）曲线波动较大，可见对于小尺寸的团簇体系，添加或除去一个电子对其几何结构以及其他相关性质的影响都是不可忽视的.分析曲线的变化趋势，我们推测：随着原子个数的增加，AEAs和AIPs两条曲线有可能趋于一致.

［1］ Li S，Alemany M G，Chelikowsky J R.Real space pseudopotential calculations for copper clusters［J］.Chem.Phys.，2006，125：034311.

［2］ Wang G H.Cluster physics［M］.Shanghai：Shanghai Scientific and Technology Press，2003（in Chinese）［王广厚.团簇物理学［M］.上海：上海科学技术出版社，2003］

［3］ Zhang B，Chen C，Zhang J.Density-functional calculations of Co+n，Con，Co-n（n=1～5）clusters［J］.J.At.Mol.Phys.，2011，28（5）：875（in Chinese）［张蓓，陈楚，张军.Co+n，Con，Co-n（n=1～5）团簇的密度泛函理论研究［J］.原子与分子物理学报，2011，28（5）：875］

［4］ Tian W D.The study of the stability and electronic structure of the icosahedral Sc13，Sc13+1and Sc13-1clusters［J］.J.At.Mol.Phys.，2009，26（4）：501（in Chinese）［田维钊.二十面体Sc13，Sc13+1，Sc13-1团簇的稳定性与电子结构研究［J］.原子与分子物理学报，2009，26（4）：501］

［5］ Knickelbein M B.Electronic shell structure in the ionization potentials of copper clusters［J］.Chem.Phys.Lett.，1992，192：129.

［6］ Kuang X J，Wang X Q，Liu G B.Calculations on the geometrical structure，electronic and magnetic properties of Rh13cluster［J］.J.At.Mol.Phys.2010，27（2）：253（in Chinese）［邝向军，王新强，刘高斌.Rh13团簇的几何结构和电子与磁性性质的计算［J］.原子与分子物理学报，2010，27（2）：253］

［7］ Itoh M，Kumar V，Adschiri T，et al.Comprehensive study of sodium，copper，and silver clusters over a wide range of sizes 2 ≤N ≤75［J］.J.Chem.Phys.，2009，131：174510.

［8］ Oviedo J，Palmer R E.Amorphous structures of Cu，Ag，and Au nanoclusters from first principles calculations［J］.J.Chem.Phys.，2002，117：9548.

［9］ Dieguez O，Alemany M M G，Rey C，Ordejon P，et al.Density-functional calculations of the structures，binding energies，and magnetic moments of Fe clusters with 2to 17atoms［J］.Phys.Rev.B.2001，63：205407.

［10］ Duan H M，Zheng Q Q.Symmetry and magnetic properties of transition metal clusters［J］.Phy.Lett.A，2001，280：333.

［11］ Sun H Q，Ren Y，Wang G H.Equilibrium geometries of Nin（n=2～20）clusters［J］.J.At.Mol.Phys.，2001，18（4）：387（in Chinese）［孙厚谦，任云，王广厚，Nin（n=2～20）团簇的结构［J］.原子与分子物理学报，2001，18（4）：387］

［12］ Xiang Y，Sun D Y，Gong X G.Generalized simulated annealing studies on structures and properties of Nin（n=2～55）clusters［J］.J.Phys.Chem.A，2000，104：2746.

［13］ Miguel C，Christine J，Dennis R S.Structure，bonding，and magnetism of small Fen，Conand Ninclusters，n≤5［J］.Chemical Physics Letters.，1997，271：133.

［14］ Yan S Y，Jiang H，Yang Z Q，et al.Density functional theory of small Nin（n≤8）clusters［J］.J.At.Mol.Phys.，2012，29（2）：281（in English）［阎世英，江海，杨自钦，等.Nin（n≤8）团簇的密度泛函研究［J］.原子与分子物理学报，2012，29（2）：281］

［15］ Zhang Z X，Cao B B，Duan H M.Density-functional calculations of MnC（M=Fe，Co，Ni，Cu，n=1～6）clusters［J］.J Mol Struc（Theochem），2008，863：22.

［16］ Baroni S，Corso A D.Available from＜http：／／www.pwscf.org＞.

［17］ Perdew J P，Burke K，Ernzerhof M.Generalized gradient approximation made simple［J］.Chem.Phys.Lett.，1996，77：3865.

［18］ Nayak S K，Khanna S N，Rao B K，et al.Physics of nickel clusters：energetics and equilibrium geometries［J］.J.Phys.Chem.A，1997，101：1072.

［19］ Reuse F A，Khanna S N.Geometry electronic structure，and magnetism of small Nin（n=2～6，8，13）clusters［J］.Chemical Physics Letters.，1995，234：77.

［20］ Weber S E，Jena P.Isomerism of Ni cluster anions and its role on photo-detachment spectroscopy［J］.Chemical Physics Letters.，1997，281：401.

［21］ Zhang B，Bao A，Chen C，et al.Density-functional theory study of ConCm±（n=1～5，m=1，2）clusters［J］.Acta Phys.Sin.，2012，61（15）：153601（in Chinese）［张蓓，保安，陈楚，等.ConCm±（n=1～5，m=1，2）团簇的密度泛函理论研究［J］.物理学报2012，61（15）：153601］