AlH+离子A2∏态势能函数的变分研究
2014-05-29刘国跃廖碧涛
刘国跃,廖碧涛,吴 英
(1.绵阳师院计算物理研究中心,绵阳621000;2.绵阳师院物理与电子工程学院,绵阳621000)
1 引 言
双原子分子离子的正确势能行为一直是原子与分子物理的重要研究课题,在大气化学、星云介质、溶液化学、等离子体等研究中起着非常重要的作用[1].比如,离子的势能行为可以有效地影响基于离子蒸汽的激光泵浦的效率,影响原子与离子间的低能散射截面和分子离子的结构研究等,航空航天技术、激光技术、等离子体技术的发展等也迫切需要分子离子的大量数据[2-4].实验测量分子离子XY+的势能数据会随振动量子数升高而越来越困难,在重要的离解区和渐进区常常缺乏测量结果.量子力学从头计算是研究双原子分子离子XY+的势能行为的重要方法之一,相关的成果报道较多[5,6].但是,有些量子力学从头计算对原子实极化等重要物理效应处理不够理想,有的计算选用的基函数和截断点尝试性居多物理意义并不很明确等,结果的准确性有时不是很高[7,8].从头计算方法的结果是数值解,有时不能满足象碰撞研究这类问题的需要,全程解析势能函数仍然具有不可替代的作用.
铝化物及其离子由于固体推进器和爆破中的应用,几十年来一直受到人们的关注[9],1979年,L.B.Knight等人研究了AlH+自由基离子产生的有关化学反应[10],1982年,Ramsay等人采用红外吸收光谱技术获得了AlH+离子基态和低激发态的振转光谱[11],1984年,Balfour等人采用气相摄谱技术研究了AlH+离子基态X2∑+和低激发态 A2∏、C2∑+的振转光谱[12],直到2011年,相关的研究仍有报道,Szajna等人都还在对AlH+离子基态X2∑+和低激发态A2∏进行光谱研究[13];Nguyen等人采用量子力学从头计算研究了AlH+离子基态X2∑+和低激发态A2∏之间能级跃迁的光谱[14].但是,关于AlH+离子基态X2∑+和低激发态A2∏的势能数据却很缺乏,更没有给出全程解析的势能函数.本文采用研究双原子分子离子XY+势能函数的能量自洽法(Energy-consistentmethod for ion XY+,ECMI)研究了氢化铝离子AlH+激发态A2∏的解析势能函数.第二部分是对该方法的描述,第三部分是对氢化铝离子AlH+激发态A2∏的具体应用,结论和讨论放在第四部分.
2 双原子分子离子XY+的ECMI势和ECMI方法
带电的双原子分子离子XY+的电子结构与中性双原子分子有所不同.中性双原子分子失去一个电子就形成了双原子分子离子XY+,电荷量的改变必然导致电子云的重新分布,电子之间、电子与核之间的相互作用随之发生了变化,原来中性双原子分子的Hamilton量中的Coulomb项发生了变化,原子实的极化、电子运动的总角动量、自旋与轨道耦合的情况等都会随之改变.因此,带电的双原子分子离子XY+与中性双原子分子的解析势能函数是不同的,若采用中性分子的势能函数,例如Morse 势[15]和 Huxley-Murrell-Sorbie(HMS)势[16,17]等来描述带电的双原子分子离子 XY+的势能行为,有时会产生较大偏差甚至错误[18,19],应采用基于变分的双原子分子离子XY+的能量自洽法(Energy-consistent-method for ion XY+,ECMI)ECMI研究双原子分子离子XY+的解析势能函数ECMI势.
构建双原子分子离子XY+解析势能函数Uion(R)的基本物理思想就是在中性双原子分子XY的势能函数Umol(R)的基础上加上变分可调的Coulomb修正项L(R)/R,考虑电子状态改变造成的能量变化,双原子分子离子XY+解析势能函数ECMI势具有下面的一般形式
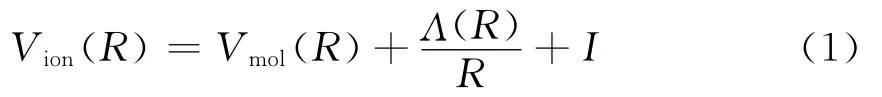
这里,I是离化势,如果选择将势井底部放在水平轴上,该常数可以从上述方程中舍去.
Vmol(R)是中性双原子分子的势能函数,它是双原子分子离子XY+的ECMI势的主体,它的解析形式与HMS势相同,但要用孙卫国和冯灏用二阶微扰理论的结果通过光谱数据求得三阶和四阶力常数[20]
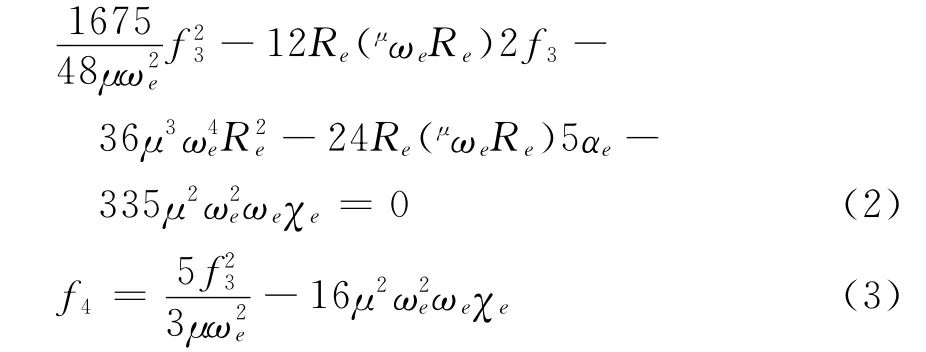
再按照Huxleyh和Murrell提出的方案用如下的方程来确定展开系数[19]
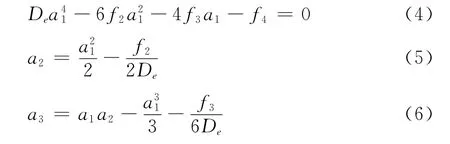
如此确定的HMS势称为MHMS势UMHMS(R)
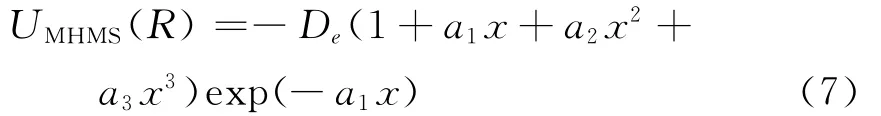
变分可调的Coulomb修正项的确定是困难的.首先,修正项L(R)/R必须在平衡核间距有极小值,即一阶导数等于零;其次,修正项必须有良好渐近行为,且当核间距R很大时,修正项的值要趋于零;不能产生物理上不存在的拐点和错误发展趋势,并对中性分子势能函数MHMS势可能产生的不足或不准确行为具有校正作用.下面的Coulomb变分修正项满足了这些要求[18]
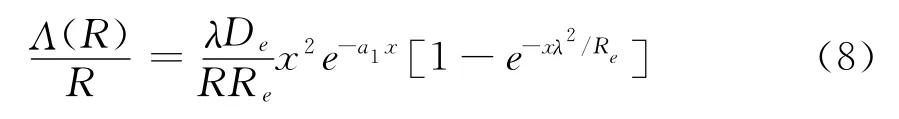
这里的λ是变分参数,要采用能量自洽法ECMI来确定.能量自洽法ECM是由孙卫国在1997年提出的根据能量自洽确定中性双原子势能函数中变分参数的方法[20,21],后来被改进和推广成为双原子分子离子XY+的能量自洽法ECMI[18],主要步骤是:
1)采用给定状态下的双原子分子离子XY+的一组基本数据(De,Re,ωe,ωeχe,αe),按照谐振子模型求出二阶力常数f2,根据方程(2)和(3)求出三阶和四阶力常数f3和f4,再由方程(4)~(6)求得MHMS势的展开系数{an},从而确定了势能函数的主体MHMS势.
2)给变分参数λ一个初始值,就给出了双原子分子离子XY+的一个尝试解Vion(R,λ),将其带入径向薛定谔方程(RSE),运用重归一的Numerov方法求解,就得到了双原子分子离子XY+在该电子状态下的一组振动能级{Gv}.
3)将计算得到的振动能级Gv与实验或精确理论得到的“真实”振动能级G’v进行比较.
4)如果求出的能级没有收敛于“真实”能级,则调整变分参数λ,重复步骤(2)和(3),直到求出的能级收敛于“真实”能级,即|Gv-G’v|小于要求的精度,这时相应的λ就是所确定的变分参数值,双原子分子离子XY+的势能函数也就完全确定了,并称为ECMI势.
3 AlH+激发态A2∏的ECMI势
采用双原子分子离子XY+的能量自洽法ECMI研究了AlH+激发态A2∏的解析势能函数ECMI势.研究中,采用了原子单位,Eh=1Hartree=219,474.63067cm-1,a0=0.0529176719 nm.基本数据(De,Re,ωe,ωeχe,αe)、求出的力常数{fn}、展开系数{an}和最后确定的变分参数λ均列在表1中.

表1 AlH+离子激发态A2∏的基本数据、求出的力常数、展开系数和变分参数Table 1 Molecular ionic constants,force constants,expansion coefficients and variationalparameter for the exited state A2∏of AlH+
图1是AlH+离子激发态A2∏的势能曲线,为了便于比较,采用Le Roy R J在文献[22]中提到并公布的程序计算出来的RKR数据(〇).Chien-Yu Lien等人采用MCSCF方法,分析了离解能和势能行为,计算出的离解能明显低于实验数据,本文借用了给出的势能数据(*)[13].由图可见,这三种不同的势能函数都很好描述了平衡核间距(Re=2.3506a0)附近的势能行为,与基于实验的RKR数据符合得很好.但从偏离平衡核间距不远约的R=3.6a0开始,Morse势(---)和 HMS势(-· -)就开始低于RKR数据,并且随着核间距的增加,差距越来越明显,在离解区这样的差异最大,HMS势向离解极限收敛比Morse势更慢;在给出的MCSCF数据范围内,直到R=5.0a0,MCSCF数据与Morse势是重合的,但核间距大于5.0a0时,MCSCF数据比Morse势和HMS势更低,表现出明显低于正确离解极限的收敛行为,并且给出的数据非常有限,不能满足许多研究的需要;而只有ECMI势(——)一直与RKR数据符合得很好,并给出了全程的势能数据,所以本文研究的全程解析势能函数的确非常必要.
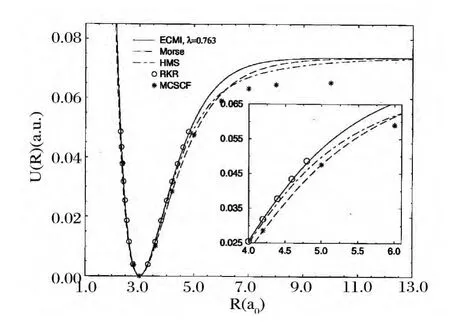
图1 氢化铝离子AlH+激发态A2∏的势能曲线.〇代表RKR数据,﹡代表 MCSCF方法的数据,---代表 Morse势,-· -代表 HMS势,——代表ECMI势,变分参数λ=0.763Fig.1 Potential energy curves(PEC)for the electronic state A2∏of AlH+ion.RKR data(〇),MCSCF data(﹡),the HMS potential(-·-),the Morse potential(- --),ECMI potential(——)withλ=0.763
4 结 语
本研究的结果表明,采用中性分子势能函数描述氢化铝离子AlH+激发态A2∏的势能行为在平衡核间距附近几乎是等价的,但随着核间距的增大,会表现出不同程度的误差.双原子分子离子XY+的能量自洽法ECMI是研究氢化铝离子AlH+激发态A2∏的势能行为的好方法,得到的AlH+离子激发态A2∏态的全程解析势能函数优于中性分子的Morse势和HMS势对该分子离子激发态势能行为的描述.在渐近区和离解区,势能数据对散射问题等不少研究非常重要和必须,而基于实验的RKR数据却没有;理论方法MCSCF的数据也不完备,并且预计的离解极限与实验结果差异明显,只有ECMI势给出了氢化铝离子AlH+激发态A2∏正确的全程势能数据和正确的理解极限,这对相关研究是必须的.
[1]Haridass C,Prasad C V V,Reddy S P.The comettail(A2Pi-X2S+)System of12C16O+:a reinvestigation[J].J.Mol.Spectrosc.,2000,199,180.
[2]Bellomonte L,Cavaliere P,Ferrante G.Alkali molecular ion energies and expectation values in a model-potential treatment[J].J.Chem.Phys.,1974,61,3215.
[3]Bardsley J N,Junker B R,Norcross D W,Pseudopotential calculations for Na2+,Na and Na2[J].Chem.Phys.Lett.,1976,37:502.
[4]Magnier S,Mollie P,Dulieu O,et al.Potential curves for the ground and excited states of the Na2molecule up to the(3s+5p)dissociation limit:results of two different effective potential calculations[J].J.Chem.Phys.,1993,98,7113.
[5]Bowler D R,Bush I J,Gillan M J.Practical methods for ab initio calculations on thousands of atoms[J].Int.J.Quantum.Chem.,2000,77:831.
[6]Cai Z L,Francois J P.Electronic sbsorption spectra of SiC-anion[J].J.Phys.Chem.,1997,A103:275.
[7]Müller W,Meyer W.Ground-state properties of alkali dimers and their cations(including the elements Li,Na,K)fromab initio calculations with effective core polarization potentials[J].J.Chem.Phys.,1984,80:3311.
[8]Sunil K K,lin J,siddiqui H,Siska P E,et al,theoreatical investigation of the a3a3∑+u,A1∑+u,c3∑+gand c1∑+gpotential energy curves of He2and He*(21S,23S)+ He scattering[J].J.Chem.Phys.,1983,78:6190.
[9]Lien C Y,Williams S R,Odom B.Optical pulse-shaping for internal cooling of molecules [J].Phys.Chem.Chem.Phys.,2011,13:18825.
[10]Knight L B,Martin R L,Davidson E R.ERS matrix isolation investigation of aluminum hydride radical cation-AlH+[J].J.Chem.Phys.,1979,71:3991.
[11]Ramsay D A,Sarre P J.High-resolution study of the A2P- X2S+band[J].J.Chem.Soc.Faraday Trans.Ⅱ,1982,78:1331.
[12]Balfour W J and Lindgren B,The A2Π-X2∑+system of AlD+and the C1∑-A1Πsystem of AlD[J].J.Phys.B:At.Mol.Phys.,1984,17 L861.
[13]Szajan W,Zachwieja M.High-resolution emission spectroscopy of A2P- X2S+system of AlH+[J].J.Mol.Spectroscopy.,2011,269:56.
[14]Nguyen J H V,Viteri C R,Hohenstein E G,et.al,Chllenges of laser-cooling molecular ions [J].New Journal of Phys.,2011,13:063023(http://www.njp.org).
[15]Morse P M.Diatomic molecules according to the wavemechanics.Ⅱ.Vibrational levels[J].Phys.Rev.,1929,34:57.
[16]Murrell J N,Sorbie K S.New analytic form for the potential energy curves of stable diatomic states[J].J.Chem.Soc.Faraday Trans.Ⅱ,1974 70:1552.
[17]Huxley P,Murrell J N.Ground-state diatomic potentials[J].J.Chem.Soc.Faraday Trans.Ⅱ,1983 79:323.
[18]Liu G Y,Sun W G,Feng H.Studies on the analytical energy function of diatomic molecular ion XY+using variational method[J].Science in China Ser.G,2004 47:154.
[19]Liu G Y,Sun W G,Feng H.The analytical potential energy function of groung state of halogen hydrogen ion HX+(X=F,Cl,Br,I)using the ion energy consistent method(ECMI)[J].J.At.Mol.Phys.,2007,24:57(in Chinese)[刘国跃,孙卫国,冯灏.用双原子分子离子XY+的能量自洽发研究卤化氢离子 HX+(X=F,Cl,Br,I)基态的势能函数[J].原子与分子物理学报,2007,24:57]
[20]Sun W G,Feng H.An energy consistent method for potential energy curves of diatomic molecules[J].J.Phys.B.,1999,32:5109.
[21]Sun W G.The energy-consistent method for the potential energy curves and the vibrational eigenfunctions of stable diatomic states [J].Mol.Phys.,1997,92:105.
[22]Le Roy R J.Improved parameterization for combined istopomer analysis of diatomic spectra and its application to HF and DF[J].J.Mol.Spectrosc.,1999,194:189.
