大跨度部分斜拉桥最大单悬臂阶段几何非线性影响分析①
2014-07-09孙建渊
万 良, 孙建渊
(同济大学土木工程学院,上海200092)
0 引言
部分斜拉桥要经历一个分阶段施工的过程,结构在施工过程中刚度远比成桥状态小[1],结构的荷载(施工机具、预应力、自重等)是在施工过程中逐级施加的,每个施工阶段都有可能伴随结构形状变化,几何非线性影响可能非常突出,因此对部分斜拉桥施工阶段作非线性分析是十分有必要的.
1 非线性有限元理论

图1 全桥结构模型
当结构受力后随即产生位移,因此,严格讲结构受力的平衡是建立在变形后的几何形状上的.当斜拉桥跨度大,线刚度小,结构的变形大,几何形状的改变则不能忽略.部分斜拉桥的非线性影响因素3个效应,即大变形效应、垂度效应、P-delta效应.
1.1 大变形效应[2]
在荷载作用下,斜拉桥上部结构的几何位置变化显著,从有限元角度来说,结点坐标随荷载的增量变化较大,各单元的长度、倾角等几何特征也相应的产生较大的改变,因此,平衡方程 {F}={K}{δ}不再是线性关系,小变形假设中的叠加原理也不再适用.
1.2 垂度效应[3]
斜拉锁垂度受索力、索长和重力等多重因素控制,导致拉索垂度和索力之间的非线性关系.对于采用一个桁架单元来模拟斜拉索,都采用Enrst修正弹性模量考虑拉索垂度对轴向刚度的影响,Enrst表达式[4]如下:

1.3 P - delta 效应[5]
在斜拉桥中,由于斜拉索的作用,主梁和桥塔要同时承受弯矩和轴力的作用,这样就会产生塔梁单元轴向刚度和弯曲刚度的耦合作用,即P-delta效应,一般采用引入几何刚度矩阵来模拟P-delta效应.
2 计算模型及方法
2.1 工程概况
本文结构分析对象为一混凝土部分斜拉桥,桥梁桥孔布置为13×50+(140+260+140)+12×50m,桥梁全长1790.0m.桥面最大纵坡为2.6%,其中主桥处于R=10000的凸形竖曲线上.主桥采用双塔双索面预应力混凝土部分斜拉桥,主梁采用预应力混凝土单箱三室流线型扁平箱梁.索塔采用双薄壁墩及双柱式索塔,矩形截面,基础采用钻孔群桩基础.取该桥边跨合拢,中跨未合拢的最大单悬臂施工阶段做受力分析,由于全桥具备对称性,所以建立有限元模型只取全桥一半,全桥结构布置如图1所示,MIDAS计算模型如图2所示.

图2 全桥midas计算模型
2.2 桥梁非线性分析方法
斜拉桥的非线性方程组代数解很难直接解出.目前采用数值解的方法主要有增量法、迭代法和混合法求取近似解[6].
3 结果分析
3.1 结构变形分析比较
在最大单悬臂施工阶段,边跨主梁最大位移发生距塔根109米处,中跨主梁最大位移发生在距塔根101米处,分别对该阶段做线性分析考虑垂度效应的部分线性分析、线性二阶分析和完全非线性分析,得到结果如图3所示.
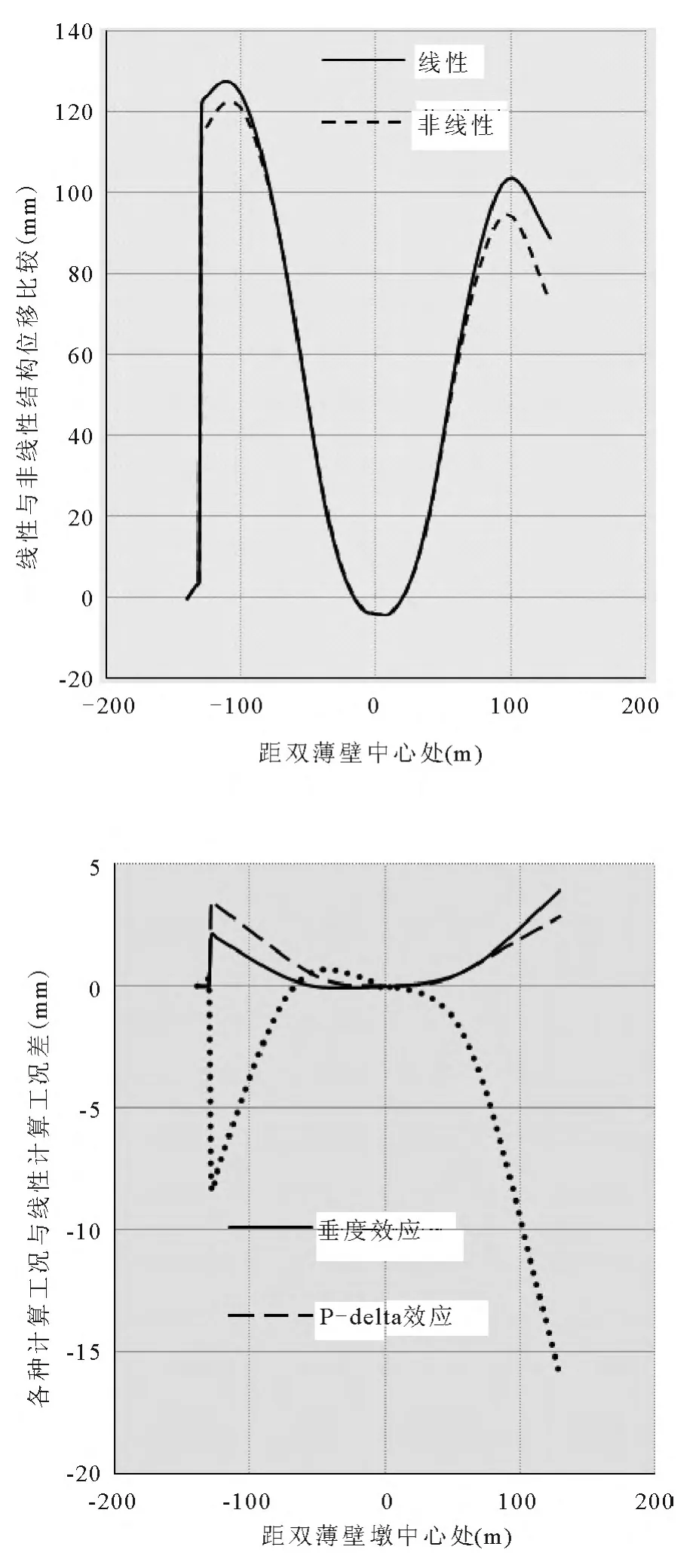
图3 最大单悬臂阶段主梁竖向变形

表1 最大单悬臂阶段主梁竖向变形
从图3及表1可知,在该阶段,各种方法计算几何非线性影响结果相互差值达到了18mm.边跨主梁在悬臂端处的竖向位移,各种计算工况的差值分别2.13mm,3.48mm,-8.35mm,其非线性影响分别为1.74%,2.85%及 -6.84%,边跨最大的竖向位移的完全非线性影响为-3.96%;中跨主梁在悬臂端处的竖向变形,各种计算工况的差值分别3.93mm,2.85mm,-15.92mm,其非线性影响分别为4.43%,3.21%及 -17.94%,中跨最大的竖向位移的完全非线性影响为-9.49%.可以看出,主梁的线性分析与非线性分析结果在近塔根处的非线性影响比较小,随着悬臂长度的增加,各种计算工况的非线性的影响越来越大,几种计算工况带来的非线性影响也比较大.
3.2 主梁内力分析比较
在最大单悬臂施工阶段,最大弯矩出现在距塔根9m处,最大轴力出现在双薄壁墩墩顶主梁处.分别对该阶段做线性分析、考虑垂度效应的部分非线性分析、线性二阶分析及完全非线性分析,得到结果如图4,图5所示.
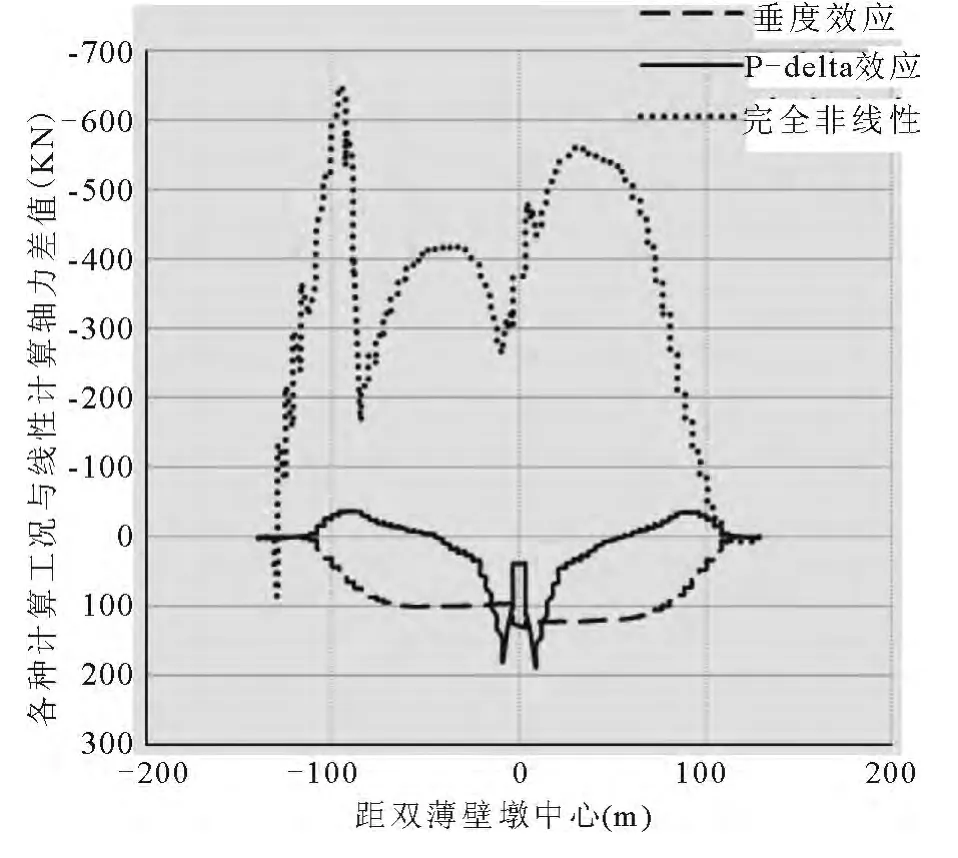
图4 最大单悬臂阶段主梁轴力

图5 最大单悬臂阶段主梁弯矩
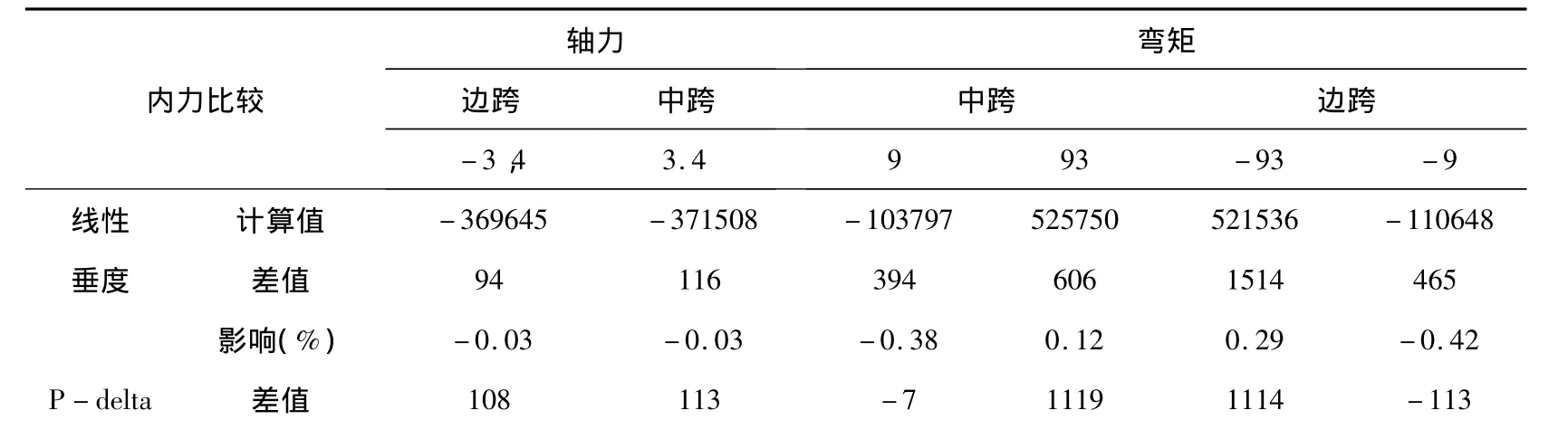
表2 最大单悬臂阶段主梁竖向变形

注:非线性差值=非线性分析计算值-线性分析计算值,非线性影响系数=非线性差值/线性分析差值,轴力采用KN为单位,弯矩采用KN·m为单位,表中-3.4含义为距离主塔中心3.4米处梁单元节点,109,9,93 的含义同理.
从图4、图5及表2可知,在该施工阶段,非线性对结构轴力的影响非常小,最大差值不到700kN,非线性影响在0.2%以内,可以不考虑非线性对轴力的影响.在该施工阶段,垂度效应及P-delta分析对结构弯矩的影响很小,计算值与线性计算十分吻合,而完全非线性对结构弯矩的影响也非常小,最大差值不到16000KN·m,边跨主梁的最大负弯矩发生在薄壁墩墩顶主梁处,非线性差值为-6942KN·m,非线性影响为-1.24%;中跨主梁的最大负弯矩发生在薄壁墩墩顶主梁处,非线性差值为-15743KN·m,非线性影响为-3.03%.在该施工阶段,各种非线性因素影响对结构内力也比较小,可以忽略不计.
4 结论
(1)对于部分斜拉桥来说,施工过程中主梁的非线性效应以及竖向位移随着悬臂长度的增加而增大,在悬臂长度较大时非线性效应的趋势有所加强,在具体施工中应予以注意.
(2)大变形效应在部分斜拉桥几何非线性影响因素中起主导作用,随着悬臂长度的增大,所占的比重逐渐增大.三种非线性效应对弯矩及主梁竖向位移的影响不是趋于同一方向,其中垂度效应及梁柱效应对结构变形均是增大的影响,大变形效应则相反.
(3)通过与线性静力分析对比,可知非线性因素对斜拉桥不同参数的影响大小不尽相同.对于大跨度部分斜拉桥,非线性对主梁和索塔的影响特别突出,在施工控制中应采取相应措施予以调整.
[1] 邓小光.大跨径三塔结合梁斜拉桥施工阶段几何非线性分析[D].武汉:武汉理工大学,2012.
[2] 徐凯燕,魏德敏,刘灿.大跨度斜拉桥几何非线性静力计算分析[J].工程抗震与加固改造,2008(6):64-68.
[3] 彭浩,赵国辉.大跨度斜拉桥非线性静力稳定分析[J].公路交通科技,2011(2):104.
[4] 周念先,杨共树.预应力混凝土斜拉桥[M].北京:人民交通出版社,1989.
[5] 李海波,梅宇.非线性行为对大跨度斜拉桥地震反应影响研究[J].第二十届全国桥梁学术会议论文集(下册),2012:843-848.
[6] 罗堃,宋小斌,甘露.斜拉桥几何非线性静力分析[J].四川建筑,2006.
