一类捕食－食饵系统的多个周期解的存在性①

郑兆岳

(安徽工贸职业技术学院基础部，安徽淮南232007)

0 引言

本文考虑以下时滞捕食－食饵模型

其中 ri(t)，aii(t)，bii(t)，hi(t)，τi(t)，i=1，2，3，θi(t)，i=1，2都是[0，∞)上的正有界连续周期函数．更多的生物学解释见[1～5]．

1 预备知识

引理1．1[6]L是零指标的 Fredholm 映射，N在上是L紧的，若以下条件成立

(i)对任意的λ∈(0，1)，方程Lx= λN(x，λ)的解都满足x∉∂Ω∩Dom L;

(ii)对于任意的x∉∂Ω∩Dom L，QN(x，0)≠0;

(iii)deg{JQN(x，0)，Ω ∩ Ker L，0}≠0

作以下假设

对连续的ω－周期函数f(t)，作记号

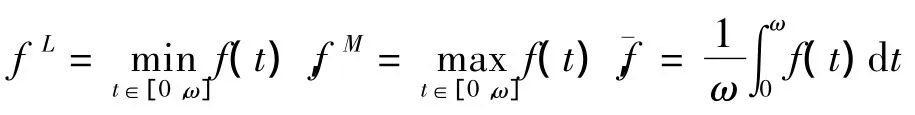
并记

2 系统多个周期解的存在性

定理2．1 若条件(A1)，(A2)，(A3)成立，那么系统(1)至少存在八个周期解．

证明: 令 xi(t)=eui(t)(i=1，2，3)，那么系统(1)可以写成

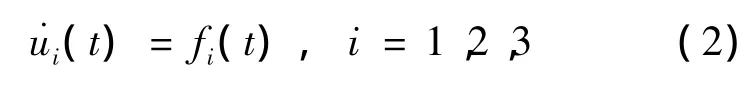
其中

考虑算子方程

Lu=λN(u，λ)，λ∈(0，1)

有

假设存在λ∈(0，1)，u∈X是系统(3)的一个ω周期解，那么存在 ζi，ηi∈ [0，ω]，i=1，2，3，使得．有．则

由(3)及(4)(a)得

由条件(A1)得

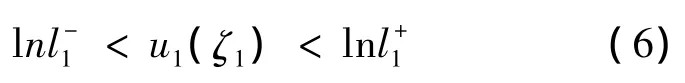
类似，由(5)(a)和条件(A1)得

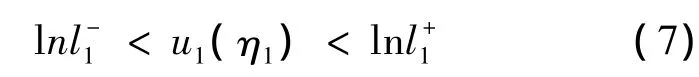
由(5)(b)和条件(A2)得

由(4)(c)和条件(A3)得

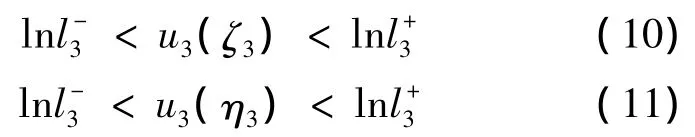
另一方面由(4)(a)和条件(A1)得

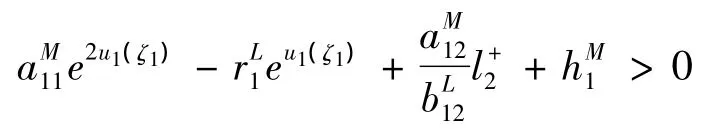
则

同理由(5)(a)和条件(A1)得

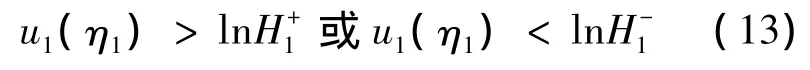
所以lnl+1＞lnH+1，lnl－1＜lnH－1．由[2]中引理2．2得l+1＞H+1，l－1＜H－1由(6)，(7)，(12)，(13)得lnl－1＜u1(η1)＜u1(ζ1)＜lnH－1或lnH+1＜u1(η1)＜ u1(ζ1)＜ lnl+1

则对∀t∈R，有lnl－1＜u1(t)＜lnH－1或lnH+1＜u1(t)＜lnl+1．

同理由(4)(b)、条件(A2)和[2]中引理 2．2，对∀t∈R，有lnl－1＜u2(t)＜lnH－2或lnH+2＜u2(t)＜lnl+2．

由(4)(c)、条件(A3)和[2]中引理2．2，对 ∀t∈R，有lnl－3＜u3(t)＜lnH－3或lnH+3＜u3(t)＜lnl+3．显然lnl±i，lnH±i，i=1，2，3与λ无关．取

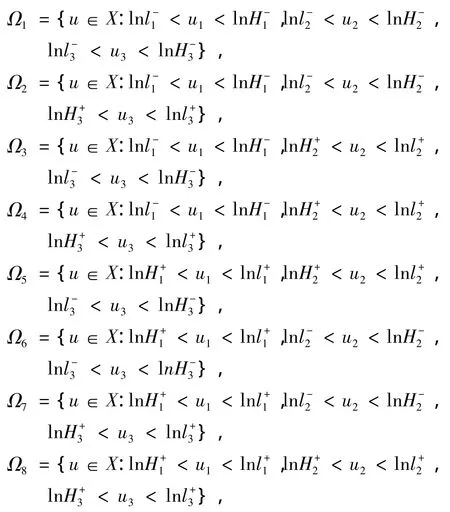
其中 u=(u1，u2，u3)T，Ωi是 X 的有界开集，Ωi∩Ωj，≠ Ø，i≠ j，i，j=1，2，…，8．则 Ωi满足引理1．1条件(1)．

下面验证引理1．1的第二个条件:QN(u，0)≠(0，0，0)T，其中

反证法:假设不成立，存在常向量u=(u1，u2，u3)T∈ ∂Ωi，i=1，2，…，8，使得

由积分中值定理，有 tj∂[0，ω]j=1，2，3使得

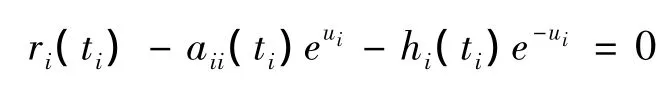
因此

所以 u∈Ωi∩R3，这与u∈∂Ωi∩R3(i=1，2，…，8)矛盾．所以引理1．1的条件(2)得到验证．

最后验证引理1．1的条件(3)．考虑系统

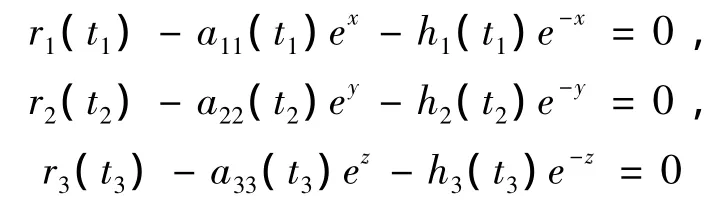
有八个不同的解:

其中

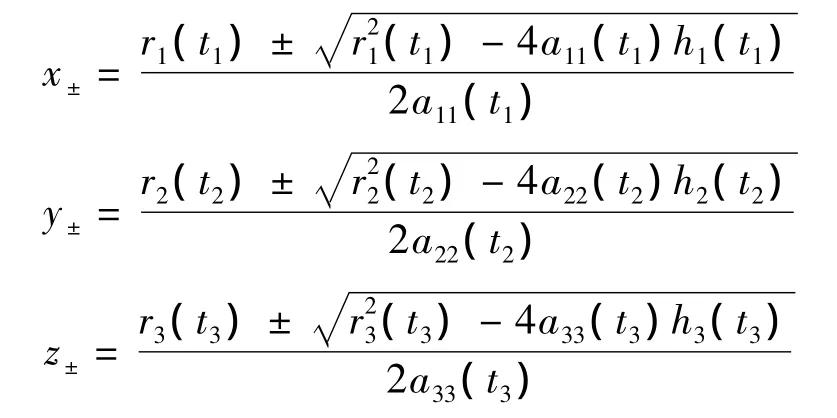
由[2]中引理2．2，易证明

其中

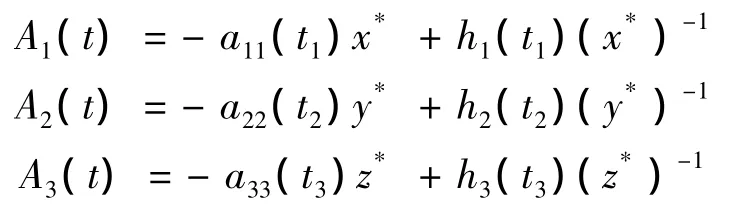
由

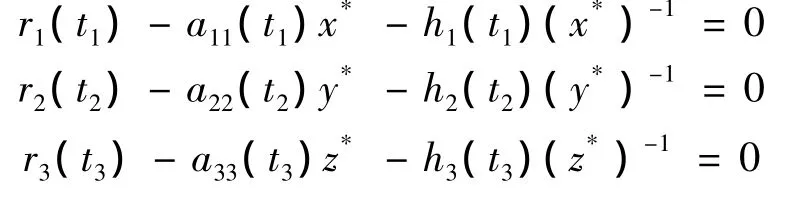
得 deg{JQN(x，0)，Ωi∩ Ker L，0}≠ 0，其中 0=(0，0，0)T．这样就证明了 Ωi满足引理 1．1 的三个条件，所以，系统(1．1)至少有8个ω－正周期解．

[1] Zhien Ma．Mathematical Modelling and Studying on Species E-cology[M]．Anhui Education Press，1996．

[2] Zhao Kaihong，Ye Yuan．Four Positive Periodic Solutions to a Periodic Lotka－Volterra Predatory－Prey System with Harvesting Terms[J]．Nonlinear Anal:RWA，2010，2010，:2448 －2455．

[3] Zhengqiu Zhang，Zhenting Hou．Existence of Four Positive Periodic Solutions for a Ratio－Dependent Predator－Prey System with Multiple Exploited(or Harvesting)Terms[J]．Nonlinear Anal RWA，2010，11:1560 －1571．

[4] Zhouhong Li，Zhao Kaihong，Yongkun Li．Multiple Positive Periodic Solutions for a Non－Autonomous Stage－Structured Predator－ Prey System with Harvesting Terms[J]．Commun Nonlinear Sci Numer Simulat，2010，15:2140 －2148．

[5] Daowei Hu，Zhengqiu Zhang．Four Positive Periodic Solutions to a Lotka－Volterra Cooperative System with Harvesting Terms[J]．Nonlinear Anal:RWA，2010，11:1115 －1121．

[6] Gaines R，Mawhin J．Coincidence Degree and Nonlinear Differential Equations[M]．Berlin:Springer－ Verlag，1977．