集中有序集值信息系统

张腾飞，魏立力

宁夏大学数学计算机学院，宁夏银川 750021

集中有序集值信息系统

张腾飞，魏立力

宁夏大学数学计算机学院，宁夏银川 750021

集值信息系统是完备信息系统的一种推广，按照语义可划分为合取集值信息系统和析取集值信息系统。属性偏好关系也有两种：属性递增偏好有序和属性递减偏好有序。提出一种新的属性偏好关系，建立了一种新的优势关系。这种优势关系能够表示一类属性偏好既不是递增有序也不是递减有序，而是趋近于某个标准值的情形，称这样的优势关系为属性集中有序，它可应用于某些集值信息系统。

集值信息系统；集中有序；属性标准值；优势关系

1 引言

粗糙集理论[1-3]是由波兰学者Paw lak于1982年首先提出的，它是一种刻划不完整性和不确定性的数学工具，能比较有效地分析不完整、不相容、不精确等信息系统，并发现其中隐含的知识，揭示潜在的规律。经典的粗糙集理论以不可分辨关系（等价关系）为基础，其研究对象是完备信息系统，即所处理的信息系统中每个对象的所有属性值都是已知的。当某个信息系统中的某些属性的值未知，即数据是丢失的，或者是只知道部分数据，我们称这样的信息系统为不完备信息系统[4-7]，在许多实际问题中，信息系统往往是不完备的，研究不完备信息系统[8]的策略之一是将不完备信息系统转化为集值信息系统来处理。

Greco等人[9-11]提出了基于优势关系的粗糙集模型，该模型把经典的等价关系推广到具有偏好的优势关系，为解决具有偏好信息的多属性决策问题提供了思路。Qian等人[12-13]提出了集值有序信息系统模型，用来处理属性偏好有序且属性取值为集值的情况。对于集值信息系统语义上的理解有多种，Guan和Wang[14]将其归结为两类：

第一类：合取集值信息系统。在这类系统中，对象在属性集值中的取值是合取的，即对象可以取到属性值中的所有值。例如，属性a表示属性“会讲一种语言”，对象x在属性a下的取值f(x)={英语,法语,德语}可以理解为对象x会讲英语、法语和德语三种语言。

第二类：析取集值信息系统。在这类系统中，对象在属性集值中的取值是析取的，即只能取到属性集值中的某一个值。例如，属性a表示属性“会讲一种语言”，对象x在属性a下的取值f(x)={英语,法语,德语}可以理解为对象x会讲英语、法语和德语三种语言中的某一种语言。

对于具有未知属性值的不完备信息系统可看作是析取集值信息系统，也可看作合取集值信息系统，这要视情况具体分析。在实际应用中，集值信息系统中属性往往含有偏好信息，从而导致对象之间往往存在优劣关系，因此，研究具有二元偏好关系的集值信息系统是具有重要意义的。

目前，针对偏好信息的处理主要从两个方面来定义了优势关系：一是数值越大越好（递增偏好有序）；二是数值越小越好（递减偏好有序）。然而，这两种定义方法并不能处理一些实际问题。例如，对病人进行健康诊断时，对于体温这一指标，不是越高越好，也不是越低越好，而是越接近人的正常体温越好。因此，有必要提出一种新的优势关系定义方法。本文针对这种情况，提出了一种特殊的属性偏好关系，建立了一种新的优势关系，这种优势关系能够解决一类属性偏好既不是递增有序也不是递减有序，而是属性值趋向于标准属性值的问题，称之为属性集中有序。

2 预备知识

本部分引入的定义出自文献[12-13，15]，现罗列如下。

定义1（集值信息系统）称S=(U，A，V，f)是集值信息系统，其中，U={x1，x2，…，xn}为非空有限对象集合，也称为论域，A={a1，a2，…，am}为非空有限的属性集合，V=∪a∈AVa是属性值的集合，Va表示属性a∈A的值域，f:U×A→2V是一个集值映射，满足| |f(x，a)≥1（对于∀x∈U，a∈A)，其中|·|表示集合中元素的个数。

对于集值信息系统语义上的理解有多种，Guan和Wang将其归结为合取集值信息系统和析取集值信息系统两类，在引言中已经讨论过，这里不再赘述。

定义2（有序信息系统）给定信息系统S=(U,A,V,f)，若信息系统S中所有的条件属性都是递增或递减偏好有序，则称信息系统S为有序信息系统。

表示在属性a∈A下，y至少和x一样好。下面将在数值域中考虑偏好属性的序关系，即Va⊆N（其中N表示数值），则⇔f(y，a)≥f(x，a)（条件偏好属性a递增有序）或⇔f(y，a)≤f(x，a)（条件偏好属性a递减有序）。

定义3（优势关系和优势类）给定有序信息系统S=(U，A，V，f)，属性子集B(B⊆A)，优势关系定义为：

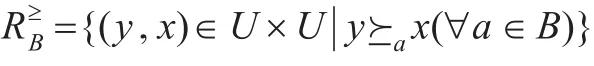
若属性子集B=B1∪B2，其中，属性子集B1中的偏好关系递增有序，属性子集B2中的偏好属性递减有序，则优势类的定义为：

定义4（析取集值有序信息系统）给定集值信息系统S=(U，A，V，f)，对于任意的x∈U和任意的a∈A，若对象x在属性值f(x，a)中的取值都是析取的，即只能取到属性集值中的某一个值，则称S为析取集值信息系统。若在析取集值信息系统S中进行决策规则获取时，总要考虑对象间的优势关系，则称S为析取集值有序信息系统。

显然，析取集值有序信息系统是同时满足析取集值信息系统和有序信息系统定义的一种特殊的信息系统。

定义5（合取集值有序信息系统）给定集值信息系统S=(U，A，V，f)，对于任意的x∈U和任意的a∈A，若对象x在属性值f(x，a)中的取值都是合取的，即要取到属性集值中的每一个值，则称S为合取集值信息系统。若在合取集值信息系统S中进行决策规则获取时，我们也总要考虑对象间的优势关系，则称S为合取集值有序信息系统。

显然，合取集值有序信息系统是同时满足合取集值信息系统和有序信息系统定义的一种特殊的信息系统。

3 集中有序的集值信息系统

对象在属性下的最优值叫做属性标准值，某一属性a的属性标准值用Ma表示，高于或低于属性标准值的值都不是最优的。例如，若属性a表示“人的体温指标”，那么Ma就表示人体温的标准值，也即是人的正常体温，高于或低于正常体温的温度都不是最优的。

在集值信息系统S=(U，A，V，f)中，Va表示属性a∈A的值域，易知属性a的标准值Ma∈Va。非空有限的属性集合A={a1，a2，…，am}，其中a1，a2，…，am的属性标准值分别为Ma1，Ma2，…，Mam，可以用MA={Ma1，Ma2，…，Mam}，表示属性标准值集。

3.1 集中有序的完备信息系统

定义6（完备信息系统的属性集中有序）在完备信息系统S=(U，A，V，f)中，Va表示属性a的值域，Ma表示属性a的标准值，Ma∈Va。对于对象x，y∈U，在属性a下的取值分别为f(x，a)∈Va、f(y，a)∈Va，若满足

则称在属性a∈A下，y至少和x一样好，称属性a集中有序。

这里的集中有序就是属性值无论从左侧还是右侧，越靠近属性标准值的对象就越有优势。属性集中有序是区别于属性递增有序和属性递减有序的一种特殊的有序关系。满足集中有序的条件属性，也称之为具有偏好关系的属性。

用表示在属性a∈A下，y优于x，也即y至少和x一样好。那么定义6可用下式描述。

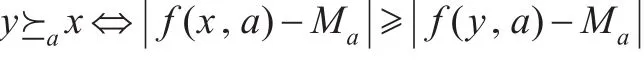
定义7给定集中有序完备信息系统S=(U，A，V，f)，属性子集B(B⊆A)，优势关系定义为：

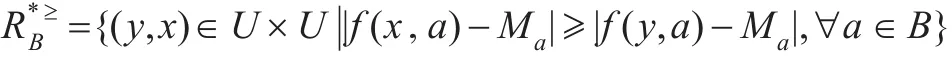
对象x的优势类相应地为：

例1表1所示的为一个完备信息系统，其中对象集U={x1，x2，…，x10}，属性集A={a1，a2，a3，a4}，属性集A中的偏好属性集中有序，属性值域Va1=Va2=Va3=Va4= {1，2，3，4，5}，属性标准值Ma1=Ma2=Ma3=Ma4=3。

表1 一个完备信息系统

则信息系统在优势关系下的优势类分别为：

定理1给定集中有序完备信息系统S=(U，A，V，f)，属性子集B(B⊆A)，则

（1）满足自反性、传递性；

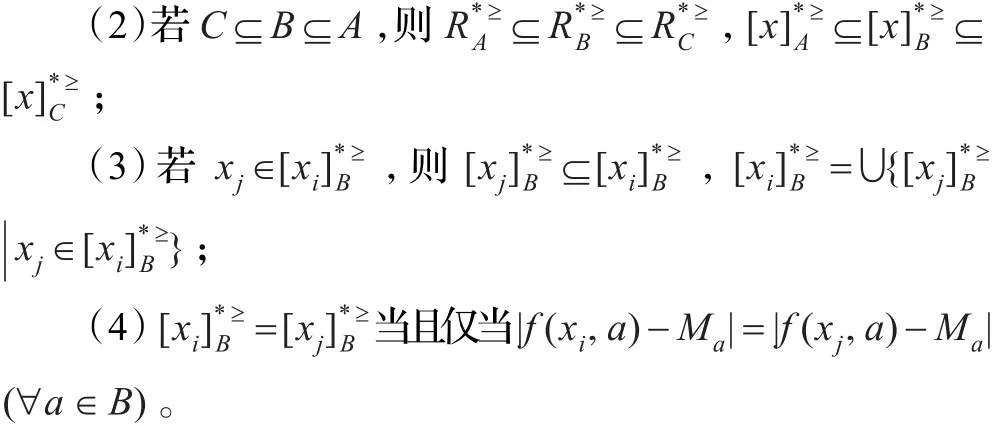
证明（1）和（2）可以由优势关系和优势类的定义直接得到。

3.2 集中有序的析取集值信息系统

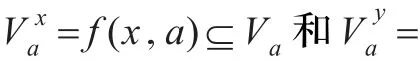
则称在属性a∈A下，y至少和x一样好，称属性a集中有序。

用表示在属性a∈A下，y优于x，也即y至少和x一样好。那么定义8可用下式描述。

注：Va表示属性a∈A的值域，把Va中每个值与属性标准值Ma相减后取绝对值，把所得值的集合表示为Wa。对于两个对象x，y∈U，在属性a∈A之下，他们有各自的属性值域和，同时也有各自的和，那么，定义8也可用下式表示。

例2表2所示的为一个析取集值信息系统，其中对象集U={x1，x2，…，x10}，属性集A={a1，a2，a3，a4}，属性集A中的偏好属性集中有序，属性值域Va1=Va2=Va3=Va4= {1，2，3，4，5，6，7}，属性标准值Ma1=Ma2=Ma3=Ma4=4。

表2 一个析取集值信息系统

则信息系统在优势关系下的优势类分别为：

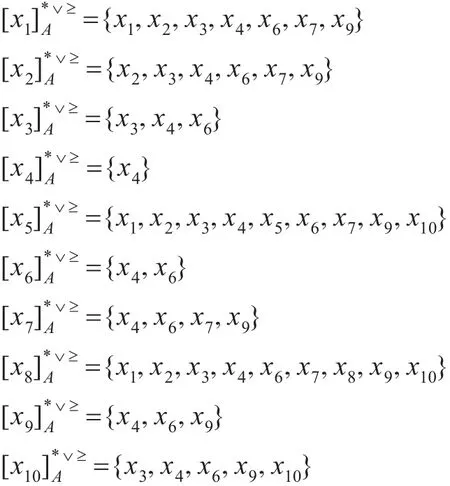
定理2给定析取集中有序集值信息系统S=(U,A,V,f)，属性子集B(B⊆A)，则

证明（1）和（2）可以由优势关系和优势类的定义直接得到。

3.3 集中有序的合取集值信息系统

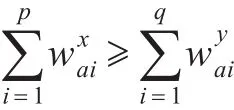
则称在属性a∈A下，y至少和x一样好，称属性a集中有序。

用表示在属性a∈A下，y优于x，也即y至少和x一样好。那么定义10可用下式描述。

定义11（优势关系和优势类给定合取集值有序信息系统S=(U，A，V，f)，属性子集B(B⊆A)，优势关系定义为：

对象x的优势类相应地为：

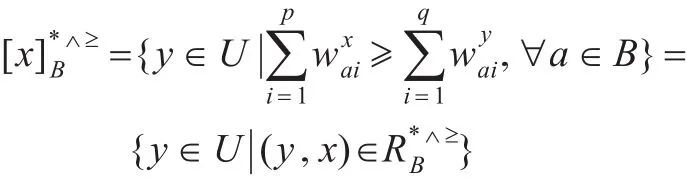
例3表3所示为一个合取集值信息系统，其中对象集U={x1，x2，…，x10}，属性集A={a1，a2，a3，a4}，属性集A中的偏好属性集中有序，属性值域Va1=Va2=Va3=Va4= {1,2,3,4,5,6,7}，属性标准值Ma1=Ma2=Ma3=Ma4=4。

表3 一个合取集值信息系统

则各对象在优势关系下的优势类分别为：

定理3给定合取集中有序集值信息系统S=(U,A,V,f)，属性子集B(B⊆A)，则

（1）满足自反性、传递性；

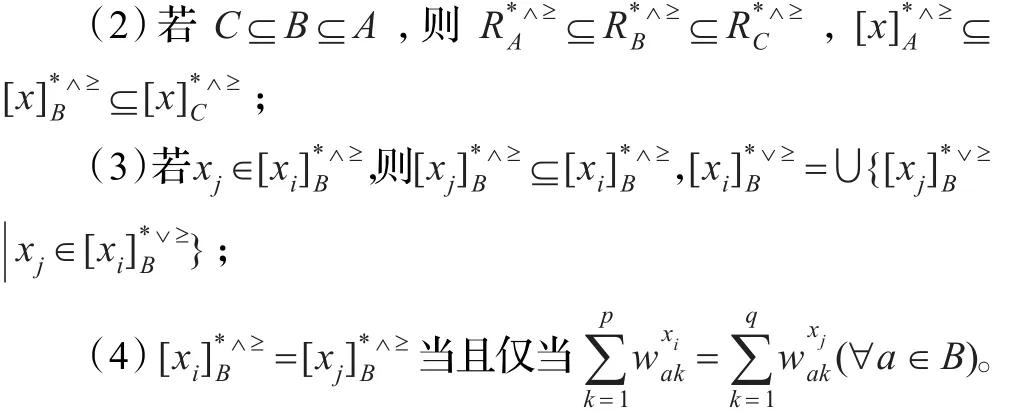
证明（1）和（2）可以由优势关系和优势类的定义直接得到。

4 结束语

目前，针对偏好信息的处理主要从两个方面来定义了优势关系：一是数值越大越好（递增偏好有序）；二是数值越小越好（递减偏好有序）。然而，这两种定义方法并不能表示某些情形。本文提出一种新的条件属性偏好关系，建立了一种新的优势关系，这种优势关系能够表示一类条件属性偏好既不是递增有序也不是递减有序，而是趋近于某个标准值的情形。然后，把这种优势关系分别应用于析取集值信息系统和合取集值信息系统，基于这种优势关系，还可以进一步研究对象排序、属性约简和决策分析等问题。

[1]Paw lak Z.Rough sets[J].International Journal of Computer and Information Science，1982，11（5）：341-356.

[2]Paw lak Z.Rough sets theory and its applications to data analysis[J].Cybernetics and System，1998，29（2）：661-688.

[3]Paw lak Z.Rough sets and intelligent data analysis[J].Information Science，2002，147（1）：1-12.

[4]K rysckiew icz M.Rough set to incomplete information system[J].Information Sciences，1998，112（1）：39-49.

[5]Stefanow ski J，Tsoukias A.Incomplete information tables and rough classification[J].Computational Intelligence，2001，17（10）：545-566.

[6]Grzymala-busse J W.Charateristic relations for incomplete data：a generalization of the indiscernibility relation[C]//Transactions on Rough Sets VI，LNCS 3066. Berlin：Springer，2004：244-253.

[7]王国胤.Rough集理论在不完备信息系统中的扩充[J].计算机研究与发展，2002，39（10）：1238-1243.

[8]王国胤.Rough集理论与知识获取[M].西安：西安交通大学出版社，2001.

[9]Greco S，Matarazzo B，Slow inski R.A new rough set approachto multicriteria and multiattribute classification[C]//Lecture Notes in Artificial Intelligence，1998，1424（1）：60-67.

[10]Greco S，Matarazzo B，Slow inski R.Rough sets theory for multicriteria decision analysis[J].European Journal of Operational Research，2001，129（1）：1-47.

[11]Greco S，Matarazzo B，Slow inski R.Rough sets methodology for sorting problem s in presence of multiple attributes and criteria[J].European Journal of Operational Research，2002，138（2）：247-259.

[12]Qian Y H，Dang C D，Liang J Y，et al.Set-valued ordered information systems[J].Information Sciences，2009，179（16）：2809-2832.

[13]Qian Y H，Dang C D，Liang J Y，et al.On dominance relations in disjunctive set-valued ordered information systems[J].International Journal of Information Technology and Decision Making，2010，9（1）：9-33.

[14]Guan Y Y，Wang H K.Set-valued information systems[J]. Information Sciences，2006，176（17）：2507-2525.

[15]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003.

ZHANG Tengfei,WEI Lili

College of Mathematics and Computer Science,Ningxia University,Yinchuan,Ningxia 750021,China

Set-valued information system is a promotion of complete information system.According to semantics,it can be divided into conjunctive set-valued information system and disjunctive set-valued information system.There are also two kinds of attribute preference relations：attribute increasing preference order and attribute decreasing preference order. This paper focuses on a new attribute preference relation and establishes a new dominance relation.This new dominance relation can represent a kind of attribute preference which is not the increasing preference order and not the decreasing preference order,but the condition attribute values tend to the standard values of attribute,such a dominance relation is called as attribute ordered concentration,it can be applied to some set-valued information system s.

set-valued information systems;ordered concentration;standard values of attribute;dominance relation

A

TP18

10.3778/j.issn.1002-8331.1209-0320

ZHANG Tengfei,WEI Lili.Set-valued in formation system s based on ordered concentration.Computer Engineering and Applications,2014,50（16）：140-145.

国家自然科学基金（No.11261044）；宁夏高等学校科学技术研究项目。

张腾飞（1988—），男，硕士研究生，研究领域为应用统计与数据分析；魏立力（1965—），通讯作者，男，教授，研究方向为应用统计与数据分析、人工智能的数学基础。E-mail：weill866@163.com

2012-09-27

2012-11-23

1002-8331（2014）16-0140-06

CNKI网络优先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1528.024.htm l