自反馈生物激励神经网络机器人路径规划

吕战永，曹江涛

LV Zhanyong,CAO Jiangtao

辽宁石油化工大学 信息与控制工程学院，辽宁 抚顺 113001

School of Information and Control Engineering,Liaoning Shihua University,Fushun,Liaoning 113001,China

1 引言

路径规划是移动机器人自主导航的关键技术之一。移动机器人路径规划是指在有障碍物的工作环境中，寻找一条从给定起点到终点的适当运动路径，使机器人在运动过程中能安全、无碰地绕过所有障碍物。移动机器人的路径规划方法可分为基于地图的全局路径规划和基于传感器的局部路径规划[1]。

人工势场法，遗传算法，人工神经网络等是现在运用在机器人全局路径规划中比较成功的算法。传统的人工势场法存在几大缺陷：在相近的障碍物之间存在盲区不能发现路径；当目标点附近处有障碍物时机器人无法到达目标点[2]。遗传算法在环境中存在大量复杂的不规则障碍物时运算速度很慢。一些传统神经网络模型需要学习并且仅能处理在静态环境下的情况[3]。SimonX.Yang提出了生物激励神经网（Biologically Inspired Neural Network，BINN）路径规划方法来解决动态环境中生成实时的避障路径，它不需要学习过程，并且在网络结构中各神经元之间只存在局部的侧连接，计算速度较快因此能对动态环境中的变化作出迅速反应[4-5]。但是这种方法也存在静态路径规划中所得路径不是最优或者次优路径，在一些复杂动态环境中对动态目标追踪效果不理想的情况。文中针对这些情况，提出了带自反馈的BINN，并引入了新的权值函数求取方法。与原方法比在多个指标上得到了改善。

2 BINN路径规划原理

1999年SimonX.Yang把BINN应用在机器人路径规划上，它的应用原理是将移动机器人的运动空间映射为由BINN组成的拓扑状态空间，其中每一个神经元活性值变化由方程（1）来求取。

式中，xi为第i个神经元的激活值，A为正常数，代表衰减率，B为神经元活性值的上界，-D为神经元活性值的下界，Ii为第i个神经元的外部输入，k为第i个神经个神经元的激励输入，S-=(D+xi)[xi]-表示抑制输入。ωij为第 j个神经元到第i个神经元的连接权，计算公式如式（2）所示：

式中，|qi-qj|为相邻神经元qi和qj之间的欧氏距离，μ和r为正的常数，显然ωij=ωji，即ωij和ωji是对称的，非线性门限值函数为：

通过上述一组方程，经过一定次数的迭代计算就能得到BINN拓扑空间的神经元活性值状态图，沿着活性值的最大梯度上升方向就能找到一条由起点到目标点的路径[4-6]。

3 基于自反馈BINN的建模及路径规划

3.1 提出自反馈BINN的原因

BINN虽然有许多优点但是也存在不足。

图1是BINN在静态环境下的路径规划仿真，发现在路径规划的过程中BINN路径规划方法在多个地方出现了波浪形路径，造成了路径的加长从而使得路径不是最优或者次优。

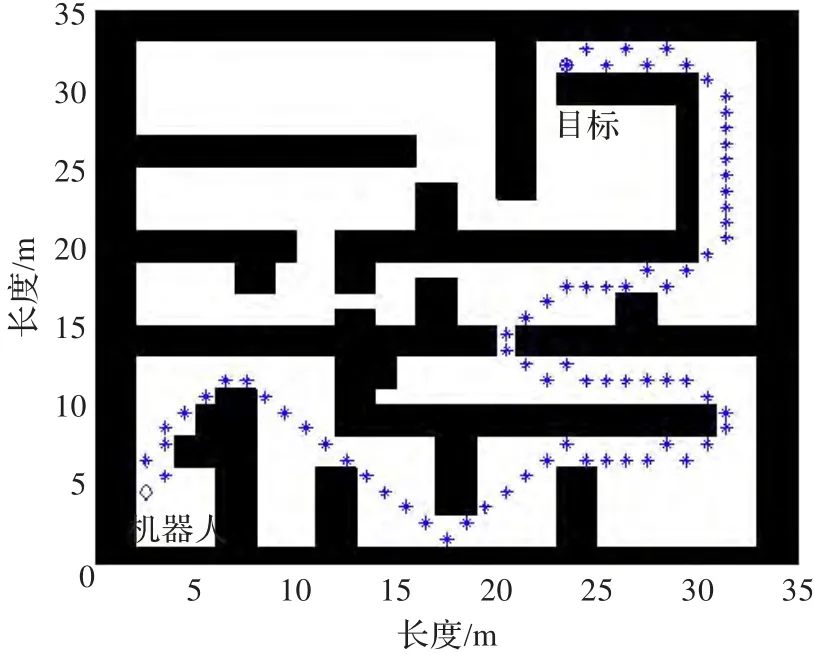
图1 BINN在静态环境中的路径生成

图2 （a）是BINN方法在追踪动态目标时的路径生成，机器人和目标的运动速度相同，由于机器人对运动目标的追踪不够灵敏，因此当运动目标到达终点时机器人都无法对运动目标进行无差别跟踪。

3.2 自反馈BINN

针对上面的问题，提出了自反馈BINN，它有两项改进：

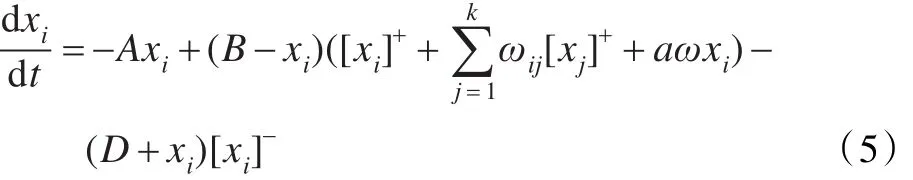
图2 两种算法对运动目标的追踪

第一：在神经元上增加一个自反馈链接设计了自反馈权值函数求取方法，增强其前一刻的活性值状态对下一刻的影响，从而起到抑制波浪形路径产生的作用。自反馈BINN活性值方程如下：在式（5）中a为一个常数，ω为自反馈权值函数，由式（6）可知当神经元当前时刻激活值和前一刻激活值之差的绝对值增大时，自反馈权值ω就会变小，使最终的激活值不会出现激烈的变化，从而避免了图1中所出现的因激活值突变而形成的波浪形的不平滑路径。

第二：权值大小与神经元距离之间的关系并不是简单的线性关系，而是一种复杂的非线性关系，因此采用了文献[7]中所用的指数型的求取方法，从而增强算法对运动目标的追踪能力，其权值求取方式如式（7）：

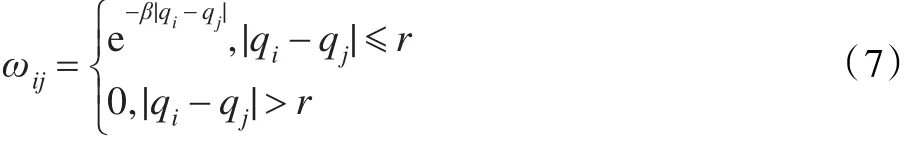
式中，β为正常数，其他参数与BINN相同。

在增加自反馈和新的权值求取方式后算法能够对运动的目标进行无差别的跟踪如图2（b）所示，机器人经过简单的变向之后就可以无差别地跟踪运动的目标。

3.3 基于自反馈BINN模型的环境建模

进行机器人路径规划首先要对机器人的运动环境进行建模。先用栅格法把机器人的运动空间分割，然后把机器人的运动空间映射为由自反馈BINN组成的拓扑状态空间，每一个栅格都对应一个神经元，机器人所要达到的目标位置对应的神经元初始激活值为1，障碍物所对应的神经元初始激活值为 -1，机器人及自由空间所对应的神经元初始激活值都为0，其中拓扑状态空间的每一个神经元的激活值变化都由方程（5）来决定。当自反馈BINN应用于机器人路径规划时，第i个神经元的外部输入Ii的求取方式如下：

式中的E是一个远远大于神经元活性值上界B的正的常数，一般情况下取值100。

3.4 自反馈BINN路径规划

第一，先用栅格法把机器人的运动空间建模，然后把机器人的位姿空间映射到神经网络中，每一个栅格都对应一个神经元。

第二，神经网络中除目标和障碍外的所有神经元激活值初始化为零，并利用式（6）通过迭代计算使目标点的神经元激活值经由神经元之间的侧连接传播到出发点。

第三，当目标激活值传播到起始点时，利用爬山法搜索当前位置邻域内激活值最大的神经元，如果邻域内神经元激活值都不大于当前神经元的激活值，则机器人保持在原处不动；否则机器人的下一个位置为其邻域内具有最大激活值的神经元[7]。

第四，如果机器人的位置坐标和目标的位置坐标重合，则路径规划过程结束，否则转第三步。

4 自反馈BINN机器人路径规划仿真

为了验证本文提出的自反馈BINN移动机器人路径规划方法的有效性和可行性，利用Matlab2010a对本文提出的路径规划算法进行了计算机仿真实验。机器人运动环境空间为二维，机器人也为二维，机器人模型为圆形，机器人是完整的，可以在原地转向。地图大小为35 m×35 m，由1 225个35×35的神经元方阵组成的网络结构来表示，星型符号（*）所组成的轨迹曲线表示机器人的规划路径，机器人由一个（*）位置到达临近（*）位置为一次运动，机器人每一次横向和纵向运动都为1 m，每一次斜向运动为1.414 m。圆圈（o）所组成的轨迹曲线为目标的运动轨迹，黑色方格表示的是障碍物，符号（+）所组成的轨迹曲线表示的是移动障碍运动的轨迹，菱形图标表示机器人所在的初始位置。自反馈BINN模型的参数设置为 A=1，B=D=1，E=100，a=0.7，r=1.5，β=6 。

4.1 静态环境下的仿真与比较

这一部分将在静态地图环境下对自反馈BINN算法与BINN算法[4]进行仿真比较。

仿真1是U型地图环境下的仿真，U型地图是测试机器人路径规划能力的经典地图，在此次仿真中目标起始的坐标位置为（17，32），机器人的起始坐标位置为（17，23），机器人的移动速度为1 m/s，仿真结果如图3所示。

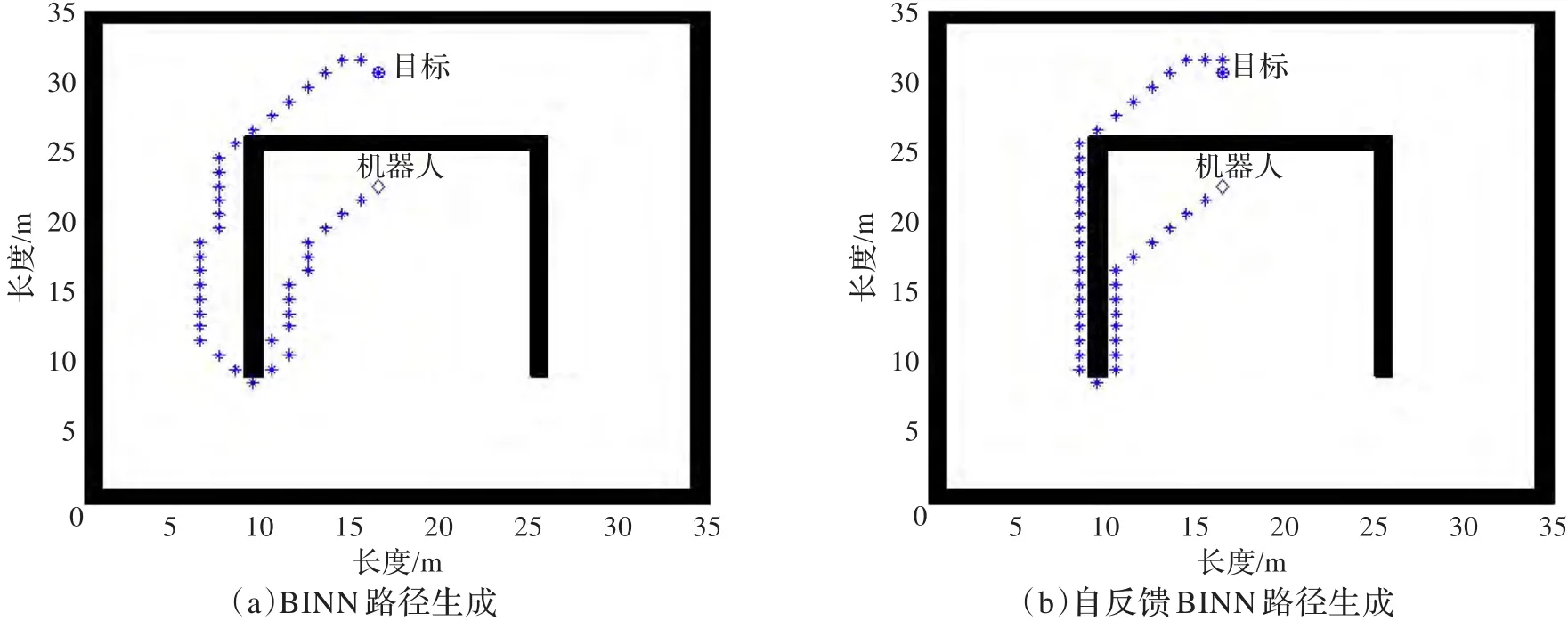
图3 U型地图仿真

在图3（a）中可以看到路径总共有15次变向，在无障碍时的波浪形运动一次，最后它的路径长度为47.694 m。在图3（b）中路径总共有8次变向，在无障碍处没有波浪运动，最后它的路径总长度为44.796 m。因此可以看出自反馈BINN比单纯的BINN能生成更短更加平滑的无碰撞路径。在现实生活中变向会浪费更多的时间和能源，自反馈BINN比BINN少了7次转向，因此自反馈BINN比单纯的BINN更加节能环保。两者具体的数据比较如表1。

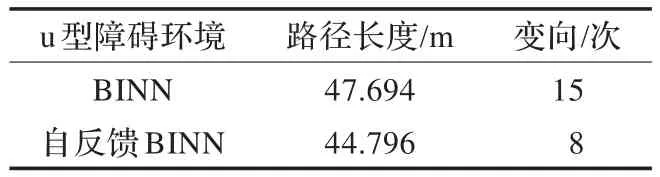
表1 仿真1比较结果

4.2 复杂动态环境下仿真

这一部分将在复杂动态地图环境下进行路径规划仿真，地图中目标是运动的，不但有固定的障碍，同时还有运动着的障碍，仿真中机器人每一次横向和纵向运动都为1 m，每一次斜向运动为1.414 m。

仿真2是在动态的地图环境中追踪移动的目标，并同时对移动的障碍作出反应。目标以1 m/s的速度由左至右从（1，34）运动到终点坐标（34，33），先阶梯向下运动，然后阶梯向上运动，最后停留在坐标（34，33），在这期间目标共变向11次。移动障碍以1 m/s的速度由左至右从（4，21）移动到（29，21）。机器人的起始位置为（23，10），仿真结果如图4所示。在图4（a）中是BINN算法所生成的实时避障路径，当目标开始移动时机器人也开始向相同的方向移动，当机器人快要通过右侧固定障碍时，从左侧移动过来的移动障碍正好把右侧出口堵住，机器人重新从左侧通过了障碍，在这个过程中机器人有两次在无障碍处出现波浪形的运动，在随后的过程中机器人无法对机器人进行无差别的追踪，在整个路径中机器人一共转向23次，最终路径长度为67.36 m。图4（b）是自反馈BINN生成的实时避障路径，其避障路径生成的过程同BINN方法的相似。但是当机器人通过障碍物后可以对移动的目标进行无差别追踪。在这个过程中机器人转向13次，最终路径长度为66.178 m。因此可以看出在复杂的动态环境中自反馈BINN比单纯的BINN能生成更短更加平滑的实时无碰撞路径，并且能对运动目标进行无差别追踪。在现实生活中变向会浪费更多的时间和能源，自反馈BINN比BINN少了10次转向，因此自反馈BINN比单纯的BINN更加节能环保。两者具体数据比较如表2。

4.3 仿真结果讨论

通过对新算法在动态和静态地图下的模拟仿真，可以总结出自反馈BINN算法模型的优点：

图4 复杂动态环境仿真

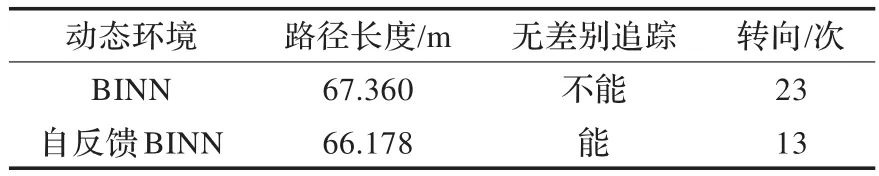
表2 仿真2比较结果

（1）自反馈BINN算法能够使机器人通过可行路径到达目标并同时消除了波浪形路径的产生，并且能够大量减少转向次数。

（2）动态环境下，改善了BINN追踪效果不理想的情况，能够预判目标运动的方向从而在和目标同速的情况下对运动的目标进行无差别追踪。

5 结论

文章提出了一种基于BINN的带自反馈的BINN移动机器人路径规划方法，在静态和动态的环境下和文献[4]的方法进行了仿真比较。结果表明该路径规划方法比原方法有了很好的提高，不仅保证了移动机器人在静态环境下能够得到更优的路径，而且在动态环境中给机器人提供了更强的对目标的追踪能力。

[1]席裕庚，张纯刚.一类动态不确定环境下机器人的滚动路径规划[J].自动化学报，2002，28（2）：161-175.

[2]罗乾又，张华，王姮，等.改进人工势场法在机器人路径规划中的应用[J].计算机工程与设计，2011（4）.

[3]魏冠伟，付梦印.基于神经网络的机器人路径规划算法[J].计算机仿真，2010，27（7）：112-116.

[4]Yang S X，Luo C.A bioinspired neural network for realtime concurrent map building and complete coverage robot navigation in unknown environments[J].IEEE Transactions on Neural Networks，2008，19（7）：1279-1298.

[5]Yang S X，Meng M.An efficient neural network approach to dynamic robot motion planning[J].Neural Networks，2000，13（2）：143-148.

[6]范莉丽，王奇志.改进的生物激励神经网络的机器人路径规划[J].计算机技术与发展，2006，16（4）：19-21.

[7]宋勇，李贻斌，栗春，等.基于神经网络的移动机器人路径规划方法研究[J].系统工程与电子技术，2008，30（2）：316-319.