FAHP改进Shapley值法进行工程科技创新收益分配

盛松涛 ，张飞涟 ，张贵金

SHENG Songtao1，2,ZHANG Feilian1,ZHANG Guijin2

1.中南大学 土建学院，长沙 410083

2.长沙理工大学 水利工程学院，长沙 410004

1.Civil Engineering and Architecture Institute,Central South University,Changsha 410083,China

2.Hydraulic Engineering Institute,Changsha University of Science and Technology,Changsha 410004,China

1 引言

随着科学技术和社会的不断发展，现代工程项目中新技术出现和更迭的速度越来越快，各个创新主体都会面临技术资源短缺的问题，而合作创新恰是解决这一问题的重要途径[1]。工程合作创新是指工程企业之间或企业、研究机构和高等院校之间的联合创新行为[2]。

创新联盟成员发挥各自所长，通过创新合作实现“双赢”或“多赢”的目标，在强调集体收益的基础上，实现每个成员的收益[3]。然而，如果收益分配不合理，成员企业可能就会产生消极合作，互相推诿甚至猜疑，使创新失去动力，影响创新合作绩效。反之，如果收益分配方法使各成员感觉比较公平满意，则有助于激励联盟成员的创新积极性，使合作顺利进行，提高创新绩效。目前，在实际工程项目中的创新收益分配一般由业主主导，创新成果与收益主要归业主所有，根据业主的判断分配部分经济收益给其他成员；而一旦创新成果达不到预期工程目标，业主的损失又是最大的。这种以业主为主导的分配方法由于本位主义与主观判断的局限性，很难科学地体现“多贡献高收益，高风险高收益”的公平原则。因此，必须围绕工程技术合作创新的收益分配来设计一套合理的分配机制。

对于创新合作成员间的收益分配，国内外学者已经提出了一些解决方法，主要有Nash合作解法、Shapley法和综合协商法等。Kuzmin和Emelichev研究了不确定性条件下企业间的有限合作博弈情况，利用企业间具有相关性的线性支付函数研究Nash均衡进行分配的最优性与稳定性[4]。Immorlica，Kleinberg等运用合作博弈理论研究了联盟最大化收益及其分配问题[5]。Guardiola针对供应链联盟的供应商管理库存集成策略，应用合作博弈理论，提出将解决多人合作博弈问题的Shapley值法用于解决联盟利益分配问题[6]。张捍东和生延超等结合风险补偿机制和网络分析法（ANP）改进传统的Shapley值法去探究不同联盟的利益分配策略[7-8]。杨晶提出了利益综合协商法的思想，为不同的利益分配方案确定权重，折中得到一种综合的利益分配方法，来解决多种协商方案都不一致的问题[9]。从实际应用情况来看，Shapley值法避免了平均分配、吃大锅饭的现象，调动了合作成员企业的积极性。相对于其他两种方法容易掌握，可操作性好，应用更为广泛。但是，该方法未能充分体现联盟成员在合作中的重要程度与承担的风险大小，因此，用夏普利值法进行收益分配也有它的不足之处[10]。

2 技术创新联盟收益分配的Shapley值法

2.1 Shapley值法基本理论

Shapley值是由 Shapley L.S（1953）提出用来解决多成员合作博弈问题的一种数学方法，实质上也是考虑联盟成员博弈时内部的一种利益分配方案。当多个成员从事某项经济活动时，对于他们之中若干人组合的每一种合作形式，都会得到一定的收益，当人们之间的利益活动非对抗性时，合作中成员数的增加不会引起效益的减少，这样全体成员的合作将带来最大效益，Shapley值法是分配这个最大效益的一种方案，它实现了联盟总体利益在各成员之间的较公平和有效分配[11]。研究表明，基于Shapley值的科技创新联盟合作收益分配方法具有稳定性（其解必定惟一且可行），同时完全可以满足可转移支付合作博弈解的条件。Shapley值体现的是每个联盟成员对该联盟的平均贡献，反映了个人在集体中的重要性。基于Shapley值的科技创新联盟合作收益分配方法的最大优点在于其分配原理和分配结果能够被所有合作方视为公平，分配结果易于被合作各方接受，因此可以将这种方法应用于工程科技创新联盟合作收益分配问题中。

定义：对给定的n个科技创新成员联盟合作博弈，设F是定义在 N=(1，2，…，n)上的特征函数，由F决定的一个分配向量由 φ(F)=(φ1(F)，φ2(F)，…，φn(F))，若同时满足以下公理[11]：

（1）对称性

设π是 N=(1，2，…，n)的一个排列，即 N到它自身的一一对应，如π是i的对应，πs是 s的对应(s∈N)。若 记 (πF)=F(πs)，∀s∈N ，则 对 于 i=1，2，…，n 有φπ1(πF)= φ1(F)。

该公理表示，每个联盟成员的分配与其被赋予的记号无关，即局中人具有平等关系。

（2）有效性

如果对于所有包含i的子集s都有F(s/i)=Fφ(s)，则

该公理表示，若成员i对于每一个其参加的合作都没有贡献，那么就不应该从全体合作的效益中获得报酬，另外，各成员分配之和应等于全体合作的效益。

（3）可加性

对于定义在i上的任意两个特征函数u和v：

Φ(u+v)=Φ(u)+Φ(v)

这个公理说明，每个参与联盟的成员在和博弈中，分配的份额是在两个分博弈中分配的份额之和。

在以上三条公理的基础上，Shapley在理论上证明了能够唯一确定联盟收益的分配向量，即合作博弈中的一种分配形式，则称试φ(F)是博弈的Shapley值。科技创新联盟每个成员获得的公平收益是合作者参与的所有合作贡献的加权平均值。其shapley值为：

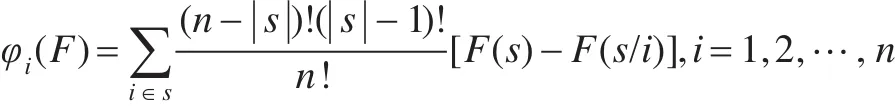
其中|s|为联盟s中所含参与方的个数；s i表示合作联盟s中去掉合作方i；F(s)表示s个成员组建的一体化实体的收益值；φi(F)表示第i个成员从合作中获得的期望分配值。

2.2 实证算例

某水电站的河湾地块防渗工程，为了快速、经济、可靠地提高其深厚松软岩土层的防渗效果，由设计、施工、高校等单位成立了科技创新小组，提出了一种新的帷幕灌浆施工工艺，并在实际灌浆工程中得到了成功的应用。该合作创新项目业主投入科研经费1 000万元（其中成本560万元），科研成果节省工程投资1.6亿元，取得了多项发明与实用新型专利，并研究得到了系列理论成果，通过创新合作实现了“多赢”的目标。然而，在创新过程中，尤其是项目开始到出成果以后，如何分配创新成果的问题，一度困扰着创新小组，并造成了一些合作不愉快，从而影响创新绩效的现象。

现以该工程创新案例为背景，运用Shapley值法来进行创新直接经济的收益分配。所有的收益都估算成经济收益，假定设计、施工、高校都可通过人材技术的引进单独或与另一家单位合作进行此项技术开发，但成本较高。表1是在特定场合单家开发或两家合作以及三家合作开发情况下的收益情况。

表1 合作各方收益情况表

按夏普利值计算：

则在夏普利值法下，设计、施工、高校三方各自可以分得126.7万元，166.7万元，146.6万元。可得初步分配比例 φi(v)=（28.80%，37.88%，33.32%）。

2.3 对Shapley值法的评价与改进

用Shapley值法进行产学研合作的收益分配计算较简单，考虑了多种不同成员与组合的赢利能力，避免了平均分配，联盟成员获取的利益不低于非联盟情况下该成员获取的利益，合理体现了合作共赢的客观情况，调动了合作成员企业的积极性。然而进一步分析就会发现Shapley值法也是有缺陷的，它是假设各种联盟的结合是随机的，结成联盟的成员处于平等的地位，这显然与实际创新联盟情况不一致。技术创新联盟一般有一个牵头单位，各成员的实力与承担的任务也不尽相同，有的对联盟贡献较大，有的对联盟贡献相对较小；有的在创新过程中承担较大的风险，有的成员承担的创新风险较小。联盟成员与组合的赢利能力大小与实际贡献多少并不一定成正比。Shapley值法难以全面体现“多贡献高收益，高风险高收益”的分配原则。因此，在利益分配机制的设计中就要体现联盟成员不同的创新贡献与承担的创新风险。

本文考虑基于各成员的创新贡献与承担的创新风险来对Shapley值法改进，这样才更符合实际情况。文献[12]在采用Shapley值法时，对联盟成员的重要性进行了考虑，通过确定型层次分析法对联盟成员重要性赋以权重，从而进行了一定的改进；文献[10]在采用Shapley值法时，对联盟成员承担的创新风险进行了考虑，利用各方承担的风险因子对收益分配进行了修正；文献[11]采用不确定型层次分析法（AHP）考虑成员对施工投标联合体的贡献，改进Shapley值法来进行投标联合体的利益分配，但其计算比较复杂。为了能够在很大程度上体现专家判断的模糊性和不确定性，更好地反映实际状态，从而使评估结果更具可信性，本文引入FAHP对Shapley值法进行改进，同时考虑创新成员的创新贡献与风险来分析技术创新联盟的利益分配机制。

3 基于FAHP法的联盟成员创新贡献率改进分配法

在任何领域谈到收益分配问题时，首先都要确定收益分配的影响因素。所谓收益分配的影响因素应该是能对收益的产生起贡献作用的因素，本文认为科技创新合作收益分配问题的主要影响因素包括：角色重要性，合作意识，成本投入，企业实力，承担风险。其中成本投入包括资金、人力资源、固定资产、技术、时间等方面，都是可证实的具体合作过程中发生的生产性投入，合同中可以依据市场价格明确规定此类成本对应的报酬，这也是科技创新合作进行时，组建合作实体采用股份制的主要原因和依据。除此之外，创新过程中角色的重要性、合作意识、企业实力、承担风险等很难量化具有相对模糊性。

在利益分配中，实施以贡献率为基准的分配准则，需要解决的关键问题就是如何科学合理地将各成员投入的各种影响收益分配的因素统一量化。本文采用角色重要性、合作意识、成本投入、企业实力、承担风险作为贡献率评价指标，然后再对评价指标采用层次分析法进行赋权以定量确定其相对重要性，并采用模糊综合评价的方法（FAHP）确定各成员综合贡献率，并据此来改进Shapley值分配法。

3.1 评价指标权重计算

请相关专家就角色重要性、合作意识、成本投入、企业实力、承担风险等五个因素的相对重要性进行标度值打分（1～9分制），并构造n=5阶判断矩阵如下[13]：

其中，aij表示第i个指标比第 j个指标的重要程度，aij=1/aji。

据判断矩阵A计算该层次要素关于相邻上一层次要素的优先权重，即为计算A最大特征值所对应的特征向量W=(w1，w2，…w5)T，作为该层次 n个要素的优先权重向量。采用求和法计算特征向量：

（1）将矩阵每一列元素正规化（即使列和为1）

（2）按行求和得权向量：

（3）对向量正规化：

3.2 模糊综合评价创新成员贡献率

模糊综合评价法是根据模糊数学的隶属度理论把定性评价转化为定量评价。

首先对评价因素ui={角色重要性、合作意识、成本投入、企业实力、承担风险}，设评价集V及标准隶属度集V′，即：V=(v1，v2，…，v5)={无，低，较低，中等，较高，高}，并赋予评价集各元素以量值V′={0，1，3，5，7，9}。

然后构造评判矩阵，由专家结合创新贡献实际情况进行隶属度打分。设对第i个评价因素ui进行单因素评价得到一个相对于vj的隶属度rij，这样就得到第i个因素的 ui的单因素评判集：ri=(ri1，ri2，…，rin)，因此，m个单因素的评价集就构造出一个总的隶属度矩阵R：

最后对每一个评价因素进行模糊综合评价即：P=W ×R 。归一化处理得 P*=(λ1，λ2，…，λn)，即得各创新成员综合贡献率λi。

3.3 对Shapley值分配法进行改进

Shapley值利益分配方法假定各成员的投入和承担的风险相等，但实际情况并不是如此，因此需要运用贡根据贡献率的利益分担比例与平均分摊的差值，其中。当∆λi≥0时，表示联盟成员在实际合作中投入的资源和承担的风险比平均水平高，因此在联盟利益分配中应该给其正的补偿。同理，当∆λi≤0时，表示联盟成员在实际合作中投入的资源和承担的风险比平均水平低，则应从原先分配取得的利益中扣除部分所得[15]。则考虑创新成员综合贡献率λi对Shapley值分配法进行调整，得最终分配值：

3.4 案例计算与分析

仍然采用第2章防渗帷幕灌浆新工艺科技创新的案例。由科技创新联盟专家委员会对科技创新中角色重要性、合作意识、成本付出、企业实力、承担风险等因素进行两两比较打分，建立判断矩阵A。

对矩阵A进行权向量W计算见表2。

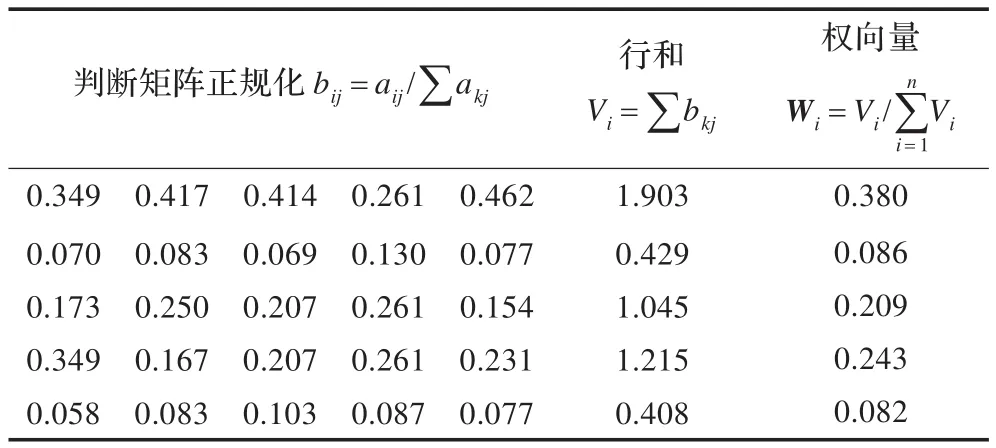
表2 权向量W的计算表

求得W=(0.380 0.086 0.209 0.243 0.082)T，其每一个向量表示创新贡献因素角色重要性、合作意识、成本付出、企业实力、承担风险等的相对权重。再由了解本工程实际创新过程的专家针对设计、施工、高校三方的实际贡献对各因素隶属度打分得隶属度矩阵R。

则各创新单位的实际贡献率矩阵为：

经归一化处理后得到创新贡献与风险分配因子P*=（0.25，0.35，0.40），即设计、施工、高校创新贡献率与风险因子分别为 λ设计=0.25，λ施工=0.35，λ高校=0.40。

运用创新贡献率与风险因子对Shapley值进行调整，结合前面初步分配比例φi(v)=(28.80%,37.88%,33.32%)，则最终分配比例：

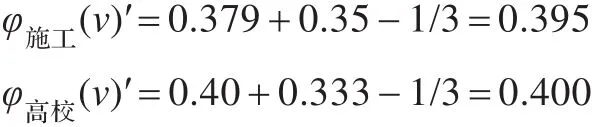
则创新总获益440万按创新联盟贡献率与承担风险改进的Shapley值获益分配分别为：

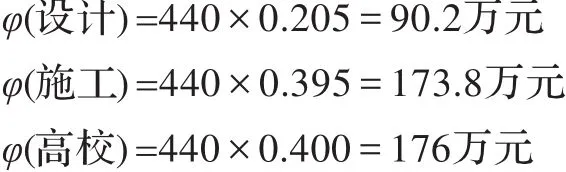
与直接采用Shapley值法分配结果对比，可以发现：设计单位的分配额相对于单纯使用Shapley值法分配有所下降，而施工单位和高校有所上升。从该案例的创新实际来看，该项目的核心创新内容与创新风险大的环节都由高校承担，施工企业将创新成果在施工现场进行验证实施，设计企业主要提供工程背景资料和相关规范标准。因此改进后的分配方案才是符合客观实际的。这是因为Shapley值法只是从成员加入联盟前与加入联盟后的联盟收益对比来考虑联盟内的利益分配，这种纯粹以表面数字变化为依据的分配机制存在不足，它忽略了产生这种数字变化的专业背景和创新实际贡献率，不符合工程技术创新的特点，缺乏足够的信服力。若按此分配准则，恐很难激励创新联盟的积极性，这对三家参与单位而言都是不利的。而利用FAHP基于创新贡献改进分配方法后，充分肯定了不同成员在联盟中的价值：首先，相对重要的成员，担任创新核心任务的高校获取的利益明显要高于原分配结果，这是因为其承担的风险最大且科研实力最强；其次，在联合体中投入有形资源较多和专业施工能力较强的施工单位分配的利益也略有增加；最后，设计单位分配的利益虽比原来有所下降，但仍比其单独创新要高，对其显然是有利的，设计单位仍然会有合作创新的动力。

4 结语

科技创新联盟中的各成员通过各展所长，相互配合，对创新项目承包实现内部优化组合，可以降低创新成本，提高创新效率和利润，还可以有效地分散创新风险。但通过联合创新的收益如何进行合理分配，对于调动各方创新的积极性至关重要。本文从合作博弈的角度，将Shapley值法用于创新联盟的收益分配研究，并提出包含联盟成员创新贡献与风险承担的评价指标，采用模糊综合评价法（FAHP）对成员创新贡献赋以权重从而改进Shapley值法，合理地提高了核心创新单位和承担风险大的单位的收益分配，分配结果与成员在联盟中的价值相匹配。希望通过研究合理的利益分配机制，推动更多科研创新企业各取所长组建创新联盟，增强和提高企业的创新活力和竞争力，为工程技术创新联盟的稳定发展，获得更高的创新收益提供理论依据。本方法的不足之处在于计算过程相对较复杂，对于不同的工程项目，随着创新成员数量和评价指标的增多，计算量将更大，如能将分析过程实现可视化编程，利用计算机进行计算，就能更准确高效地推广应用本方法。

[1]牛晓霞.基于博弈的校企合作技术创新过程研究[D].西安：西安理工大学，2005：2-4.

[2]傅家骥.技术创新学[M].北京：清华大学出版社，1998：8-10.

[3]宋伟.论科技经济结合对社会进步的作用[J].科学学研究，1995（4）：35-38.

[4]Emelichev V A，Kuzmin K G.Stability radius of an efficient solution of avector problem of integer linear programming in the Gölder metric[J].Cybernetics and Systems Analysis，2006，42（4）：609-614.

[5]Immorlica N，Kleinberg J，Mahdian M，et al.The role of compatibility in thediffusion of technologies through social networks[C]//Proceedings of the 8th ACM Conference on Electronic Commerce.New York，USA：ACM，2007：75-83.

[6]Guardiola L A，Meca A，Timmer J.Cooperation and profit allocation indistribution chains[J].Decision Support Systems，2007，44（1）：17-27.

[7]张捍东，严钟，方大春.应用ANP的Shapley值法动态联盟利益分配策略[J].系统工程学报，2009，24（2）：205-210.

[8]生延超.基于改进的Shapley值法的技术联盟企业利益分配[J].大连理工大学学报：社会科学版，2009，30（2）：34-39.

[9]杨晶，江可申，邸强.基于TOPSIS的动态联盟利益分配方法[J].系统工程，2008，26（10）：22-25.

[10]鲍新中，刘澄，张建斌.合作博弈理论在产学研合作收益分配中的应用[J].科学管理研究，2008（5）：21-24.

[11]易欣，张飞涟，邱慧，等.不确定AHP和Shapley值应用于投标联合体利益分配[J].计算机工程与应用，2012，48（27）：194-199.

[12]王鹏，陈向东.基于改进夏普利值的物流企业战略联盟利益分配机制研究[J].统计与决策，2011（12）：47-50.

[13]吴恒安.社会评价和水利项目社会评价[J].海河水利，1997（4）：135-137.

[14]郝海，踪家峰.系统分析与评价方法[M].北京：经济科学出版社，2007.

[15]苏秋来.产业技术创新联盟利益分配研究[D].泉州：华侨大学，2012：40-41.