基于多代理分散式控制的智能电网存储管理

王丽君，蔚承建，胡恒恺，王 开，刘 凯

WANG Lijun1,WEIChengjian1,HU Hengkai1,WANG Kai2,LIU Kai3

1.南京工业大学 电子与信息工程学院，南京 210009

2.东南大学 信息科学与工程学院，南京 210018

3.解放军理工大学 国防工程学院，南京 210007

1.College of Electronics and Information Engineering,Nanjing University of Technology,Nanjing 210009,China

2.Department of Information Science and Engineering,Southeast University,Nanjing 210018,China

3.Defence College of Engineering,PLA University of Science and Technology,Nanjing 210007,China

智能电网，又被称为电网“高速公路”，是当今国际最前沿的新能源产业之一，已成为各国争相研发的热点。智能电网发展的一个显著特征是储能设备的应用，储能设备可以降低用户对于峰值电力的需求，减小电力需求的波动。因此在智能电网中，储能设备是实现智能电网的重要基础之一[1-3]。

智能电网的另一个重要组成部分是智能电表。智能电表可以获取当前电网中各电力供应商的信息，从而有效地管理家庭或公司的用电设备，节省用户的用电花费。在智能电网中，电价随着用户需求不断动态变化着，电价与用户需求形成拟线性关系，即需求越大电价越高。储能设备在用电高峰期为用电设备供应电能，降低用电高峰期对电力发电机组的需求，从而可以降低能源成本和CO2的排放量。然而，如果大量的储能设备在同一时刻接入电网进行充电，将会使电网负载过大，导致用户花费提高及CO2排放量的增大，甚至有可能会损坏当前电网。因此，如何对储能设备进行有效的管理是关键问题所在。

多代理系统（Multi-agent Systems，MAS）模型作为分析系统性能的基本方法已受到很多研究者的关注[4-5]，多代理技术被普遍认为是管理和控制智能电网的一个有效途径。随着可以监视和控制家庭设备的智能电表的出现，软件Agent可嵌入到智能电表中作为家庭或公司用电设备的控制管理者。在当前的电网中，基于Agent技术的存储管理应用还比较少。目前只有间歇性发电设备（如太阳能发电，风能发电）使用了大型的电力存储设备[6]。首先考虑智能电表优化家庭电力使用的是Daryanian[7]，他考虑了家庭储能设备的管理方法；Houwing[8]提出了基于Agent技术的热电联供设备的优化算法；Vandael[9]利用MAS模型管理了混合动力汽车的储能设备；Vytelingum[10]研究了基于代理的智能电网微存储管理，提出了一种依据市场预测价格自适应学习的存储策略，使得实际存储策略接近最优存储策略，社会福利显著提高。但其中Agent只采用了简单的学习策略，而没有考虑Agent之间的交互问题，所以鉴于智能电网对未来低碳经济的重要性，本文进一步发展了Vytelingum的研究工作，提出来Agent更有效的学习策略，并考虑了Agent之间的相互学习，使得存储策略更加逼近于最优存储策略，社会福利最大化。

1 模型描述

将每天分成T个固定时间段。每天，Agent从电力供应商买入电量、储能设备存储电量。Agent集合的用电需求将会呈现出一种规律变化模式。下面具体描述Agent及相应市场模型。

1.1 Agent描述

设用户Agent集合为 A，一天的时间段集合J={1,2,…,T}，一般可将T设为48，即每半小时为一个时间段。Agent的目标是最小化用户的用电成本。假设Agent a∈A有一个基本固定的使用电量需求组合求。对于Agent a，储能设备的最大储电容量为cam，存储效率为 μa，单位电量存储成本为ma，即如果储能设备充入q电量，但只能释放出μaq电量，用户花费的存储成本为maq。

Agent代表自利的用户，目标是最小化用电量成本，因此需要优化储能设备的当日存储策略

1.2 电力市场模型

在电力市场模型中，主要考虑市场当中的价格机制，以及用户的存储策略。在此电力市场模型中，电力价格是由市场的总体电力需求决定的，所以需求的改变会直接影响市场中电价的变化。而家庭用户的用电需求存在共同特性，如用户在夜间用电量较少，而在傍晚的用电需求则会达到峰值，同时由于家庭用户用电量存在周期性。根据这些特性，假设电力市场中用户每日平均用电需求如图1所示。

本文主要目的在于研究Agent自适应策略对于Agent本身以及系统的影响，因此在这里首先定义社会福利标准。

负载系数：用一天的48时段平均用电量比上当天峰值的用电量，理想值为1，较低的负载系数表明当前系统中含有较高的峰值用电量。

排碳量：在发电中会产生大量的CO2，这里用生产每度电（kWh）所产生的CO2来描述排碳量，理想值越低越好。每度电含碳量与电力总需求成正比关系，当电力市场中的总需求增大时，生产每度电所排出的CO2也相应提高。

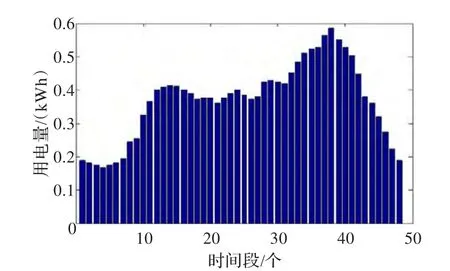
图1 用户平均用电需求

2 最优存储策略

在电力市场中，电价根据市场的总电量需求和供给决定的[10-11]。本文假设电价与用户购买总电量成简单的线性正比关系。根据家庭用户普遍的用电特征，假设1天为周期性的用电情况，因此可以将1天作为一个研究周期，Agent的最优存储策略就是使得用户一天花费成本（实际使用电量成本和存储成本）最小的策略。

为了计算最优存储策略，假设Agent完全掌握市场信息，即Agent a掌握了其他Agent a′∈A的私有信息，即Agent a′的用电量、存储效率单位电量存储成本 ma′、存储容量。同时每个Agent掌握了用电价格与用电量的关系。用户在时间段 j电价可以定义为：

Agent a一天花费总成本等于各个时间段 j用电成本的总和，即：

其中ba表示Agent a的存储策略组合，表示使用储能设备的使用成本。

在这里，需要对Agent的电量存储策略做进一步的说明。用户每天负载的实际用电量基本上是保持不变的，为了最小化每天的用电成本，其储能设备每天的总充电量乘以存储效率等于总放电量，即并且用户一天的实际用电量经历一个高低变化的循环过程，从而可以合理地估计，作为容量有限的储能设备，也一定会经历充放电的循环过程。

在将Agent最优存储策略数学化描述之前，先介绍一下纳什均衡的概念。纳什均衡[12-13]：假设有n个局中人参与博弈，在给定其他人策略的条件下，每个局中人都选择自己的最优策略（个人最优策略可能依赖于也可能不依赖于他人的策略），从而使自己利益最大化。所有局中人的策略构成一个策略组合（Strategy Profile）。纳什均衡指的是这样一种策略组合，这种策略组合是由所有局中人的最优策略组成。即在给定别人策略的情况下，没有人愿意打破这种策略组合（均衡状态），在此状态之下，任何一个局中人单方面改变自己的策略都不会使自己的利益增大。

在电力市场中，用户电价 pj是由所有用户在时间段 j的总购买的电量决定的。因此agent a的用电成本依赖于其他Agent的存储策略，而所有Agent都会选择使自己用电成本最小的存储策略，由于市场信息是完全透明的，即每个Agent都掌握了其他Agent的私有信息，因此每个Agent都会根据其他Agent的策略选取最优存储策略即满足纳什均衡时的存储策略，式（5）的多目标函数定义了Agent的最优存储策略。

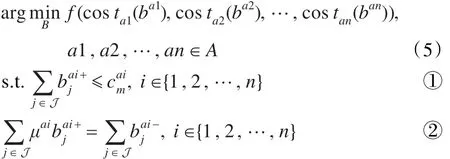
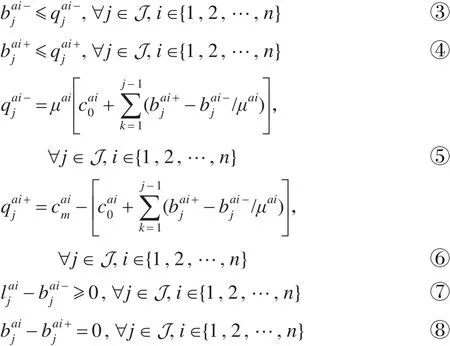
B={ba1，ba2，…，ban} 是 Agent的 存 储 策 略 集 合 ，costai(·)在公式（4）中定义，表示储能设备初始剩余电量，且式中所有变量大于等于0。约束①表示充电量不得超过储能设备容量；约束②表示一天的充电量必须全部用完；约束③表示每一时间段的放电量不超过当前时刻储能设备的剩余电量；约束④表示每一时间段的充电量不超过允许最大充电容量；约束⑤表示每一时间段的储能设备剩余电量；约束⑥每一时间段的储能设备可充电量；约束⑦考虑了用户不可以向电力市场卖电；约束以同时充电与放电。从上述优化目标函数以及限制条件，就可以计算出最优存储策略bai*以及最优的存储容量cai*。

3 电力市场的ZIPML Agent

在上述计算最优存储策略的时候，假设每一时间段j的用电量和电价都是已知的，然而在电力市场中用户在时间段 j的实际电价需要Agent预测。所以Agent必须通过学习算法不断优化自己的存储策略，从而使得存储策略逼近最优存储策略。学习算法的有效性将直接决定Agent在电力市场中的表现。因此本文基于CDA市场中ZIP Agent[14]的学习策略，提出了适应电力市场的ZIPML Agent用于储能设备的管理。

3.1 ZIPML Agent最佳存储策略

针对实际电价需要Agent预测，且在每天同一时间段 j的电价随着用户实际购买电量的变化（由于用户使用储能设备导致）而不断变化，本文所考虑的存储策略是基于前一天市场的最优存储策略，Agent首先需要预存储容量。

Agent a的目标是根据预测价格 pa和固定使用电量la优化下一天的最优存储策略ba，最优化成本函数如下：

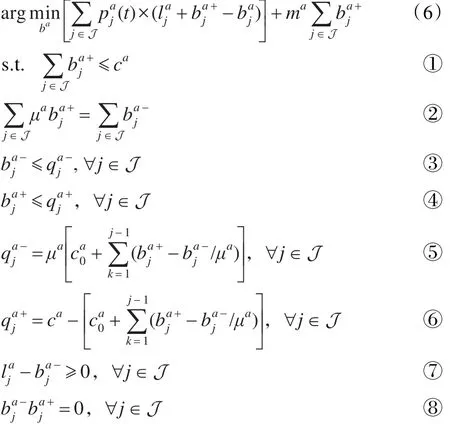
由于市场的价格不断改变，Agent每天也必须不断改变其存储容量。同时由于储能设备存在使用成本要通过学习以更好地适应市场，降低花费。在这里用ca表示Agent经过学习后的实际存储容量上界，即式（6）中 ca满足，其中 t表示Agent学习的天数。

3.2 单Agent学习

首先考虑Agent存储策略的学习，Agent需要根据优化的当前最优存储策略式（6）算出）自适应调整实际存储策略。基于CDA市场下的ZIP策略提出了适应电力市场的ZIPML策略。具体存储策略自适应学习算法形式如下：

3.3 多Agent相互学习

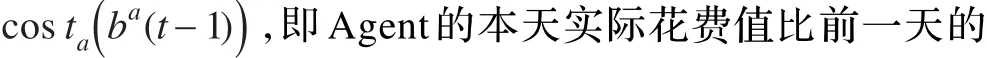
4 实验分析

根据英国用户平均用电需求，使用java程序编写了存储代理模拟器，用于模拟代理策略对于电力价格及自身利益的影响。为了验证自适应学习算法的有效性，实验模拟了1 000个Agent 100天内的存储策略变化趋势。参照了用户平均用电需求，根据图1设置用户电力需求。同时假设Agent在未采用储能设备时每日具有相同的基本固定用电需求(∀ j∈J )，单位电量存储成本ma=0.1，存储效率 μa=0.95，学习系数 λa∈[0 .05，0.1] ，冲量系数γa∈[0 .3，0.6]，初始剩余电量设置为0.5 kWh，初始最大存储容量(0)设置为5 kWh，初始存储策略)(∀ j∈J) 设置为0 kWh。

为了简化纳什均衡的计算首先考虑由1 000个同质Agent组成的系统，其中每个Agent的固定用电需求都如图1所示。由于所有Agent都有相同的私有信息，因此式（5）中所有子目标 cos ta(·)完全相同，式（5）可由多目标优化问题转化为一个二次优化问题。根据上述设置，首先算出系统的纳什均衡，图2给出了纳什均衡策略，其中大于0的部分表示给储能设备充电；小于0的部分表示储能设备放电。从图中可以明显看出，Agent在夜间（低电价）存储电力，在傍晚（高电价）使用存储的电力。

图2 最优存储策略

图3表示了其中一个Agent在100天内的存储策略变化趋势，可以看出在100天的时候实际存储策略已经非常逼近最优存储策略。可以看出Agent经过30天的自适应学习以后已经接近最优存储策略，随着学习天数的增加，与最优存储策略更加逼近。在市场交易末期最大存储容量收敛于1.7 kWh。这就表明对于一般用户，只需要容量为2 kWh的储能设备就可以很好地优化管理用电需求。开始逼近最优用电成本，并收敛于最优成本，而在第100天的时候最优用电成本与实际用电成本相比已达到了99.98%。图7和图8显示了系统的社会福利，第10天时碳排放量已经明显减小，100天后碳排放量已减少至原来的93.6%。负载系数也由初始状态下的66%上升至92%，这表明当前系统中用电需求量已经达到平坦状态，起到了削峰的效果，从而增加了电网的可靠性，提高了电网的使用效率。

图5 系统价格

上述实验表明，ZIPML策略可以快速有效地逼近纳什均衡策略。有了这个性质之后，需要对ZIPML策略的有效性进行研究，假设系统中每个Agent有着各不相同的固定用电需求，在这里用电需求的设置为符合图1的正态分布。其中50%的Agent使用Vytelingum提出的学习策略，50%的Agent使用ZIPML学习策略。

这里通过用户节省花费的百分比来检验策略的有效性。从图4中可以看出在当前的系统环境设置下，随着时间的推移，第10天以后ZIPML Agent则可以更加有效地节省用电花费；最终ZIPML Agent可以为用户节省6.1%的花费，优于Vytelingum Agent的5.6%。

图4 ZIPML策略与Vytelingum策略比较

最后对于社会福利进行分析，研究在纳什均衡状态下，系统的集体利益是否被破坏[15]。系统中1 000个Agent的总体需求，用电需求的设置为符合图1的正态分布。图5中可以看到，随着天数的增加，电价渐渐趋于平稳，30天后系统的电价已经接近平坦状态。图6显示了用户总用电成本与最优值的比较，Agent存储策略经过25天左右的自适应学习以后，实际用电成本已

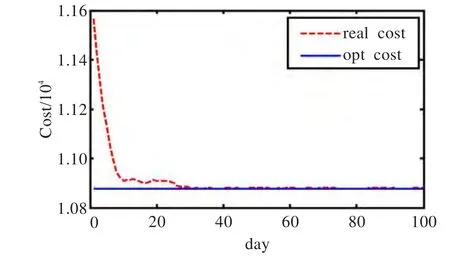
图6 系统总成本

图7 排碳量减少曲线图

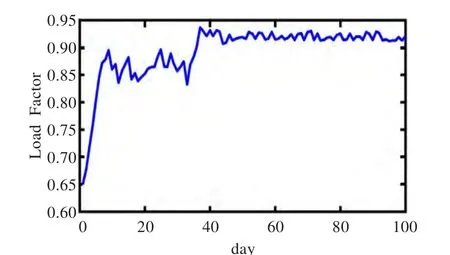
图8 负载因素

5 结论

鉴于智能电网对未来低碳经济的重要性，本文在Vytelingum的研究工作基础上，考虑了Agent之间的相互学习，在此基础上提出了更有效的基于多Agent技术的ZIPML算法，使得实际存储策略逼近最优存储策略。通过模拟实验得出，ZIPML Agent相比于Vytelingum Agent可以更加有效地节省用电花费，约节省6.1%。用户实际存储策略经过一段时间后逐渐逼近最优存储策略；系统总成本也逼近于最优值。负载因素逐渐逼近于1，即电网高峰期的负荷得到有效降低，排碳量也有明显减少，验证了该算法的有效性。

[1]U S Department-Of-Energy.Grid 2030：a national vision for electricity's second 100 years[EB/OL].（2003-02-01）.http：//www.ferc.gov/eventcalendar/files/20050608125055-grid-2030.pdf.

[2]Galvin R，Yeager K.Perfect power：how the micro grid revolution will unleash cleaner，greener[M].[S.l.]：More Abundant Energy.McGraw-Hill Professional，2008.

[3]MacKay D.Sustainable energy：without the hot air[M].[S.l.]：UIT Cambridge，2009.

[4]Exarchakos L，Leach M，Exarchakos G.Modelling electricity storage systems management under the influence of demandside management programmes[J].International Journal of Energy Research，2009，33（1）：62-76.

[5]van Dam K H，Houwing M，Bouwmans I.Agent-based control of distributed electricity generation with micro combined heat and power cross-sectoral learning for process and infrastructure engineers[J].Computers &Chemical Engineering，2008，32（1/2）：205-217.

[6]Korpaas M，Holen A T，Hildrum R.Operation and sizing of energy storage for wind power plants in a market system[J].International Journal of Electrical Power&Energy Systems，2003，25（8）：599-606.

[7]Daryanian B，Bohn R，Tabors R.Optimal demand-side response to electricity spot prices for storage-type customers[J].IEEE Transactions on Power Systems，1989，4（3）：897-903.

[8]Houwing M，Negenborn R R，Heijnen P W，et al.Least-cost model predictive control of residential energy resources when applying chp[M].London，UK：Power Tech，2007：425-430.

[9]Vandael S，Boucke N，Holvoet T，et al.Decentralized demand side management of plug-in hybrid vehicles in a smart Grid[C]//Autonomous Agents and MultiAgent Systems（AAMAS 2010），Toronto，Canada，2010.

[10]Vytelingum P，Voice T D，Ramchurn S D，et al.Agent-based micro-storage management for the smart grid[C]//Autonomous Agents And MultiAgent Systems（AAMAS 2010），Toronto，Canada.，2010.

[11]Williams J，Wright B.Storage and commodity markets[M].UIT，Cambridge：[s.n.]，1991.

[12]Osborne M J.An introduction to game theory[M].[S.l.]：Oxford University Press，2003.

[13]Weibull J W.Evolutionary game theory[M].Cambridge，MA：MIT Press，1995.

[14]Cliff D，Bruten J.Minimal-intelligence agents for bargaining behaviors in market-based environments，Technical Report HPL-97-91[R].1997.

[15]Holland A.Welfare losses in commodity storage games[C]//Proceedings of The 8th International Conference on Autonomous Agents and Multiagent Systems，Budapest，2009：1253-1254.