基于混合遗传算法的多巷道间移动拣选优化

张海军，张 博，岳溥庥，郭 风

ZHANG Haijun,ZHANG Bo,YUEPuxiu,GUO Feng

北京物资学院 信息学院，北京 101149

School of Information,Beijing Wuzi University,Beijing 101149,China

1 引言

仓库拣选作业是企业中最为频繁的生产活动之一，采购入库的商品、配件需要仓库作业人员分门别类地放置在货架上，出库的一单商品、配件需要作业人员从货架中取出。许多大型仓库、配送中心采用高层货架式立体仓库，相邻两排货架之间有一条巷道，每条巷道有一台堆垛机，堆垛机可以同时沿垂直方向和水平方向移动，存取巷道两侧垂直货架上的货物，如图1所示：0点为巷道出入口，a、b、c、d、e、f为垂直货架上的几个取货点，堆垛机一次可以拣选若干个货位上的货物，然后返回到0点将货箱放置到传送系统上。以往的研究主要是针对堆垛机在单一巷道内垂直货架上的拣选作业进行优化，刘臣奇等[1]提出一种蚁群算法，对取货点的存取顺序进行优化，以使得作业时间最短。但是，该方法假定堆垛机一次作业可以拣选所有取货点的货物，没有考虑堆垛机所携带的货箱的容量限制，针对这一问题，常发亮等[2]提出一种遗传算法，在堆垛机一次作业容量受限的情况下，针对垂直货架上的多个取货点，安排若干次拣选作业使得总的拣选代价最小（如图2所示），图2中表示两次拣选作业，第一次的拣选顺序为0-a-e-f-0，第二次拣选顺序为0-b-c-d-0。对于堆垛机需要行进到其他巷道中进行拣选的问题，该方法不能够解决，当然，对于自动化立体仓库，一般每个巷道都有一台堆垛机，负责拣选该巷道两侧货架上的货物，某一巷道的堆垛机不需要行进到其他巷道进行拣选。但是，在某些情况下，需要一台堆垛机拣选多个巷道中的货物，李梅娟等[3]对此问题进行了研究，如图3所示，堆垛机从0点出发，依次拣选巷道1、巷道2、…、巷道 j两侧货架中的货物，而后返回到0点，在拣选过程中，堆垛机所携带的货箱容量有限，装满一箱货物就返回到0点把货物放置到传送系统上，并且，前一巷道的拣选作业全部完成后才能进入下一巷道进行作业。以上这些方法主要优化的是堆垛机在垂直高层货架中取货时在垂直作业面上的移动距离。

图2 巷道堆垛机在垂直货架上的两次存取作业示意图

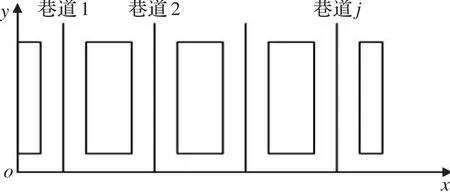
图3 堆垛机在多巷道中拣选俯视图

对于需要在多个巷道间移动拣选，拣选作业需要优化的主要是拣选作业人员水平移动距离的情况下，以上的方法都不适用。例如超市、网店、书店、药店以及需要堆垛设备在多巷道间移动拣选的立体仓库的补货发货作业。本文是对这种情况下的订单拣选进行优化，以指导工作人员沿最短的拣选路线进行作业以节省拣选时间和拣选费用。图4为这种情况下仓库俯视示意图，图中标记了某一订单所涉及到的25个货位，每个货位取货量不一，拣选设备的容量有限，如何安排拣选作业，使得这个订单总的拣选路线最短。

本文的主要创新点有：第一，针对多巷道中移动拣选问题，通过引入节点来减少直接计算各货位间最短路径的计算量。第二，使用混合遗传算法结合Lin-Kernighan算法来实现订单拣选的优化，实验结果表明，该算法优于粒子群优化算法。

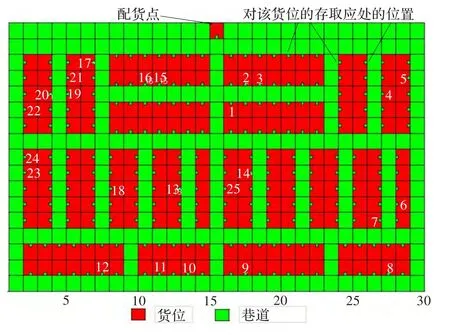
图4 仓库俯视示意图

2 拣选路径优化的数学模型

假设某一订单涉及到需要拣选的货位数为n个，货位编号从1到n，编号为0代表配货点。第i个货位点的需求量为qi，拣选设备的容量为Q，任一个货位点的需求量都不大于拣选设备的容量Q。由此可知，该订单所需拣选作业次数不超过n，假设需要n次拣选作业，每次拣选作业使用同样的容量为Q的拣选设备。文献[4]所给出的数学模型中拣选作业次数没有明确指定，不利于对问题的理解，借鉴文献[4]给出的模型，建立了以下数学模型见公式（1）~（9）。

其中cij为从货位i到货位 j的旅行距离。=1表示第v次拣选作业将先访问货位i而后紧接访问货位j，即i和 j之间构成第v次拣选路线中的一边，否则，=0。q为货位i的需求量；Q为第v次拣选作业的iv可载容量。式（1）表明了优化目标是总的拣选路径最短。约束（2）、（3）表示每个需求点必须且只能被拣选一次。约束（4）表示每次拣选作业经过的路线必须是连续的，即某次拣选作业到达某个需求点时也必须离开这个需求点，并且最终构成一个拣选回路。约束（5）表示每次拣选作业所服务的需求点的总需求量不超过该次拣选设备的容量。约束（6）表示每次拣选作业所使用的拣选设备容量相同，都为Q。约束（9）表示每次拣选作业消，也即总的实际的拣选次数小于n。从模型可以看出，此问题是一个NP-hard问题，需要寻求启发式的方法来解决。

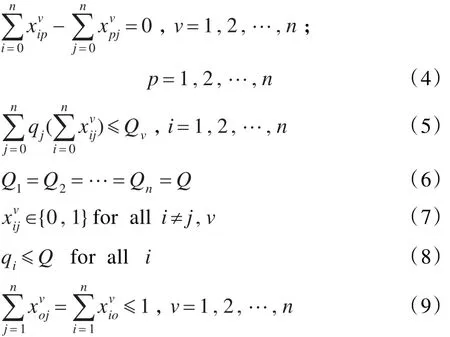
3 仓库平面布置图的数据存储及需求点间路径计算

仓库的主要元素可以分为：巷道、货位、节点、障碍物。巷道是存取商品的供拣选作业人员行走的通道，假定只有纵向和横向两种直线巷道。节点是纵向巷道和横向巷道的交叉点。货位是存储货物的单元，存取这个货位中的货物必需在特定的位置，有的货位取货位置在它靠近的左边巷道，有的在位于其右侧的巷道，有的在其他巷道。为了生成并存储这些元素的信息，把仓库平面分成若干行和列，行列交叉位置为一仓库单元格，这个仓库单元格可以是一个巷道单元也可以是货位单元，因此，需要“仓库单元格”这样的一种数据结构来记录每个仓库单元格的信息，它是一个矩阵，矩阵的第m行第n列的元素值为1，表示仓库的第m行第n列的单元格为一货位，并且取货位置在上方巷道；值为2表示为货位，取货位置在下方巷道；值为3表示为货位，取货位置在左边巷道；值为4表示为货位，取货位置在右边巷道；值为5表示此单元格为一巷道单元；值为6表示为一障碍物单元。可以以图形化的界面让用户确定仓库各单元的信息。

“仓库单元格”矩阵记录下了每个仓库单元的信息，由此可以计算出所有的货位、巷道和节点。一个巷道上的两个相邻的节点为邻接节点，如图5所示，E与C、C与 A、A与 B、B与 D、D 与 F、F与 E、C 与 D、C 与G、G与H互为邻接节点。先计算出邻接节点间的最短距离，构成节点邻接矩阵，邻接节点间的最短距离是这两个节点在同一巷道中相隔的仓库单元的数量，如A和B这两个邻接节点的距离为6，邻接矩阵中的第i行第 j列的值k如果不为无穷大，则表示第i个节点与第 j个节点邻接，且它们之间拣选距离为k。由于节点的数量不大，可以在节点邻接矩阵的基础上用Floyd算法[5]计算出所有节点间的最短距离，并存储这个所有节点间的最短距离矩阵以及相应的路径信息。

一个货位的取货点是巷道上的一个单元，如图5所示，货位13、14的取货点为其紧邻的右侧巷道上的巷道单元，货位25的取货点是其紧邻的左侧巷道上的巷道单元。一个货位最多有两个与其邻接的节点，如图5所示，货位13的邻接节点是E和F，货位14的邻接节点是 A和 B，货位25的邻接节点是C和 D，货位1、2、3的邻接节点是G和H。在计算任意两个货位之间的最短拣选距离时，把这两个货位的邻接节点间的最短距离再加上货位到其邻接节点的最短距离即可得到这两个货位之间的最短拣选距离（如果这两个货位的邻接节点相同，则直接计算这两个货位间的欧氏距离即可）和拣选路径。如图5所示，要计算货位1和14之间的最短拣选距离，可以借助货位1的两个邻接节点G和H与货位14的两个邻接节点A和B之间的交叉距离，具体计算见公式（10）：

其中Dist(i，j)表示i与 j之间的最短距离，任意两个节点间的最短距离已经事先计算了出来，货位与其邻接节点的最短距离也很容易求得，因此，公式（10）计算量不大。在计算一个订单所涉及的货位之间的最短距离时，可以临时计算。

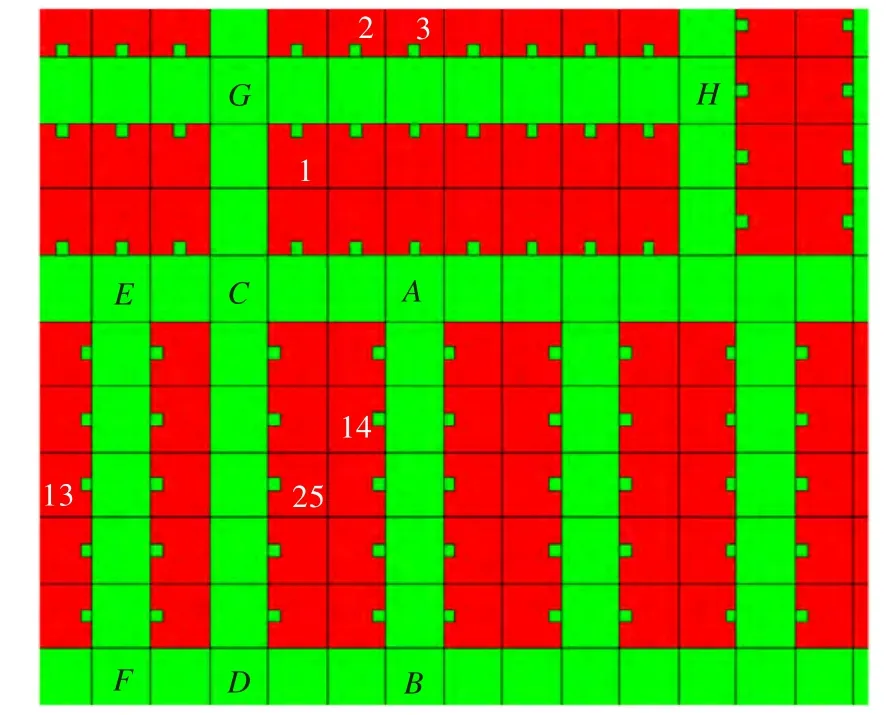
图5 货位邻接节点示意图

4 遗传算法求解订单拣选路径

遗传算法（Genetic Algorithm，GA）是Holland教授[6]最早提出的，是求解复杂组合优化问题的有效方法，典型的遗传算法主要包括选择、交叉、变异三个基本的遗传算子，其中交叉操作是遗传算法的主要搜索手段，是影响算法收敛性及搜索效率的关键因素，常用的交叉操作有单点交叉和双点交叉，双点交叉能更有效地离散杂交子代群体，更有利于寻找到最优解[7]，因此，采用双点交叉的交叉运算。在染色体适应度值的计算以及重插入的操作中，使用了文献[8]中所讲述的英国设菲尔德（Sheffield）大学的MATLAB遗传算法工具箱中的有关函数。

4.1 编码方案的确定

定理1假设拣选设备容量为Q，一个订单所涉及的需求点个数为n，每个需求点的需求量不大于Q，总的需求量为P，则使总拣选路径最短的拣选作业次数K满足公式（11）：

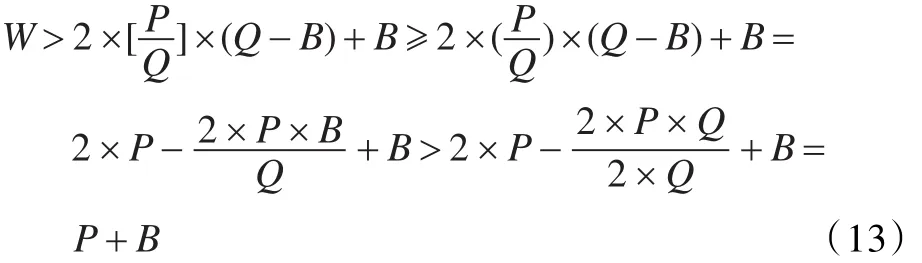
而总的需求量为P，总的拣选量W不可能大于P＋B。因此，肯定存在某一拣选作业 j的载货量不大于Q-B。那么可以把拣选作业i的最后一个需求点与作业 j的第一个需求点连接，合并拣选，将得到更短的拣选路径。

另一方面，需求点的个数为n个，每个需求点的需求量不大于Q，因此，最优拣选次数K不超过n。而显然的，得证。

假设拣选设备的容量为Q，某订单所涉及的需求点为n个，这些需求点的总需求量为P。由定理1得，过引入K-1个虚拟需求点（即配货点Depot，它的货位编号设为0）来构造一个染色体。假设Q=100，n＝8，该订单所涉及到的需求点的货位编号为“138，4，9，330，40，30，55，149”，这8个货位各自取货量分别为：64，34，14，29，16，27，12，3。可计算得 K=5，即需要4个虚拟需求点。用自然数列“1，2，3，4，5，6，7，8”代表这8个货位，用9，10，11，12代表4个虚拟需求点。形如“10，1，2，8，9，6，3，12，11，5，4，7”的染色体表示进行了三次拣选作业，这三次拣选作业的拣选路线分别为：“0-138-4-149-0”，“0-30-9-0”和“0-40-330-55-0”。在将一个染色体映射到一个订单的多个拣选作业时，染色体的首尾视为各存在一个虚拟需求点，表示从配货点出发以及返回到配货点，另外，将两个及两个以上的连续的虚拟需求点视为一个虚拟需求点。按照此编码方案，通过引入K-1个虚拟节点，可以涵盖拣选次数从1到K的该订单的可能的拣选情况。由定理1可知，染色体的长度确定为L=n+K-1，它所形成的L维空间涵盖了最优解空间。引入更多的虚拟点也即假设更多的拣选作业次数只会扩大问题的维数，增大无用的搜索空间，不利于提高解的质量和收敛速度。

4.2 初始种群的确定

以上面的订单为例，该订单涉及到货位编号为“138，4，9，330，40，30，55，149”，把其映射到1~8的8个自然数，而后再加入 4个虚拟节点9，10，11，12，随机产生1~12这12个整数的一个排列，这个排列即为一个个体。设种群规模为N，则随机产生N个这样的个体，即形成初始群体。

4.3 适应度计算

以个体“10，1，2，8，9，6，3，12，11，5，4，7”为例，它表示的拣选路线分别为：“0-138-4-149-0”，“0-30-9-0”和“0-40-330-55-0”。这三次拣选作业各自的拣选量分别为：64+34+3=101，27+14=41和 16+29+12=57，可以看到，由于拣选设备的容量Q=100，第一个拣选作业超过了拣选设备的容量，定义一个惩罚系数Pe=100来对违反拣选设备容量约束的情况进行惩罚，假设这三次拣选作业的总的行走距离为D，则该染色体的函数值为Fv=D+(101-100)×100，这个函数值越大，适应度值越小。为了避免较优的个体迅速繁殖而使得遗传算法过早收敛，这里采用基于函数值从小到大线性排序来计算适应度的方法。种群中最小函数值的个体适应度为2，最大距离的个体适应度为0，假设一个个体 j的排序为Pos，种群大小为N，则其适应度为：

4.4 选择操作

采用赌轮选择法产生下一代90%的个体。首先计算上代群体中所有个体适应度的总计算每此作为其被选择的概率。然后，采用赌轮选择法选择相应的个体进入下一代。这里，设置代沟为0.9，即每一代中有10%的最优个体直接复制到下一代中。

4.5 交叉操作

新个体进行两两配对，按交叉概率Pc进行双点交叉重组。

（1）随机在两个个体中选择一个交配区域，如两个个体及交配区域选定为：A=“10，1，2，|8，9，6，3，12，|11，5，4，7”，B=“5，7，2，|1，4，8，6，3，|11，12，9，10”，其中两个“|”之间的部分为交配区域。

（2）将A和B的交配区域交换，得：A′=“10，1，2，|1，4，8，6，3，|11，5，4，7”，B′=“5，7，2，|8，9，6，3，12，|11，12，9，10”。

（3）去重。以 A′为例，先查找交叉区域前面部分与交叉区域中基因相同的基因，可以看到基因1有重复，这时，找到交叉区域中基因1在A中的等位基因8，用它替换交叉区域前的重复基因1。得到：A′=“10，8，2，|1，4，8，6，3，|11，5，4，7”，然后，查找交叉区域后面部分与交叉区域相同的基因，可以发现基因4有重复，这时，找到交叉区域中基因4在A中的等位基因9，用这个基因替换交叉区域后的重复基因 4，得到：A′=“10，8，2，|1，4，8，6，3，|11，5，9，7”。接着，检查 A′的交叉区域与 A 中交叉区域有相同的基因8、6、3，记 C=“8，6，3”，这几个重复基因8、6、3在 A 中对应的等位基因为6、3、12，记D=“6，3，12”，然后去除C 与 D中的重复基因6和3得到C=“8”，D=“12”。接着把 A′中交叉区域前后含有C的那些基因替换为C在D中的等位基因。该例中，可以看到A′交叉区域前面部分含有C中的基因“8”，把其改为 D中的基因“12”，而 A′交叉区域后面部分不含有C 中基因。因此，最后可以得到 A′=“10，12，2，|1，4，8，6，3，|11，5，9，7”。对于B'用相同的方法替换重复基因，最后得到两个新的个体为：A′=“10，12，2，|1，4，8，6，3，|11，5，9，7”，B′=“5，7，2，|8，9，6，3，12，|11，1，4，10”。

4.6 变异操作

变异概率设置为 Pm ，以个体 A=“10，1，2，8，9，6，3，12，11，5，4，7”为例，当该个体发生变异时，随机选择一个变异片段，假设为 A=“10，1，2，|8，9，6，3，12，|11，5，4，7”，其中两个“|”之间部分为即将变异的片段。翻转这个片段得到变异后的个体 A′=“10，1，2，|12，3，6，9，8，|11，5，4，7”。

4.7 重插入操作

为了保证遗传算法能够收敛，把父代中最优的10%的个体直接插入到新产生的下一代中。

4.8 使用LK算法对各代最优个体后优化

使用以上所给的遗传算法，对一个含有25个需求点的订单进行了多次实验，发现即使群体规模设为500，迭代100次以后，在一些最优个体所表示的解中拣选路线仍存在不必要的折回往返情况，种群规模设为500，迭代200次后才基本可以收敛到已知最优解。为了避免这种情况发生，进一步优化解的质量，引入了LK（Lin_Kernighan）算法对各代的最优个体进行后优化。LK算法是S.Lin和B.W.Kernighan于1973年在文献[9]中最早提出的，它是在r-opt算法上发展来的，是求解TSP问题的非常有效的启发式算法，原始的LK算法在求解50个城市的TSP问题时，只需一次计算几乎就能100%地找到最优解[10]，而改进的LK算法[10-11]通过相应的策略来构造替换边集以减少路径判断和交换次数，进而可以以更高的效率求解顶点数过万的大规模的TSP问题。由于一个拣选订单所涉及的需求点一般不会很多，分解成多个拣选作业后，每一条哈密尔顿回路所涉及的需求点更少，因此，本文使用基本的LK算法对各代的最优个体中的多个拣选作业（即多个哈密尔顿回路）进行优化，而后重新计算该个体的适应度值，并把其复制到下一代中，以此来提高解的质量，把本文的这种算法命名为GA-LK算法。之所以仅仅对各代的最优个体进行后优化是考虑到算法的运行时间问题，是在解的质量和运行效率之间的折衷。

4.9 实验参数的选择

根据经验值，一般交叉概率Pc的取值在0.4~0.99，变异概率Pm的取值在0.000 1~0.1[8]。选取交叉概率Pc和变异概率Pm的3个组合进行测试，分别为Pc=0.6，Pm=0.05；Pc=0.8，Pm=0.1；Pc=0.9，Pm=0.1；之所以选择较大的变异概率是因为考虑到路径优化的特殊性以及本文中染色体变异的特定操作是反转特定的染色体片段，而根据以前的实验，发现有些路径存在往复等情况，反转染色体片段会在一定程度上解决此问题。每个组合对于特定的种群规模和迭代次数进行了3次实验，实验结果见表1所示。

表1 参数选择对比

从以上实验结果可以看出，当设置较大的初始种群和迭代次数时参数选择Pc=0.6，Pm=0.05所获得的平均拣选路径较短，也即可以以较大的概率获得更好的解。而当设置较小的初始种群和迭代次数时，参数选择Pc=0.8，Pm=0.1可以以较大的概率获得更好的解。由于希望算法执行的更快些，因此，本文最终选择Pc=0.8，Pm=0.1。

5 实验评测

在这一部分，就第4部分提出的GA-LK算法与粒子群优化算法[12]以及遗传粒子群算法[13-15]进行了对比。为了具有可比性，将粒子群算法及遗传粒子群算法每代的最优个体也进行了后优化，也即使用LK算法对其进行了优化。

5.1 实验设计

随机产生一个含有25个需求点的订单（见图4中标记的25个需求点），25个货位编号分别为：186、98、116、48、217、52、54、26、141、143、47、222、36、225、37、31、138、220、65、234、126、30、45、169、5，各个货位的需求量为 16、19、17、18、11、18、2、2、14 、3、13、20、6、11、6、7、13、17、4、8、4、9、10、15、3，拣选设备容量限制为100，该订单已知的最优拣选路径长度为184。

5.2 各算法实验结果的比较

对于设定的某一群体规模和迭代次数随机进行8次重复实验，实验结果见表2所示。

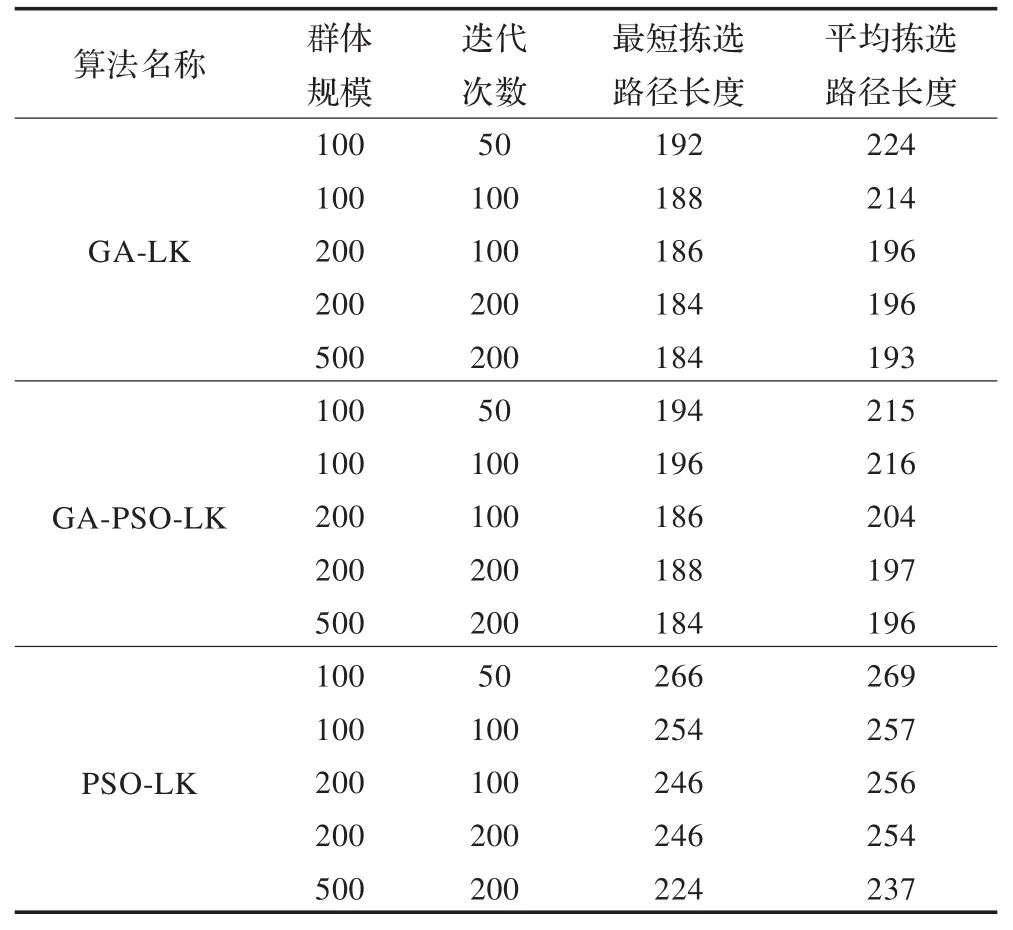
表2 各算法实验结果

表2中，PSO-LK为粒子群LK算法，即在粒子群算法的每次迭代后，用LK算法优化每代的最优解；GA-PSO-LK为遗传粒子群LK算法。PSO-LK算法中的粒子速度更新公式为（15），位置更新公式为（16）：

其中，v是粒子的速度，persent是粒子的当前位置，pbest是该粒子所经历过的最好位置，gbest是整个种群当前获得的最好位置，rand是介于0、1之间的随机数。实验中学习因子c1、c2设置为2，较大的惯性因子w适于对解空间进行大范围探查，较小的w适于进行小范围开挖。实验中w设置为随迭代次数的增加而逐渐变小：w=0.9-0.7×gn/gnmax，其中gn为当前代数，gnmax为设置的迭代次数。

GA-PSO-LK算法是对GA-LK算法在交叉阶段进行了修改，在每一代的交叉阶段以交叉概率1进行交叉，不是两两随机配对进行交叉操作，而是将该个体与历史上全局最优个体进行交叉，然后再与该个体所经历的最好个体进行交叉以期望获得更好的后代，而后根据变异概率Pm=0.1进行变异，然后再用LK算法对每代的最优解再次优化。

从表2可以看出，对于GA-LK算法，当实验群体规模设置为200，迭代次数为100时，实验8次得到的平均解与已知的最优解相差不过7%，可基本收敛到已知的最优解，图6是这8次实验中最成功的1次实验所获得的最优解的进化情况，从图6可以看到，初始随机产生200个个体中最好的拣选路线长度大概为360，经过100次迭代后最优拣选路径长度为186，节省了近一半的拣选长度，说明算法应用于实际订单拣选时将是有效的。图7是这次实验所获得的最优个体所表示的拣选路径，从图7可以看出该订单需要分解为三次拣选作业，图7中需求点旁边所注的编号为这个需求点在这个拣选作业中的作业次序号，用以引导操作人员进行拣选作业，对于一个大的订单，分解成较多拣选作业的情况，可以依次将每个拣选作业的路径绘制在移动终端上，当作业人员完成了本次拣选作业后再绘制下一个作业的拣选路径，或者将该订单的多个拣选作业路径分别绘制在多个拣选作业人员的移动终端上以引导多个作业人员同时对一个订单进行拣选。从图7可以看出最优拣选路径中的各拣选作业不存在多余的折回往返情况。

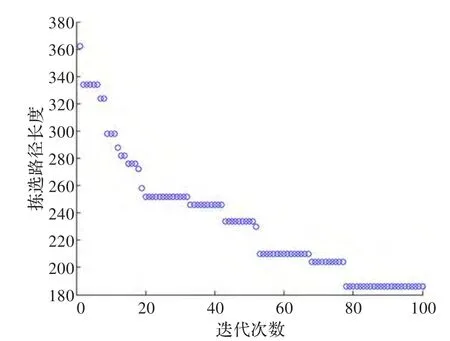
图6 最优解进化情况

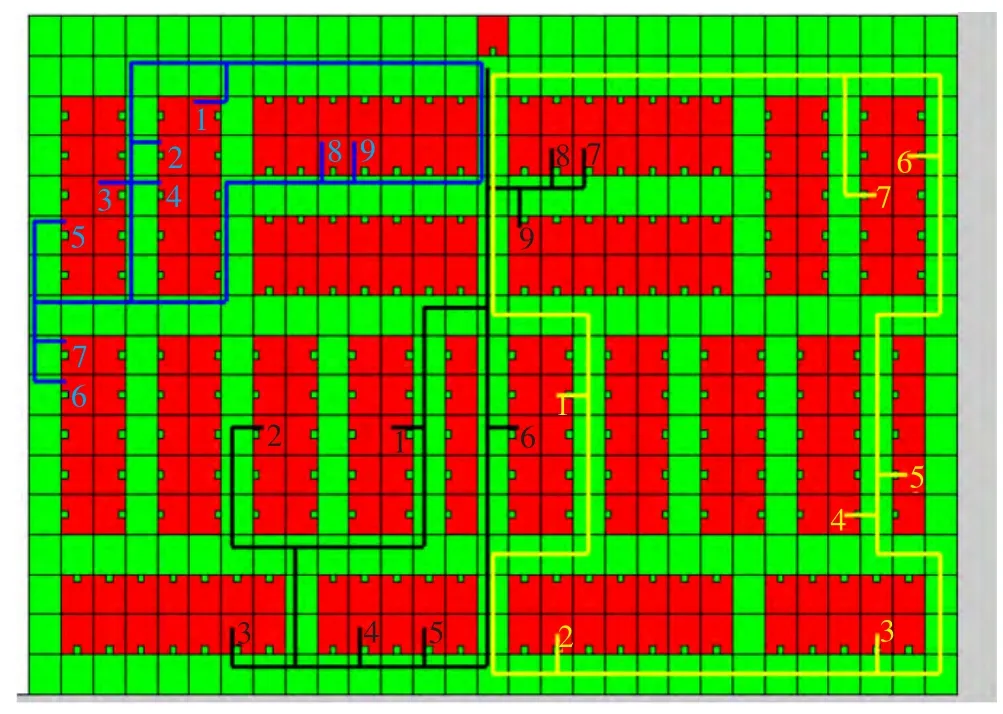
图7 订单最优拣选路径

表2的实验结果表明，PSO-LK算法表现出过早收敛，随着种群规模扩大及迭代次数增加解的质量改进不大，解的质量普遍差于GA-LK算法。而GA-PSO-LK算法获得的解的质量稍差于GA-LK算法。这两种粒子群算法都不如GA-LK算法，可能是因为问题的维数较大，粒子在高维空间中的移动仅仅共享了全局最优位置，而相互之间没有交换更多的信息。PSO-LK算法是让粒子向着种群当前最优解位置以及该粒子所经历的最好位置的夹角中某一方向移动，而更好的位置并非一定位于这一夹角之中，而GA-PSO-LK算法中借鉴了GA算法的交叉操作使得新的位置可以跳出这一夹角，扩大了搜索的范围导致解的质量较好。

拣选设备的容量限制主要有两个维度，一个是容积，一个是载重量。而拣选作业既要满足拣选设备容积限制又要满足载重量限制，在计算订单的最大拣选次数K时，分别从容积和载重量这两个方面来计算，而后取较大的那个数再乘以一个大于1的经验系数作为最大拣选次数。在计算一个染色体的函数值时是该染色体对应的路径长度加上这两个维度上的惩罚值作为该染色体的函数值，依据此函数值计算该染色体的适应度值。在大多数实际应用中，根据实际问题的特点，只需关注某一维度的限制即可，例如对于载重量大的拣选设备只需关注它的容积限制，对于体积小而较重的物品只需关注拣选设备的载重量限制。

6 结论

订单拣选是物流业中最为频繁的作业之一，并非所有的行业都适合采用自动化立体仓库，对于需要在横竖不一的各巷道间移动拣选的情况，本文给出了一种解决方法，实验结果表明此方法是可行有效的，它可以对超市、书店等场合的配货和补货作业进行路径优化。

容量限制的订单拣选问题属于CVRP（Capacitated Vehicle Routing Problem）问题，对于大规模的CVRP问题，遗传算法的初始群体需要更好的设计，另外在迭代中尽量避免产生不符合约束的解，并且迭代中产生的符合约束条件的解尽量分散于解空间中以避免过早收敛，但这也会增加算法的时间复杂度和空间复杂度。对于更大规模的CVRP问题需要设计更高效的启发式算法，在求解结果与所花费时间代价之间进行折衷，这也是下一步的努力方向。

[1]刘臣奇，李梅娟，陈雪波.基于蚁群算法的拣选作业优化问题[J].系统工程理论与实践，2009（3）：179-184.

[2]常发亮，刘增晓.自动化立体仓库拣选作业路径优化问题研究[J].系统工程理论与实践，2007（2）：139-143.

[3]李梅娟，陈雪波，王莉.多巷道固定货架拣选作业优化问题的研究[J].控制与决策，2008（12）：1338-1342.

[4]Filipec M，Skrlec D，Slavko K.An efficient implementation of genetic algorithms for constrained vehicle routing problem[C]//Proceedings of IEEE International Conference on System，Man and Cybernetics，1998.

[5]胡运权，郭耀煌.运筹学教程[M].3版.北京：清华大学出版社，2007.

[6]Holland J H.Adaptation and artificial systems[M].Ann Arbor：University of Michigan Press，1975.

[7]徐洪泽，陈桂林，张福恩.遗传算法的单双点杂交方法对比研究[J].哈尔滨工业大学学报，1998（4）：64-71.

[8]雷英杰.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005.

[9]Lin S，Kernighan B W.An efficient heuristic algorithm for the traveling salesman problem[J].Operations Research，1973，21：498-516.

[10]Helsgaun K.An effective implementation of the Lin-Kernighan traveling salesman heuristic[J].European Journal of Operational Research，2000，126：106-130.

[11]Walshaw C.A multilevel lin-kernighan-helsgaun algorithm for the travelling salesman problem[R]//Mathematics Research Report，2001-09-27.

[12]李爱国，覃征.粒子群优化算法[J].计算机工程与应用，2002，38（2）：1-3.

[13]吕振肃，侯志荣.自适应变异的粒子群优化算法[J].电子学报，2004（3）：416-420.

[14]高尚，韩斌.求解旅行商问题的混合粒子群优化算法[J].控制与决策，2004（11）：1286-1289.

[15]刘衍民，牛奔，赵庆祯.基于交叉和变异的多目标粒子群算法[J].计算机应用，2011（1）：82-84.