ZY环

周 颖，李德才，魏俊潮＊

（1．扬州大学数学科学学院，江苏 扬州225002；2．扬州职业大学，江苏 扬州225009）

本文中R 表示有单位元的结合环，E（R），N（R），Z（R）分别表示R 的幂等元集合、幂零元集合及R 的中心．设R 为一个环，若对任意a∈R，存在b∈R，使得a＝aba，则称R 为von Neumann正则环［1］；若对任意a∈R，存在b∈R，使得a＝ba2，则称R 为强正则环［2］；若N（R）⊆Z（R），则称R 为CN环［3］．显然，交换环、约化环都是CN 环；关于CN 环的研究可参见文献［4－5］．若E（R）⊆Z（R），则称R 为Abel环．显然CN 环是Abel环．若对a，b∈R，当ab＝1时，必有ba＝1，则称R 为直接有限环［6］．易知Abel环是直接有限环；若N（R）＝0，则称R 为约化环［7］；若对任意a∈R，当aRa＝0时必有a＝0，则称R 为半素环．显然约化环是半素环．若ab＝0时必有aRb⊆N（R），则称R 为nil－semicommutative环［8－9］．

设R 是一个环，若对任意x∈N（R），y∈R，总有x2y2＝xy2x，则称R 为ZY 环．易见CN 环总是ZY 环，从而交换环及约化环是ZY 环．但反过来不一定成立．例如：设易见，则有A2B2＝AB2A＝0，所以R 为ZY 环．取，由于所以CD≠DC，C∉Z（R），从而N（R）⊄Z（R），R 不是CN 环，因此R 既不是交换环也不是约化环．本文研究ZY环的一些性质，推广有关约化环及CN 环的若干结果．

命题1设R 为CN 环，则是ZY 环．

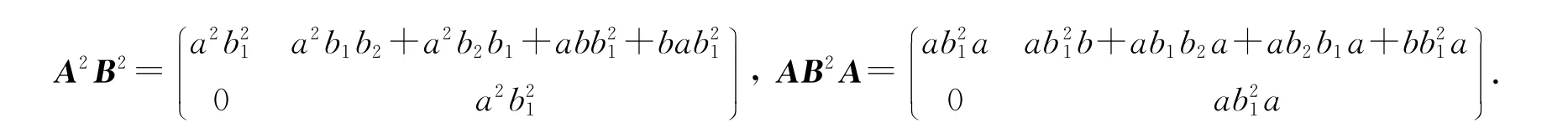
因为a∈Z（R），所以ab21a＝a2b21；又由于b1a∈N（R）⊆Z（R），所以ab2（b1a）＝b1aab2＝b1a2b2＝a2b1b2．同理可证ab21b＝abb21，ab1b2a＝a2b2b1，bb21a＝bab21，从而A2B2＝AB2A，因此V2（R）为ZY 环．

定理2设R 是ZY 环且a∈R，若a2＝0，则aRaRa＝0．

证明 因为R 为ZY 环且a2＝0，所以对任意x∈R，总有

任取y∈R，用x＋ya代替（1）式中的x，得ayaxa＝0，由x，y 的任意性知aRaRa＝0．

由定理2可知有下面的推论．

推论3R 为约化环当且仅当R 为ZY 的半素环．

定理4设R 为ZY 环且a∈aRa，则存在c∈R，使得a＝ca2．

证明 设a＝aba，其中b∈R．记e＝ba，则有a＝ae且e2＝e；记h＝a－ea，则有he＝h，eh＝0，h2＝0，即h∈N（R）．因为R 为ZY 环，所以对任意x∈R，有

用x＋b代替（2）式中的x，得hbxh＋hxbh＝0，特别取x＝e，则有hbh＝0．因为bh＝b（a－ea）＝babea＝e－bea，所以0＝hbh＝h（e－bea）＝h－hbea，从而h＝hbea，即a－ea＝hbea，因此a＝ea＋hbea＝（1＋hb）ea＝（1＋hb）ba2．若取c＝（1＋hb）b∈R，则a＝ca2．

众所周知，一个环R 是强正则环当且仅当R 为约化的正则环，所以推论3和定理4暗示了下面的推论．

推论5R 为强正则环当且仅当R 为ZY 的正则环．

推论6设R 为ZY 环，则R 为直接有限环．

证明 设a，b∈R，满足ab＝1，则a＝1a＝aba．由定理4知存在c∈R，使得a＝ca2，于是1＝ab＝ca2b＝（ca）（ab）＝（ca）1＝ca，因此b＝1b＝（ca）b＝c（ab）＝c，ba＝ca＝1，从而R 为直接有限环．

定理7设R 为ZY 环，则对任意的e∈E（R），a∈R，有（1－e）aeR（1－e）ae＝0．

证明 记h＝（1－e）ae，则he＝h，eh＝0，所以h2＝heh＝0．类似于定理4的证明知hRh＝0，从而（1－e）aeR（1－e）ae＝0．

设R 是一个环，如果N（R）＝0，或者N（R）包含一个非零理想，则称R 为NCI环［10］．例如，CN 环是NCI环．

推论8设R 是ZY 环，则R 为Abel环或为NCI环．

证明 如果R 不是Abel环，则存在e∈E（R），使得eR（1－e）≠0，从而存在a∈R，使得ea（1－e）≠0．由于设R 是ZY 环，所以由定理7知ea（1－e）Rea（1－e）＝0，从而Rea（1－e）R 是包含在N（R）中的非零理想，因此R 为NCI环．

定理9设R 为ZY 环且e∈E（R），则对R 的任意极大左理想M，或者e∈M 或者1－e∈M．

证明 若e∉M，则Re＋M＝R．记1＝ae＋m，其中a∈R，m∈M．由于1－e＝（1－e）ae＋（1－e）m，由定理7知（1－e）aeR（1－e）aeR＝0，所以（1－e）aeR 为幂零右理想，从而（1－e）ae∈J（R）⊆M，因此1－e∈M．

推论10设R 为ZY 环，则对任意e∈E（R）及R 的任意极大左理想M，有Me⊆M．

证明 若Me⊄M，则M＋Me＝R，所以有n＋me＝1，其中n，m∈M．因为e∉M，由定理9知1－e∈M，故有m（1－e）∈M；又因m∈M，故me∈M．由于n＋me∈M，所以1∈M，矛盾，从而Me⊆M．

推论11设R 为ZY 环，则对任意的x∈R，e∈E（R），有Rx＋R（xe－1）＝R．

证明 若Rx＋R（xe－1）≠R，则有R 的极大左理想M，使得Rx＋R（xe－1）⊆M．因为xe－1∈M，而1∉M，所以xe∉M，即e∉M．由定理9知1－e∈M，故x－xe＝x（1－e）∈M．由于x∈M，所以xe∈M，矛盾，因此Rx＋R（xe－1）＝R．

定理12若R 为一个环，满足对任意x∈N（R），y∈R，总有（xy）2＝xy2x，则R 为ZY 环．

证明 任取a∈N（R），x∈R，由题设有（ax）2＝ax2a，从而

用1＋x 代替（3）式中的x，得

由（3）和（4）式知a［a，x］＝0，即

用x2代替（5）式中的x，则a2x2＝ax2a，所以R 为ZY 环．

定理13ZY 环为nil－semicommutative环．

证明 设R 为ZY 环且a，b∈R 满足ab＝0．由于（ba）2＝0，所以对任意x∈R，有

任取y∈R，用x＋ya代替（6）式中的x，得bayaxba＝0，所以baRaRba＝0；于是对任意的r∈R，有（bar）3＝ba（rb）arbar＝0，（arb）4＝ar（bar）3b＝0，即aRb⊆N（R），故R 为nil－semicommutative环．

注14Nil－semicommutative环未必是ZY 环．例如：设取A＝则 有所 以A2B2≠AB2A，即R 不是ZY 环．设，则cidi＝0，i＝1，4，6．对任意的由于Z2为交换环，故cixidi＝0，i＝1，4，6，从而则有（CFD）3＝0，即CFD∈N（R），于是CRD⊆N（R），因此R 为nil－semi－commutative环．

定理15设R 为ZY 环且e∈E（R），若ReR＝R，则e＝1．

证明 由于ReR＝R，所以1＝∑aiebi，ai，bi∈R．由定理7知（1－e）aieR（1－e）aie＝0，所以（1－e）aie∈J（R），从而1－e＝（1－e）·1＝∑n

i＝1（1－e）aiebi∈J（R），因此1＝e．

［1］ WANG L，WEI J C．Central semicommutative rings［J］．Indian J Pure Appl Math，2014，45（1）：13－25．

［2］ WANG Long，WEI Junchao．Weakly semicommutative rings and strongly regular rings［J］．Kyungpook Math J，2014，54（1）：65－72．

［3］ BURCU U，SAIT H，HANDAN K，et al．Rings in which every nilpotent is central［J］．Algebras Groups Geom，2013，30（1）：1－18．

［4］ 熊丽丽，李男杰，魏俊潮．CN－环［J］．扬州大学学报：自然科学版，2011，14（2）：7－9．

［5］ WEI Junchao．Some notes on CN rings［J］．Bull Malays Math Sci Soc，2014，37（3）：25－37．

［6］ NICHOLSON W K，YOUSIFF M F．On a theorem of Camillo［J］．Commun Algebra，1995，23（14）：5309－5314．

［7］ REGE M B．On von Neumann regular rings and SF－rings［J］．Math Japon，1986，31（6）：927－936．

［8］ CHEN Weixing．On nil－semicommutative rings［J］．Thai J Math，2011，9（1）：39－47．

［9］ QU Yinchun，WEI Junchao．Some notes on nil－semicommutative rings［J］．Turk J Math，2014，38（2）：212－224．

［10］ HWANG S U，JEON Y C，PARK K S．On NCI rings［J］．Bull Korean Math Soc，2007，44（2）：215－224．