多尺度有限元法在Shishkin边界层的数值模拟

孙美玲，江 山，唐元生

（1．扬州大学数学科学学院，江苏 扬州225002；2．南通职业大学教育技术中心，江苏 南通226007）

奇异摄动问题广泛存在于弹性力学、流体力学、分子动力学等领域，其微分方程中含有摄动系数ε，系数很小时将导致原问题失去边界条件，在所谓的边界层区域出现跳跃或剧烈变化．面对现实中大量的跨尺度问题无法进行有效求解，因此研究奇异摄动的高效数值模拟有重要的现实意义［1－3］．处理奇异摄动边界层现象主要采取两种方式：一是非一致网格或分层网格的h－方式（h 是网格变步长）［4－6］；二是定义单元逼近多项式的p－方式（p 是多项式的次数）或hp－方式（二者的结合）［7－9］．例如，Stynes和O’Riordan［4］利用Galerkin有限元法在Shishkin网格上处理二维对流扩散方程，得到了一致收敛的全局能量范数解．如今，越来越多的多尺度问题出现在科学和工程计算中，如复合材料的性态功能、多孔介质的流相分析、湍流现象、集成电路设计等．面对大规模、高精度计算的实际需求，人们一直致力于寻求既能保证计算精度，又可节约计算资源的新数值方法来处理复杂的多尺度问题，从而推动多尺度计算的发展［10－14］．多尺度有限元法（multiscale finite element method，简记为MsFEM）就是其中一个重要分支［10］．

本文考虑奇异摄动的二维反应扩散偏微分方程

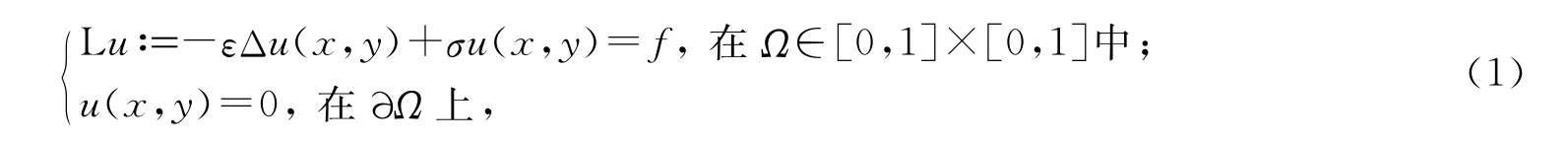
其中L是含参数ε，σ的微分算子，ε≪1为摄动系数，当其很小时会出现边界层现象，传统数值方法将失去精度和稳定性；u是真解，f 是右端函数，Ω 为二维区域及其边界∂Ω．该问题的精确、高效数值解是本文的求解目标，以期得到不依赖于ε参数大小的一致收敛．

1 多尺度有限元与边界层的Shishkin网格

1．1 变分形式与多尺度有限元法

问题（1）的变分形式是寻求u∈H10，满足

构造标准有限元的泛函空间Vh＝｛vh∈H1（Ω）：vh｜K∈Q1（K）｝，其中Q1（K）表示单元K 上的双线性函数，且令Vh0＝Vh∩H10（Ω）．采用传统的Galerkin有限元法，对应的变分形式是寻求ug∈Vh0，满足

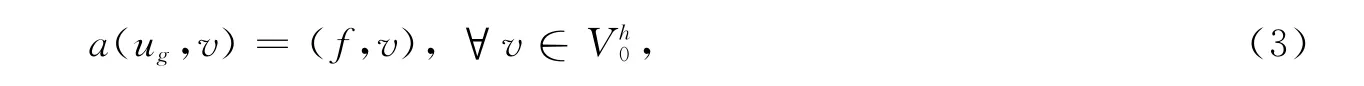
其中ug是Galerkin有限元解．

将二维区域Ω 分解为不重叠的分块Ωi且∪Ωi＝Ω，令Κh是Ω 的矩形网格剖分，故在每一个粗单元K∈Κh上定义4个节点的离散基函数．采用新的多尺度有限元法，对应的变分形式是寻求uh∈Uh，满足

其中uh就是多尺度有限元解，而多尺度泛函空间Uh是由多尺度基函数所张成的．

1．2 多尺度基函数的子问题

在粗网格单元K 上求解对应的多尺度基函数子问题

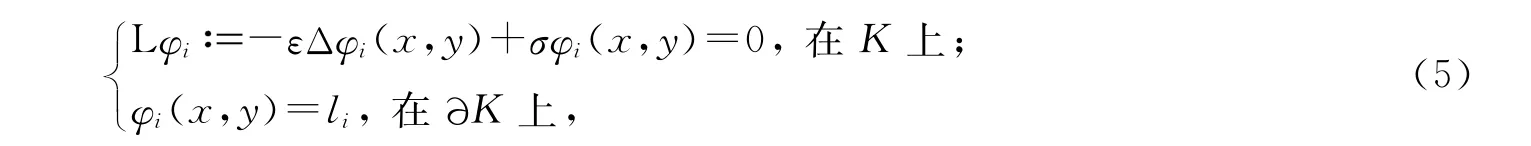
给定该边值子问题的线性边界条件li，即当i＝j时φi（xj，yj）＝1；当i≠j时φi（xj，yj）＝0；且在边界∂K 上呈现线性变化．因为子问题（5）与原问题（1）都有微分算子L，故可通过求解（5）获得多尺度基函数φi 的数值解，从而获得粗网格单元K 上的微观信息．

需要说明的是，只有当单元K 是边界层上的单元时，才求解子问题（5）以获得多尺度基函数φi，这样φi 可以很好地反映刻画出原问题（1）在粗网格上的局部信息，如奇异摄动性，构造多尺度空间Uh＝span｛φi：i＝1，…，4，∀K∈Κh｝．而在非边界层的光滑单元，仍然用传统有限元基函数ψi 所张成的函数空间Vh＝span｛ψi：i＝1，…，4，∀K∈Κh｝．这样，将奇异摄动的边界层局部性态引入到多尺度基函数，通过多尺度有限元格式的总刚度矩阵组装并求解，在宏观粗网格上即可用较少的计算资源获得精度更高的数值结果uh．

1．3 Shishkin网格

对于奇异摄动问题，只有当摄动系数ε很小时才出现边界层现象．若对模型问题进行先验分析知其边界层出现于何处，则可对该边界层区域采取特定的非一致网格剖分．这样，在网格剖分总量不变的前提下，某些网格加密能更好地逼近边界层，而某些网格变粗足以逼近解的光滑部分，此即为h－方式下Shishkin网格的思想，从而形成分片等距网格剖分．

选定参数ε，取x，y 方向的粗网格剖分数N，则过渡点τ两侧都以N／2个粗单元进行剖分．二维离散节点坐标（xi，yj）定义为

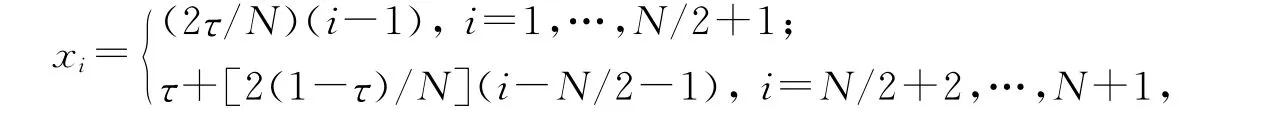
类似可得yj．对于二维问题边界层，取，则子区域上采用较密网格剖分，而上采用较疏网格剖分，从而形成多尺度有限元求解的粗网格分块．

2 数值实验

针对二维反应扩散偏微分方程，取单个方向x，y 等距剖分数为N，在二维网格O（N2）上求解离散数值结果．本文分别采用传统有限元法（FEM）和多尺度有限元法（MsFEM）计算数值算例，随着剖分数N 的增加，比较两种数值方法在精度和稳定性方面的优劣．

在L2范数和H1范数意义下，数值解的误差定义为

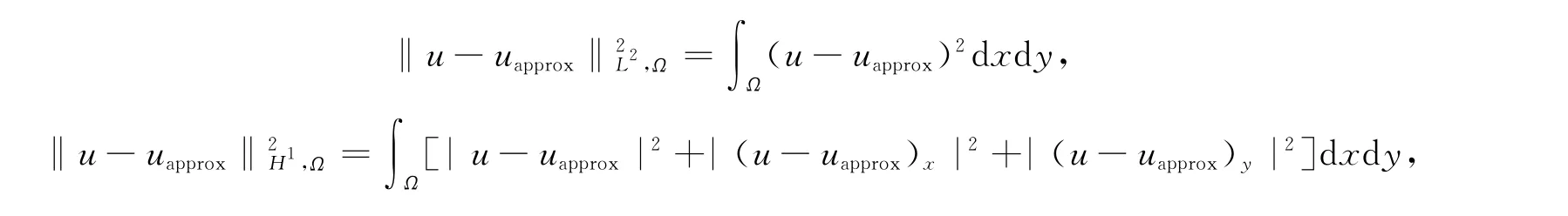
其中u表示真解，uapprox表示不同方法对应的数值解，其值大小作为度量数值方法优劣的依据．

算例设问题（1）的真解u（x，y）＝（x－1）（y－1）（e－x／ε－1）（e－y／ε－1），可知边界层在x，y 轴附近，选定ε与σ＝2并构造出对应的右端f．

可以知道，当ε较大时不会出现奇异摄动的边界层现象，传统数值方法已能有效处理原问题，相应的数值计算结果这里不列出．但当ε很小时，解在边界层出现跳跃现象，为便于比较，用传统有限元法和多尺度有限元法分别求解相关范数．从表1可以看出，当ε＝10－4时，FEM 的精度很差，加密网格剖分反而出现发散的负阶收敛率．与其相比，MsFEM 的结果精度好得多，而且随着网格剖分的加密，呈现出2阶收敛的L2范数与1阶收敛的H1范数，充分验证了多尺度有限元数值解的精确度和稳定性．

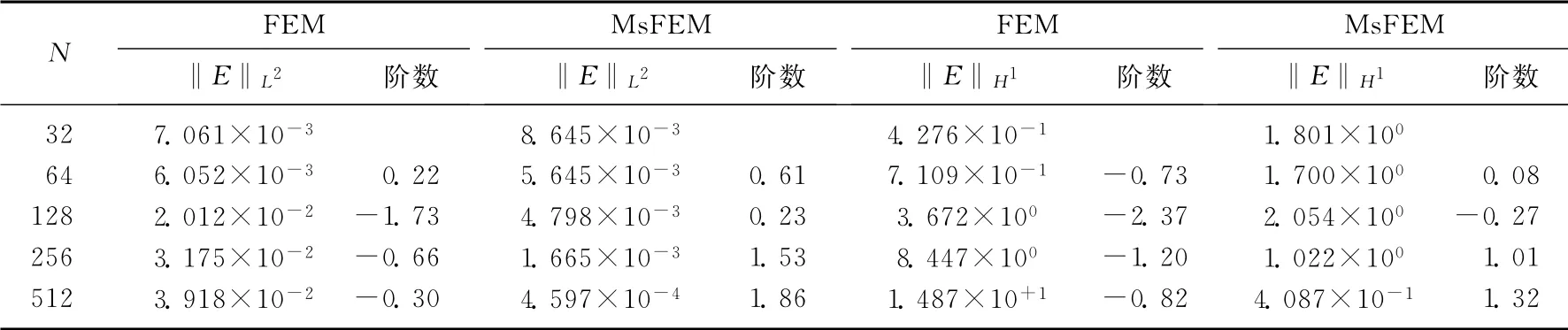
表1 当ε＝10－4时，传统有限元法与多尺度有限元法在Shishkin网格上求解算例得到的L2 范数和H1 范数Tab．1 Whenε＝10－4，L2 and H1 norms obtained by using the FEM and the MsFEM on Shishkin grid

由图1可以看出，当ε＝10－4（很小）时，真解u［图1（b）］在x，y 轴附近才出现边界层现象，解发生急剧跳跃．观察图2可见，当ε＝10－4、剖分数N＝256时，传统有限元法误差依然很大［图2（a）］，如z轴上限达到0．8；而多尺度有限元法的误差［图2（b）］，取Shishkin网格过渡点z轴的上限仅为0．2，而且边界层的误差无论大小还是宽幅都比前者要小许多，这归功于多尺度基函数在Shishkin网格上获得了有效的局部逼近信息．

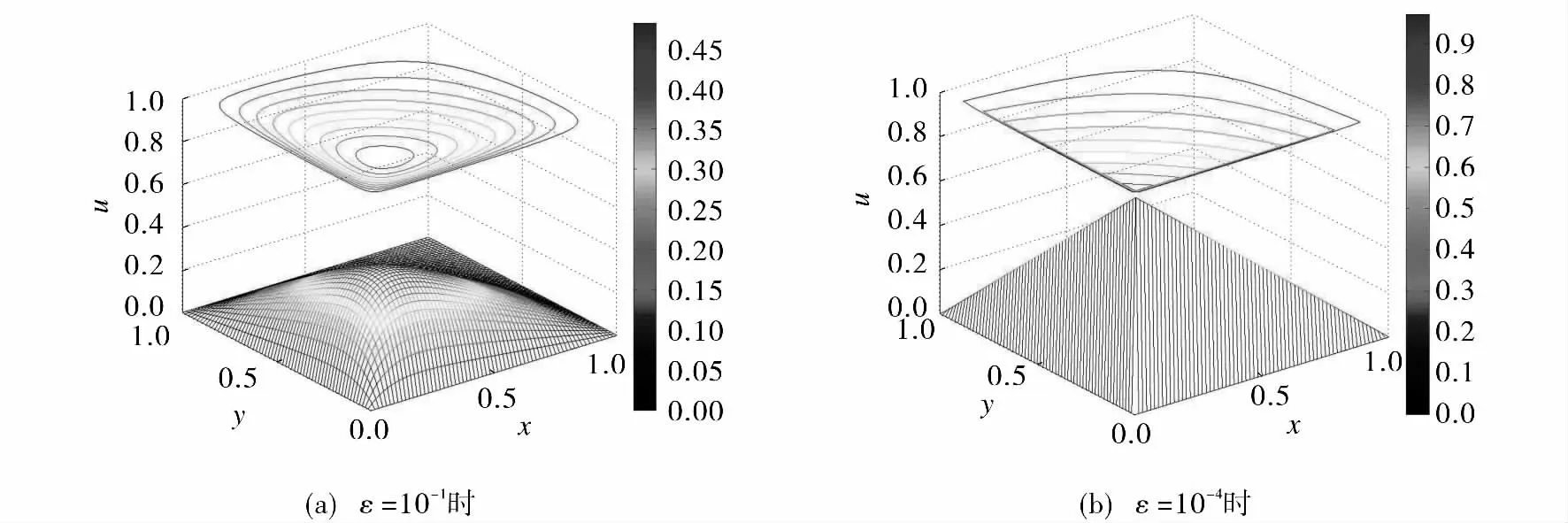
图1 ε分别取10－1，10－4时的真解Fig．1 The exact solutions whenε＝10－1 and 10－4

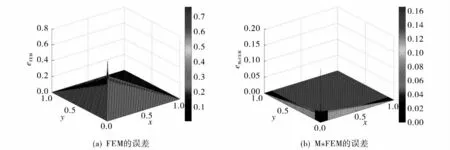
图2 当ε＝10－4，N＝256时，传统有限元法（a）和多尺度有限元法（b）在Shishkin网格上获得的误差图Fig．2 Whenε＝10－4，N＝256，the error figures shown by the traditional FEM （a）and the MsFEM on Shishkin grid（b）