一类含有位势的快扩散方程组的Fujita指标

史金鑫，沈娟娟

（南通大学理学院，江苏 南通226007）

在偏微分方程中，关于Fujita指标的研究已引起许多学者的关注．1993年，Qi等人［1］研究了问题ut＝Δum＋vp，vt＝Δvn＋uq，得到（pq）c＝mn＋2 N－1max｛p＋n，q＋m｝．2013年，Yang等人［2］研究了齐次快扩散方程组ut＝Δum＋vp＋f1（x），vt＝Δvn＋uq＋f2（x），其中0＜m，n＜1，得到Fujita指标为（pq）c＝mn＋2（N－2）－1max｛mp＋mn，nq＋mn｝．崔世泽等人［3］探究了耦合方程组ut＝vpΔu，vt＝uqΔv在有界区域上解的整体存在性和爆破．

近年来，带有衰减位势的热方程的渐近行为又引起人们的广泛关注．Zhang［4］通过研究柯西问题

说明了位势对Fujita指标的影响，但当位势以平方速度衰减时没有得到问题（1）的Fujita指标．而Ishige［5］和Pinsky［6］的研究证明了当位势以平方速度衰减时，问题（1）的Fujita指标为pc（n，ω）＝1＋2／［α（ω）＋N］，其中N 表示空间维数，α（ω）＞0，满足α（α＋N－2）＝ω．关于位势问题还可参见文献［7－9］．最近，Yang等人［10］研究了带有平方速度衰减的位势的快扩散方程ut＝Δum－V（x）um＋up，得到pc（N，m，ω）＝m＋2／［mα（ω，m）＋N］，其中α（ω，m）＞0，满足mα（mα＋N－2）＝ω．受以上工作的启发，本文拟将文献［10］中的结果推广到方程组的情形，探讨当位势以平方速度衰减时对Fujita指标的影响．

1 主要结果

在RN中考虑如下含有位势的初值问题的Fujita指标：

其中1－2／（mα1＋N）＜m＜1，1－2／（nα2＋N）＜n＜1，p，q＞1，pq＞1，N≥2，位势φ（x）～ω1／｜x｜2，ψ（x）～ω2／｜x｜2，且当｜x｜→∞时ω1，ω2≥0为常数，α1，α2＞0是与ω1，ω2有关的参数，并满足mα1（mα1＋N－2）－ω1＝0，nα2（nα2＋N－2）－ω2＝0，α1（1－m）＝α2（1－n），u0，v0是连续有界的．

记pc＝［2＋m（mα1＋N）］／（N＋nα2），qc＝［2＋n（nα2＋N）］／（N＋mα1）．本文的主要结论如下．

定理1假设1＜p≤pc，1＜q≤qc，V1（x），V2（x）∈Cγ（RN＼｛0｝），γ∈（0，1），对充分大的｜x｜，有V1（x）≤ω1／｜x｜2，V2（x）≤ω2／｜x｜2，则问题（2）的非负解在有限时间内爆破．

定理2假设p＞pc，q＞qc，V1（x），V2（x）∈Cγ（RN＼｛0｝），γ∈（0，1），V1（x）≥ω1／｜x｜2，V2（x）≥ω2／｜x｜2，则问题（2）存在全局解．

2 定理的证明

2．1 定理1的证明

笔者利用试验函数法证明问题（2）的解在有限时间内爆破．

假设U（r，t）＝rα1ω（r，t），V（r，t）＝rα2z（r，t）是问题（2）的下解，且0≤U0（r）≤u0（x），U0′（r）≤0，0≤V0（r）≤v0（x），V0′（r）≤0，则对充分大的r0，当r＞r0，t∈（0，T），ω（r，0）＝r－α1U0（r）≥0，z（r，0）＝r－α2V0（r）≥0时，ω，z满足

设ρ＝ρ（r）＝2r［α1（1－m）＋2］／2／［α1（1－m）＋2］，σ＝σ（r）＝2r［α2（1－n）＋2］／2／［α2（1－n）＋2］，ρ0＝ρ（r0），σ0＝σ（r0），记ω（r，t）＝ξ（ρ，t），z（r，t）＝η（σ，t），则当

时，式（3）变为

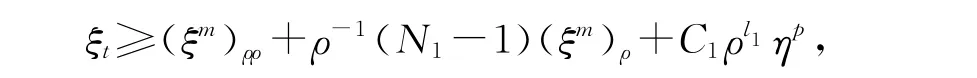
其中N1＝（2α1＋2mα1＋2 N）／［α1（1－m）＋2］，C1＝［2－1α1（1－m）＋1］2（α2p－α1）／［α1（1－m）＋2］，l1＝2（α2p－α1）／［α1（1－m）＋2］．同理，式（4）可变为

其中N2＝（2α2＋2nα2＋2 N）／［α2（1－n）＋2］，C2＝［2－1α2（1－n）＋1］2（α1q－α2）／［α2（1－n）＋2］，l2＝2（α1q－α2）／［α2（1－n）＋2］．取ν，μ 满足

若能证明（ν，μ）在有限时间内爆破，则可知问题（2）的解在有限时间内爆破．假设（ν，μ）为问题（5）的全局解，光 滑 函 数其中x＝ρ（或σ）．定 义

由Hölder不等式得

因为α1（1－m）＝α2（1－n），故

其中

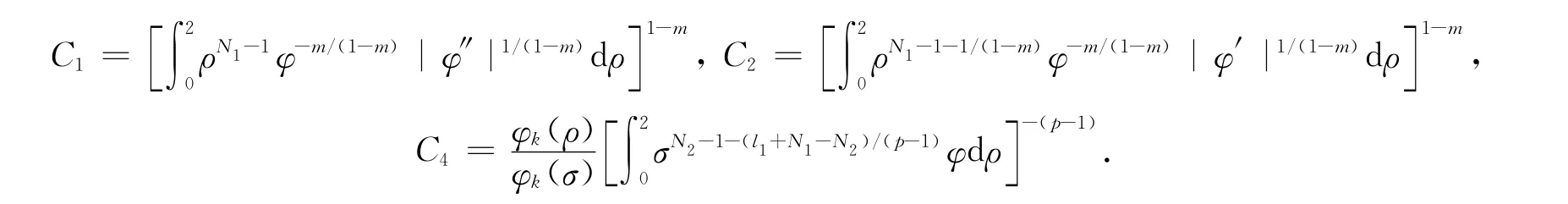
显然C1，C2，C4＜∞，令C3＝C1＋（N1－1）C2，则

同理可得

若p＜pc，q＜qc，则－2＋N1（1－m）＜l1＋N1－N2p，－2＋N2（1－n）＜l2＋N2－N1q．由于pq＞mn，故 存 在σ1，σ2＞0，使 得Fk（0）＞σn／（mn－pq）1σp／（mn－pq）2，Fmk（0）／Gpk（0）＜σ1，Gk（0）＞σq／（mn－pq）1σm／（mn－pq）2，Gnk（0）／Fqk（0）＜σ2．由式（9），（10）知存在C7，C8＞0以及充分大的k0，k＞k0使得Fk′（0）≥C7Gpk（0），Gk′（0）≥C8Fqk（0）．更进一步，由pq＞1得Fk′≥C7Gpk，Gk′≥C8Fqk，因此当1＜p＜pc，1＜q＜qc时，问题（2）的解在有限时间内爆破．

若p＝pc，q＝qc，则－2＋N1（1－m）＝l1＋N1－N2p，－2＋N2（1－n）＝l2＋N2－N1q．由式（9），（10）知存在t0＞0使得

假设对所有的k，t＞0有Fk（t）≤K1，Gk（t）≤K2．因为－2＋N1（1－m）＝l1＋N1－N2p＜0，－2＋N2（1－n）＝l2＋N2－N1q＜0及1－2／（mα1＋N）＜m＜1，1－2／（nα2＋N）＜n＜1，

2．2 定理2的证明

受文献［10］882的启发，构建问题（2）的上解

其中B1，B2，D1，D2＞0，只须证（¯u，¯v）是问题（2）的全局的上解即可．首先验证

设Z1＝B1＋D1r2＋α1（1－m）（t＋1）－1－β1（1－m）＝B1＋D1z1，Z2＝B2＋D2r2＋α1（1－m）（t＋1）－1－β2（1－n）＝B2＋D2z2，则¯ut－（¯um）rr－r－1（N－1）（¯um）r＋r－2ω1¯um－¯vp≥（t＋1）－β1－1rα1Z－1／（1－m）－11F（Z1），其中

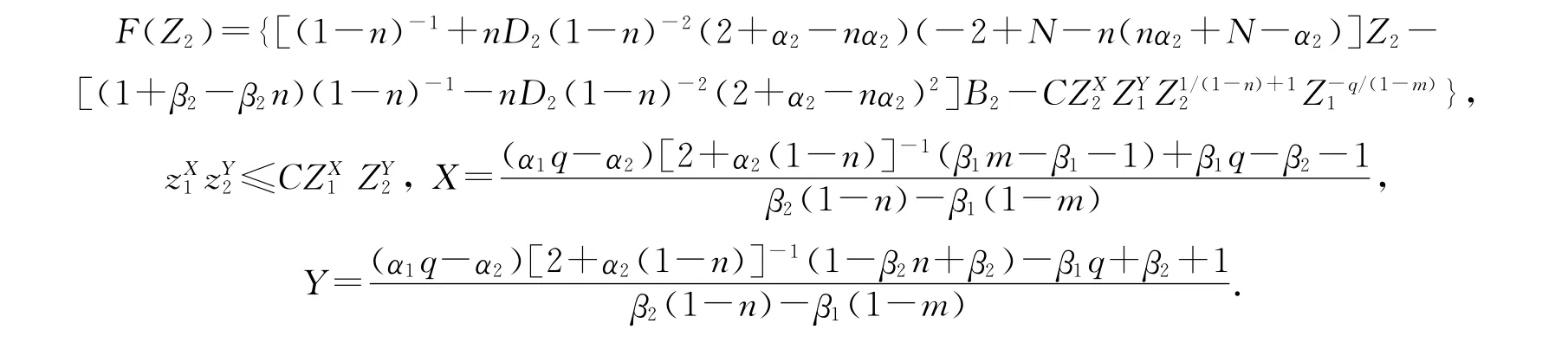
本文总是假设J＋（1－m）－1＜0，X＋（1－n）－1＜0，要证F（Z1）≥0，F（Z2）≥0，只须证（i）F（B1）≥0，F（B2）≥0；（ii）F′（Z1）≥0，Z1≥B1，F′（Z2）≥0，Z2≥B2．条件（i）等价于

对条件（ii）的F′（Z1）进行简单计算可得F′（Z1）＝（1－m）－1＋（1－m）－2m（2＋α1－mα1）［－2＋N－m（mα1＋N－α1）］D1－C［J＋1＋（1－m）－1］ZJ＋（1－m）－11ZI－p／（1－n）2．对 于F′（Z1），当J＋（1－m）－1≤－1时，有

当－1＜J＋（1－m）－1＜0时，有

因为1－2／（mα1＋N）＜m＜1，故－2＋N－m（mα1＋N－α1）＜0，由不等式（13），（14）得D1＜（1－m）／｛m（2＋α1－mα1）［2－N＋m（mα1＋N－α1）］｝．由于p＞［2＋m（mα1＋N）］／（N＋nα2），故

同理可得

因此，对这样的D1，D2＞0以及充分大的B1，B2＞0，可得到不等式（11），（12），从而（¯u，¯v）是问题（2）的全局的上解，定理2得证．

［1］ QI Yuanwei，LEVINE H A．The critical exponent of degenerate parabolic systems［J］．Z Angew Math Phys，1993，44（2）：249－265．

［2］ YANG Jinge，ZHENG Sining，QU Chengyuan．Fujita phenomenon in inhomogeneous fast diffusion system［J］．Z Angew Math Phys，2013，64（2）：311－319．

［3］ 崔世泽，刘玉荣．耦合抛物方程组正解的整体存在性与爆破［J］．扬州大学学报：自然学版，2003，6（3）：14－17，26．

［4］ ZHANG Qi．The quantizing effect of potentials on the critical number of reaction－diffusion equations［J］．J Diff Eqs，2001，170（1）：188－214．

［5］ ISHIGE K．On the Fujita exponent for a semilinear heat equation with a potential term［J］．J Math Anal Appl，2008，344（1）：231－237．

［6］ PINSKY R．The Fujita exponent for semilinear heat equations with quadratically decaying potential or in an exterior domain［J］．J Diff Eqs，2009，246（6）：2561－2576．

［7］ CORTAZAR C，ELGUETA M，ROSSI J D．The blow－up problem for a semilinear parabolic equation with a potential［J］．J Math Anal Appl，2007，335（1）：418－427．

［8］ ISHIGE K，KABEYA Y．Large time behaviors of hot spots for the heat equation with a potential［J］．J Diff Eqs，2008，244（11）：2934－2962．

［9］ ZHANG Qi．A priori estimates and the representation formula for all positive solutions to a semilinear parabolic problem［J］．J Math Anal Appl，1999，232（2）：413－427．

［10］ YANG Chunxiao，ZHAO Lizhong，ZHENG Sining．The critical Fujita exponent for the fast diffusion equation with potential［J］．J Math Anal，2013，398（2）：879－885．