误差理论和概率论在食品化学分析中的应用

翟卉

（农业部乳品质量监督检验测试中心，天津300381）

误差理论和概率论在食品化学分析中的应用

翟卉

（农业部乳品质量监督检验测试中心，天津300381）

食品化学分析中的多次平行测定具有正态分布的概率分布率，测定中7种误差具有各自特征性应用，在规范的化学分析基础上得出更高的准确度和精密度。

误差理论；概率论；食品化学分析

食品化学分析是为了获得食品成分的真值。就食品化学分析的项目来说，可达成千上万个，食品成分包括自然界可食用的所有动物、植物和微生物，同时还包括人为加工所添加剂的食品添加剂以及加工过程中发生的成分变化，涉及几乎有机化学和无机化学学科的所有方面。就食品化学分析的手段来说，除了常规分析化学的重量法、容量法等外，还包括各种光谱、色谱、质谱等仪器分析以及酶联免疫法（ELISA）、聚合酶链反应（PCR）等快速分析，这些分析结果由百分含量直至百亿分之一（0.1 μg/kg）。近年来食品化学分析的迅猛发展，要求充分应用数学工具总结、归纳分析中的规律，结合分析方法寻找科学的分析方案，得出准确的分析结果。相对于化学分析技术而言，数学工具仍显落后，甚至最基础的数学工具还未普及，致使分析结果具有明显的随意性、不可知性，无法解释分析结果正确与否，无法判断可疑结果，无法改进分析技术。因此，分析技术必须与数学工具充分结合，才能达到分析目的。

国际上在食品化学分析中应用数学工具和起源于上世纪初，1927年大卫·波罗特提出测定值的误差分析，首次将误差分为随机误差和系统误差，解释分析结果的准确度；1929年莱劳·特·怀特在误差理论基础上提出最小二乘法，进一步将标准差运用于分析结果的综合判断上；1988年马西摩·司提出多次化学测定遵循高斯分布规律。并将概率论应用于分析结果[1]，奠定了食品化学分析中的应用数学基础，直至1995年国际理论化学和应用护额学联合会（IUPAC）发布“分析化学实验室内部质量控制指南”[2]，总结了以往食品化学分析的应用数学，确定了全世界的基本原则和方法。

1 不同误差在食品化学分析中的应用

测定误差是食品化学分析中不可避免的，其原因是整个分析中每个步骤的不规范因素，包括分析人员的主观因素以及试剂、仪器和环境变化等客观因素。依据其产生机理，可归纳为两类，即随机误差或称偶然误差（random errors）和系统误差（systematic errors）。前者是由分析过程上不确定因素的随机性造成的误差。后者是由保持恒定或以可预知方式变化造成的误差。这两类误差具有不同的特点，因而在化学分析中有不同的用途。

随机误差的特点是：（1）由于造成的因素不可预计，它在分析过程中随机出现，因此无法在化学分析前估计单次分析随机误差的大小；（2）单次分析的随机误差没规律性，可大可小，可正可负。但多次分析的随机误差有抵偿性，其平均值趋于零。这一点为人们所利用，找到消除随机误差的实验方法，也就是说，以足够多的重复分析次数就可使随机误差减小到允许的程度。由于化学分析是多次重复测定，因此不能用单次测定来衡量误差，而用多次测定的综合性标准差（又称标准差、标准偏差、标准离差、均方根差 standard deviation）来衡量，标准差以贝塞尔公式为佳，即

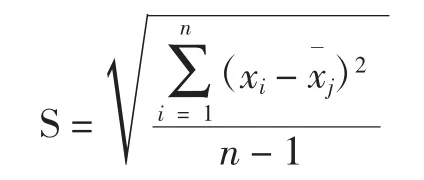
应用标准差就可将重复测定次数与随机误差大小联系起来，这联系是借助于多次重复测定的化学分析概率分布规律，即正态分布（高斯分布）。

系统误差的特点是：（1）造成的因素可预计，在测量之前就存在，能估计其大小；（2）具有叠加性，因此它不能靠多次测量的抵偿来消除，而只能靠对每个因素的校准来削弱或消除。如量具虽温度的变化、分析人员读数的习惯误差、仪器的响应值误差等。

2 化学分析测定值的概率分布

在重复性条件下多次测定的概率分布图为正态分布图或称高斯分布图，如右图所示。即以测定值x作横坐标，出现概率P为纵坐标的分布图。

其概率可用下式表示：

式中：μ为平均值，s为标准差。由图可知测定值概率具有以下性质：

1）高斯分布反映测定值的随机误差，具对称性，抵偿性；

3）标准差愈小，曲线愈陡，随机误差小，精密度高，反之，曲线缓，随机误差大，精密度低；

②应用更精确的测定方法，是每次测定值与多次测定平均值更接近，减小S。例如，用25 mL滴定管时，A级滴定管比B级滴定管更精确，前者的误差为0.04 mL，而后者为0.08 mL。

，即a至 b范围内曲线包含的面积。在化学分析中应用以下三种面积：（a）μ±S测定值范围内出现的概率为68.3%；（b）μ±2S测定值范围内出现的概率为95.0%（精确地说为μ±1.96S）；

（c）μ±3S测定值范围内出现的概率为99.7%。

其中第二种特别有用，它表示在μ±2S范围内测定值出现的概率为95%，仅有5%远离真值（此时以平均值表示）的测定值不在此范围内，左右各2.5%，因此μ±2S范围内的测定值，在全世界被认为是可以视为真值的允许范围（真值为μ，允许范围为2S）[4]。而μ±S要求太苛刻；μ±3S又太松。

为了使S更小，使测定值更接近真值μ，可采取两个方法：

3 几种误差的特殊用途

3.1 绝对误差（absolute error），即测定值与真值之差E =R-τ，在化学分析中应用时，反映了以下含义：

1）当R为一次测定值，则E包含随机误差及系统误差；

2）当R为重复性条件下足够多次测定的平均值时，则E仅为系统误差。这在制定标准方法和科研中很重要，依此排除随机误差，来寻找系统误差，如干扰物质、化学反应完全程度、消化中被测组份损失等。

3）当进行常规测定时，即具上岗证的分析人员应用国家标准方法、检定过的仪器和器皿进行测定时，则系统误差视为零（实际上是在允许范围之内的数值），这时在重复性条件下足够多次测定又消除了随机误差，所以E=0，μ=τ，即在以上条件下测定的算术平均值μ视为真值。

所谓重复性条件即在相同测量条件下（人、仪器、方法、环境）对同一样品同一组分连续测定。

3.2 相对误差（relative error），即绝对误差对真值的百分率，在化学分析中应用时，除了与绝对误差的三点含义相同外。它反映的不是量值大小，而是相对百分率，用来比较不同次测定、样本或本底值等的测定误差。

3.3 算术平均偏差（arithmetic mean of bias），即i次测定偏差的算术平均数：

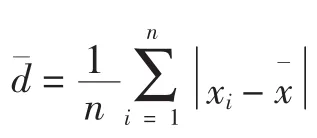
在化学分析中应用时，反映了以下含义：

1）衡量随机误差大小，d小，随机误差小，如图A、B所示，在概率分布图上表现为曲线陡；而d大，随机误差大，如图C、D所示，曲线缓。

3.4 相对标准差（relative standard deviation），又称变异系数（coefficient of variation）即标准差的平均值

在化学分析中应用时，反映了以下含义：它以相对百分率表示标准差，而不是绝对数值，因此可以比较不同测定平均值的随机误差大小，或精密度大小，或高斯分布曲线的陡缓。

3.5 极差R（maximum diffence），即一组测定值中最大值与最小值之差值Xmax—Xmin。在化学分析中用于数据检验，如目前世界通用的狄克逊检验（Dixon test），还可用于F检验。例如，当标定一个标准滴定溶液时，得出10个测定浓度。其=0.101 2，S=0.003 6，R=0.012，单位为mol/mL。在用于滴定（或仪器法作内标）时，必须从样本的实测值推断总体的真值。推断的方法如下：

1）将样本的算术平均值作为总体平均值μ的估计值，该10个测定值的平均值为0.101 2；

2）选择1个置信概率，一般γ=0.95，也称显著性水平0.05；

3）计算置信区间，从高斯分布图可知积分计算很麻烦，因此创造了一个t检验（双侧检验）和F检验（单侧检验）的表格，便于查表计算。

（a）t检验计算，由t检验表可知n=10，γ=0.95时，0.003 6=（0.101 2±0.002 6）mol/mL=0.098 6 mol/mL～0.103 8 mol/mL。

这说明尽管标定浓度平均值为0.101 2 mol/mL，而根据10次标定的分散性（由S、R反映）标液的真实浓度并不是0.101 2 mol/mL（这仅是一个近似值），而应该是（0.1012±0.0026）mol/mL范围内（出现的概率为0.95，是可值得信赖，因仅有5%的可能是不在这范围内）。由这标准滴定溶液的置信限0.002 6 mol/mL可推断用其滴定（如测定、加标）发生的误差。

（b）F检验计算，由F检验表可知n=10，γ=0.95时，f=0.230置信区间x±fR=0.101 2±0.230×0.012=（0.101 2±0.002 8）mol/mL=0.098 4 mol/mL～0.1040 mol/ mL，两种计算方法结果很一致。

[1]Massimo C,J T Chayes L.Chayes Gaussian fluctuations of Connectivities in the Subcritical Regime of Percolation[J].Probability Theory and Related Fields,1988,1:209-341

[2]IUPAC.Harmonized Guildlines for Internal Quality Control in Analitical Chemistry Laboratory[J].Pure&Appl Chem,1995,67:649-666

Error Theory and Probability Used in Food Chemical Analysis

ZHAI Hui
（Dairy Monitoring Center of Department od Agriculture，Tianjin 300381，China）

Multi-determinations of food chemical analysis are characterized by Gauss Distribution of probability. The involving seven errors of different use in chemical analysis are aimed to improve determination accuracy and precision.

error theory；probability；food chemical analysis

10.3969/j.issn.1005-6521.2014.19.041

2014-06-17

翟卉（1963—），女（汉），工程师，本科，研究方向：食品监督及检验。