一类分数阶积分多点边值问题正解的存在性

戴 琛

(苏州高等幼儿师范学校，江苏苏州 215008)

一类分数阶积分多点边值问题正解的存在性

戴 琛

(苏州高等幼儿师范学校，江苏苏州 215008)

本文运用上下解和不动点定理的方法对一类分数阶积分多点边值问题进行研究，通过对格林公式性质的研究和分析得到了该问题正解的存在性。

分数阶微分方程；不动点定理；上下解；正解

我们研究如下形式的一类带有p-Laplacian算子的分数阶m多点边值问题：

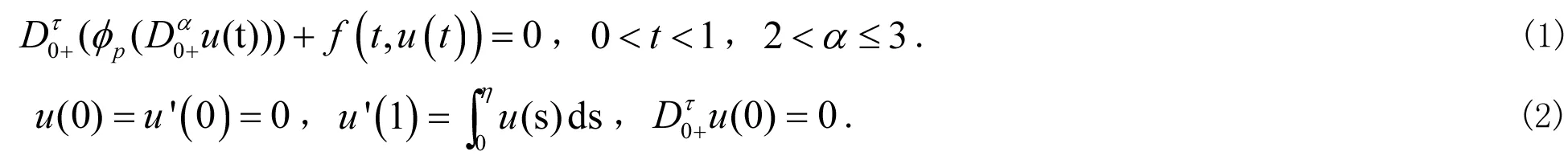
近年来，分数阶积分理论因其在物理、化学、机械、工程等领域的广泛应用而受到国内外许多学者的关注.分数阶微分方程解的存在性研究是微分方程定性理论的重要内容之一，也是进一步研究分数阶微分方程理论及其应用的重要基础.随着分数阶微分方程理论的不断发展，关于分数阶微分方程初值问题解的在存性研究有比较丰富的结果[1-11]，文献[2]运用锥拉伸与锥压缩不动点理论讨论了含参数的分数阶两点边值问题正解的存在与不存在性，文献[9]运用上下解方法和不动点定理，研究了一类分数阶两点边值问题正解的存在性，BashirAhmad在文献[5]中用压缩映射不动点定理，研究了一类分数阶反周期边值问题解的存在性.张淑琴在文[7]中利用不动点定理，研究了一类分数阶高阶奇异微分方程边值问题正解的存在性.

引理1 设0<ηα<α(α-1). 如果h∈C[0,1]，那么

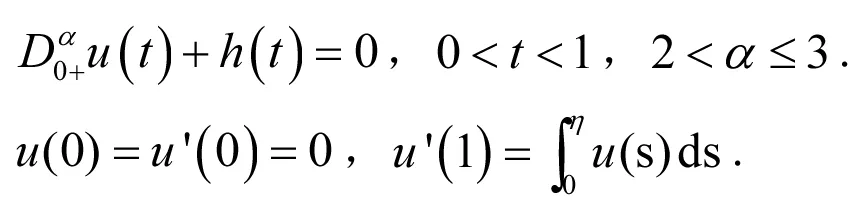
有唯一的解

(3)

其中G(t,s)=G1(t,s)+G2(t,s)，且

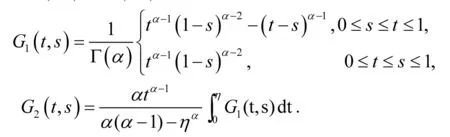
引理2 边值问题(1)～(2)等价于下面的积分方程

.

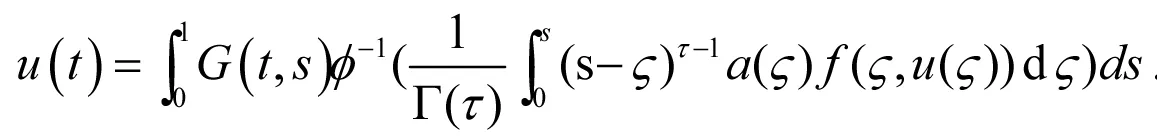
(4)

在这部分，通过上下解的方法建立问题(1)～(2)中正解的存在性. 假设f:[0,1]×[0,+∞)→[0,+∞)是连续函数.

注：显然，由引理1.1和引理1.2可知，当h(t)≥0时，u(t)≥0.

定义4 如果θ(t)∈C[0,1]且θ(t)满足

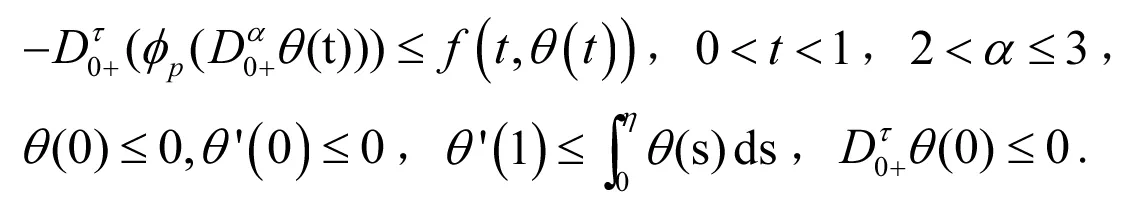
称θ(t)是问题(1)～(2)中的下解.

定义5 如果γ(t)∈C[0,1]且γ(t)满足

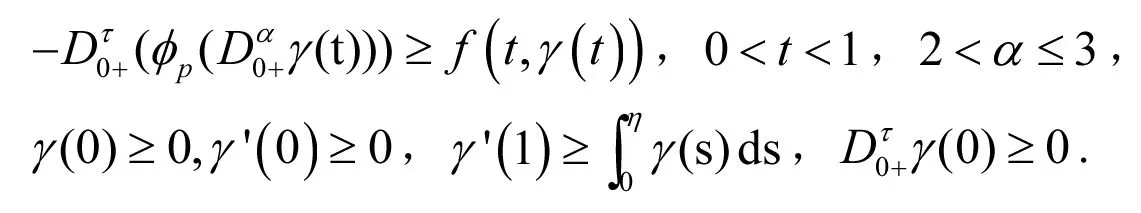
称γ(t)是定义问题(1)～(2)中的上解.

本文的主要结论如下：

定理6 如果u(t)满足下列条件：(Hf)f(t,u)∈C([0,1]×[0,+∞),R+)对变量u是单调非增函数，f(t,ρ(t))≠0，∀t∈(0,1)，存在一个常数μ<1，使得kμf(t,u)≤f(t,ku) ，∀0≤k≤1，那么，问题(1)～(2)存在正解u(t).

由引理2，可知g(t)是下列方程的解

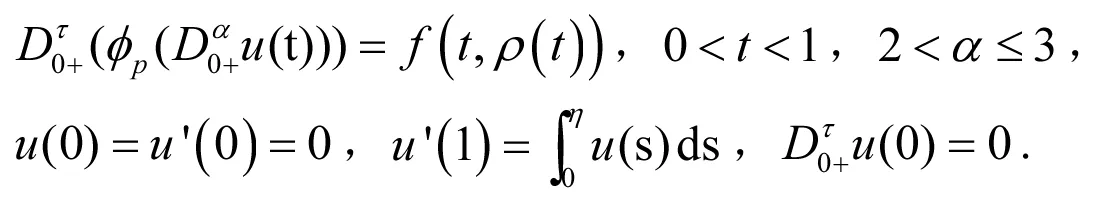
从引理3的结论可知a1ρ(t)≤g(t)≤a2ρ(t)，∀t∈[0,1].

因此，利用定理6的假设条件可知

这意味着

显然，函数θ(t)=k1g(t)和γ(t)=k2g(t)满足边界条件(2).因此，α(t)=k1g(t)，β(t)=k2g(t)分别是问题(1)～(2)的下解和上解.

下面证明问题

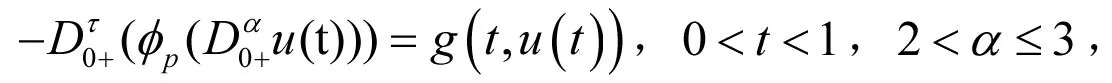
(5)

(6)

有解，其中

算子T:C[0,1]→[0,1]是连续的，那么G(t,s)和g(t,u(t))也是连续的函数. 由Arzela-Ascoli定理可知，T是一个紧算子.因此，由Leray-Schauder的不定点定理可以知道，算子T是有一个不动点，即问题(5)～(6)有解.

最后，证明问题(1)～(2)存在正解.

假设u*(f)是问题(5)～(6)的一个解. 由于f(t,u)是关于u的单调非增函数，则

那么

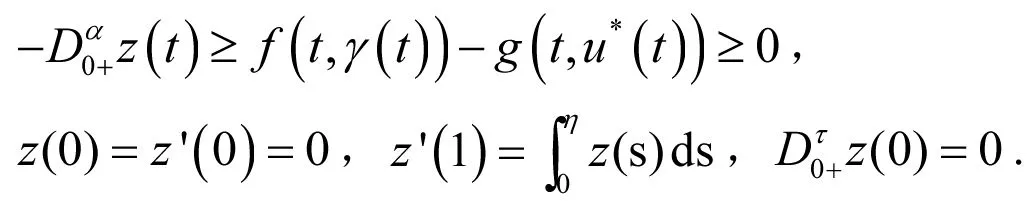
[1]Podlubn Y I.Fractional Differential Equations,Mathematics in Science and Engineering[M].New York,London,Toronto:Academic Press,1999.

[2]Gan S Q.Dissipativity of -methods for Nonlinear Volterra Delay- integro- differential Equations[J].J Comput.Appl.Math,2007,206:98-107.

[3]Z.Bai,Y.Zhang.The existence of solutions for a factional multi-point boundary value problem[J].Appl. Math.Comput.,2010(60):2364-2372.

[4]Z.B.Bai,T.Qiu.Existence of positive solution for singular fractional differential equation[J].Appl.Math. Lett.,2009,215:2761-2767.

[5]Bashir Ahmad. Existence of solutions for fractional differential equations of order q∈(2,3] with anti-periodic boundary conditions[J].J Appl.Math.Comput,2010,34:385-391.

[6]X.W.Su.Boundary value problem for a coupled system of nonlinear fractional differential equations[J].Appl. Math.Lett.,2009,22:64-69.

[7]S.Q.Zang.Positive solutions to singular boundary value problem for nonlinear fractional differential equation[J].Comput.Math.Appl.2010,59:1300-1309.

[8]Z.B.Bai,Y.Zhang.The existence of solutions for a factional multi-point boundary value problem[J]. Appl.Math.Comput,2010,60:2364-2372.

[9]S.H.Liang,Y.Song.Existence and uniqueness of positive solutions to nonlinear fractional differential equation with integral boundary conditions[J].Lithuanian Mathematical Journal,2012,52:62-76.

[10]Y.H.Zhang,Z.Bai.Existence of positive solutions for s nonlinear fractional three-point boundary value problen at resonance[J].Appl.Math.Comput.DOI:10.1007/s12190-010-0411-x.

[11]W.H.Jiang.The existence of solutions to boundary value problems of fractional differential equations at resonance[J].Nonlinear Anal.,2011(74):1987-1994.

Existence of Positive Solutions to the Multi-point Boundary Value Problems of Fractional Integral of the Same Category

DAI Chen

(Suzhou Higher Infant Normal School, Suzhou Jiangsu 215008, China)

This paper applies the methods of upper and lower solutions and the fixed point theorem to the study of multi- point boundary value problems of fractional integral of the same category. Through the research and the analysis of the Green formula properties, the existence of positive solutions to the problems is obtained.

Fractional differential equation; Fixed-point theorem; Lower and upper solution; Positive solutions

2014-01-07

戴 琛(1980- )，女，江苏苏州人，苏州高等幼儿师范学校讲师，从事应用数学研究。

O175

A

2095-7602(2014)04-0003-04