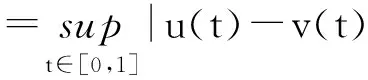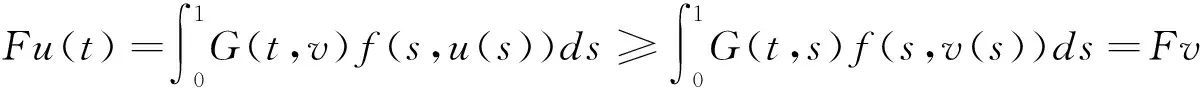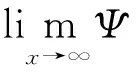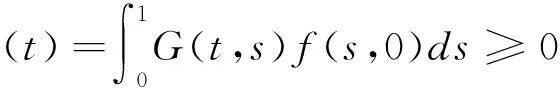二阶常微分方程边值问题正解的存在性与唯一性
2014-07-01刘艳
刘 艳
(苏州高等幼儿师范学校,江苏苏州 215008)
二阶常微分方程边值问题正解的存在性与唯一性
刘 艳
(苏州高等幼儿师范学校,江苏苏州 215008)
本文利用偏序集上的不动点定理,证明一类二阶常微分方程边值问题正解的存在性,通过对格林公式的分析获得了唯一性结果。
边值问题;偏序集;正解;唯一性
我们将研究如下的二阶常微分方程多点边值问题:
u″+f(t,u)=0,0 (1) αu(0)-βu′(1)=0,γu(0)+δu′(1)=0. (2) 其中,α,β,γ,δ≥0,且αγ+αδ+γδ>0. 关于二阶多点边值问题,最早是1987年由Il’in和Moiseev开始研究的,受Bitsadze和 Samarskii关于非局部的线性椭圆边界值问题的工作的启发,他们研究了二阶线性微分方程的多点边值问题,因为在理论和实际应用中,二阶非线性微分方程的多点边值问题更有意义.之后有许多数学家都围绕二阶非线性常微分多点边值问题进行研究,其研究方法主要是使用不动点理论[1-4].虽然一些作者已经证明出关于非线性二阶多点边值问题解的存在性和多解性,但是对于多点边值解的存在性和唯一性的结果相对较少. 因此,本文运用偏序集上的不动点定理研究二阶多点边值问题(1)和(2),以获得其正解的存在性和唯一性的结果.最近关于偏序集上的不动点定理见文献[5-9]. 定理1.1[9]设(E,≤)是偏序集,在E中存在一个度量单位d,则(E,d)是一个完备的度量空间。假设E满足下列条件: 如果{xn}在E中为一个单调非增数列,且xn→x, 那么xn≤x,∀n∈N. (3) 如果我们考虑(E,≤)满足下面条件: 由于x和y是可以比较的,根据x,y∈E且存在z∈E. (4) 定理1.2[5]假设定理1.1的条件和(4)成立,则得到边值问题正解的唯一性. 这里 (5) x,y∈C[0,1],x≤y⟺x(t)≤y(t),t∈[0,1]. 定理2.1 假设下列条件成立:(C1)当f(t,u(t))≠0,其中t∈Z⊂[0,1],μ(z)>0(μ指的是测度)时,那么f:[0,1]×[0,+∞)→[0,+∞)是关于第二个变量的单调非增的连续函数;(C2)当u,v∈[0,+∞),且μ≥v,t∈[0,1]时,存在0<λ 由条件(C1)可知F(K)⊂K.最后将验证满足定理1.1和定理1.2所有的条件. 一方面,当u,v∈K且u≥v时,由条件(C1)可知 另一方面,当u≥v时,由条件(C2)可知 由于函数g(x)=ln(x+1)单调非减,从而可知 由定理1.1可知,问题(1)~(2)至少有一个正解.由于(K,≤)满足条件(4),则由定理1.2可知问题(1)~(2)具有唯一的正解. [1]Z.Bai,Z.Du.Positive solutions for some second-order four-point boundary value problems[J].J. Math. Anal. Appl.,2007,330:34-50. [2]E.R.Kaufmann,N.Kosmatov.A second order singular boundary value problem[J]. Compu.Math.Appl.,2004,47:1317-1326. [3]C.P.Gupta.Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equations[J].J.Math.Anal.Appl.,1998,168:540-551. [4]郭大钧.非线性泛函分析[M].济南:山东科学技术出版社,1985. [5]Nieto,J.J.,Rodríguez-López,R.:Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations[J].2005(22):223-239. [6]Nieto,J.J.,Rodríguez-López,R.:Fixed point theorems in ordered abstract spaces[J].Proc.Am. Math.Soc.,2007, 135(8):2505-2517. [7]Podlubny.I.Fractional Differential Equations[J].Mathematics in Sciences and Engineering.Academic Press, San Diego,1999,198. [8]O’Regan,D.,Petrusel.A.:Fixed point theorems for generalized contractions in ordered metric spaces[J].J. Math. Anal.Appl.2008,341:1241-1252. [9]Harjani,J.,Sadarangani.K.:Fixed point theorems for weakly contractive mappings in partially ordered sets[J]. Nonlinear Anal.2009,71:3403-3410. Existence and Uniqueness of Positive Solutions to the Multi-point Boundary Value Problems of Second- Order Ordinary Differential Equations LIU Yan (Suzhou Higher Infant Normal School,Suzhou Jiangsu 215008,China) In this paper, we will study the existence of positive solutions for second order ordinary differential equation boundary value problem by using the fixed-point theorem in partially ordered sets. And through the analysis of Green’s formula the uniqueness is obtained. boundary value problems; partially ordered sets; positive solution; uniqueness 2014-03-20 刘 艳(1977- ),女,江苏苏州人,苏州高等幼儿师范学校高级讲师,从事应用数学研究。 O175 A 2095-7602(2014)04-0001-031 预备引理
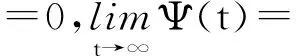
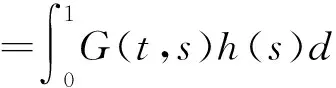
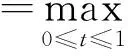
2 主要结论及其证明