力-位移分控多点成形鞍面回弹的数值模拟研究

李 颖，王卫卫，贾彬彬，于静泊

（哈尔滨工业大学（威海），山东 威海264209）

0 引言

多点成形是由一系列规则排列、高度可调的基本体形成离散曲面代替传统模具进行三维曲面成形的板材柔性加工技术[1]。由于基本体与板材接触面积的大幅度减少，常导致曲面成形时板材厚向约束不足，容易产生成形缺陷，如压痕、起皱、回弹等[2]。利用力-位移分控的多点成形方法，可以很好地克服成形失稳、起皱等缺陷。但回弹现象是影响其成形质量的一个重要因素。

因此，在力-位移分控的多点成形中，研究回弹的影响因素对成形过程的控制和成形质量的提高具有重要的指导意义。文献[3-5]分别对不同参数的球面、圆柱面和帆面进行了力-位移分控的多点成形数值模拟，并利用经典回弹理论分析了其回弹的影响因素。本文则利用力-位移分控的多点成形方法，对不同参数的马鞍面进行数值模拟，并研究了回弹对板材成形性能的影响。

1 力-位移分控多点成形简介

力-位移分控的多点成形方法是通过分别控制板材两侧点状模具群的作用力或位移量来进行成形，能保证在整个成形过程中，板材始终处于上下点状模具群的夹持约束中，实现曲面板材的有约束成形。其工作原理如图1 所示。上下基本体的行程是由上基本体的螺杆长度控制的，而成形过程中板材受到的成形作用力是由下基本体的液压缸控制的。从而使成形过程中的基本体的位移和成形作用力分别由上下基本体控制。

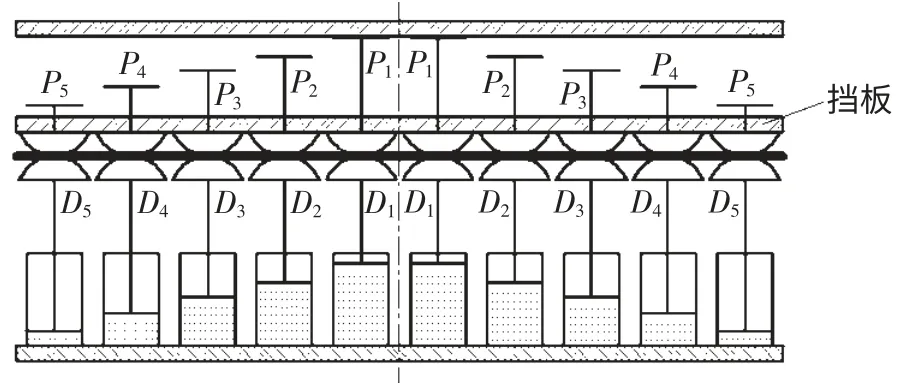
图1 力-位移分控多点成形工作原理图

2 有限元模拟

2.1 曲面造型

一半径为R，圆心在（0，0，a）的圆（图2a），使其绕y 轴旋转一周，可以得到一个圆环曲面，其方程为当a≠0 时，圆环的内半环部分（图2b）相当于一个鞍面，鞍面方程可写为[6]

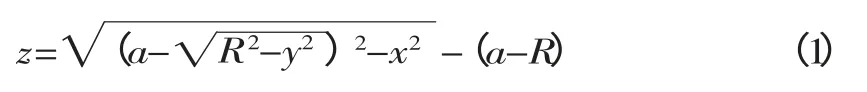
图2 鞍面示意图

2.2 基本算法的选择

ANSYS/LS-DYNA 将LS-DYNA 和ANSYS 程序强大的前后处理结合起来。LS-DYNA 的显式算法能快速求解瞬时大变形力学、大变形和多重非线性准静态问题以及复杂的接触碰撞问题。针对力-位移分控多点成形的特点，加载冲压过程采用显式算法，回弹过程采用隐式算法，不但计算精度高，并且计算时间短。

2.2.1 加载过程采用显式算法

在动力学问题中，如果采用显式算法进行分析时，可建立虚功方程为

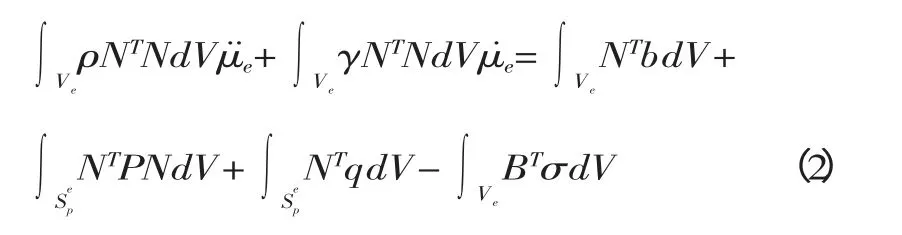
式中：ρ——质量密度；

γ——阻尼系数；

S——表面积，S=Sp+Sc+Su；

p——Sp上给定表面力；

b——单位质量上作用体积力；

q——Sc另一物体接触的接触表面力；

V——体积。

将式（2）应用于离散后的所有单元，并将所有的单元方程集合构成整体有限元方程

式中：M——质量矩阵；

C——阻尼矩阵；

U¨——节点加速度；

U˙——节点速度向量；

P——节点外力矢量；

F——节点内力矢量。

2.2.2 卸载过程采用隐式算法

弹塑性变形体内任一单元的虚功方程的矩阵形式为

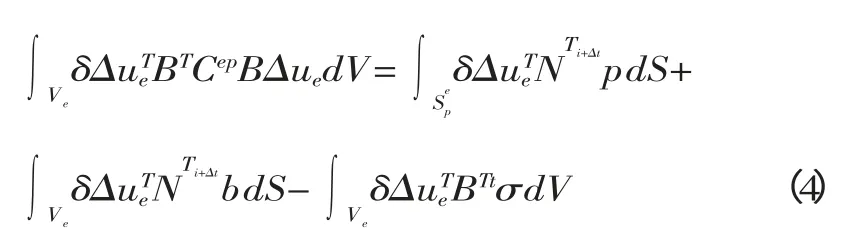
式中：Cep——增量弹塑性矩阵。

由式（2）得到整个变形体有限元方程

式中：Kt——t 时刻的刚度矩阵；

Ut+1——t+1 时刻位移增量；

Pt——t 时刻整体节点外力向量；

Ft——t 时刻整体节点内力向量。

2.3 有限元模型基本设置

力-位移分控的多点成形数值模拟在显式的冲压成形阶段采用的是BWC 壳单元，而在隐式回弹阶段采用的是SHELL181 单元。成形的板材采用的是Q235 钢板，故采用满足Hill 厚向异性屈服准则的弹塑性非线性材料模型[7]。板料和模具的接触采用SURFACE_TO_SURFACE（STS），接触力计算采用罚函数法。刚性面与下基本体之间的接触定义为刚性面接触RIGID BODY TO RIGID BODY（ROTR），通过定义力-变形曲线阻止下基本体的穿透。

本文采用上、下基本体群各为10×10，基本体间距20mm，基本体球头直径20mm，板料尺寸200mm×200 mm，板料厚度分别1mm、1.5mm、2mm、2.5 mm、3mm。有限元模型如图3 所示。

图3 有限元模型

3 回弹的表示及计算

3.1 回弹的表示方法

板料的弯曲成形总是伴有弹性变形的，所以卸载后，总变形中的弹性变形部分立即恢复，引起板料的回弹，其结果表现在弯曲件曲率和角度的变化。

目前，回弹的表示方法有很多，主要有经典冲压理论的回弹表示法、回弹比及回弹角等。为了直观反映回弹的大小，本文采用回弹角来表示成形前后的回弹量：

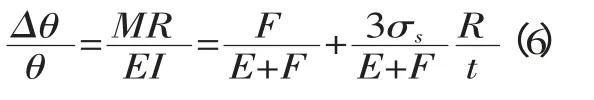
σs——材料屈服应力，Pa；

R——板材目标弯曲半径，m；

t——板材的厚度，m；

E——弹性模量，Pa；

F——硬化模量，Pa。

也可用下式表示：

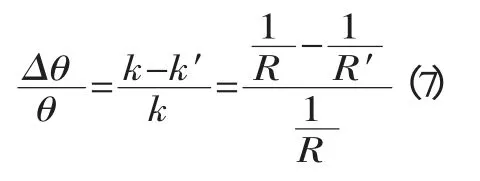
式中：k——板材回弹前的平均曲率；

k′——板材回弹后的平均曲率；

R——板材回弹前的平均曲率半径；

R′——板材回弹后的平均曲率半径。

3.2 回弹的相关计算

以板材回弹后的平均曲率半径k′为例进行计算。

在数值模拟的建模过程中，为简化模型，取四分之一模型，则模型的尺寸为100mm×100mm，网格划分为2.5mm，这样模型每条边上的节点数为41 个（分别编号为1～41）。考虑到直边效应和边缘起皱情况，进行回弹计算时，去除成形缺陷明显的第一个节点和最后四个节点，共剩下36 个节点（即编号为2～37），平均分成两组，第一组为编号为2～19 的节点，第二组为编号为20～37 的节点，任取第一组节点an以及与之间隔十八个点的an+18, 从ANSYS 中导出对应的坐标，如下所示：

建模中选择板料的中心点为坐标原点，若取y=0 方向为研究对象，成形结束后，各个节点x 坐标是一个定值，理想情况下z 也是定值，但是由于成形缺陷的存在，z 是随节点变化的。因为是在xOz 平面内，所以y 是定值，为减少偏差，应对其计算18 次，取平均数后才求得其回弹后的平均曲率半径R′：

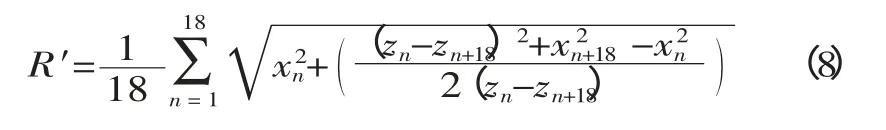
对板材回弹前的平均曲率半径也可用上式求得。

4 回弹影响因素分析

回弹是板材整个成形过程中的积累效应，与材料特性、模具几何形状、摩擦接触及成形力等很多因素有关，所以在板材成形中，回弹是非常复杂的问题。本文主要从成形板材的曲率半径以及板材厚度这两个方面来讨论对回弹的影响。

4.1 成形曲率半径对回弹量的影响

对于鞍面的形状参数a 和R，它们分别决定了y=0 和x=0 这两个方向的曲率半径。其中，x=0（即y轴）的理论曲率半径为R，而y=0（即x 轴）的理论曲率半径为a-R。本文先对y=0 方向的回弹进行分析，令x=0 方向的曲率半径不变分别设为240mm、280mm 和320mm，改变y=0 方向的曲率半径即为变化a 值，具体参数为a480、a720 以及a960，成形力均为1000N，对其进行作图分析，如图4a、b、c 所示。

由图可见，在成形力为1000N，且板厚及曲率半径R 相同时，随着a 值的增大即y=0 方向曲率半径的增加，其回弹量呈现增长的趋势。分析原因：理论上说，回弹量的大小与成形后板料内部应力有着直接的关系，材料内部应力的大小又由板料变形量决定，曲率半径的大小决定了变形量的大小。当曲率半径较小时，材料的变形量大，成形结束后塑性变形占总变形的比例也越大。与之相反，当曲率半径较大时，板材外表面的纵切向变形程度减小，其中塑性变形和弹性变形成分相应都减小，但在总变形中弹性变形比例比较大，因此回弹也比较大，卸载后弹性变形消除，因而回弹量增大[8]。模拟结果进一步论证了该结论。

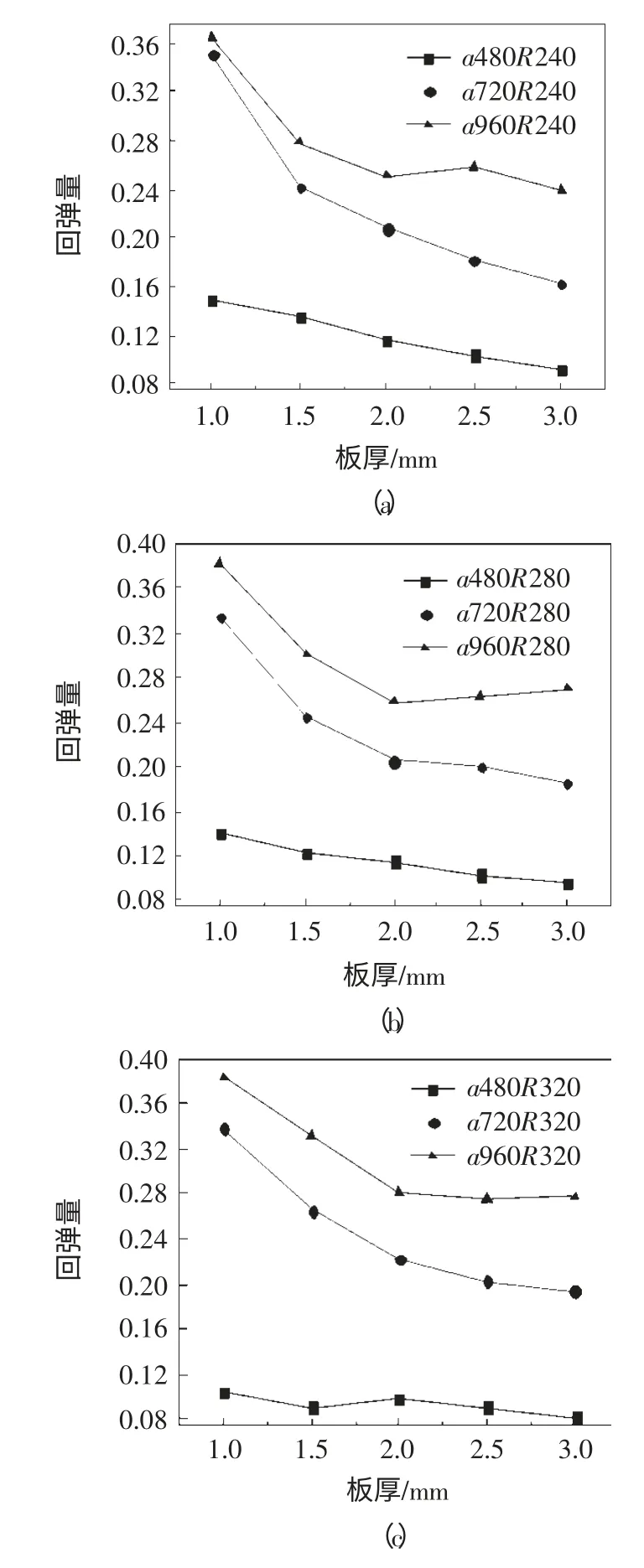
图4 回弹量随曲率半径变化情况（y=0）

x=0 方向曲率半径对其回弹的影响则如图5a、b、c 所示。由图可见，在成形力为1000N 时，x=0 方向均发生了负回弹，可见，x=0 方向的回弹是受到了y=0 方向回弹的影响。图5a 中，当a=480 时，随着R值的增大即x=0 方向曲率半径的增加，其回弹量呈现减小的趋势。究其原因：一方面，随着R 值的增大，x=0 方向所产生的正回弹量有所增加，更多地抵消了负回弹；另一方面，随着R 值的增大，即a-R 减小，则y=0 方向所产生的回弹减小，对x=0 方向的负回弹影响也相应减小。图5b、c 中，当a 为720 及960 时，随着R 值的增大即x=0 方向曲率半径的增加，其回弹则呈现出与a=480 相反的趋势，即负回弹增大。分析原因：

4.2 板厚对回弹量的影响

为了研究板厚对回弹量的影响，本文选取了鞍面参数为a720，在成形力为1000N 下，对应于5 个板厚（1mm、1.5mm、2mm、2.5mm、3mm）的数值模拟结果，并以y=0 和x=0（针对1/4 模型而言）的两条边作为研究对象，如图6、7 所示。

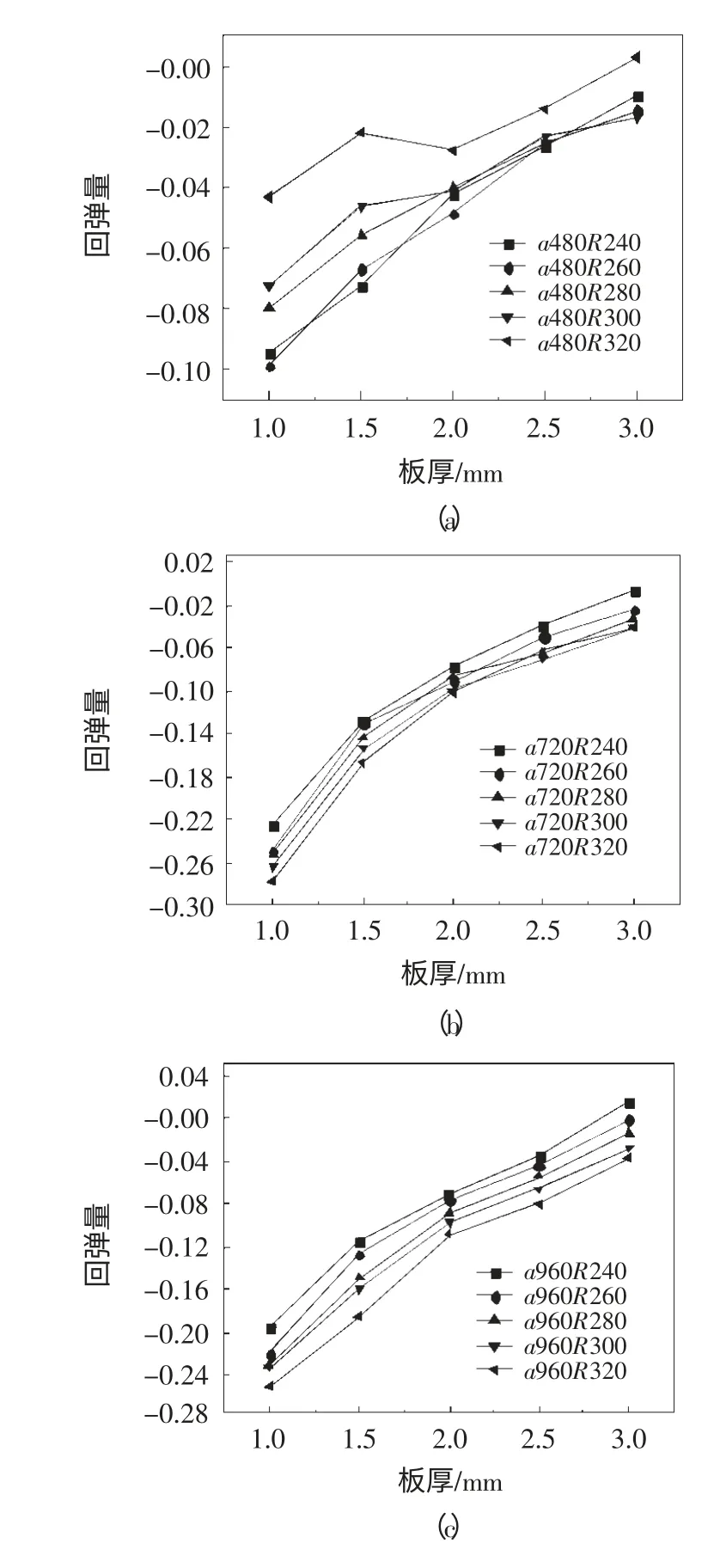
图5 回弹量随曲率半径变化情况（x=0）

由图显然可见，在成形力1000N 下，无论是x=0方向还是y=0 方向，随着板厚的增加，其回弹量都在减小。由于板厚越厚，板材的变形抗力越大，成形时所需要加载的弯矩也越大，因此卸载后的回弹量则越小[9]。同样的，鞍面在x=0 方向收到了y=0 方向回弹的影响而产生了负回弹。从图10、11 可以分析出，随着板厚的增加，x=0 方向上的回弹受到y=0 方向回弹的影响越小。也就是说，板厚越小，则y=0 方向对x=0 方向回弹的影响越显著。

5 结论

（1）双曲率马鞍面在发生回弹时，随着曲率半径的增大，则该方向的回弹也在增大。

图6 回弹量随板厚变化情况（y=0）

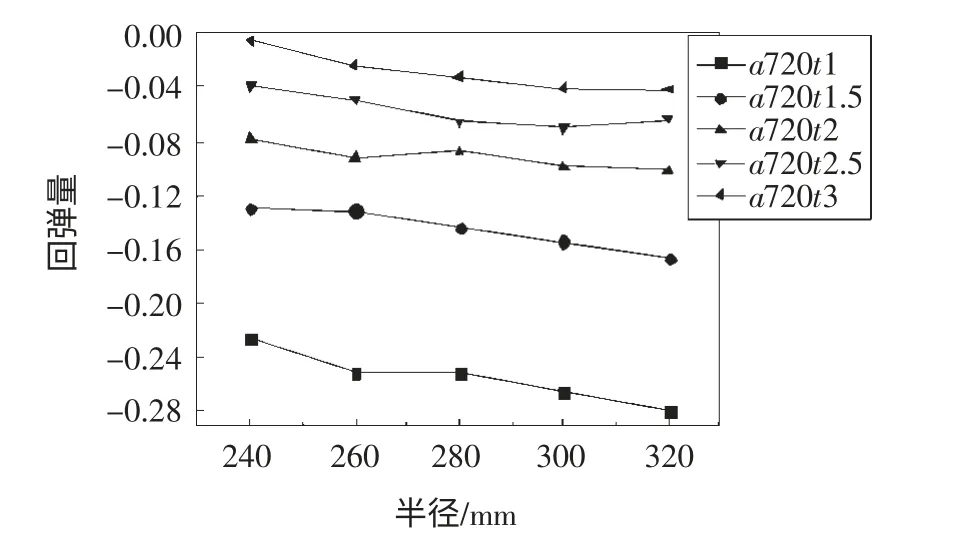
图7 回弹量随板厚变化情况（x=0）

（2）双曲率马鞍面在发生回弹时，随着板厚的增大，则两个方向的回弹均在减小。且起主导作用的方向对另一方向的回弹影响会随着板厚的减小而越显著。

[1]Li M Z.Cai Z Y,Sui Z,etc.Multi-point forming technology for sheetmetal[J].Journal of Materials Proceessing Technology,2002,129（1-3）:333-338.

[2]李明哲，中村敬一.多点成形中缺陷的发生及控制[C]//日本第43回塑性加工联合讲演会论文集.京都，1992.

[3]于静泊，王卫卫，贾彬彬.力-位移分控多点成形球面回弹的数值模拟[J].煤矿机械，2009，03（3）：61-63.

[4]崔爱爱，王卫卫，陈 泽，等.圆柱面力-位移分控多点成形的数值模拟研究[J].锻压装备与制造技术，2011，46（5）：91-95.

[5]Wang Weiwei,Chen Ze,etc（2012）Numerical simulation on the multi-point forming of sail surfaces under force-displacement separated control.Applied Mechanics and Materials,217-219,1959.

[6]高东强，胡 林.基于ISDX 的双曲抛物面造型[J].制造业信息化，2005，11：112-113.

[7]Hill R.A Theory of the Yielding and Plastic Flow of Anisotropic Metals.Roy.Soc.，London Proc.，1948.

[8]杨建鸣，郝 洁，郭晓妮.基于ANSYS/LS—DYNA 的板材多点成形中回弹的数值模拟[J].装备制造技术，2011，（2）：1-3.

[9]麻桂艳，付文智，李明哲.中厚板多点成形中回弹的数值模拟[J].锻压技术，2006，（4）：141-144.