附加交易费用的动态投资组合鲁棒策略

郑 冬，梁锡坤

（杭州师范大学杭州国际服务工程学院，浙江杭州310036）

附加交易费用的动态投资组合鲁棒策略

郑 冬，梁锡坤

（杭州师范大学杭州国际服务工程学院，浙江杭州310036）

在风险资产期望收益和协方差矩阵不确定的情况下，研究了附加交易费用的动态投资组合鲁棒策略，并运用LMI方法就其实证分析所得到的结果分别与基准组合、有效边界组合模型的结果进行了比较.结果表明，附加交易费用的动态投资组合鲁棒策略所得到的权重分配更加合理，所得到的最终收益也优于其他组合模型，而且附加交易费用后的模型更加贴近于大额投资情况下金融市场的实际交易.

均值－方差模型；投资组合优化；跟踪误差；鲁棒；交易费用

0 引言

自H.M.Markowitz于1952年提出均值－方差投资组合以来，其理论备受推崇，原因取决于它不仅奠定了现代金融学的基础，而且建立了更加贴近于现实市场需求的模型［1］.在随后的时间里，诸多学者针对该模型的特点进行了相应的扩展和完善［2－15］.Lobo在均值－方差模型的基础之上给出了鲁棒的投资组合优化方法［2］，M.C.Pinara等人研究了在风险金融投资组合当中的鲁棒收益机会问题［3］.如今，面对着具有风险的交易市场，资金所有权与投资管理权分离的情况日渐增多，R.Roll等人将这一理论与跟踪误差的投资组合优化相结合对此问题进行了分析［9］，D.L.V.Costa等人根据拟定的协方差矩阵和收益率的期望值在二者都不确定的情况下，通过线性矩阵不等式的方法对跟踪误差鲁棒投资组合的问题进行了相应的研究［11］.其他学者也研究了交易过程中的交易费用问题，D.Bertsimas等人在解决多阶段鲁棒投资组合选择问题中涉及了交易费用［13］，E.Erdogany也在创建的积极投资组合管理的鲁棒投资组合选择模型的基础之上分析了分段的凸交易费用函数问题［14］，Xue等人研究了交易费用为二次凹函数情况下的鲁棒投资组合问题［15］.

本文在不确定的市场条件下，通过鲁棒投资组合优化策略，对基于交易费用的风险资产跟踪误差鲁棒最优投资组合选择的问题进行了研究（这里只考虑风险的存在，且其收益率、协方差矩阵均属于已知凸集），最后运用线性矩阵不等式方法，依据深圳证券交易市场的交易数据，进行了实证分析，并与基准组合、有效边界组合的结果进行了对比.

1 模型介绍

拟定一个市场存在n种风险，其收益列向量W＝（w1，w2，…，wn）′，收益的期望列向量与协方差矩阵分别为μ和V.风险投资组合的权重向量z＝（z1，z2，…，zn）′，交易费用P（z）＝（P1（z1），P2（z1），…，Pn（zn））′，则风险资产的净投资组合权重¯z＝z－P（z）＝（¯z1，¯z2，…，¯zn）′，风险资产的总收益Rμ（z）＝

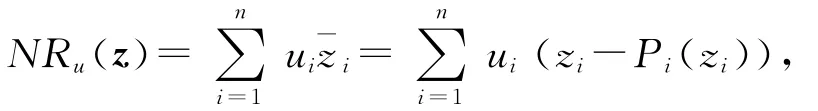
因固定费可剔除，这里将线性交易费用函数设为

所谓跟踪误差指的是投资组合的实际收益与预期的基准收益之差.设基准投资组合为zB＝（zB1，zB2，…，zBn）′，则跟踪误差的期望值就是投资组合的相对收益，表示为β（z）＝（z－zB）′u，跟踪误差的方差为σ2（z）＝（z－zB）′G（z－zB）.

在风险资产市场中，投资者都希望各自投资组合的相对风险尽可能的小，并且其相对收益又尽可能的大，从而实现最好的绩效.但通常对于像这种极大收益极小风险的双目标决策模型是无解的，跟踪误差投资组合的问题可以写为分别给定在期望收益和风险条件下的两种模型.［10］

（1）在确保达到相对收益目标的情况下，最小化风险：

这里β0是事先设定的相对目标收益，

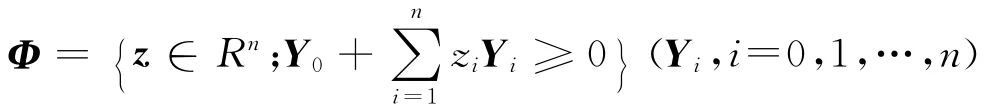
是已知的对称矩阵.

（2）在确保小于相对风险的情况下，最大化收益

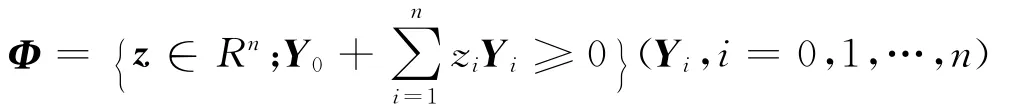
是已知的对称矩阵.

显然，这两个模型是等效的，所以，无论投资管理者选用模型（2）或是模型（3），只要对投资组合配置的相对收益或者相对风险配置是有效的，就可以得到相同的投资组合权重向量.本文仅针对于模型（3）进行讨论.

2 基于线性矩阵不等式的鲁棒策略求解方法

在风险资产交易市场中，由于协方差和期望收益会随着金融市场环境的不同而作无规律的变化，所以需要通过拟定多个输入参数协方差和期望收益来描述未来市场变化的情景集（凸集）的不确定性.

基于上述条件，通过以线性矩阵不等式形式给出只有n种风险资产存在情况下的鲁棒优化模型如下：

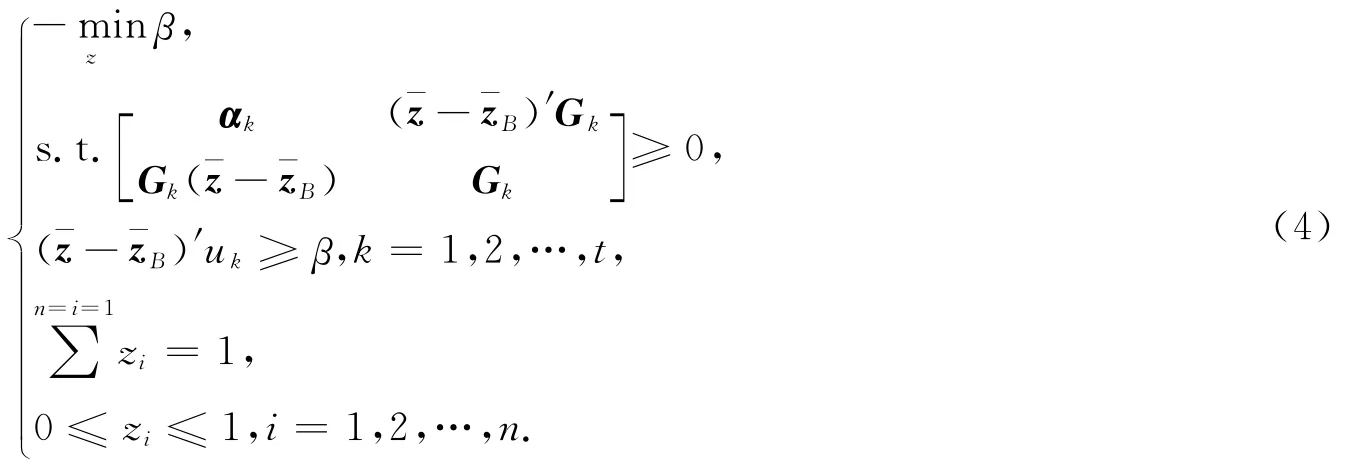
在最后求解的过程当中，我们可以通过LMI的方法得到模型的鲁棒优化解，即在跟踪误差波动最大的条件下，求出对应的投资组合，保证期望收益最大.

3 实证分析

本文采用深圳证券市场的交易数据，利用鲁棒策略进行实证分析，并将其结果与基准组合和有效边界组合的结果相比较，以下实证分析通过Matlab最优化软件以及LMI工具箱协助完成.

（1）样本数据采集

从深圳证券交易市场选取5只股票，股票代码分别为000565，000878，000638，000926，000043.实证样本原始数据来源于益盟操盘手2012年11月12日至2012年12月21日的日开、收盘价格.根据样本数据可以得出每只股票的日收益率，见表1.

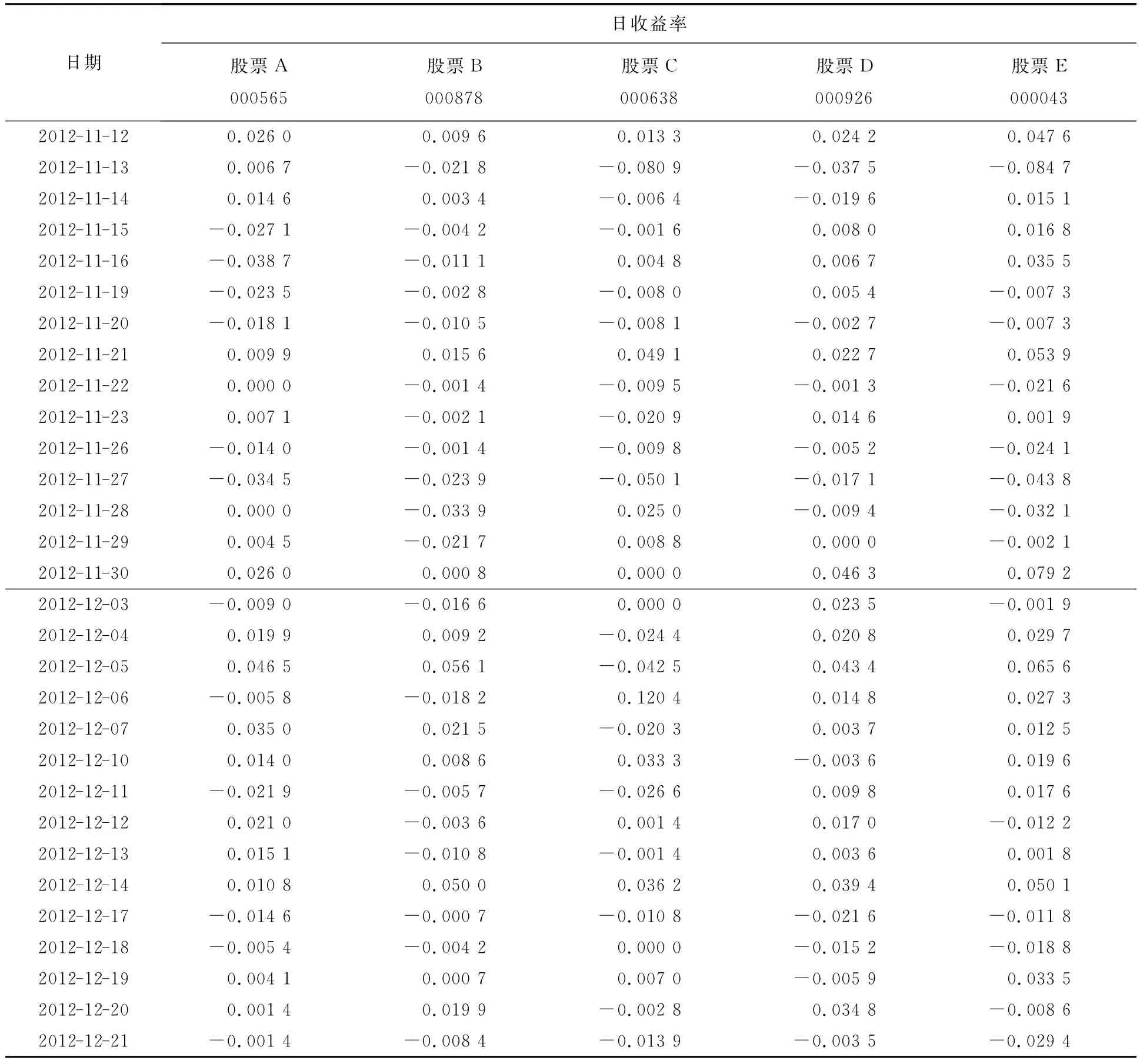
表1 股票日收益率

（2）交易费用函数

根据模型（1），交易费用函数可以取为

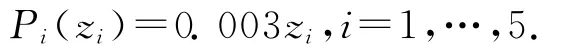
（3）基准投资组合

取基准投资组合权重为

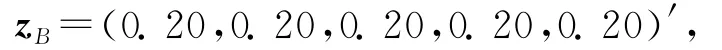
则考虑交易费用后的基准投资组合权重为

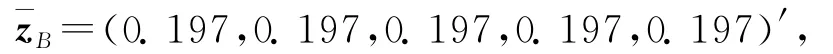
收益为¯βB＝0.002 7.

（4）有效边界组合

我们将30个交易日收益率的算术平均值取为

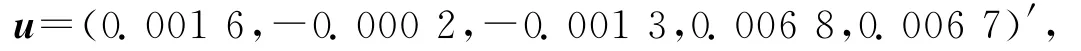
并利用这30个交易日的收益率得到

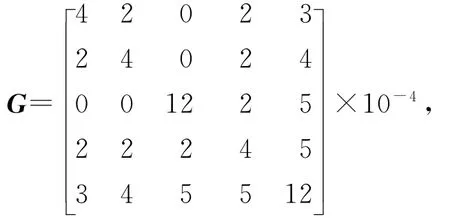
根据模型（3）得到有效边界组合权重

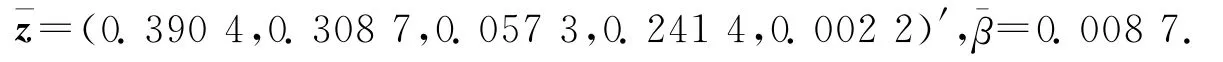
（5）鲁棒投资组合策略

首先考虑t＝2（k＝1，2）的情形，表明分别由两个协方差矩阵（G1，G2）和两个期望收益向量（u1，u2）组成不确定性情景集.在这里，G1，u1和前述的G和u的算法相同.然后通过蒙特卡洛模拟法模拟10 000次得到u2＝（0.004 4，0.01），根据所给的前15个交易日收益率向量的协方差矩阵以及后15个交易日收益率向量的协方差矩阵分别按0.3，0.7的权重加权得到

设定跟踪误差的最大波动α1＝0.001 4，α2＝0.001 6，则通过模型（4）得到的权重及最优解为¯zl＝（0.250 7，0.128 5，0.301 8，0.134 3，0.184 7）′，¯βL＝0.015 3.

根据上述数据结果可知，通过鲁棒策略我们不仅得到了最优解，而且求解出较基准组合和有效边界组合更为理想的权重分配，在鲁棒策略对投资组合进行优化的过程当中，我们除了利用多种情景集来表述未来协方差和期望收益的不确定性，在投资组合多次调整的情况下依然能够保持较高的收益率外，同时也可以避免因协方差和期望收益的估计值不准确所导致的计算结果偏离所要的最优值，因此，鲁棒策略会尽可能地减少投资管理者在运作当中所转换的成本.

4 结论

现今风险资产交易市场，股票的期望收益和协方差矩阵都具有不确定性，本文利用鲁棒策略确定多个情景集使得投资组合权重的选择更加合理，以实现投资管理者的收益最大化，并添加交易费用于模型当中，这使得模型更加贴近于大额投资情况下金融市场的实际交易，最后运用LMI验证了附加交易费用的动态投资组合鲁棒策略的有效性.鲁棒优化模型的建立使得投资组合的理论得到了相应的扩展和完善，并且更加符合现实的市场交易，在投资选择的实物当中具有非常广泛的应用价值.

［1］ MARKOWITZ H M.Portfolio selection［J］.Journal of Finance，1952，7：77－91.

［2］ LOBO VANDENBERGHE L，BOYD S，LEBERT H.Second－order cone programming：interior－point methods and engineering applications［J］.Linear Algebra Application，1998，284：193－228.

［3］ PINARA M C，TUTUNCU R H.Robust profit opportunities in risky financial portfolios［J］.Operations Research Letters，2005，33：331－340.

［4］ BEN－TAL A，NEMIROVSKI A.Robust convex optimization［J］.Mathematics of Operations Research，1998，23：769－805.

［5］ GOLDFARB D，IYENGAR G.Robust portfolio selection problems［J］.Mathematics of Operations Research，2003：97：1－38.

［6］ BEN A.，NEMIROVSKI A.Robust optimization－methodology and applications［J］.Mathematics Program，2002，92：889－909.

［7］ CHEN W，TAN S H.Robust portfolio selection based on asymmetric measures of variability of stock returns［J］.Journal of Computational and Applied Mathematics，2009，232：295－304.

［8］ FABOZZI F J，PETR N K，DESSISLAVA A P，et al.Robust portfolio optimization［J］.The Journal of Portfolio Management，2007：40－48.

［9］ ROLL R.A mean－variance analysis of tracking error［J］.Journal of Portfolio Management，1992，18：13－22.

［10］ SOYSTER A L.Convex programming with set inclusive constraints and applications to inexact linear programming［J］.Operations Research，1973，21：1154－1157.

［11］ COSTA O L V，PAIVA A C.Robust portfolio selection using linear－matrix inequalities［J］.Journal of Economic Dynamics and Control，2002，26：889－909.

［12］ LU ZHAOSONG.Robust portfolio selection based on a joint ellipsoidal uncertainty set［J］.Optimization Methods and Software，2011，26：89－104.

［13］ BERTSIMAS D，PACHAMANOVA D.Robust multiperiod portfolio management in the presence of transaction costs［J］.Computers and Operations Research，2008，35：3－17.

［14］ ERDOGANY E，GOLDFARB D，IYENGAR G.Robust active portfolio management［R］.Department of Industrial Engineering and Operations Research，Columbia University，USA，CORC Technical Report TR－2004－11，Nov.2006.

［15］ HONG－GANG XUE，CHENG－XIAN XU，ZONG－XIAN FENG.Mean－variance portfolio optimal problem under concave transaction cost［J］.Applied Mathematics and Computation，2006，174：1－12.

Robust strategy of dynamic portfolio with transaction cost

ZHENG Dong，LIANG Xi－kun
（Hangzhou Institute of Service Engineering，Hangzhou Normal University，Hangzhou 310036，China）

Based on the uncertainty of expected return and covariant matrix of risk assets，the robust strategy for dynamic portfolio with transaction costs is discussed in this paper.The result of empirical analysis by using LMI method was compared with the one of benchmark portfolio and the one of efficient frontier portfolio respectively.As far as the distribution of weights，the robust strategy of dynamic portfolio with transaction costs is more reasonable and the final returns are also better than other models.It is concluded that the models with transaction costs are closer to the actual transaction of financial markets in the condition of large investment.

mean－variance model；portfolio optimization；tracking error；robust；transaction cost

O 221 ［学科代码］ 110·74

A

（责任编辑：陶 理）

1000－1832（2014）02－0030－05

10.11672／dbsdzk2014－02－007

2013－03－16

国家自然科学基金资助项目（10971162）；浙江省自然科学基金资助项目（Y6110178）；杭州师范大学研究基金资助项目.

郑冬（1988—），男，硕士研究生，主要从事金融工程与金融计算研究；梁锡坤（1968—），男，博士，副教授，主要从事金融工程与金融计算，算法设计与分析，智能信息处理研究.