基于全量补偿算法的结构损伤识别

王凤刚，凌贤长，2，徐训，张锋，赵莹莹

（1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090；2.中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室，甘肃兰州730000）

基于全量补偿算法的结构损伤识别

王凤刚1，凌贤长1，2，徐训1，张锋1，赵莹莹1

（1.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090；2.中国科学院寒区旱区环境与工程研究所冻土工程国家重点实验室，甘肃兰州730000）

频率和振型是反应结构动力特性的主要模态参数，文中对损伤结构的频率和振型进行了研究。通过实测损伤结构的频率和振型，利用矩阵理论修正理论有限元模型，使之与实测损伤结构的频率和振型一致；将修正的理论有限元模型表达成单元刚度矩阵与损伤因子的线性组合，把损伤识别问题转化为组合系数的识别问题。给定损伤因子的合理取值范围，用优化方法求解损伤因子。通过对十跨桁架结构的数值仿真，仅用结构的前5阶频率和振型就能很好的识别结构的损伤，且该方法不需要对实测振型进行归一化处理，具有较强的实用性。

补偿算法；损伤识别；频率；振型；模态参数；损伤因子；归一化

土木工程结构随着服役时间的增加、材料性能的退化及环境荷载的改变，导致结构失效的可能性越来越大。为保证结构安全，减少经济损失，在20世纪70年代就开展了结构损伤诊断技术的研究工作［1］。结构损伤识别是找出结构损伤并给出损伤程度及位置［2］，为后续评估结构安全提供依据，是健康监测技术的关键。由于结构振动信息易于提取，且结构振动特性反应的是结构全局信息，因此，基于振动信号的结构损伤识别得到广泛研究。

基于振动特性的系统损伤识别可分为无反演方法和反演方法。无反演方法一般是通过频率、振型及其衍生量的动力指纹［3-5］来判断结构有无损伤。文献［6］利用模态曲率的改变率，对500 kV输电塔的损伤进行了识别。单元模态应变能损伤指标对开裂损伤和支座损伤有较好的识别效果［7］。杨栋等［8］定义了递归矩阵奇异值熵作为结构的损伤特征指标。这一类方法难以进行损伤定位及损伤程度的确定。反演方法一般是通过优化［9-10］或智能算法［11-13］等方法对结构损伤进行判定，定位及损伤程度确定。结构监测只能监测部分测点，随机损伤定位向量法对桁架桥梁［14］和钢框架结构［15］有较好的识别效果。针对对称结构、对称损伤识别不准的问题，文献［16］提出了移动附加质量的方法来改变结构的对称性。对于大型复杂结构，测量信息严重不足，导致对结构损伤识别的结果不可靠，侯吉林等［17］提出了局部主频率子结构损伤识别方法。结构模型和测量响应均存在噪声，噪声的存在使结构损伤识别存在数值不稳定现象，Tikhonov正则化方法是改善矩阵病态常用的方法，文献［18］通过在Tikhonov罚函数中引入光滑函数的方法，改善了噪声对结构损伤的影响。用概率的方法来研究噪声对结构损伤识别的影响是一种有效的方法。文献［19］提出了基于Bayesian理论的信息融合技术来提高结构损伤识别结果的准确性。

频率和振型是结构的模态参数，能反应结构的动力学特性，是一种全局变量。本文利用损伤结构的部分频率和振型信息，发展了一种基于优化的损伤识别反演算法。

1 全量补偿算法理论分析

1.1 结构特征方程

理论有限元模型的无阻尼自由振动特征方程为

式中：M为结构质量矩阵，K为结构刚度矩阵，Φ＝[φ1，…，φi，…，φN]为结构的振型矩阵，Λ＝diag(，…，，…，)为结构的频率平方组成的对角阵。令

则式（1）可写为

1.2 理论有限元模型的频率修正

结构损伤后，结构频率发生变化，通过修正理论有限元模型，使得修正后的理论有限元模型的频率值和损伤结构的频率值相同。将式（3）写成分量形式并做等价变形有：

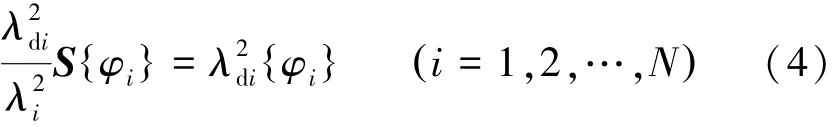
式中：λdi为损伤结构的频率。

将式（4）写成矩阵形式有

式中：Λd＝diag(，…，…，)，是由损伤模型的频率的平方组成的对角阵。

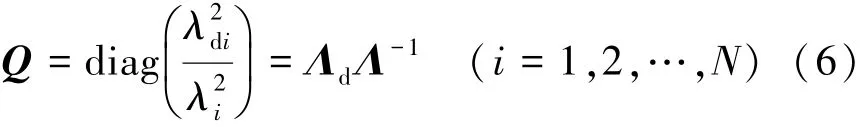
若仅已知一部分损伤结构频率，假定为n阶频率，则用损伤结构的n阶频率替换理论模型的n阶频率，即

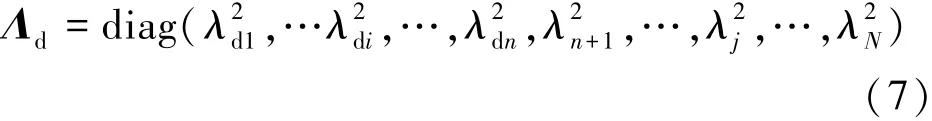
式中：λj为理论模型的频率。令L＝SQ。则式（5）可表示为

式（8）是通过频率对理论有限元模型的第一次修正，此时理论有限元模型已有n阶频率和实测损伤结构的n阶频率相等。

1.3 理论有限元模型的振型修正

在用频率修正理论有限元模型的基础上，再次通过振型修正理论有限元模型，使其有n阶振型和实测损伤结构已知的n阶振型相等。

根据矩阵理论，相似矩阵有相同的特征值。假设L和R是相似矩阵，即存在一个N×N阶的可逆矩阵P，使L和R满足：

下面构造N×N阶的可逆矩阵P。对式（8）进行等价变形有

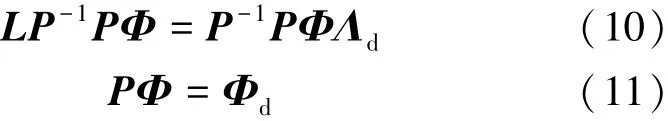
式中：Φd＝[φd1，…，φdi，…，φdN]是损伤模型的振型矩阵，φdi表示损伤模型的第i阶振型。

式（10）左右两边同时乘以P，将式（11）入式（10）有

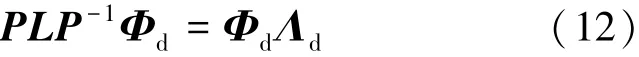
式（9）代入式（12）有：

式中：损伤结构振型矩阵Φd仅已知一部分振型，Φd中未知振型用理论模型的振型矩阵Φ中对应振型替代，即

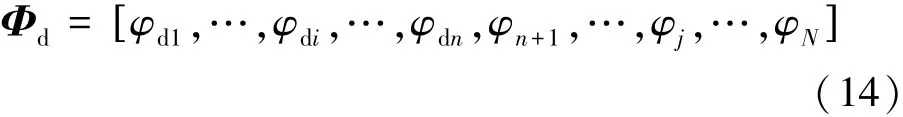
式中：φj表示理论模型的第j阶振型。由式（13）可求得通过频率和振型修正的系统矩阵R：

由式（15）可知，用损伤结构不做归一化处理的实测振型修正理论有限元模型的振型，与用损伤结构归一化处理的实测振型修正理论有限元模型的结果一致，说明对损伤结构实测振型不做归一化处理，对理论有限元模型的修正无影响。在对损伤结构振型的测试过程中，得到的振型往往不是归一化的振型，上述对理论有限元模型振型的修正不要求振型归一化，为对实测数据的处理带来很大方便。

1.4 刚度矩阵对称性修正

通过对理论有限元模型的频率修正和振型修正，使修正后的结构R有n阶频率和振型与损伤结构的实测n阶频率和振型精确相等。修正后结构的频率为Λd，振型为Φd。若假定实际结构质量矩阵和理论有限元分析一致，则对理论有限元模型修正后结构的刚度矩阵为

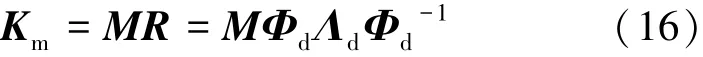
Km为结构的整体刚度矩阵，必须满足对称性的要求，令

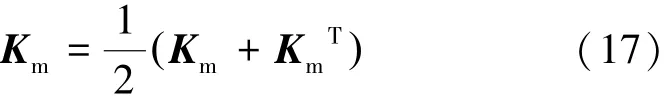
1.5 构造优化目标函数

结构整体刚度矩阵由单元刚度矩阵线性组合。α＝(α1，…，αi，…，αN)为组合系数。αi的取值在[01]。当αi＝0，表示第i个单元完全损伤；当αi＝1，表示第i个单元完好。为了求解组合系数α，构造优化函数，使式（17）的Km与损伤结构刚度矩阵真值Kd的差值的Frobenius范数最小。损伤结构的刚度矩阵Kd可表示为

令ε为Km和Kd之间的误差函数，以误差函数ε达到最小建立目标函数：

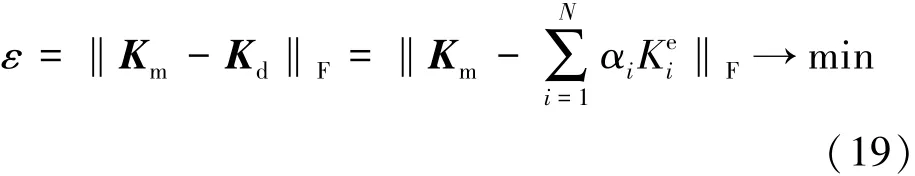
约束条件为

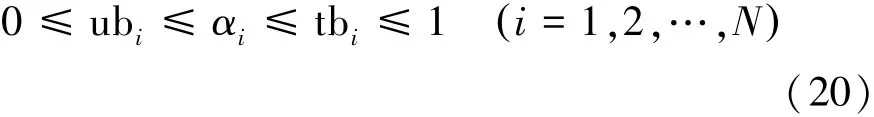
ubi和tbi为αi的上下界限值，若能大概估计单元刚度矩阵的变化范围，则对αi的搜索范围变小，减小计算量，对识别结果的精度也有提高。

1.6 算法终止条件

设α＝(α1，…，αi，…，αN)为满足式（19）和式（20）的解，若下式成立：

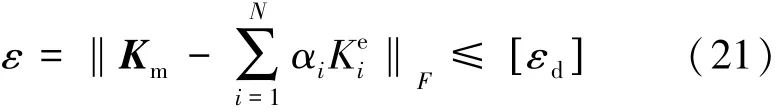
式中：εd[]为误差限值。由式（21）有

式中：为损伤结构刚度矩阵Kd的一个最优估计。若式（21）不成立，则令

将式（23）计算出来的K代回式（1）重新计算Φ和Λ，直至式（21）满足或达到预设的循环次数退出迭代。以迭代循环次数中min(ε)对应的α＝(α1，…，αi，…，αN)值作为损伤结构刚度矩阵的最优识别值，识别的损伤结构刚度矩阵用式（22）计算。

2 数值仿真

为验证上述算法的有效性，建立了一个十跨平面桁架的数值模型（图1）。图1中节点处数字表示节点编号，共20个节点；括号中数字表示桁架杆件单元编号，共37根杆件单元。该平面桁架结构有36个自由度。表1给出了平面桁架结构杆件的线刚度、线密度及单元杆件与x轴的夹角。

图1 平面桁架结构计算模型Fig.1 The calculation model of plane truss structure

桁架结构单元损伤通过折减单元线刚度来模拟，假定所有杆件均有不同程度的损伤，单元损伤参数如表2所示。通过测量结构响应，用随机子空间［20］方法获取损伤结构前5阶频率及振型，频率如表3所示，图2为损伤结构振型。算法误差限值[εd]设为1，最大循环次数为500次，通过误差限值[εd]和最大循环次数避免程序陷入死循环。若程序是由循环次数控制退出循环，在500次循环中，找出误差值ε最小时对应的识别刚度作为最终识别值。

在表2的损伤工况下，结构频率变化能达到10%左右，说明频率对结构损伤较为敏感。图2给出了完好结构和损伤结构的前5阶振型，从图中可以看出，振型的变化率没有频率变化率明显。表4给出了损伤结构线刚度真值和识别值。从表4中可以看出，最大识别误差不超过3%。

表1 桁架结构材料参数和几何参数Table 1 Material and geometrical properties of the truss

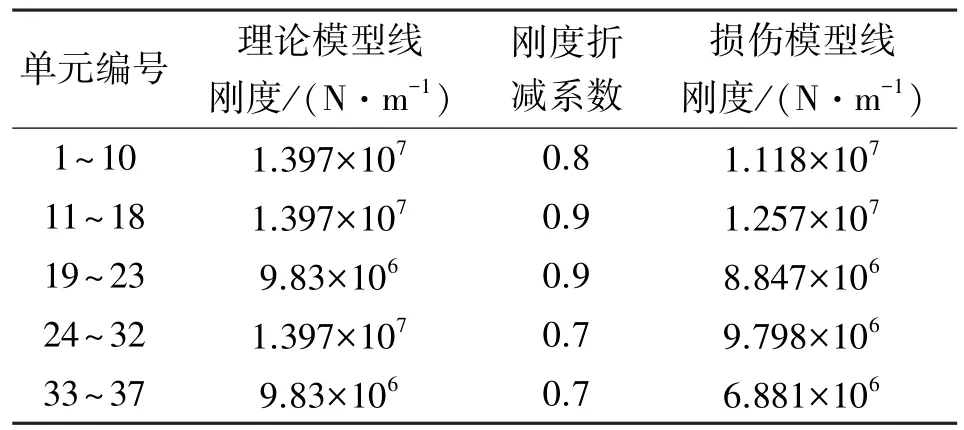
表2 结构损伤工况Table 2 Damage case of the truss

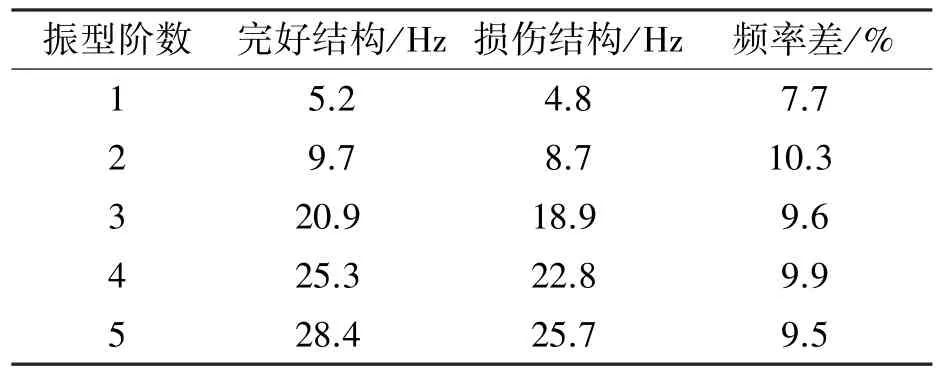
表3 结构自振频率Table 3 The frequency of the truss

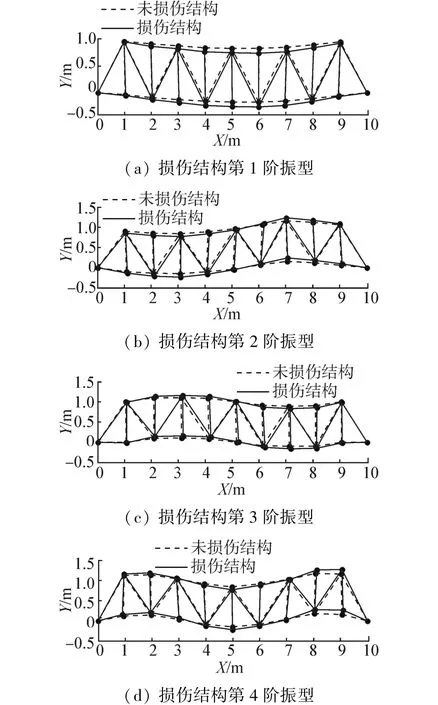
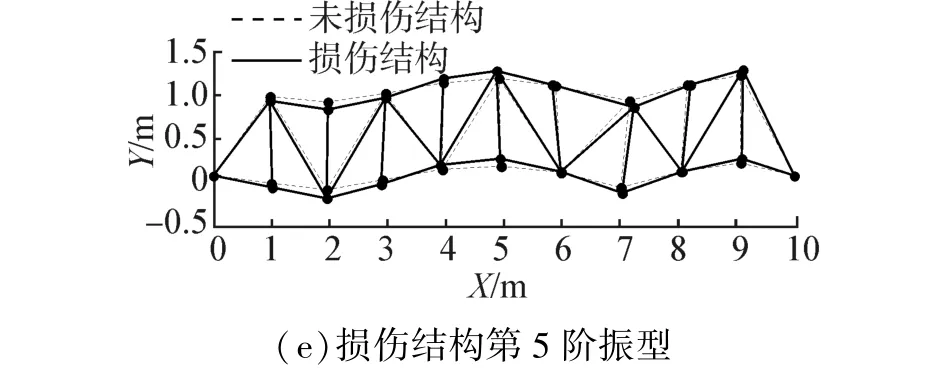
图2 损伤结构模态振型Fig.2 The mode shape of the damaged structure

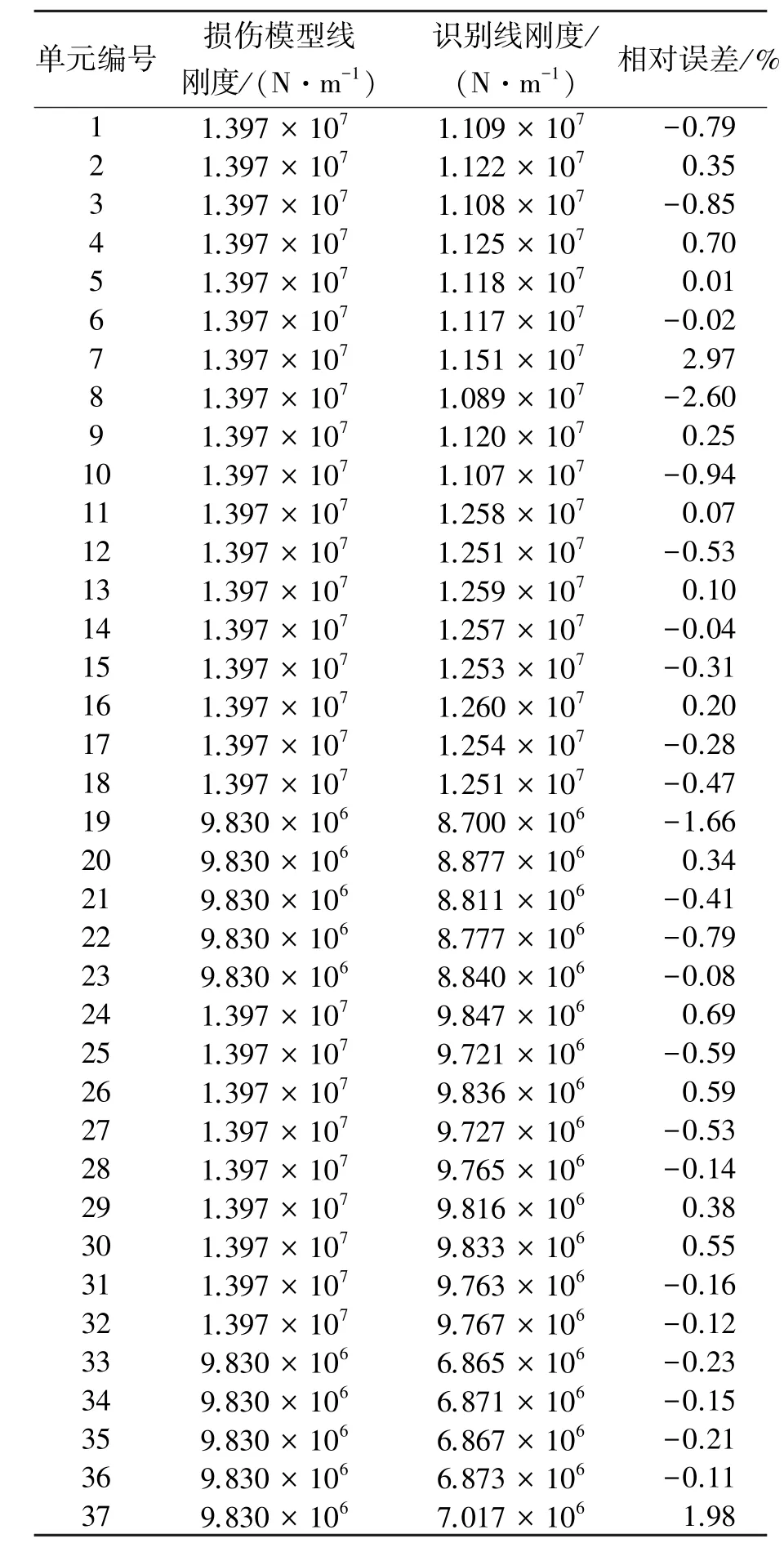
表4 损伤结构线刚度真值及识别值Table 4 True value and identification value of damaged structure linear stiffness

3 结论

本文提出了基于全量补偿的损伤识别方法，通过十跨桁架结构验证了算法的有效性，并得到如下主要结论：

1）振型对损伤的敏感程度比频率低，为保证结果的准确性，结构损伤达10%以上识别效果较好；

2）数值仿真假定了结构所有杆件均有不同程度的损伤，识别的最大误差不超过3%，表明算法对损伤杆件数目无限制；

3）对频率和振型的修正采用的是矩阵理论中构造特征值和特征向量的方法修正，在这过程中无误差引入，因此，即使频率和振型对损伤不太敏感也能取得较好的识别效果；

4）数值仿真仅利用了结构的前5阶频率和振型，对于实际问题，结构的前几阶频率和振型比较容易获取，且前几阶频率和振型比较准确；

5）算法对振型不要求归一化处理，对于实际问题很难对振型进行归一化处理，因此，该方法具有较强的实际操作性。

［1］CAWLEY P，ADAMS R D.The location of defects in structures from measurements of the natural frequencies［J］.Journal of Strain Analysis，1979，14（2）：49-57.

［2］KIM H，MELHEM H.Damage detection of structures by wavelet analysis［J］.Journal of Engineering Structures，2004，26（3）：7-14.

［3］SALAWU O S.Detection of structural damage through changes in frequency：a review［J］.Engineering Structures，1997，19（9）：718-723.

［4］VESTRONI F，CAPECCHI D.Damage detection in beam structures based on frequency measurements［J］.Journal of Engineering Mechanics，2000，126（7）：761-768.

［5］李范春，李成.结构损伤识别的数值模拟［J］.船舶力学，2006，10（5）：119-126.LI Fanchun，LI Cheng.Numerical simulation of the structural damage identification［J］.Journal of Ship Mechanics.2006，10（5）：119-126.

［6］刘春城，刘佼，李宏男.基于支持向量机的大型输电铁塔损伤识别方法研究［J］.应用基础与工程科学学报，2010，18（4）：616-625.LIU Chuncheng，LIU Jiao，LI Hongnan.Damage identification for transmission tower based on support vector machines［J］.Journal of Basic Science and Engineering，2010，18（4）：616-625.

［7］宗周红，褚福鹏，牛杰.基于响应面模型修正的桥梁结构损伤识别方法［J］.土木工程学报，2013，46（2）：115-122.ZONG Zhouhong，CHU Fupeng，NIU Jie.Damage identication methods of bridge structures using reponse surface based on finite element model updating［J］.China Civil Engineering Journal，2013，46（2）：115-122.

［8］杨栋，任伟新.基于递归矩阵奇异熵的损伤识别方法［J］.振动与冲击，2012，31（3）：60-63.YANG Dong，REN Weixin.Structure damage detecting using singular entropy of recurrence matrix［J］.Journal of Vibration and Shock，2012，31（3）：60-63.

［9］杜思义，殷学纲，陈淮.基于矩阵摄动理论识别结构损伤的筛选法［J］.应用力学学报，2008，25（1）：75-78.DU Siyi，YIN Xuegang，CHEN Huai.Sieve method for identifying damage based on matrix perturbation theory［J］.Chinese Journal of Applied Mechanics，2008，25（1）：75-78.

［10］REN W X，ROECK G.Structural damage identification using modal data.1：simulation verification［J］.Journal of Structural Engineering，2002，128（1）：87-95.

［11］ELKORDY M F，CHANG K C，LEE G C.Application of neural networks in vibrational signature analysis［J］.Journal of Engineering Mechanics，1998，120（2）：251-264.

［12］唐和生，薛松涛，陈镕，等.序贯最小二乘支持向量机的结构系统识别［J］.振动工程学报，2006，19（3）：382-387.TANG Hesheng，XUE Songtao，CHEN Rong，et al.Sequential LS-SVM for structural systems identification［J］.Journal of Vibration Engineering，2006，19（3）：382-387.

［13］孙继广.一类反特征值问题的最小二乘解［J］.计算数学，1987，9（2）：206-216.SUN Jiguang.Least-squares solutions of a class of inverse eigenvalue problems［J］.Mathematica Numerical Sinica，1987，9（2）：206-216.

［14］安永辉，欧进萍.大跨度钢桁桥模型的精细化损伤定位模拟和实验研究［J］.计算力学学报，2011，28（5）：730-736.AN Yonghui，OU Jinping.Experimental and numerical studied on precise damage localization of a long-span steel truss bridge model［J］.Chinese Journal of Computational Mechanics，2011，28（5）：730-736.

［15］王秋萍，郭迅.基于损伤部位向量法的钢框架损伤识别研究［J］.世界地震工程，2012，28（1）：50-55.WANG Qiuping，GUO Xun.DLV-based research on damage identification of steel frame［J］.World Earthquake Engineering，2012，28（1）：50-55.

［16］邓昌，顾培英，汤雷.基于移动附加质量的损伤诊断技术［J］.振动与冲击，2010，29（7）：135-138.DENG Chang，GU Peiying，Tang Lei.Damage diagnosis based on natural frequencies of a structure by adding known masses［J］.Journal of vibration and Shock，2010，29（7）：153-138.

［17］侯吉林，欧进萍，JANKOWSKI L.基于局部主频率的子结构损伤识别研究与实验［J］.工程力学，2012，29（9）：99-105.HOU Jilin，OU Jinping，JANKOWSKI L.The study and experiment of substructure damage identification based on local primary frequency［J］.Engineering Mechanics，2012，29（9）：99-105.

［18］张纯，宋固全，吴光宇.改进的正则化模型修正方法在结构损伤识别中的应用［J］.工程力学，2012，29（2）：29-43.ZHANG Chun，SONG Guquan，WU Guangyu.Structure damage identification by finite element model updated with improved tikhonov regularization［J］.Engineering Mechanics，2012，29（2）：29-43.

［19］孙晓丹，欧进萍，侯钢领，等.基于Bayesian估计的整体和局部信息融合的损伤识别［J］.工程力学，2012，29（6）：234-239.SUN Xiaodan，OU Jinping，HOU Gangling，et al.Damage Identification based on Baysian fusion of global and local information［J］.Engineering Mechanics，2012，29（6）：234-239.

［20］张笑华，任伟新，禹丹江.结构模态参数识别的随机子空间法［J］.福州大学学报，2005，33（10）：46-49.ZHANG Xiaohua，REN Weixin，YU Danjiang.Structural modal parameter identification appling stochastic subspace identification［J］.Journal of Fuzhou University，2005，33（10）：46-49.

Damage identification of a structure based on the total compensation method

WANG Fenggang1，LING Xianzhang1，2，XU Xun1，ZHANG Feng1，ZHAO Yingying1
（1.Civil Engineering Department，Harbin Institute of Technology，Harbin 150090，China；2.State Key Laboratory of Frozen Soil Engineering，Cold and Arid Regions Environmental and Engineering Research Institute，China Academy of Sciences，Lanzhou 730000，China）

The frequency and vibration mode were the main modal parameters representing dynamic characteristics of structure，and the frequency and vibration mode of the damaged structure were studied in this paper.First，through measuring the frequency and vibration modes of the damaged structure，a correction theory of matrix was used was used to modify the finite element model，which was consistent with the frequency and vibration modes measured from the damaged structure.Secondly，the finite element model（FEM）of the revision theory can be expressed by a linear combination of the element stiffness matrix and the damage factor.The damage identification problem transformed into the solution of the combination coefficients.Next，the range of reasonable values of damage factors was given and the damage factors could be solved by the optimization method.Through the numerical simulation of a ten-span truss structure，the structural damage could be identified significantly by merely using frequencies and vibration modes of the first five orders.Furthermore，the method does not need to normalize the measured vibration modes，but has strong applicability.

compensation method；damage identification；frequency；vibration mode；modal parameter；damage factor；normalization

10.3969／j.issn.1006-7043.201308018

http：／／www.cnki.net／kcms／detail／23.1390.U.20141204.1513.001.html

TU435；TU317

A

1006-7043（2014）12-1519-05

2013-08-09.网络出版时间：2014-12-04.

国家自然科学基金资助项目（51174261，51078111）.

王凤刚（1975-），男，博士研究生；凌贤长（1963-），男，教授，博士生导师.

王凤刚，E-mail：wang_fenggang＠163.com.