磁弹性理论中的守恒定律和路径无关积分

刘宗民，周健生，宋海燕

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001）

磁弹性理论中的守恒定律和路径无关积分

刘宗民，周健生，宋海燕

（哈尔滨工程大学航天与建筑工程学院，黑龙江哈尔滨150001）

守恒定律与路径无关积分是传统力学中的重要工具，在位错、断裂力学和其他缺陷理论中具有重要的应用价值。由于力场和磁场的共同作用，以及磁弹性材料本身的耦合性质，所以磁弹性体具有更为广泛的守恒定律和路径无关积分。文中通过定义4种不同的热力学函数，应用电磁场理论中的能量矩概念，建立了磁弹性理论中对偶形式的守恒定律，并由这些对偶形式的守恒定律得到了相应的路径无关积分。文中建立的守恒定律和路径无关积分，对研究磁弹性体中的缺陷理论将起到十分重要的作用。

磁弹性；能量矩；守恒定律；路径无关积分

守恒定律与路径无关积分是传统力学中的重要工具，在位错、断裂力学和其他缺陷理论中具有重要的应用价值。最有影响的路径无关积分是Rice的J积分［1］，Knowles和Sternberg的M积分［2］，以及Budiansky和Rice的L积分［3］。这些路径无关积分都和能量释放率相关［3-5］。利用势能与余能的对偶关系［6］，在文献［7-9］中给出了对偶形式的守恒定律和路径无关积分。

近年来，随着压电、压磁功能材料被广泛应用，守恒定律与路径无关积分的研究引起了广大学者的关注。这些守恒积分的主要优点就是可以描述奇异性的不变特性。进一步发展这些不变积分，使其能够用来表示其他物理场的奇异特性，如应力场和电磁场。压电材料受到力场和电场的共同作用，且压电材料本身的耦合性质，其能量泛函具有更为复杂的对偶形式［10］。王晓明运用循环积分以及能量矩的概念［11］，系统地建立了压电介质的守恒定律和相应的路径无关积分［12］。与电弹性材料类似，磁弹性材料受到力场和磁场的共同作用，可以建立与电弹性理论相同数量的守恒定律和路径无关积分。

在本文中，定义了4种不同的热力学函数，按照Eshelby提出的能量矩的概念，建立了磁弹性理论中的守恒定律和路径无关积分。这对于研究磁弹性体中的缺陷理论将起到十分重要的作用。

1 磁弹性理论的基本方程

设磁弹性体的体积为V，其边界为S，S＝Sσ＋Su＝SB＋Sψ，则磁弹性理论的基本方程如下［13-18］。

控制方程：

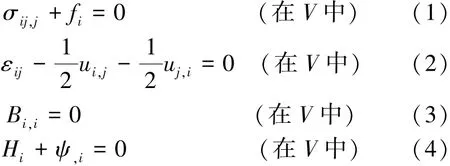
边界条件：

本构关系：

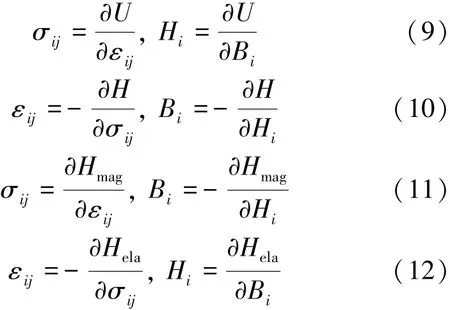
对于磁弹性体，内能U、焓H、磁焓Hmag、弹性焓Hela的表达式为

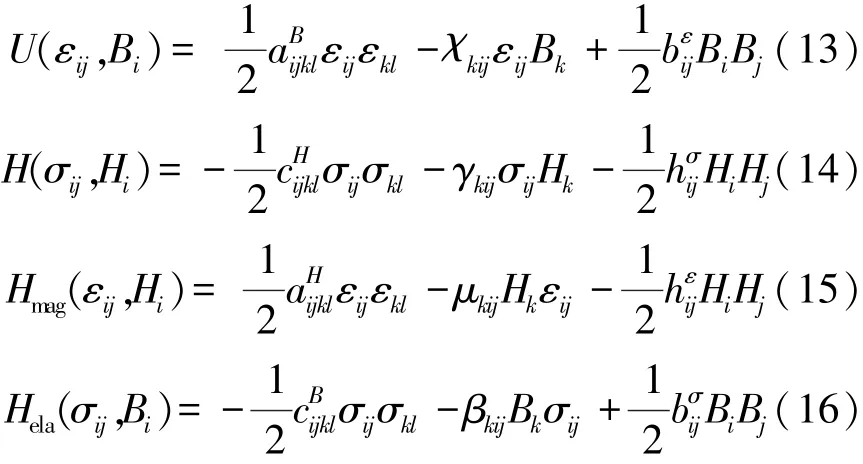
式中：σij为应力，fi为体积力，εij为应变，ui为位移，Bi、Hi和ψ分别为磁感应强度、磁场强度和磁势为表面力，ni为表面S的外法线方向余弦，为磁性系数，χkij、 γkij、μkij、βkij为压磁系数，“，”表示对空间坐标的偏导数，带有上划线的量为已知量。

2 守恒定律和路径无关积分

2.1 以内能表示的守恒定律和路径无关积分

设泛函Γ1为

考虑到式（2）和（3），可得

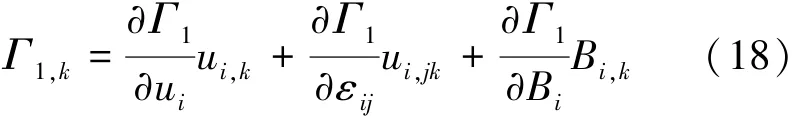
将本构关系式（9）代入式（18），可得

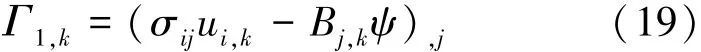
由式（19）可以得到关于内能的第一守恒定律的微分形式：

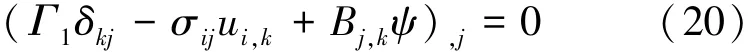
其积分形式为

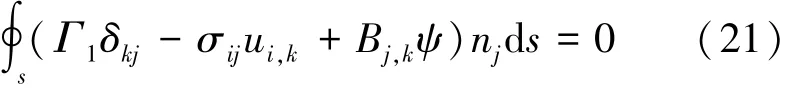
由于在上述推导中没有用到线性假设，即式（20）和（21）对非线性材料也适用。由式（20）和（21）可设定磁弹性体关于内能的能量矩为

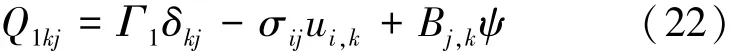
考虑到式（19）和（22），可得

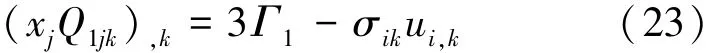
考虑到式（2）、（4）和（9），泛函Γ1可以进一步表示为

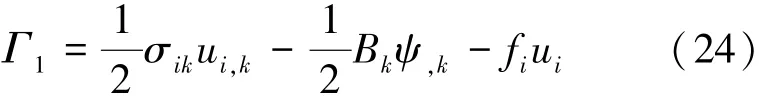
将式（24）代入式（23），并利用式（1）和（3），可得

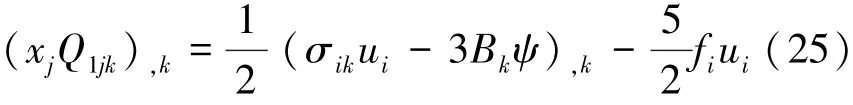
当fi＝0时，由式（25）可得到关于内能的第二守恒定律的微分形式：

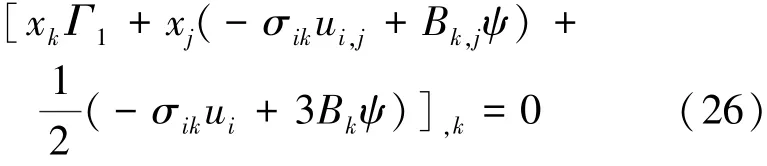
其积分形式为

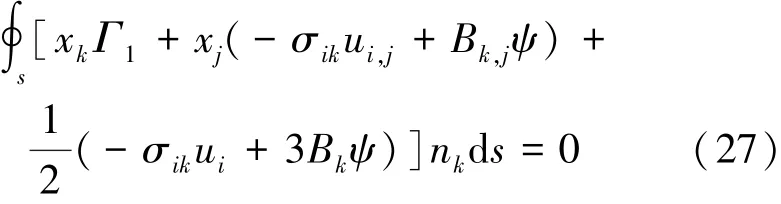
由式（21）和（27），可得到由内能表示的路径无关积分：

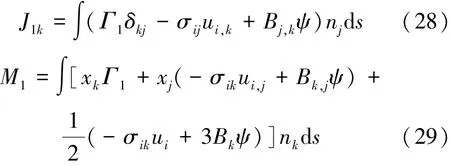
2.2 以焓表示的守恒定律和路径无关积分

设泛函Γ2为

考虑到式（1）和（4），可得

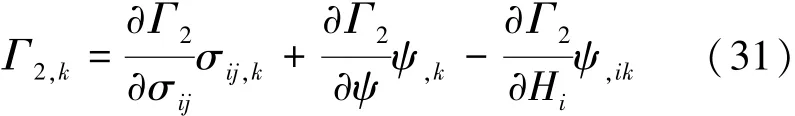
将本构关系式（10）代入式（31），可得

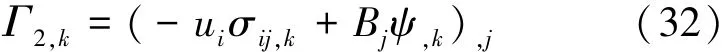
由式（32）可以得到关于焓的第一守恒定律的微分形式：

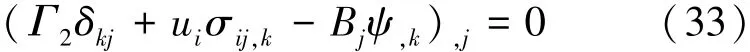
其积分形式为

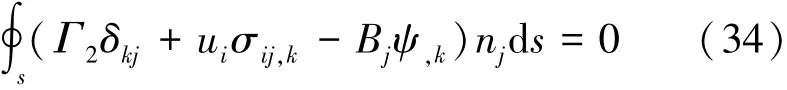
由于在上述推导中没有用到线性假设，即式（33）和式（34）对非线性材料也适用。由式（33）和式（34）可设定磁弹性体关于焓的能量矩为

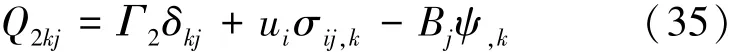
考虑到式（32）和（35），可得

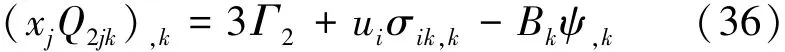
考虑到式（2）、式（4）和式（10），泛函Γ2可以进一步表示为

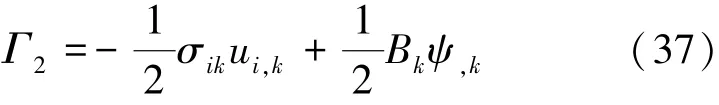
将式（37）代入式（36），并利用式（1）和式（3），可得

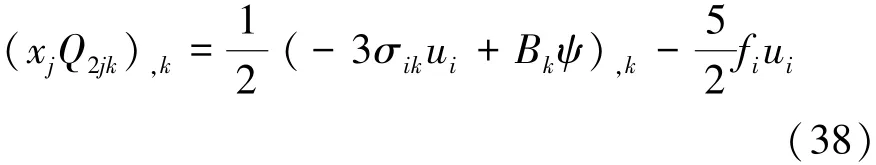
当fi＝0时，由式（38）可得到关于焓的第二守恒定律的微分形式：

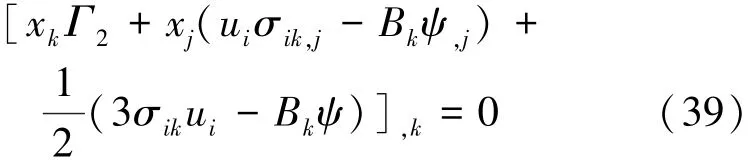
其积分形式为

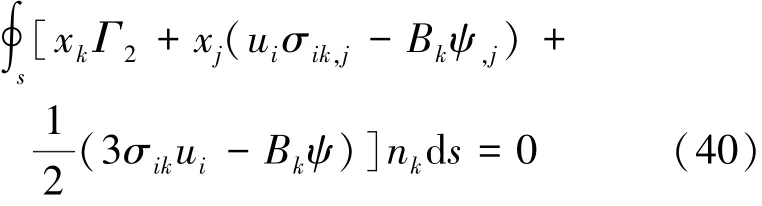
由式（34）和式（40），可得到由焓表示的路径无关积分：

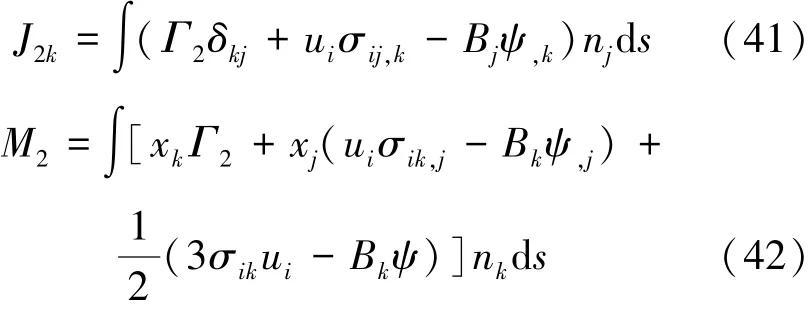
2.3 以磁焓表示的守恒定律和路径无关积分

设泛函Γ3为

考虑到式（2）和式（4），可得

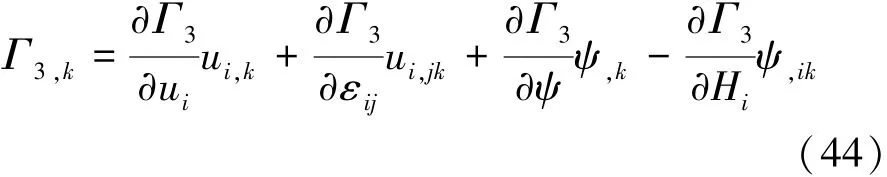
将本构关系式（11）代入式（44），可得

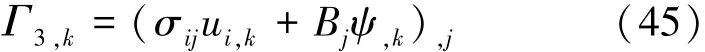
由式（45）可以得到关于磁焓的第一守恒定律的微分形式：

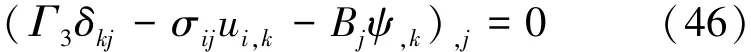
其积分形式为

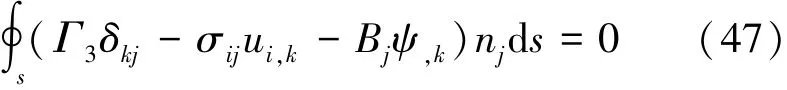
由于在上述推导中没有用到线性假设，即式（46）和式（47）对非线性材料也适用。由式（46）和式（47）可设定磁弹性体关于磁焓的能量矩为

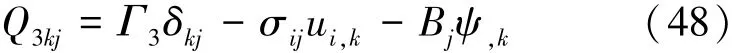
考虑到式（45）和式（48），可得

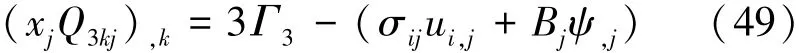
考虑到式（2）、式（4）和式（11），泛函Γ3可以进一步表示为

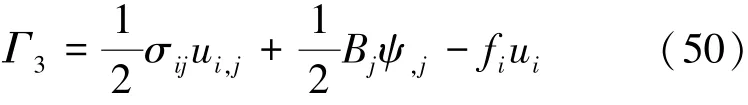
将式（50）代入式（49），并利用式（1）和式（3），可得

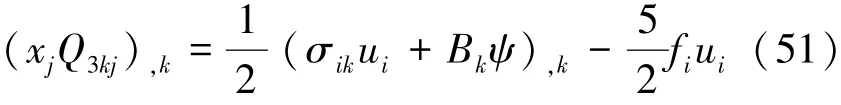
当fi＝0时，由式（48）和式（51）可得到关于磁焓的第二守恒定律的微分形式：

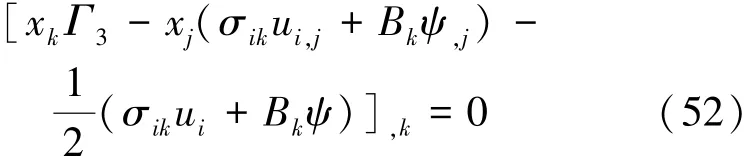
其积分形式为

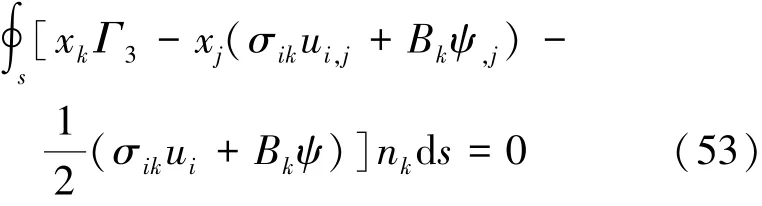
由式（47）和式（53），可得到由磁焓表示的路径无关积分：

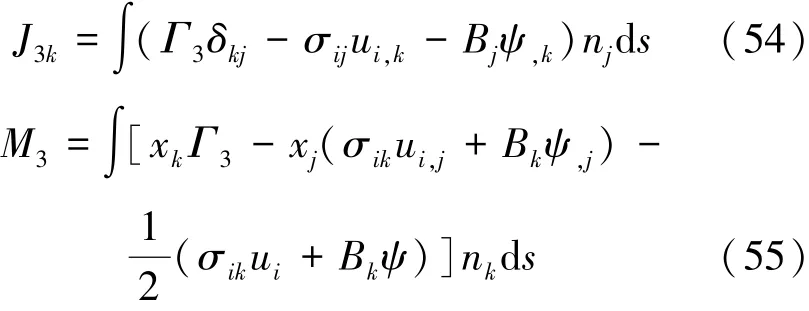
2.4 以弹性焓表示的守恒定律和路径无关积分

设泛函Γ4为

考虑到式（1）和式（3），可得

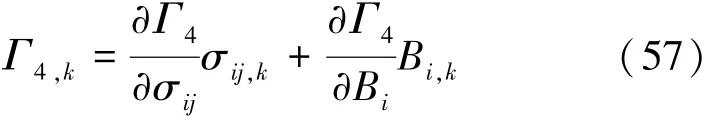
将本构关系式（12）代入式（57），可得

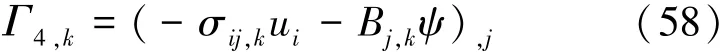
由式（58）可以得到关于弹性焓的第一守恒定律的微分形式

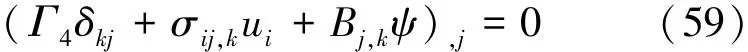
其积分形式为

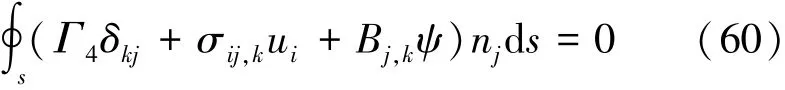
由于在上述推导中没有用到线性假设，即式（59）和式（60）对非线性材料也适用。由式（59）和式（60）可设定磁弹性体关于弹性焓的能量矩为

Q4kj＝Γ4δkj＋σij，kui＋Bj，kψ（61）

考虑到式（58）和式（61），可得

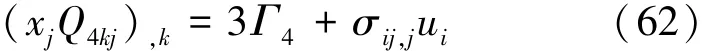
考虑到式（2）、式（4）和式（12），泛函Γ4可以进一步表示为

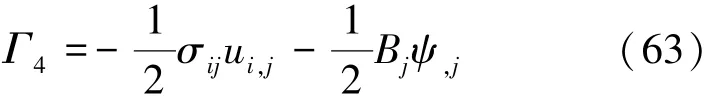
将式（63）代入式（62），并利用式（1）和式（3），可得

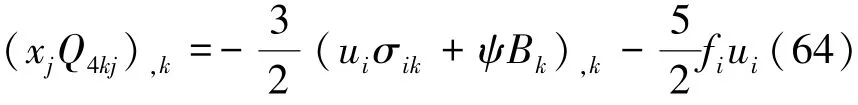
当fi＝0时，由式（61）和式（64）可得到关于弹性焓的第二守恒定律的微分形式：

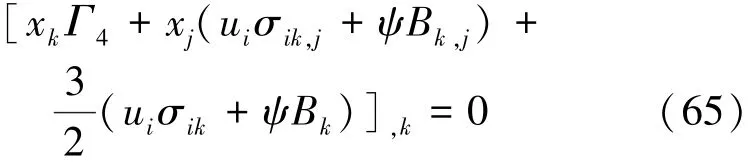
其积分形式为

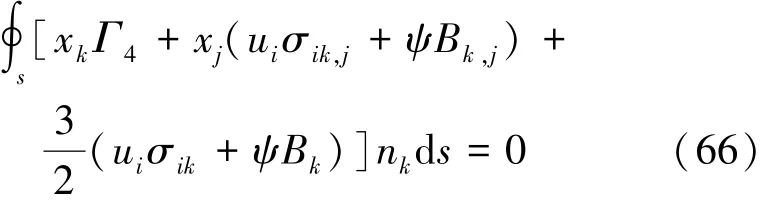
由式（60）和式（66），可得到由弹性焓表示的路径无关积分

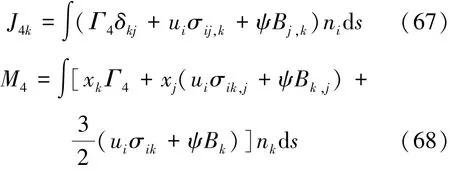
3 结论

由于力场和磁场的共同作用，以及磁弹性材料本身的耦合性质，所以磁弹性体具有更为广泛的守恒定律和路径无关积分。本文通过定义4种不同的热力学函数，建立了磁弹性体的守恒定律和相应的路径无关积分。

1）由于内能和焓的自变量互为共轭变量，所以由内能和焓分别表示的守恒定律互为对偶形式；由于磁焓与弹性焓的自变量互为共轭变量，所以由磁焓和弹性焓分别表示的守恒定律互为对偶形式。

2）采用Noether定理的方法也可以建立相同形式的守恒定律和路径无关积分，但采用能量矩的方法更为直接、简单且容易理解。

［1］RICE J R.A path independent integral and the approximate analysis of strain concentration by notches and cracks［J］.Journal of Applied Mechanics，1968，35（2）：379-386.

［2］KNOWLES J K，STERNBERG E.On a class of conservation laws in linearized and finite elastostatics［J］.Archives for Rational Mechanics Analysis，1972，44（3）：187-211.

［3］BUDIANSKY B，RICE J R.Conservation laws and energyrelease rates［J］.Journal of Applied Mechanics，1973，40（1）：201-203.

［4］CHEN Yiheng.Advances in conservation laws and energy release rates［M］.Dordrecht：Kluwer Academic Publishers，2002：261-296.

［5］SONG Haiyan，FAN Tao.Energy principle in crack propagation［J］.Key Engineering Materials，2012，488-489：593-596.

［6］宋海燕，梁立孚，周轶雷.一般力学广义变分原理的对偶形式［J］.哈尔滨工程大学学报，2004，25（6）：740-743，760.SONG Haiyan，LIANG Lifu，ZHOU Yilei.Dual form of generalized variational principles in general mechanics［J］.Journal of Harbin Engineering University，2004，25（6）：740-743，760.

［7］BUI H D.Dual path independent integrals in the boundaryvalue problems of cracks［J］.Engineering Fracture Mechanics，1974，6（2）：287-296.

［8］LI Xu.Dual conservation laws in elastostatics［J］.Engineering Fracture Mechanics，1988，29（2）：233-241.

［9］LIU Zongmin，MAO Jize，SONG Haiyan.J-integral and its dual form based on finite deformation theory［J］.Key Engineering Materials，2013，525-526：313-316.

［10］SONG Haiyan，LIU Zongmin，HUANG Yonghu.Dual form of generalized variational principles for piezoelectricity［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2013，14（3／4）：205-209.

［11］ESHELBY J D.The ealstic energy-momentum tensor［J］.Journal of Elasticity，1975，5（3／4）：321-335.

［12］王晓明，沈亚鹏.关于压电介质的守恒方程和路径无关积分［J］.力学学报，1995，27（1）：86-92.WANG Xiaoming，SHEN Yapeng.The conservation laws and path-independent integrals for piezoelectric media［J］.Acta Mechanica Sinica，1995，27（1）：86-92.

［13］MOON F C.Magneto-solid mechanics［M］.New York：John Wiley and Sons Inc，1984：53-86.

［14］梁立孚.力学和电磁学中的变分原理及其应用［M］.哈尔滨：哈尔滨工程大学出版社，2011：75-98.LIANG Lifu.Variational principles and applications in mechanics and electromagnetics［M］.Harbin：Harbin Engineering University Press，2011：75-98.

［15］SONG Haiyan，ZHOU Zhengong，LIANG Lifu，et al.Generalized variational principles of quasi-static electro-magneto-thermo-elasticity［J］.Key Engineering Materials，2010，419-420：153-156.

［16］宋海燕，李海波，梁立孚，等.准静态电磁热弹性体第二类H-R型广义变分原理［J］.强度与环境，2010，37（2）：8-16.SONG Haiyan，LI Haibo，LIANG Lifu，et al.The second H-R generalized variational principles of quasi-static electro-magneto-thermo-elasticity［J］.Structure and Environment Engineering，2010，37（2）：8-16.

［17］宋海燕，梁立孚，周振功.准静态电磁热弹性体余能原理和广义变分原理［J］.哈尔滨工程大学学报，2011，32（1）：33-37.SONG Haiyan，LIANG Lifu，ZHOU Zhengong.The complementary energy principle and generalized variational principles of quasi-static electro-magneto-thermo-elasticity［J］.Journal of Harbin Engineering University，2011，32（1）：33-37.

［18］Subcommittee on Magnetostrictive Materials of the Standards Activities Committee of the IEEE Ultrasonics，Ferroelectrics，and Frequency Control Society.IEEE standard on magnetostrictivematerials：piezomagneticnomenclature（IEEE Std 319-1990）［S］.New York：The Institute of E-lectrical and Electronics Engineers，1991.

Conservation laws and path-independent integrals in magnetoelasticity

LIU Zongmin，ZHOU Jiansheng，SONG Haiyan
（School of Aerospace and Civil Engineering，Harbin Engineering University，Harbin 150001，China）

Conservation laws and path-independent integrals are important tools in traditional mechanics，which have important applications in dislocation，fracture mechanics and defect theory.Due to the coupling action between stress field and magnetic field，and the coupling properties of magnetoelastic material，magnetoelasticity has more extensive conservation laws and path-independent integrals.By defining four different thermodynamic functions，and based on the concepts of energy-momentum tensor in electro-magnetic theory，the conservation laws and their dual forms in magnetoelasticity are established.The corresponding path-independent integrals in magnetoelasticity can be obtained.The conservation laws and path-independent integrals established in this paper could play an important role in studying defect theory in magnetoelasticity.

magnetoelasticity；energy-momentum；conservation laws；path-independent integrals

10.3969／j.issn.1006-7043.201309088

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201309088.html

TK124

A

1006-7043（2014）12-1503-04

2012-12-05.网络出版时间：2014-12-02.

国家自然科学基金资助项目（10272034）；中央高校基本科研业务费专项资金资助项目（HEUCF130205）；黑龙江省博士后科研启动金资助项目（LBH-Q11142）.

刘宗民（1976-），男，副教授，博士；宋海燕（1974-），女，副教授，博士.

宋海燕，E-mail：songhaiyan＠hrbeu.edu.cn.